基于Sqrt3细分算法的人体模型网格平滑∗

苏 刚 胡新荣 李佳黎 尹 汪 陈思园

（武汉纺织大学数学与计算机学院 武汉 430073）

1 引言

近年来，随着网络及虚拟现实技术的迅速发展，数字人体建模及动画模拟已经成为计算机图形学研究的热点方向之一。目前，数字人体建模技术主要分为五大类，分别是基于解剖学的数字人体建模、基于三维扫描数据的数字人体建模、基于图像序列的数字人体建模、三维软件（3DMax、Maya、Poser）人体建模以及参数化数字人体建模技术［1～2］。基于解剖学的数字人体建模技术采用了基于数字横断切片图像数据的几何建模方法，这类建模技术需要太多人工干预，建模效率低。基于三维扫描数据的数字人体建模采用结构光或激光三维扫描仪进行三维数字人体重建，利用该方法能重建与实际人体体型非常逼真的三维模型。但该方法的实现依赖于昂贵的设备，获取数据量大，重建速度慢，很难对数字人体模型进行控制和修改。基于图像序列的数字人体建模是利用从视频图像序列或照片序列中获取的二维图像来重建数字人体模型，这种方法花费较低，但对人体着装要求高，在获取三维人体模型精度和建模速度上难以达到平衡。通过三维建模软件绘制人体三维模型可以得到美观的人体模型，但建立模型成本较高，不适用于建立大量个性化的数字人体模型。

综上所述，我们采用的是参数化数字人体建模，该方法是基于传统几何建模方法上的一种更为抽象化的建模方法，通过几何约束来表达数字人体模型的形状特征，以抽象的特征参数表达真实人复杂的外部几何特征，依托于常规的几何建模方法，使设计人员能够在更高更抽象的层面进行人体设计［3］。由该方法建立的人体模型是由多边形面片组建的三维人体网格模型，虽然具有规则的网格结构，与原始扫描人体获取数据相比，不仅大大减少了人体模型数据量，并能够极大地提高系统的计算效率，同时还保持了扫描人体的表面基本特征，但是表面不够光滑，没有真实人体圆润的感觉，不能满足实际应用的需要。因此，本文引用Sqrt3曲面细分算法［4～7］来实现三维人体模型的网格平滑。Sqrt3细分具备三角形面片增加缓慢，连续性自动保留等优点，并能在任意网格上达到C1连续。实验证明，利用该方法对三维人体模型进行光滑处理取得了很好的效果。

2 参数化数字人体建模

参数化数字人体建模是根据人体着装时服装与人体表面接触的特点和人体的整体结构特征，将人体模型分为肩部、躯干、上肢和下肢4个部分，每层有各自的数据结构和造型方法。它使得人体模型的曲面建模更加灵活，可以针对人体模型不同部位的几何特征，选择适合的曲面建模方法，而不必拘泥于某一种曲面表达方式。为建立个性化虚拟现实人体建模系统，满足不同用户的精度需求，本文提出了个性化人体模型重建方案，通过参数化数字人体建模思想和特征化建模方法，实现了个性化数字人体建模系统。如图1所示，用户通过该系统只需要修改形体参数的值，就可以使形体形状改变，实现个性化数字人体建模。通过参数化数字人体建模得到人体模型是由多边形面片组建的三维实体模型，虽然具有规则的网格结构，但是网格表面不够光滑，不能满足实际应用的要求，所以本文引用Sqrt3曲面细分法对人体网格模型进行光滑处理。

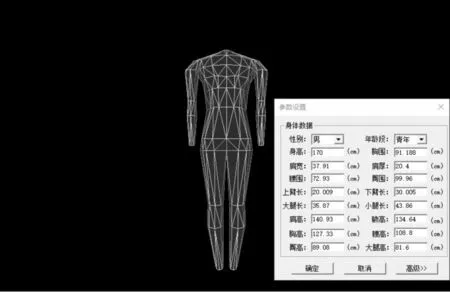
图1 个性化数字人体建模系统

3 Sqrt3细分曲面原理

细分曲面是用低分辨率的控制网格和定义在控制网格上的一种细分规则来表示光滑曲面的。目前，细分曲面方案有很多，典型的细分曲面方案有Loop细分法，改进Butterfly细分法，Sqrt3细分法、Catmull-Clark细分法、Doo-Sabin细分法以及基于GPU的PN-triangle 细分法等［8～12］。其中，Loop细分法，改进Butterfly细分法，Sqrt3细分法，PN-triangle细分法主要用来对三角网格进行网格平滑。从而结合我们建立的人体模型为三角网格模型，对这四种算法进行实验测试，来选择一种最合适的算法来对三维人体模型进行网格平滑处理。测试三维模型具有498个顶点，992个三角形面。测试数据如表1所示。通过参考文献［9］和表1实验数据可以了解到，Sqrt3细分法在面片的增长速度上和算法的逻辑复杂度之间达到了一种平衡，该细分算法简单高效，能缓解三角面片的增长速度，所以本文选择该曲面细分方案来对人体网格模型进行光滑处理。

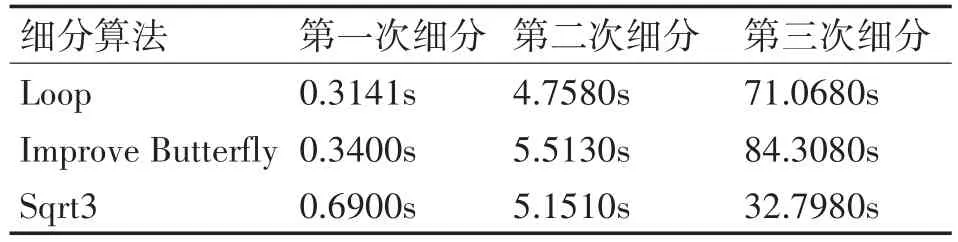
表1 曲面细分算法运行效率分析表

Sqrt3细分方案是由Kobbelt在2000年提出的一种逼近型、面分裂的三角网格细分方案，该细分曲面方案能有效缓解面片增长速度。Sqrt3采用一种全新的顶点插入和分裂方式，每次细分时，在每个三角形面插入一个新顶点，连接每个三角形面片的中心点和其顶点，然后去掉原三角形的内部边，这样使得三角形面的个数增加3倍，细分过程如图2所示。Sqrt3细分法使得三角形面片增加缓慢，不会出现尖锐三角形，并且连续性自动保留，适用于局部性适应性细分。

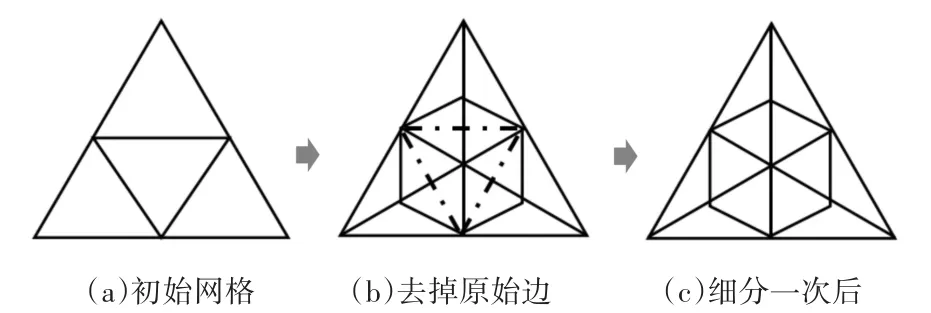
图2 Sqrt3细分过程

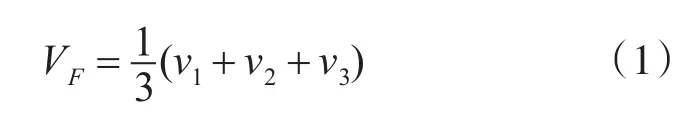
对于原始顶点，设新顶点（V-vertex）：顶点v相邻顶点为 v1，v2，v3，…，vn-1，则（V-vertex）新顶点 Vv

新面点（F-vertex）：设原始面片三角形的三个顶点为v1，v2，v3，新插入的中心点由下面的公式计算：由下面的公式计算：

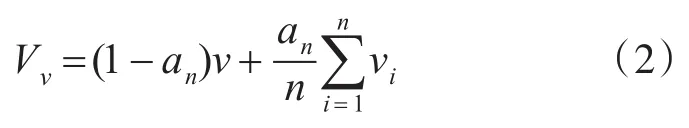
其中n为顶点个数，vi为其领域内的顶点，an的求解公式如下：

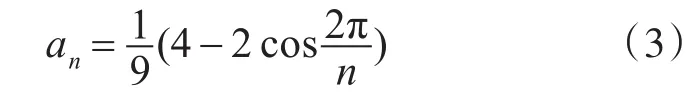
根据以上介绍，可以总结出Sqrt3细分法进行细分的步骤大致如下。

在大数据的背景下，教学环境也开始向信息化的方向发展。因此，对于高职院校而言，也应该积极地利用大数据的这一优势，建立相关的数学实验室，提高学生的数学实际操作能力。对于学生来说，信息化数学实验室的建立不仅能力吸引到他们的学习兴趣，也能够提高实际的数学学习效果，培养他们的数学应用能力。

Step1：逐个遍历三角形面片，通过面片求出每个面片对应的三个顶点，利用式（1）求出中心点的坐标，保存在面片的属性内；

Step2：把面片分为三个单独的面片，使中心点连接三角形面片的三个顶点；

Step3：把新产生的面片加入到新的面片序列中。

Step4：去除原始顶点的边；

Step5：对原始的顶点进行修正；

Step6：一次细分结束。

4 算法实现

4.1 设计数据结构

人体网格曲面的表示主要包括两个类：顶点类（CMyShape类）和三角形面类（CIndex类）。顶点类表示人体网格模型顶点数据的坐标值，人体网格模型中所有顶点都按顺序保存在动态数组CtypeP-trArray＜CobArray，CMyShape*＞m_Vertex中，三角形面类保存的是三角形三个顶点在m_Vertex动态数组中的索引号和细分曲面过程产生的边点索引。最后，所有三角形面都保存在动态数组CtypePtrArray＜CobArray，Cindex*＞m_Index中。

4.2 获得新顶点

v1为vertNew-＞x+=vert-＞x/3.0f，

v2为vertNew-＞x+=vert-＞x/3.0f，

v3为vertNew-＞x+=vert-＞x/3.0f，

即可以求出新插入的中心点的位置。按式（2），对原始顶点的改变Vv：

m_Vertex［（*v_iter）-＞index］-＞x*（1-alpha）+sum_x*（alpha/（float）vertexCounter）；

m_Vertex［（*v_iter）-＞index］-＞y*（1-alpha）+sum_y*（alpha/（float）vertexCounter）；

m_Vertex［（*v_iter）-＞index］-＞z*（1-alpha）+sum_z*（alpha/（float）vertexCounter）；

其中an按式（3）如下表示：

alpha=（4-2*cos（2*3.14159f/（float）vertexCounter））/9.0f

4.3 产生新三角形

按照细分规则，每次细分时，在每个三角形面插入一个新顶点，然后连接每个面片的中心点和原三角形的顶点，最后去掉原始网格的内部边。如图3所示，为人体网格模型局部细分过程图示，首先计算出每个三角面片的中心点，如图3（a）所示，设插入某一点P为某一个三角形的中心点，以点P所在三角形面片和该三角形相邻三角形的中心点形成的局部拓扑结构为例，新顶点与原三角形的三个顶点和相邻三角形面片的中心点相连得到图3（b）网格结构，然后去掉原三角形的内部边，经过一次细分得到图3（c）所示拓扑网格结构。

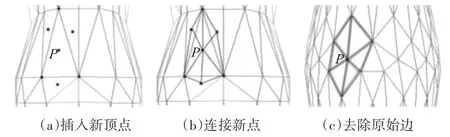
图3 新三角形产生过程

4.4 改变原顶点

如果三角形顶点的邻点已知的话，按式（2）很容易就可以求出移动后的新控制顶点，所以关键就在找到其邻点。搜索邻点时，遍历m_Index数组中所有CIndex对象，若三个顶点索引中有一个与该顶点索引相同，则另二个顶点索引所代表的顶点即为该顶点邻点。将新生成的点与相邻面生成的点连接，为所有新生成的点计算属性，最后去除重复顶点即可得到所有邻点。

5 结语

本文提出了一种针对参数化数字人体模型的基于Sqrt3细分的网格光滑方法，根据人体表面特征建立初始网格重建三维人体模型。通过Sqrt3细分规则对三维人体模型进行光滑处理。算法实现效果如图4所示。

为研究不同曲面细分算法对参数化三维人体建模人体模型光滑处理的性能，本文实现并验证了

参考文献［3］中王晖等用Loop细分法对人体模型进行光滑处理的算法，如图5所示，分别用一般三角形细分法、Loop细分法、Sqrt3细分法对人体模型光滑处理后得到一次细分和二次细分的效果图示。从人体模型表面光滑效果来看，一般三角形细分法增加了人体网格模型三角形面片的个数，但没有使人体模型达到光滑，仅仅是将人体网格模型的三角面片进行了细化，并增加了三角形和顶点的数量。Loop细分法和Sqrt3细分法对人体模型进行光滑处理已经有了明显的改善，人体模型在整体上实现了很好的光滑效果。其中，Loop曲面细分是一种基于三角网格的细分［13～15］，主要思想是在三角形点的每条边上插入新顶点，并将其两两相连，每次细分三角形个数将增加4倍。Loop曲面细分法可以达到C2连续，产生的曲面质量较高，但Loop细分对原有特征尤其尖锐特征的保持能力弱，产生的曲面具有较大的收缩性。Sqrt3细分算法可以达到C1连续，而且算法实现简单，速度快，提高了运行效率和分辨率。通过对比可以得出Loop细分法和Sqrt3细分法都会使人体网格模型会产生较大的收缩，特别是人体模型的四肢末端比较明显，这将是今后努力改进的方向。

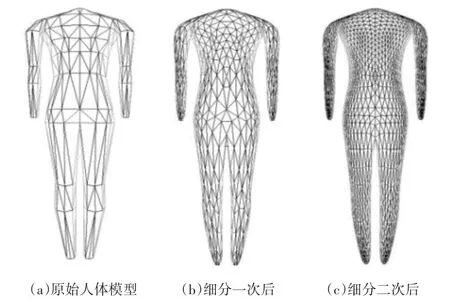
图4 细分曲面效果

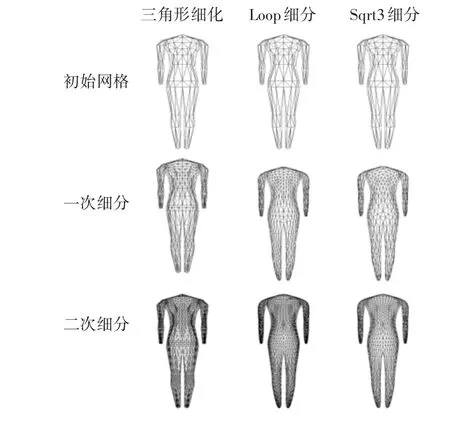
图5 细分算法曲面效果