基于模糊理论的图像增强算法研究∗
2019-03-26侯海啸
韩 涛 侯海啸
(中国飞行试验研究院 西安 710089)
1 引言
模糊理论是建立在模糊集概念上的。著名控制论专家、美国加州大学教授L.A扎德于l965年首先提出模糊集(Fuzzy set)的概念。奠定了模糊性数学处理的理论(简称模糊数学)的基础。复杂系统特别是有人干预的系统具有某种不确定性,模糊数学在处理这类常见系统时显得简捷与有力。在某种程度上弥补了经典数学与统计数学的不足。因此,迅速受到广泛重视。三十多年来,从理论到应用,从软技术到硬技术都取得丰硕成果,对相关领域和技术特别是一些高新技术的发展产生了日益显著的影响[1]。
本文主要阐述了图像增强的基本理论和模糊理论的基本知识,并把它们有机地结合起来,研究出一种全新的图像增强技术——模糊增强技术。模糊增强技术是模糊集合理论在数字图像处理中应用的产物。由于其以雄厚的数学为基础,这种方法较为严格并带有普遍性。由于计算较为灵活,不失为一种性价比较高的方法。实验表明,由于模糊增强技术利用灵活的选取模糊因子[2],改进处理效果,它比常用的直方图平坦化(Histogram Equalization)方法效果更好。如何利用模糊集合理论,开发数字图像处理新的工具,是我们正在研究的课题。可以预言,在不久的将来模糊集合的思想将会应用于数字图像处理的更多领域。
2 模糊特征隶属函数
模糊隶属函数的定义方式很多,大概分为11种,其中实际问题中最常用的隶属函数形式是所谓标准S型函数和π型函数。其中S型函数是一种从0到1的单调增长函数;π型函数是指中间高两边低的函数,它也可以用S型函数定义[3]。从图像处理的领域来看,转化成模糊域的灰度值是从低到高的连续过程,而且S型函数符合边缘的过渡变化过程,所以以S型函数作为模糊函数的基本变换形式很合理[4]。其实很多其他形式的模糊隶属函数形式都是由S型函数变换而来。S型函数格式如下:

然而S型函数在这里并不适合直接用作隶属函数。这里我们采用Pal和King所定义的隶属函数形式,根据灰度级阈值参数XT,而不是根据最大灰度级Xmax来定义新的隶属函数形式[5]。
定义新的隶属函数为
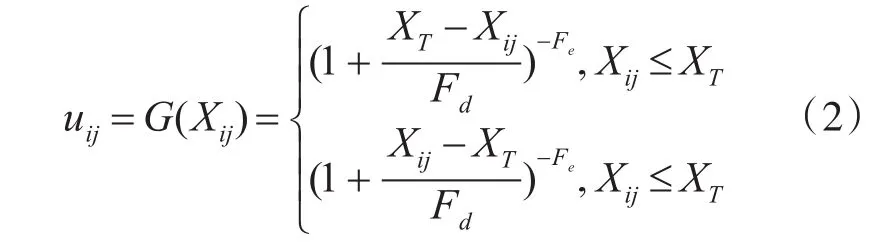
其中i=1,2,…,M;j=1,2,…,N。上式表明当Xij→ XT时,mij→ 1;当Xij值减小时,mij随之减小;Xij值增大时,mij随之增大。参数Fd称为倒数型模糊因子,Fe称作指数型模糊因子,他们均为正数,而且这些模糊因子取值将直接影响到模糊性的大小[6],即所取值决定了mij的曲线形状。在后面的软件测试中Fd可以由其他参数计算得出Fe,可根据图像内容的不同选取不同的值在实际工作中通常取2并且输入的空域图像在此经过G变换即得到与模糊特征平面相对应的矩阵[7]。
3 基于模糊集的图像增强方案
模糊增强方案的算法框图如图1所示。
3.1 对图像进行模糊增强
这种模糊增强就是在图像的模糊特征平面上对mij,进行非线性变换,其结果是增大(当mij>0.5)或者减小(当mij≤0.5)mij的值。本文选用如下增强算子[8]:
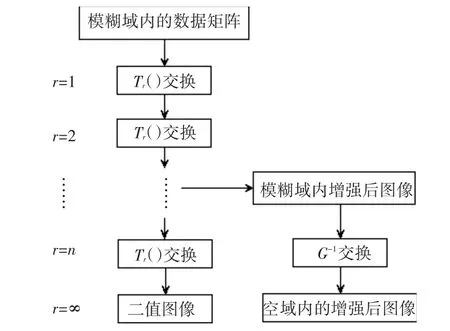
图1 模糊增强算法框图
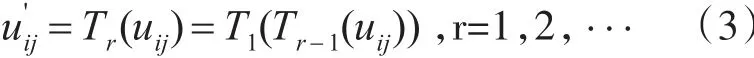
其中
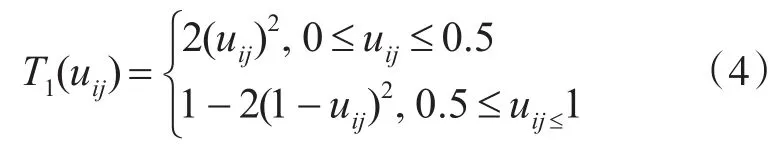
Tr可以定义为T1的多次递归调用。不难看出对Tr作有限次递归调用后图像可显著增强。随着迭代次数r的增大致使曲线越来越陡峭极限情况下,当r→∞时,Tr()将产生二值图像。图中箭头的方向指向r值增大时,曲线明显陡峭。
由此可见本文算法在低灰度区域和高灰度区域目标和背景分别进行模糊增强运算,即在低灰度区域主要进行衰减运算,从而使属于该区域的大部分像素的灰度值更低;而在高灰度区域则主要进行增强运算,从而使属于该地区的大部分像素的灰度值更高。
3.2 空域内的增强图像
从模糊域内的已增强的图像进行G-1逆变换,即得到已增强的空域图像。其逆变换G-1方式定义为
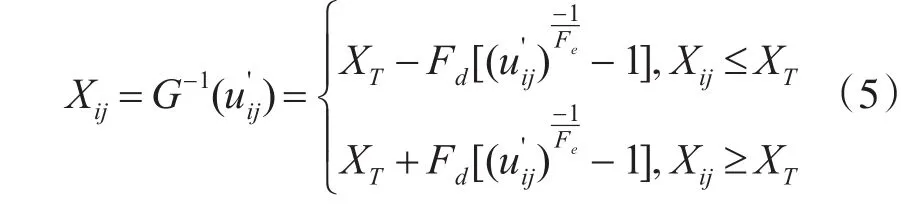
3.3 分块读入待增强的图像
通常情况下整幅图像包含了很复杂的背景信息目标信息,很难区别于背景信息。比如在图像增强的时候将整幅图像的直方图进行统计来区别低灰度和高灰度两部分,常常会漏掉重要的图像边缘信息。为解决这个问题本文方案采用叠进式窗口来处理,它有两处优点:
1)采用窗口式的分块处理,这样可以根据每一个图像中每一个区域的不同特点计算出每一块区域的阈值,即整幅图像不是只有一个阈值,而是每个分块子图有个阈值,这由根据图像的特点而分块的个数来决定的[9]。
2)采用重叠式窗口,可以避免在分块处理的时候漏掉某些重要的边缘信息。因为图像中某些灰度级在这个区域内得到增强,但被划到下一个区域内却没有得到增强。这样会影响到下一步的边缘检测。重叠部分的大小可以自定义,重叠部分越多,图像增强的效果越连续,检测出的边缘也越连续,但会增加运算量,而且连续改进的程度也不明显,本文作实验则采用重叠一行一列。一个图像分块子图递进重叠部分为一行一列所以增加的运算量约为1/8。但这样保证了图像边缘的连续性。
这样经过模糊增强后,图像的各区域之间层次比较清楚而且边缘两侧的灰度对比增强,其提取的边缘信息也就会更加精细。
4 模糊增强实验结果
待处理的256×256的house图像如图2(a)所示,每一个像素均可以是256个灰度级(0,1,…255)中之一。增强迭代的次数≤2时,模糊增强的效果并不明显。当迭代次数>2时模糊增强的效果很好;迭代次数>1时,增强变化趋于平缓。
表1中C为模糊阈值带宽;Fe为模糊倒数型因子。根据图像的这两个因子可以计算出模糊指数性因子Fd。
为了突出实验效果的差异,本文的图像模糊增强实验是根据不同的模糊因子多次迭代增强的效果如表1所示,W为图像窗口的大小,分别为2×2,3×3,5×5,8×8,10×10.经过多次试验表明W取2~10能够看到输出的轮廓;当W=5~8时,可以得到比较满意的效果。模糊阈值带宽的选取C对于256×256的house图来说取值在20~50比较合适[10]。对于倒数因子Fe取2 ~ 3为佳,本实验中以Fe=2为例。根据大量实验得到,所有这些所取得最佳值不一定相同,但不会相差很远,这主要取决于被处理图像的灰度分布。

表1 不同模糊因子对应的图像
图2中(a)为原图,对于此图从多次迭代模糊增强的效果来看可以得到以下结论:
1)随着W增大图像层次会逐渐加强但图像的细节会有所丢失;
2)随着C的增大图像模糊的区域越来越大同样也会损失图像部分有用信息;
3)W=5~8且C=30时效果较佳,有利于模糊边缘提取[11]。
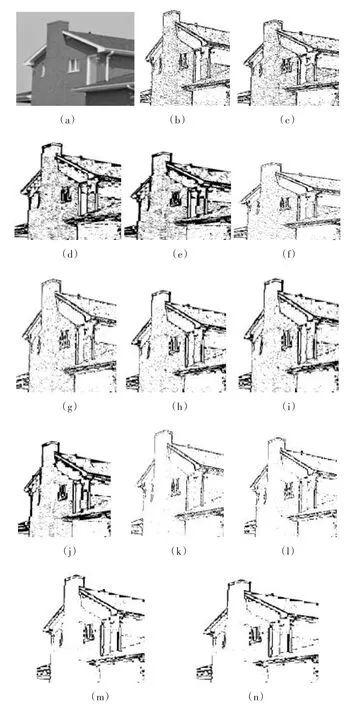
图2 不同模糊因子下图像模糊增强图
5 结语
实验表明,由于模糊增强技术利用灵活的选取模糊因子,改进处理效果,它比常用的直方图平坦化(Histogram Equalization)方法效果更好。如何利用模糊集合理论,开发数字图像处理新的工具,是我们正在研究的课题。可以预言,在不久的将来模糊集合的思想将会应用于数字图像处理的更多领域。
