基于量子行为和差分进化的改进蜻蜓算法
2019-03-24曹紫阳贾文友梁利东江磊
曹紫阳,贾文友,梁利东,江磊
(安徽工程大学机械与汽车工程学院,安徽 芜湖 241000)
0 引言
蜻蜓算法(Dragonfly Algorithm,DA)是Seye-dali Mirjalili提出的一种新的群智能优化算法,其通过模拟蜻蜓捕食和迁徙的两种群体行为来实现算法[1]。因DA原理简单、易于实现以及具有一定的寻优能力,在国外已被成功应用于电力负荷的精准预测模型[2]、电力系统电压稳定性评估[3]、智能电网系统的潮流管理[4]等领域。其中,傅军栋等[5]应用DA优化支持向量机并用于解决变压器故障诊断问题,但没有研究算法的收敛速度;宋俊敏[6]应用DA解决甘蔗收获机的结构性能的优化问题,取得了较好的优化效果,但是其精度较差;赵齐辉等[7]提出将差分进化算法融入到DA中,有效提升了DA的收敛速度和求解精度,但在处理实际复杂问题时易陷入局部极小值和出现早熟等现象。
研究发现量子粒子群算法的学习机制有助于解决算法容易陷入局部最优解和出现早熟等缺陷问题[8-9],差分进化策略借助变异、交叉操作有助于克服算法在运算后期种群多样性丧失等缺陷问题[10],针对上述情况,本文提出量子行为和差分进化融合策略优化蜻蜓算法(Quantum-behaved and Differential Evolution Dragonflfly Algorithm, QDEDA)。在实验验证部分,选取8个标准测试函数对QDEDA进行测试,并与原始DA、灰狼算法(GWO)、粒子群算法(PSO)的运行结果进行实验对比。
1 DA概述
蜻蜓具有两种独特的群体行为:捕食和迁徙,前者为静态群体,后者为动态群体。这两种群体行为与元启发式算法的探索和开发阶段非常相似,由此Seyedali Mirjalili提出DA,他指出蜻蜓种群中个体依靠5种行为进行位置更新,即分离度、对齐度、内聚度、食物吸引力和天敌排斥力,具体数学模型如下。
(1)
式(1)是分离度Si的数学模型,式中:Si表示第i个个体的分离度;X表示当前蜻蜓个体的位置;Xj表示第j个相邻蜻蜓个体的位置;N表示与第i个蜻蜓个体相邻的个体数量。
(2)
式(2)是对齐度Ai的数学模型,式中:Ai表示第i个个体的对齐度;Vj表示第j个相邻蜻蜓个体的速度。
(3)
式(3)是内聚度Ci的数学模型,式中Ci表示第i个个体的内聚度。
Fi=X+-X。
(4)
式(4)是食物吸引力Fi的数学模型,式中:Fi表示食物位置对第i个个体的吸引力;X+表示食物源位置。
Ei=X-+X。
(5)
式(5)是天敌排斥力Ei的数学模型,式中:Ei表示天敌位置对第i个个体的排斥力;X-表示天敌位置。
根据上述5种蜻蜓行为,下一代蜻蜓的位置和位置更新步长由式(6)和(7)进行计算。
ΔXt+1=(sSi+aAi+cCi+fFi+eEi)+wΔX′;
(6)
Xt+1=Xt+ΔXt+1,
(7)
式中:t表示当前迭代次数;i表示第i个蜻蜓个体;Xt表示当前t代种群个体位置;ΔXt+1表示下一代种群位置更新步长;Xt+1表示下一代种群个体位置;s表示分离度权重;a表示对齐度权重;c表示内聚度权重;f表示食物因子;e表示天敌因子;w表示惯性权重。
Seyedali Mirjalili假设每个蜻蜓个体都是处于半径为r的圆的圆心,如果个体i与个体j之间的距离小于r,则认为个体i与个体j相邻,为了加快收敛速度,半径r随着迭代次数的增加而增加。当没有任何个体与个体i相邻时,为提高蜻蜓搜索时的随机特性,引入Le′vyflight随机游走方法。游走步长满足一个heavy-tailed的Le′vy分布[11],由式(8)进行计算。
(8)
式中:r1、r2是[0,1]之间的随机数;β是一个常量(此处取1.5);σ由式(9)计算。
(9)
式中Γ(x)=(x-1)!。
当没有任何相邻个体时,使用莱维飞行公式(10)进行位置更新。
Xt+1=Xt+Le′vy(d×Xt),
(10)
式中d表示位置向量的维数。
2 DA的改进
2.1 量子行为位置更新机制

(11)

(12)
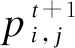
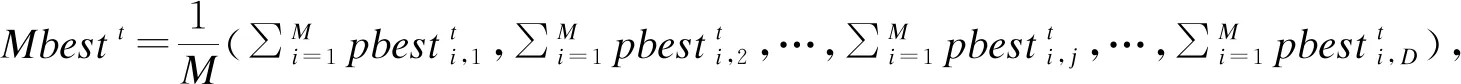
(13)
式中:M是种群大小;Mbestt为种群中蜻蜓个体历史最优位置的平均值。
综上,由式(11)~(13)可知,个体的当前位置与平均最优位置之间的距离决定了下一次个体的位置,由此使得个体在自身局部吸引子周围进行全局游走,即量子行为位置更新机制。其实现机制在吸取种群当前最优基础上,还参考了历史最优位置,增强了QDEDA的全局搜索能力。
2.2 差分进化寻优策略
QDEDA融合的差分进化寻优策略,有利于提高优化非线性、多峰值等问题的能力。该策略包含变异、交叉、选择3种操作,与遗传算法的原理类似。在每次迭代结束后对当前最优解进行一次交叉和变异,随后进行选择操作,如果求得适应度更好的解,则替换当前最优解,否则继续下一次迭代,以此引导蜻蜓优化算法向最优解方向搜索,因此增强了信息交流,提高了原始DA的收敛速度和寻优精度。
1)变异操作
(14)
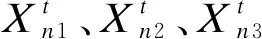
2)交叉操作
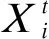
(15)
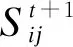
3)选择操作
在差分进化寻优策略中,使用了贪婪算法机理来选择进入到下一代的个体,确保种群的进化方向,即当子代产生了适应度更好的解时,用此解来替代最优解,否则进行下一次迭代运算,选择操作如式(16)所示。
(16)
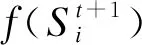
2.3 QDEDA流程与步骤
QDEDA将量子行为位置更新机制和差分进化寻优策略融入原始DA,分别改进了算法中蜻蜓个体的位置更新方式和增强了算法中的信息交流,其流程如图1所示,具体步骤如下。
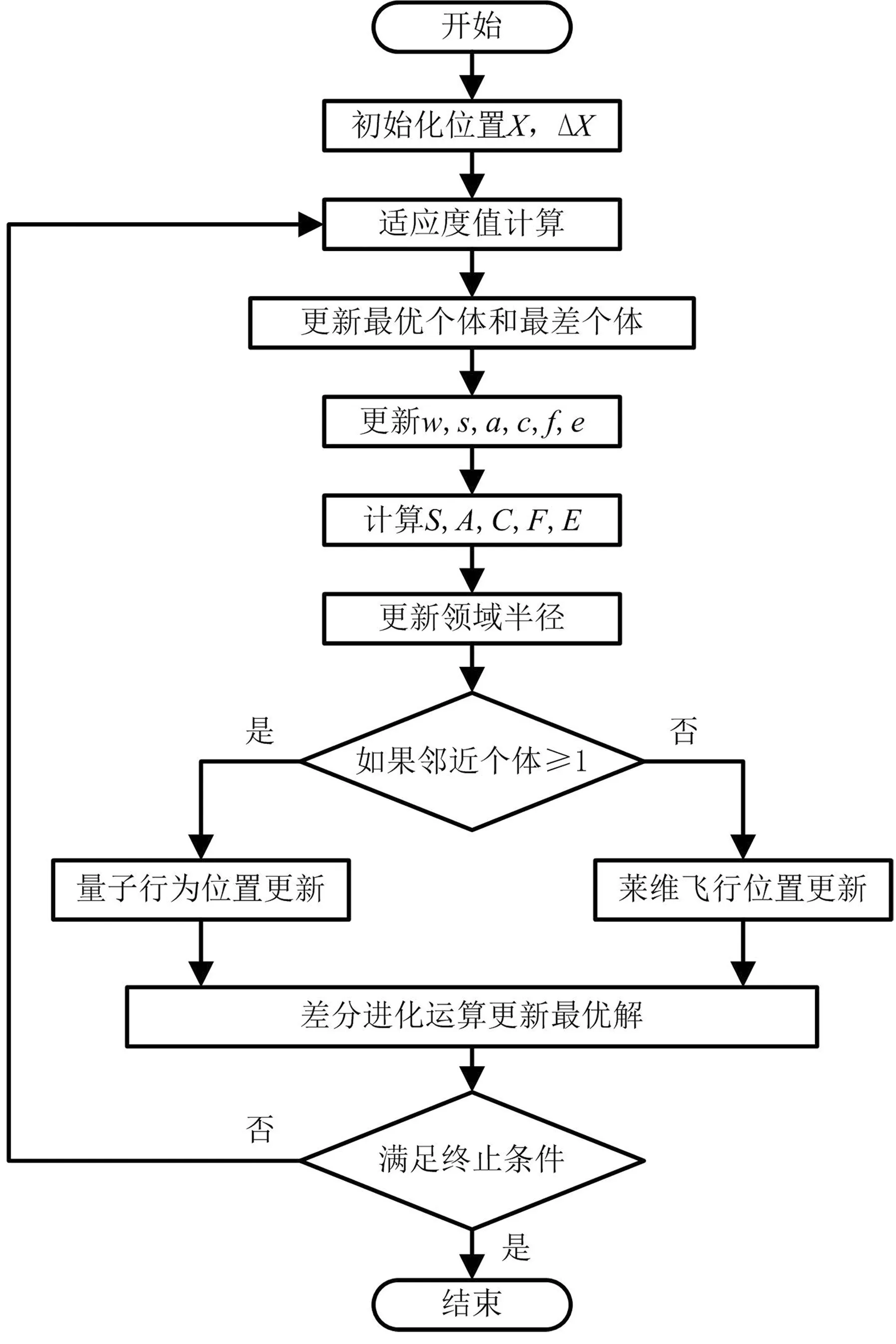
图1 QDEDA算法流程图
步骤1算法参数初始化:设置种群规模N、空间维数D、最大迭代次数MIT、惯性权重w、领域半径r;随机初始化蜻蜓位置X和步长向量ΔX。
步骤2计算所有蜻蜓个体的适应度,更新最优个体为食物,最差个体为天敌。
步骤3更新权重5种行为因子s、a、c、f、e,利用式(1)~(5)计算分离度S、对齐度A、内聚度C、食物吸引力F、天敌排斥力E。
步骤4调用QDEDA融合的量子行为位置更新机制,更新领域半径r,若蜻蜓个体周围有临近个体,则调用式(6)和(12)更新个体的步长和位置;若蜻蜓个体周围没有临近个体,则调用莱维飞行式(10)更新个体位置。
步骤5调用QDEDA融合的差分进化寻优策略,使用式(14)~(16)对蜻蜓个体进行差分进化运算更新最优解。
步骤6判断是否满足终止条件,若达到最大迭代次数MIT则进入步骤7,否则返回至步骤2。
步骤7输出最优个体位置及全局最优解。
3 仿真实验与分析
3.1 测试函数与参数设置
为了有效评价QDEDA在收敛速度和寻优精度方面的性能,选取了8个国际上通用的测试函数,从最优解、最差解、平均解、均方差4个方面对比QDEDA和原始DA、GWO和PSO之间的求解效果。如表1所示,8个测试函数中f1(x)~f4(x)为4个单峰函数,函数名依次是Sphere、Schwefel 2.22、Schwefel 1.2、Schwefel 2.21;f5(x)~f8(x)为4个多峰函数,函数名依次是Rastrigin、Ackley、Griewank、Penalized 1.2,8个测试函数的维数均为30,最小值均为0。实验参数设置包括:种群规模N=40,最大迭代次数MIT= 500;原始DA中,w为0.2~0.9,s=0.1,a=0.1,c=0.7,f=1,e=1;GWO的距离控制参数ainitial=2,afinal=0;PSO的学习因子c1=c2=2,个体速度限制为[-6 ,6];实验对每个测试函数均运行30次。
3.2 实验环境及结果分析
实验环境为Windows 10操作系统,8 GB内存,Intel(R)Core(TM)i7-8750H CPU@ 4.1 GHz处理器,实验均用MATLAB R2018a运行。表2列出了4种算法在独立运行30次后最优解、最差解、平均解、标准差4个方面的运行结果。表3列出了4种算法的运行时间。
由表2可知,DA、GWO和PSO的运行结果时好时差,但是QDEDA在最优解、最差解、平均解、标准差4个方面稳定且基本优于DA、GWO和PSO;

表1 标准测试函数
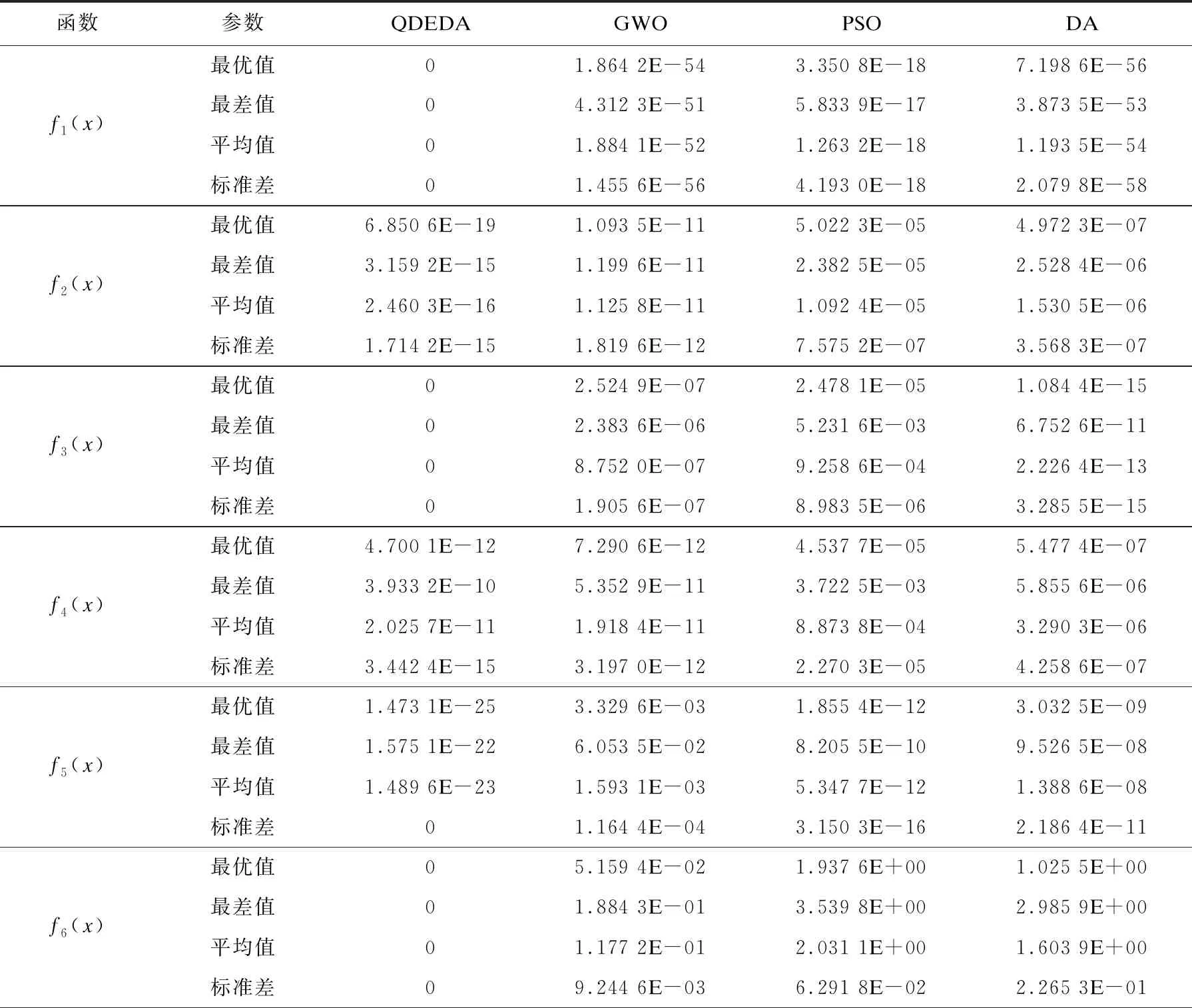
表2 算法寻优性能比较
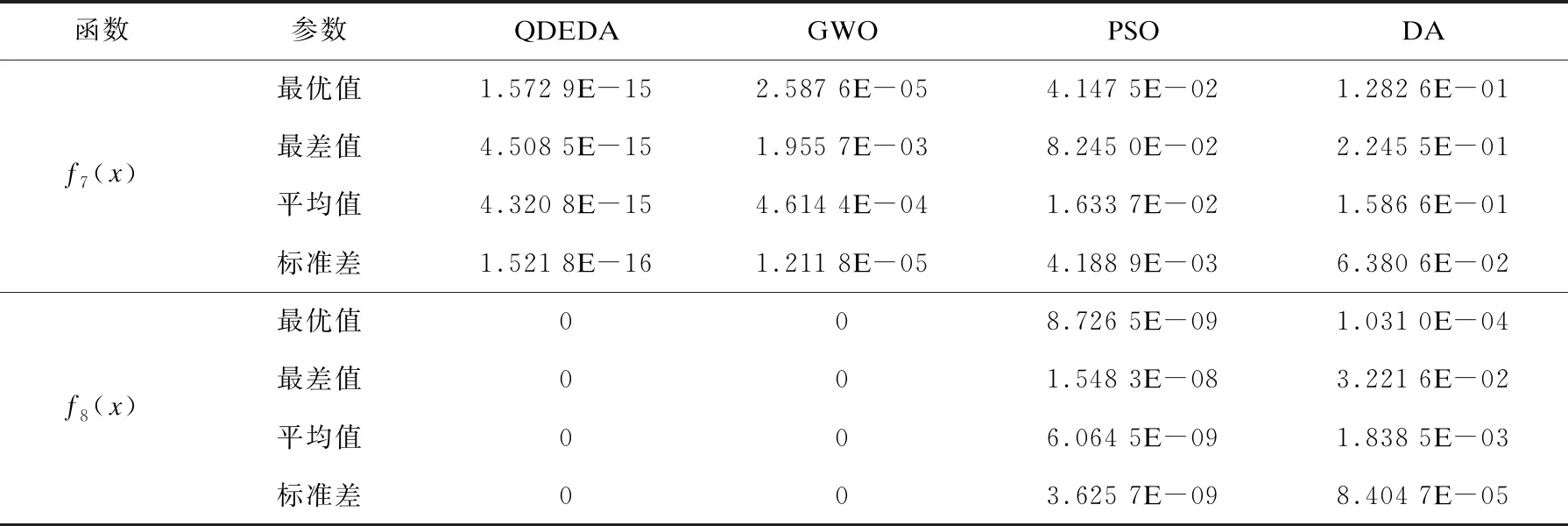
表2(续)

表3 运行时间分析 s
在标准差方面,QDEDA的寻优精度均能达到10的-15次方;在f1(x)、f3(x)、f6(x)、f8(x)4个测试函数中,QDEDA的最优值均能收敛到最小值0,可见QDEDA具有较高的寻优精度和较强的鲁棒性。由表3可知,在8个标准测试函数的运行时间中,QDEDA的运算时间均优于其他3种算法,证明了QDEDA的收敛速度得到了较大提升。
图2和图3分别表示4种算法在4个单峰函数和4个多峰函数上经过30次实验所得的收敛曲线。其中,由图2(a)、图3(b)和(c)可知,3个测试函数f1(x)、f6(x)、f7(x)的收敛曲线表明QDEDA的收敛速度明显优于其他3种算法,均在50代左右就能达到最优值;由图3(a)和(b)可知,测试函数f5(x)、f6(x)的收敛曲线表明QDEDA能快速收敛到全局最优值,尤其在迭代后期,QDEDA融合的差分进化寻优策略增强了算法的收敛速度;由图2(b)、图3(a)和(c)可知,3个测试函数f2(x)、f5(x)、f7(x)的收敛曲线表明原始DA、GWO和PSO均发生早熟并陷于局部最优解的现象,但是QDEDA融合的量子行为位置更新机制,既提高了种群多样性,又避免陷入早熟,始终朝着最优解的方向寻优。
4 结论
本文通过分析及研究DA,针对DA收敛速度慢、求解精度低、易陷入局部最小值和易出现早熟等缺陷问题,结合量子粒子群算法的学习机制和差分进化策略的变异、交叉、选择操作特性,提出了一种改进的QDEDA,该算法是将量子行为位置更新机制和差分进化策略融合到DA中。借助8个标准测试函数进行仿真实验,实验结果表明改进的QDEDA效果明显,在算法收敛速度和寻优精度、跳出局部最优解的能力等方面均优于原始DA、GWO和PSO。下一步的研究内容是将改进QDEDA应用到基于能量管理策略优化机器人轨迹规划运动的实际工程优化问题中。

(a)函数f1(x)收敛曲线 (b)函数f2(x)收敛曲线
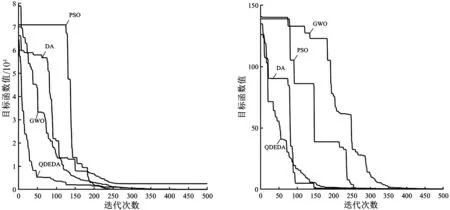
(c)函数f3(x)收敛曲线 (d)函数f4(x)收敛曲线图2 4个单峰函数收敛曲线
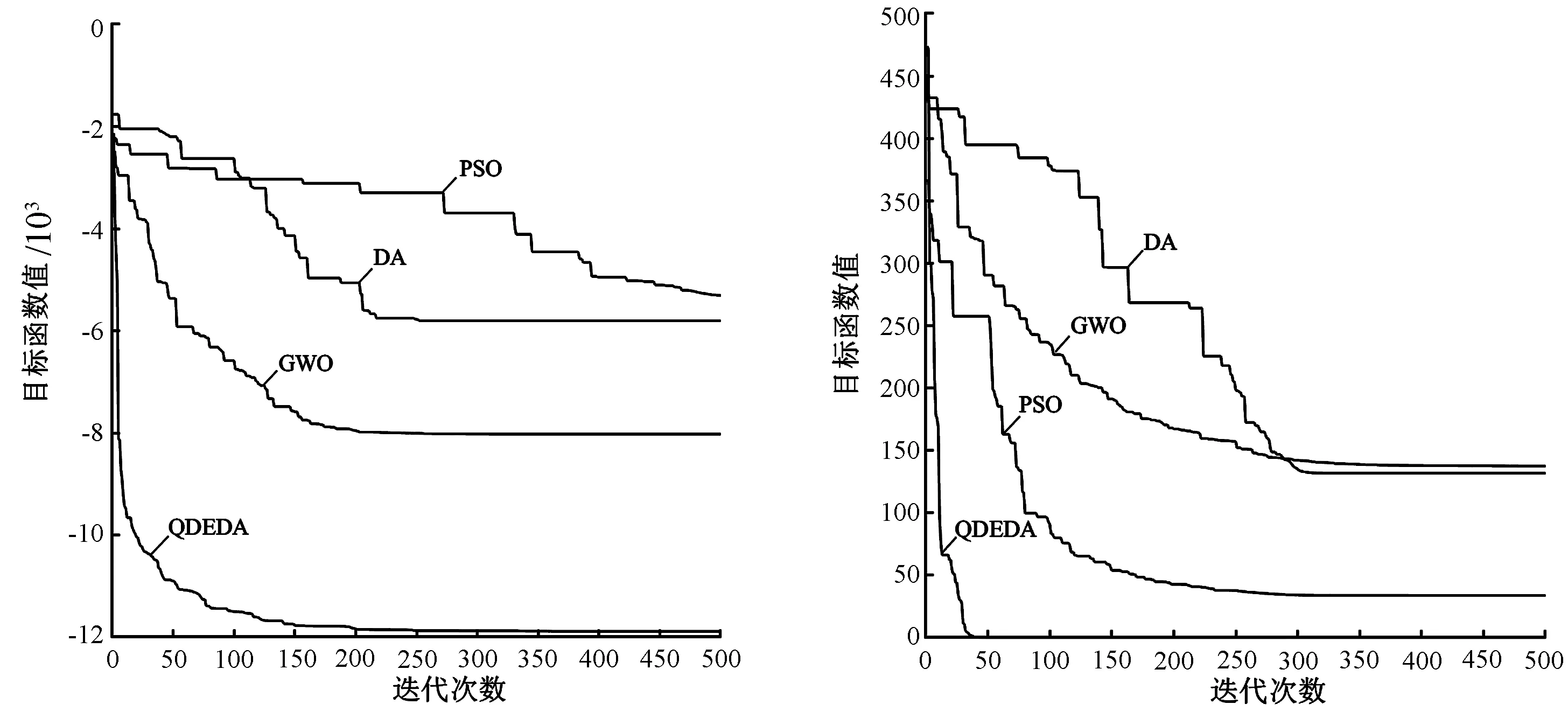
(a)函数f5(x)收敛曲线 (b)函数f6(x)收敛曲线
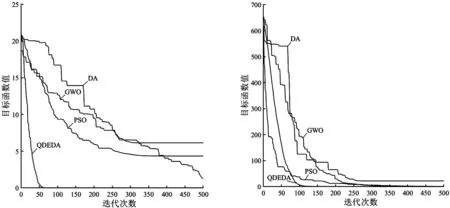
(c)函数f7(x)收敛曲线 (d)函数f8(x)收敛曲线图3 4个多峰函数收敛曲线
