地铁突发运营中断下应急公交调度研究

陈治亚，谭斐，冯芬玲

地铁突发运营中断下应急公交调度研究

陈治亚，谭斐，冯芬玲

(中南大学 交通运输工程学院，湖南 长沙 410075)

针对公交桥接疏运车辆调度中“疏运需求远超单辆公交车辆运能”的特征，考虑客流疏运时限的要求，允许公交车辆跨线运行，建立以公交车辆总疏运时间最小为目标的公交桥接疏运集中循环调度模型，提出“虚拟疏运目的地”的新概念，将模型转化为整数线性规划模型，最后进行实例论证模型的有效性及灵敏度分析。结果表明，模型能有效提高公交桥接疏运效率，降低疏运成本。

地铁；突发运营中断；公交桥接疏运；集中循环调度优化模型

地铁具有节能环保、高效安全等诸多优点，目前已被视为减轻城市拥堵问题的最佳方式之 一[1−2]。城市对于地铁高度依赖性使地铁一旦发生突发运营中断事件，将对整个城市交通系统产生难以估量的冲击与影响[3]。运营中断是地铁由于受到突发事故、设备故障和大客流等因素影响，造成列车在线路上运行中断或产生较大延误，既定列车运行计划需大规模调整的事件[4]。Pender等[5]调查了不同国家的48个地铁运营组织，发现公交桥接疏运服务广泛应用于其处理地铁突发运营中断。公交桥接疏运是指在地铁运营突发中断时，地铁运营部门启用临时公交服务替代地铁桥接中断车站，恢复部分地铁网络连通性，从而减轻乘客的出行损失，保证公共交通可靠性的一种措施。多数关于公交桥接疏运的研究致力于使用公交桥接受影响车站，恢复地铁网络的连通性，它们大都采用Kepaptsoglou等[6]基于交通路径网络规划问题(TRNDP)提出的公交桥接疏运网络设计框架：设计公交桥接疏运路线、为路线配置公交资源。JIN等[7]依据上述的设计框架，使用列生成算法产生候选路线，建立多商品网络流模型来选取最优路线组合，最后通过一个优化程序同时配置公交资源以及相应的路线频率。姚加林等[8]利用正常运营的常规公交以及临时运营的应急公交建立联合交通运输组织方案。这些研究大都调配公交资源在既定路线上按照固定的发车频率进行疏运乘客，但这种固定发车频率的策略只适用于有计划的地铁运营中断，或是在长时间的地铁运营中断中替代地铁运输日常乘客[9]。一旦发生突发的无计划的地铁运营中断，地铁车站将会短时间内聚集大量的乘客，使得公交车辆到达车站后立即满载，这种固定发车频率的策略显然不合时宜。突发的地铁运营中断在很大程度上具备大型活动或突发事件的许多特征，因此许多研究开始采用大型活动或突发事件“满载即走”的灵活发车策略，形成了针对特定桥接疏运路线的应急公交调度问题。WANG等[10]以总疏散时间最小为目标，分别以地铁站和公交中转站为疏散目的地建立公交应急调度模型；模型1假设总公交运能大于乘客需求，公交车辆无需进行循环疏运。模型2引入公交车辆循环次数作为决策变量建立模型，基于胡华磊[11]提出的等效驻车点的概念，人工指定公交车辆最大循环次数设为固定值进行求解模型。胡华等[12]不再人工指定车辆循环次数，而是以公交车辆循环次数作为决策变量建立公交应急调度模型，进而运用改进遗传算法中求解模型；然而，上述研究均采用1辆公交只可在特定的1条路线上运行，不允许跨线运行的运行策略，极大地限制了车辆调度的灵活性，使得车辆的运能无法得到充分利用，以此运行策略建立的模型称之为独立调度模型[13]。因此，本文在上述研究的基础上，同时将地铁中间折返站与临时中转站作为疏运目的地，考虑客流疏运时限的要求，允许公交车辆跨线运行，以公交循环次数为决策变量，建立以公交车辆总疏运时间最小为目标的公交桥接疏运集中循环调度模型，此外，提出“虚拟疏运目的地”的新概念，将模型转化为易于求解的整数线性规划模型，最后进行实例论证及灵敏度分析。

1 问题描述

地铁线路一旦发生运营中断，相关部门将会对事件进行评估响应，根据事件的严重程度和发展态势，将应急响应设定为Ⅰ级，Ⅱ级，Ⅲ级和Ⅳ级4个等级。通常发布Ⅳ级响应后将会加大线路沿线地面公交发车频率，而发布Ⅲ级及以上响应后，应急公交桥接服务将会被启动[3]。北京市在发生2~6 h运营中断事件即会启动Ⅲ级响应[14]，而上海市这一时间则为3~6 h[15]。由于突发事件的不确定性，运营中断地点可能发生在折返站、非折返站及它们之间的线路中的任何一处。其中，折返站是指设有折返线，可以改变列车运行方向的车站，包括首、末站及首末站之间的中间折返站，国内线路大多设有2个及以上的中间折返站，如上海地铁2号线设有近10个中间折返站，因此，运营中断将发生在以下3类地点，见图1。2个中间折返站之间(不含此2折返站)，起点站(终点站)与离之最近的中间折返站之间(含起点站(终点站))、离起点站(终点站)最近的中间折返站。中断发生后，地铁可在未受影响区段之间开行小交路，这样公交应急机制启动后，乘客将通过“公交桥接(中断区段)+小交路(未受影响区段)”的运输模式到达目的地。本文仅对中断点位于2个中间折返站之间(类型1)的情况进行研究。

运营中断发生之后，系统内客流可分为应急机制启动前滞留于系统内的静态客流和应急机制启动后仍陆续进入系统内的动态客流。由于动态客流不易获得，本文主要研究的是静态客流。

一旦发生运营中断，滞留于系统内的庞大客流将会对中间折返站和小交路产生巨大的负荷，为了缓解压力，同时满足非本线客流需求，可以选定某些地面公交站或其他地铁线路车站作为临时中转站用于分流，减少乘客延误。它们与2个中间折返站构成了疏运目的地。因此，本文研究的公交桥接疏运调度问题即为如何有效组织有限的公交资源，将滞留于系统内的客流快速安全地运送至疏运目的地。

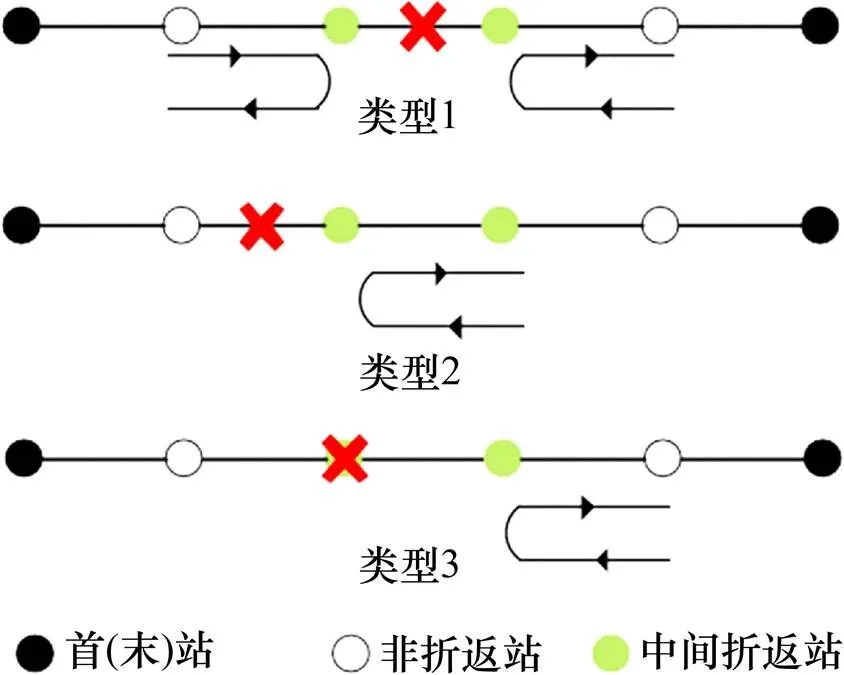
图1 地铁运营中断类型

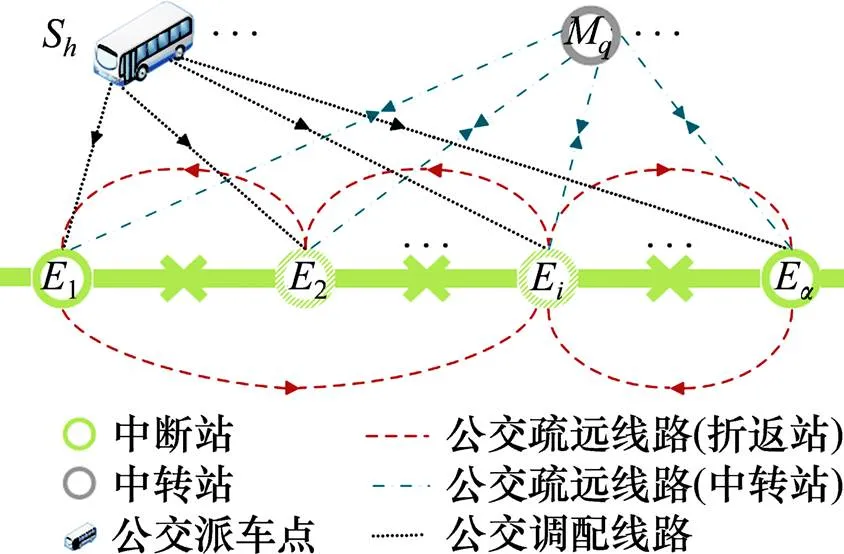
图2 公交调度拓扑结构图

图2为公交桥接疏运调度拓扑结构图。地铁中断站集合为{E|=1,2,…,}，其中1和分别代表中断区间两端中间折返站，临时中转站集合为{M|=1,2,…,}，其与中间折返站共同组成了疏运目的地{G|=1,2,…,,+1,+2}。公交派车点集合{S|=1,2,…,}，可用公交车辆集合为{B|=1,2,…,}。公交调度包含2个过程：车辆调配阶段和疏运阶段。在车辆调配阶段，公交车辆自公交派车点被调配至中断站；在疏运阶段，公交车辆在中断站和疏运目的地之间往返运行直至完成最后一次运输任务。其中，当疏运目的地为中间折返站时，车辆在沿途均逐站停靠，允许乘客上、下车。公交车辆集中于地铁中断站统一调配，采用在以同一中断站为起点，不同线路(以不同疏运目的地为终点)之间允许跨线运行的策略以发挥车辆最大使用效率，从而减少调车总数和总疏运时间。

2 优化模型

考虑问题的研究由简单到复杂，模型作如下假设：1) 中断站待疏运乘客需求经预测认为是确定的；2) 各公交车辆是等质的，其车容量和车速等参数为固定值；3) 公交车辆在各站点之间的行驶时间的确定的。

2.1 目标函数

以公交车辆总疏运时间最小作为优化目标，总疏运时间包含公交车辆自派车点调配至地铁中断站的总行驶时间和公交车辆在地铁中断站与疏运目的地之间往返运送乘客总行驶时间。

公交车辆从配车点调配至地铁中断站的总行驶时间1为：

其中：t,k表示公交车辆B为所在屯车点到中断站E的行驶时间；x,k为0-1决策变量，表示在车辆调配阶段，公交车辆B是否被调配至中断站E进行疏运任务，若是，x,k=1，否则x,k=0。

公交车辆在地铁中断站与与疏运目的地之间往返总行驶时间2为：

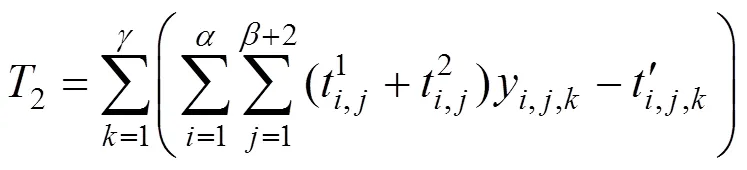
因此，模型的目标函数可表述为：

其中：为总疏运时间；为足够小的正数权重，式(3)第3项保证了若调配1辆公交无法减少总疏运时间，则此公交不会被调配。

2.2 约束条件

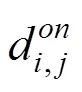
约束(7)保证了1辆公交车辆在调配阶段最多只能被分配至1个中断站：

约束(8)保证了1辆公交车辆可在以其所在的初始中断站为起点的任意路线上进行疏运任务，为足够大的正整数：

约束(9)保证了任意1辆公交车完成其疏运任务的时间不能超过客流疏运时限max，其中，客流疏运时限为相关部门依据实际情况确定，应小于运营中断持续时间：

约束(10)为决策变量约束：

3 优化算法

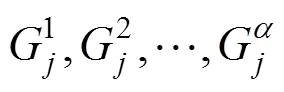
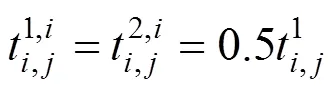
以此类推，将设置+2个与现实疏运目的地G(=1,2,…,+2)一一对应的虚拟疏运目的地G++2(=1,2,…,+2)。

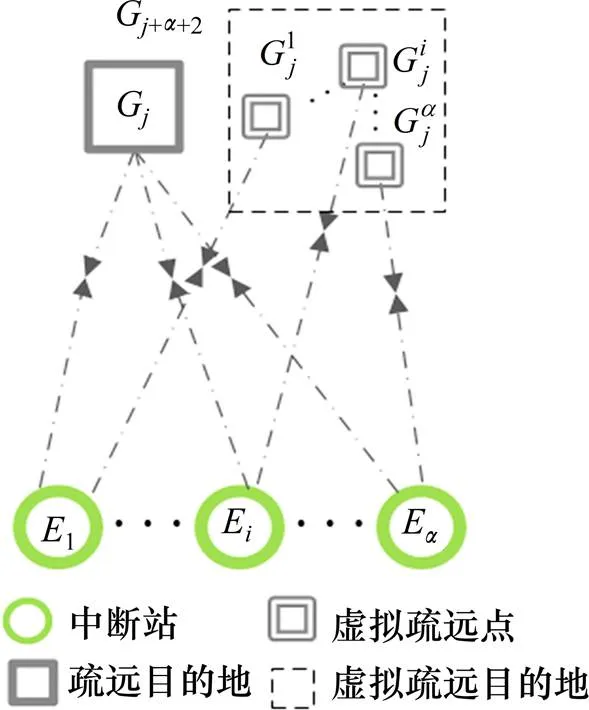
图3 虚拟疏运目的地示意图

因此，可将初始模型调整为：

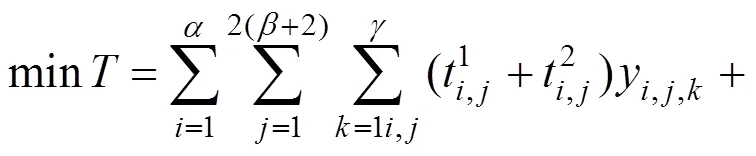
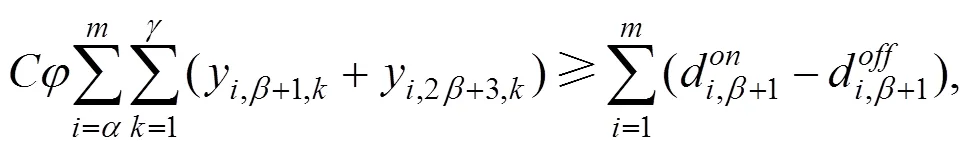
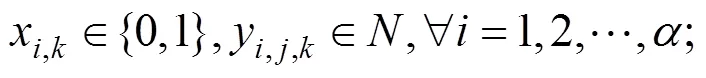
其中，约束(19)表示在疏运阶段，公交车辆最多往返1次虚拟疏运目的地，即公交车辆在执行完最后一次疏运任务后不再返回中断站。改进后的集中循环调车模型为整数线性规划模型，有相应成熟算法求解。

4 算例分析

4.1 算例数据与结果

已知C市某地铁线路于某日早高峰发生中断，如图4所示，中断发生点位于非折返站4和5之间，1和6是最靠近发生点的中间折返站，因此它们之间的线路全部中断，无法通行。相关部门迅速对事件进行预警评估，预计运营中断将持续3 h，对外紧急发布了橙色预警，并启动了Ⅲ级响应机制，组织地面公交进行应急疏运滞留旅客。相关部门根据客流需求选定2个临时中转站1和2，它们与中间折返站1和6共同构成了公交疏运目的地，记为1，2，3和4。线路附近有5个公交派车点，记为1，2，3，4和5，其备车能力分别为16辆、13辆、17辆、17辆和7辆。

图4 C市地铁运营中断示意图

表1为公交派车点与地铁中断站之间的行驶时间；中断地铁站客流上、下车人数见表2；表3为地铁中断站到各疏运目的地的车辆行驶时间。客流的最大疏运时限为90 min，公交额定载客量为80人/车，允许最大满载率设为1.2。根据案例的数据信息，使用MATLAB+YALMIP+CPLEX对集中循环调度模型进行求解，得到其车辆调度方案，将其结果与独立循环调度模型求解结果对比分析，见表4。

表1 公交派车点与地铁中断站之间的行驶时间

计算结果表明，独立循环调度模型与本文提出的集中循环调度模型均可在可用公交数有限的情况下完成地铁运营中断下的客流疏运任务。集中调度模型在总疏运时间及调车总数等指标上均优于独立循环调度模型：后者需要调用62辆公交，花费总疏运时间2 578 min，完成客流运输任务；而前者只需要调用55辆公交，总疏运时间为2 332 min，实际调车数减少12.7%，总疏运时间也减少9.6%。这是因为在独立循环调度模型中，由于客流疏运时限的存在，通常会出现这样一种情况：车辆回到客流发生点后，其剩余的行驶时间不足以完成对应路线的一次循环运输，因此这辆车的运能就损失了。而在集中调度模型中，允许车辆在不同路线上运输客流，车辆完成某条路线的运输任务后，能立刻投入到其他路线运输客流，这相当于整合车辆的运能以进行分配，从而减少调车数与总疏散时间。

表2 中断地铁站客流上、下车人数(人)

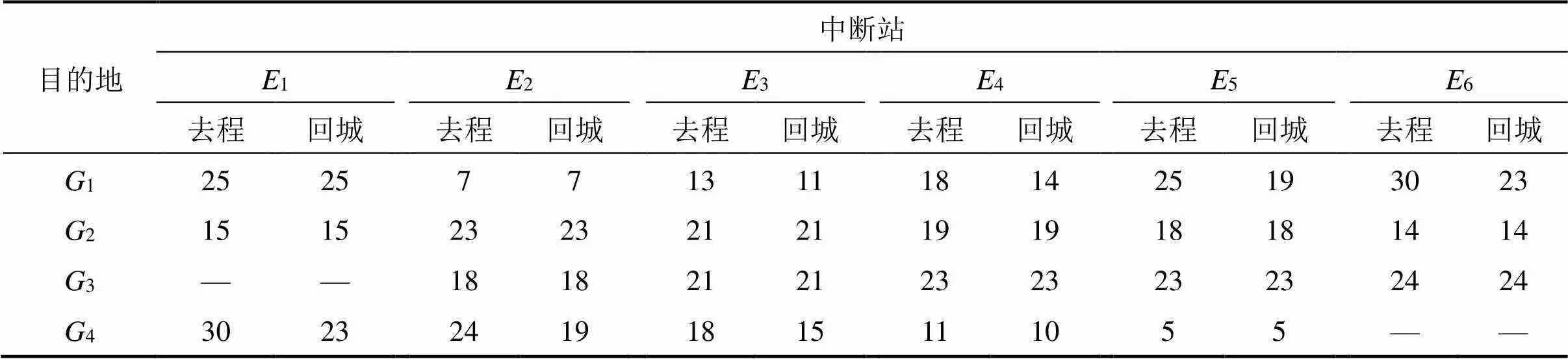
表3 地铁中断站与疏运目的地之间的行驶时间

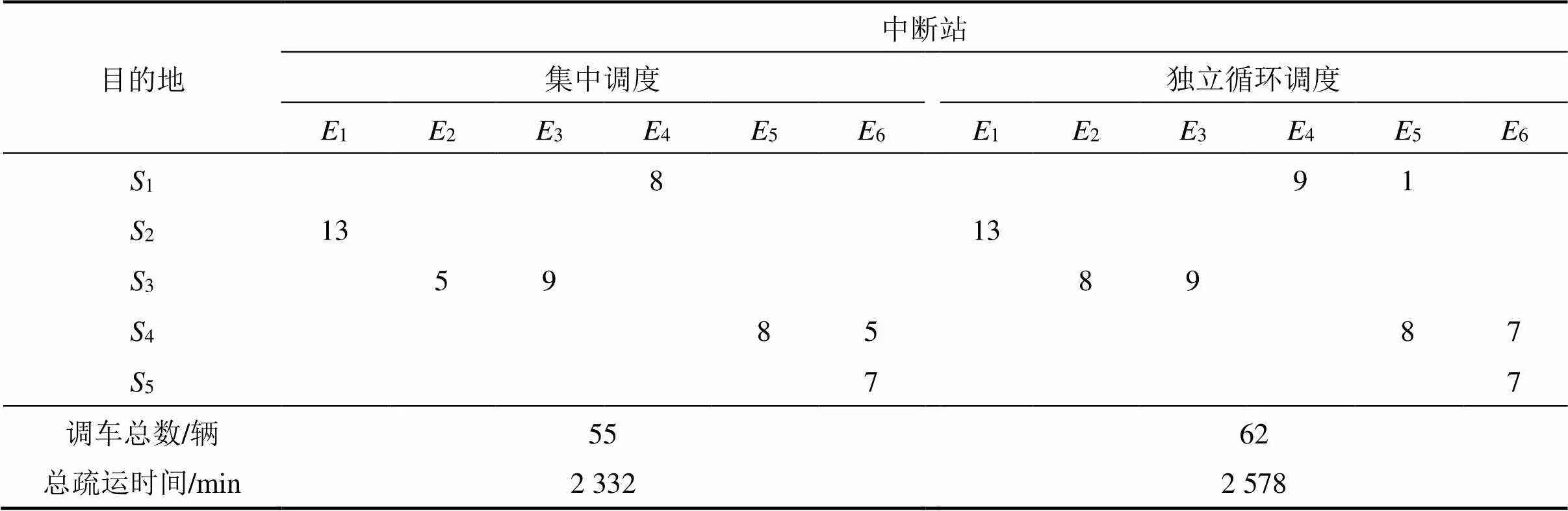
表4 优化模型输出结果

4.2 灵敏度分析

本文选取公交额定载客量、疏运客流需求及客流疏运时限等3个因素对其进行灵敏度分析，研究其变化对应急调度方案产生的影响[18]。

图5表示的是公交额定载客量的变化对于集中调度总疏运时间及实际调车数的影响。额定载客量以10为增量，从60增至140，随着额定载客量的增加，总疏运时间与实际调车数快速下降，说明增加车辆的额定载客量能有效地降低总疏运时间，减少调车数，然而总疏运时间与调车数下降的趋势随着额定载客量的增加越来越慢，例如，额定载客量从60增至70，总疏运时间减少了458 min，调车数减少了9辆；而从130增加到140，总疏运时间只减少了71 min，调车数只减少了1辆。因此一味地选用额定载客量大的公交车辆进行疏运工作，并不能有效降低总疏运时间，减少调车成本，反而会造成极大的资源浪费，相关部门应根据实际情况合理选用公交车辆。当公交额定载客量低于60时，模型无解，因此，要在规定的疏运时间1.5 h之内完成客流疏运任务，额定载客量必须高于60。

图5 额定载客量灵敏度分析

图6表示的是集中调度总疏运时间、实际调车数与疏运客流需求之间的关系。各客流需求基于原始客流需求，以0.1为增量进行变化，从0.5倍增至1.3倍，总疏运时间随之快速增长，且增长的幅度越来越大，从0.5倍增长到0.6倍，总疏运时间增加了108 min，而从1.2倍增长到1.3倍，总疏运时间则增加了602 min。调车数随着客流需求的增大而不断增加，当客流需求达到1.3倍时，所有可用公交均被调用。因此，相关部门应尽可能快而有效地向乘客传达紧急情况，使部分乘客自由选择其他旅行方式，以减少地铁站的客流需求，从而避免因客流需求过大而造成的总疏运时间过大、甚至无法满足客流需求的后果。

当客流需求超过原始客流需求的1.3倍时，现有的公交资源无法在1.5 h之内完成客流疏运任务，这时需要调整客流疏运时限以满足全部客流疏运需求。想要确定客流疏运时限，探究客流疏运时限对于公交调度方案的影响是必不可少的。本文研究了客流疏运时限从1~3 h公交调度方案的变化，见图7，当客流疏运时限小于1 h，无法生成调度方案。可以看到，随着客流疏运时限的增加，总疏运时间呈缓慢下降的趋势，而总调车数则呈急剧下降的趋势，具体原因分析如下：随着客流疏运时限的增加，已经调配的车辆在中断站与疏运目的地之间的往返次数随之增加，使得同样的客流需求下，所需的公交车数减少，但单辆公交行驶时间的增加使得总疏运时间变化较小。因此制定应急调度方案时，相关部门应考虑客流需求、可用公交数和乘客行为等因素，根据不同情况确定客流疏运时限。

图6 客流量灵敏度分析

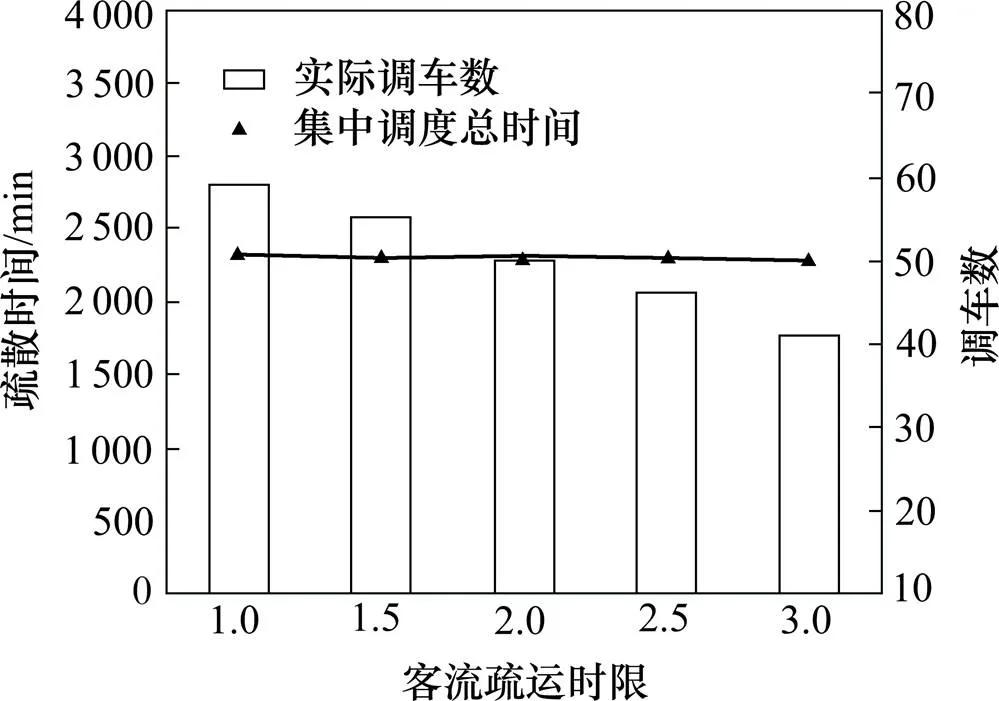
图7 客流疏运时限灵敏度分析

5 结论

1) 基于以折返地铁站和中转地铁站为疏运目的地的特定桥接疏运路线，以公交循环次数为决策变量，考虑客流疏运时限的要求，允许公交车辆跨线运行，建立应对地铁突发运营中断的公交桥接疏运集中循环调度模型，并且提出“虚拟疏运目的地”的新概念，将模型转化为整数线性模型。

2) 通过案例分析验证了模型的可行性，结果表明，集中循环调度模型在总疏运时间和实际调车数上都优于独立循环调度模型。

3) 对车辆额定载客量、客流需求和客流疏运时限等影响总疏运时间和实际调车数的因素进行灵敏度分析。结果表明，增加车辆额定载客量能有效减少总疏运时间和实际调车数，增加客流需求会使总疏运时间和实际调车数急剧增大，增加客流疏运时限能有效减少最小调车数，而客流疏运时限的增加对于总疏运时间的影响较小，却会使调车数急剧减小。

[1] KANG L, WU J, SUN H, et al. A case study on the coordination of last trains for the Beijing subway network[J]. Transportation Research Part B: Methodological, 2015,72:112−127.

[2] Alicia D, Gilbert Laporte, Juan A Mesa, et al. Evaluating passenger robustness in a rail transit network[J]. Transportation Research Part C, 2012, 20: 34−46.

[3] 滕靖, 徐瑞华. 地铁突发事件下公交应急联动策略[J]. 铁道学报, 2010, 32(5): 13−17. TENG Jin, XU Ruihua. Bus dispathing strategies in urban rail emergent events[J]. Journal of the China Railway Society, 2010, 32(5): 13−17.

[4] Pender B. Unplanned urban passenger raildisruption – new methods andperspectives on bus bridging[D]. Melbourne: Monash University, 2014.

[5] Pender B, Currie G, Delbosc A.Planning for the unplanned: an international review of current approaches to service disruption management of railways[C]//35th Australasian Transport Research Forum, 2012: 1−17.

[6] Kepaptsoglou K, Karlaftis M G. The bus bridging problem in metro operations: conceptual framework, models and algorithms[J]. Public Transport, 2009, 1(4):275−297.

[7] Jin J G, Teo K M, Odoni A R. Optimizing bus bridging services in response to disruptions of urban transit rail networks[M]. INFORMS, 2016.

[8] 姚加林, 齐弦. 城轨运营中断条件下公交应急线路开行方案研究[J]. 铁道科学与工程学报, 2018, 15(7): 1863−1870. YAO Jialin, QI Xian. Research on bus emergency route plan in the operation interruption of urban rail transit[J]. Journal of Railway Science and Engineering, 2018, 15(7): 1863−1870.

[9] GU W, YU J, JI Y, et al. Plan-based flexible bus bridging operation strategy[J]. Transportation Research Part C: Emerging Technologies, 2018, 91: 209−229.

[10] YUN Wang, YAN X, ZHOU Y, et al. Study of the bus dynamic coscheduling optimization method under urban rail transit line emergency[J]. Computational Intelligence & Neuroscience, 2014(6):1−8.

[11] 胡华磊. 大型活动突发事件公交应急调度的研究[D]. 北京: 北京交通大学, 2008. HU Hualei. Research on emergent bus scheduling in large activity[D]. Beijing: Beijing Jiaotong University, 2008.

[12] 胡华, 高云峰, 刘志钢. 地铁运营中断下公交桥接疏运车辆应急调度模型及算法[J]. 铁道学报, 2018, 40(5): 31−37. HU Hua, GAO Yunfeng, LIU Zhigang. Model and algorithm for bridging bus emergency dispatching problem during metro operational disruptions[J]. Journal of the China Railway Society, 2018, 40(5): 31−37.

[13] 滕靖, 陈宇毅. 大型活动下配合城轨交通客流集散的公交调度[J]. 系统工程理论与实践,2012, 32(4): 895− 902. TENG Jin, CHEN Yuyi. Bus dispatching method for associating with urban rail transit to transport passengers during large-scale events[J]. System Engineering Theory and Practice, 2012, 32(4): 895−902.

[14] 北京市政府. 北京市轨道交通运营突发事件应急预案[R]. 北京, 2016. Beijing Municipal Government. Emergency plan for Beijing urban rail transit emergency[R]. Beijing, 2016.

[15] 上海市政府. 上海市处置轨道交通运营事故应急预案[R]. 上海, 2016. Shanghai Municipal Government. Emergency plan for Shanghai urban rail transit emergency[R]. Shanghai, 2016.

[16] Schöbel, Anita. Line planning in public transportation: models and methods[J]. Or Spectrum, 2012, 34(3): 491− 510.

[17] Avishai CEDER. Public transit planning and operation: Theory, modeling and practice[M]. Amsterdam, The Netherlands: Elsevier, 2007.

[18] Antonio P, Luca D, Marilisa B, et al. A sensitivity analysis of recovery soulution in the case of rail disruption management[C]// Transportation Research Board, 2015.

Study of the bus dispatching under metro emergent operational disruptions

CHEN Zhiya, TAN Fei, FENG Fenling

(School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

In this paper, a bus emergency centralized cycle dispatching optimization model to minimize the total evacuation time of all of the stranded passengers was proposed. In the model, the feature of evacuation demand far exceeding bus capacity and the passenger bridging time limits were taken into account. Buses were allowed to flexibly serve different bridging routes. In the model solution process, a new concept-the virtual evacuation destination was proposed to transform the model into an integer linear programming problem. A case study was conducted to verify the feasibility of the model. Also, sensitivity analysis of vital factors was carried out to analyze their effects on the total evacuation time. The results show that the model can effectively improve the efficiency and reduce the cost of the bus bridging service.

metro; emergent operational disruption; bus bridging; centralized cycle dispatching optimization model

U293

A

1672 − 7029(2019)09− 2360 − 08

10.19713/j.cnki.43−1423/u.2019.09.031

2018−12−29

国家重点研发计划项目(2018YFB1201402)

陈治亚(1958−)，男，湖南岳阳人，教授，从事交通运输规划与管理研究；E−mail：chzy@csu.edu.cn

(编辑 阳丽霞)