考虑时间价值成本的中欧笔记本电脑多式联运路径优化研究

刘畅，关秀婷，张金伟，计明军

考虑时间价值成本的中欧笔记本电脑多式联运路径优化研究

刘畅，关秀婷，张金伟，计明军

(大连海事大学 交通运输工程学院，辽宁 大连 116026)

针对笔记本电脑高时效、高价值的特性构建时间价值成本模型，同时考虑多产地和多品级的特点，以综合物流成本最低为目标，建立多式联运路径选择优化模型，先将模型的运输网络通过新增虚拟节点进行变形，然后采用深度优先搜索的算法对路径选择优化模型进行求解。通过中欧笔记本电脑出口案例进行验证，结果表明：陆桥运输和空运相比于海运，在运输笔记本电脑这一高价值信息产品时的综合物流成本更低，最后探究价值变化对路径选择的影响，为中欧之间货物运输提供 参考。

时间价值成本；多式联运；路径优化；中欧班列；笔记本电脑运输

随着经济和贸易全球化进程的加快，对运输的要求也越来越高，运输过程中产生的时间价值成本是一个重要的影响因素，笔记本电脑作为一种高价值、时效优先性信息产品，考虑运输过程中的时间价值成本十分必要。我国作为世界上最大的笔记本电脑出口国，对欧洲出口量约占我国出口量的1/5，“一带一路”倡议的大力推进，为中欧之间的贸易运输发展提供了动力和支撑，近年来，以中欧班列为代表的欧亚大陆桥运输发展迅速，已经成为中欧之间的重要运输通道，与传统的中欧海运、数量众多的中欧空中航线构成了较为完善的中欧运输体系，由此，在考虑时间价值成本的前提下对中欧之间笔记本电脑多式联运路径优化进行研究具有很重要的现实意义。多式联运路径优化的研究多是关于时间和运输费用2个方面，李博[1]在对4种运输方式详细分析基础上构建以时间为约束、成本最小为目标的网络优化模型；杨洋等[2]结合煤炭作为大宗物资转运费用较高的特点，构建煤炭运输的多式联运路径优化模型；杨文东等[3]建立货物时间窗与路径优化模型的硬时间窗的双层优化模型；王清斌等[4]考虑运输方式转换过程中节点作业随机特征对运输方式和路径选择的影响，并建立带有时间约束的混合整数规划模型；张小龙等[5]引入混合时间窗约束建立多目标多式联运路径优化模型；吴晓莉 等[6]以汽车销售为背景，研究多式联运运输情况下，带时间窗的单个供应商到多个零售商的路径选择问题；ZHANG等[7]将多式联运整合进多个时期、多个阶段的生物质燃料供应链中并建立以成本最低为目标的数学模型；GUO等[8]考虑订货型制造企业中存在的带有取货时间约束和运输方式选择等特征，建立碳排放和运输成本的双目标混合整数非线性模型；HAO等[9]考虑货物运输的时间、成本和质量，建立一种基于动态规划并满足时间的约束条件的模型。已有的文献多是从建模和求解方法进行研究，在研究运输时间时，一般将时间作为约束条件，而本文在考虑货物自身高时间价值的基础上将时间作为总成本的一部分进行考虑。随着“一带一路”倡议的提出和中欧班列的发展，学者们也越来越关注中欧运输的研究，一些学者分别从中欧班列的意义和存在的问题[10−11]、价值量[12]、货物价值特性[13]进行深入探讨，李玉民等[14]构建考虑运输时间、运输费用、碳排放的中欧集装箱多式联运路径优化的多目标优化模型，并确定3个目标不同权重通过加权求和转化为单目标问题求解；Seo等[15]从时间、成本、风险、距离等角度分析研究重庆出口鹿特丹的笔记本电脑出口的七条路线。现有关于中欧运输的研究，多是关注陆桥运输和陆海联运，很少关注空运对中欧运输的现实意义。而本文站在生产企业的角度，综合研究分析中欧之间的公铁陆桥联运、公铁海联运以及空中运输等运输通道，构建笔记本电脑的时间价值成本模型，同时又考虑笔记本电脑的多品级、多产地的特点，以综合物流成本最低为目标构建多式联运路径选择优化模型，对运输方式和路径进行选择优化，为实际的中欧多式联运路径选择提供参考。

1 问题描述

我国两大笔记本电脑生产基地位于深圳和昆山，所生产的笔记本电脑可以通过多种运输方式出口到欧洲汉堡，其运输路线如图1所示，产品从产地出发，可以直接在产地或通过国内转运(公路或铁路)后经空运或海运运抵目的地，也可以先经国内转运(公路或铁路)运输到中欧班列起始站进行转运，经中欧班列运至班列终点站，由于班列终点站并不一定是目的地，所以需经国外转运(公路或铁路)至目的地。图中以相同的颜色表示班列的起始站和终点站，如成都—罗兹，概括来说其运输路径可以分为以中欧班列为基础的陆桥运输、陆海联运和空运等三大运输通道。本文研究的内容是在考虑时间价值成本情况下，以综合物流成本最低为目标，将这2个产地不同数量、不同品级的笔记本电脑，通过多式联运的方式运输至目的地，并得出最优运输方案。

图1 笔记本电脑运输路径图

2 数学模型

2.1 货物时间价值成本模型

本文将货物在运输过程所消耗的时间给货主带来的货币损失量称为货物时间价值成本，由资金占用时间成本和货物自身价值损失成本2部分构成。

2.1.1 资金占用时间成本

货物本身具有价值，对资金占用时间成本，在货物运输的过程中会带来资金的闲置，不仅对企业发展不利，也会给资金周转带来不便；若是企业生产资金来自银行贷款，也会产生利息成本。所以本文考虑资金占用时间成本时，按照银行贷款利息计算，再依据货物本身的价值和货物运输的时间，建立如下模型：

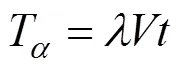
其中：为货物的资金占用时间成本；为银行每天贷款利息；为货物的总价值；为运输总时 间，d。

2.1.2 货物自身价值损失成本

货物运输产生的时间会对自身价值造成不利影响造成一定的资金成本。首先货物随着时间的不断增加而呈现贬值甚至失效，笔记本电脑作为信息产品，具有时效优先型产品中技术更新周期较短的特点，运输时间的增加会导致笔记本电脑的上市时间延迟，一方面可能会被其他竞争企业抢占市场，削弱自身竞争力；另一方面则会导致消费者对等待产品丧失耐心，从而导致企业失去部分市场[13]。这些都可以归结为运输时间对货物自身价值的损失成本。依据市场调研与历史数据，笔记本电脑的运输总时间在10 d之内对于其自身价值不会造成影响，随着时间的增大，会使自身价值逐渐降低，但是随着市场与消费者自身心理预期的稳定，40 d之后不再下降。由于本文仅研究运输总时间对笔记本电脑价值的影响，对于以后较长时间内笔记本电脑价值的变化不做考虑。由此可以得出货物时间价值成本的另一组成部分，即运输总时间对货物自身价值造成的损失成本。根据国内笔记本电脑统计数据得出货物自身价值损失成本函数如下：

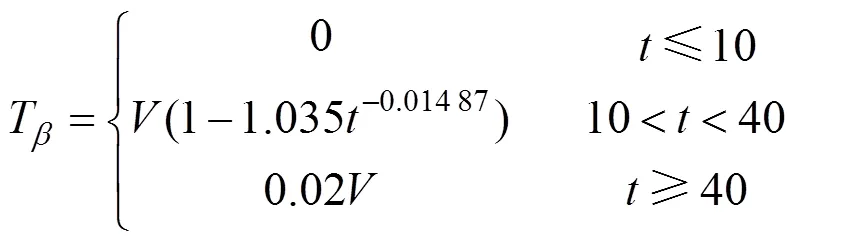
其中：为货物自身价值损失成本；为货物的总价值；为运输总时间，d。综上所述本文得出货物时间价值成本模型：

2.2 综合物流成本路径选择优化模型

2.2.1 模型假设

1)只在节点处发生运输方式的转换，且最多转换1次。

2) 每一种运输方式以FEU为单位，空运则根据每一40英尺集装箱所运输FEU笔记本电脑数量进行换算。

3) 公路与航空运输方式皆可随时出发，铁路及海运出发时间设置为每天的固定时刻，计算运费时不计入政府补贴运费。

4) 在运输方式转换过程中的短途运输采取公路运输。

2.2.2 符号说明

：运输终点；

2.2.3 目标函数

本文所定义的综合物流成本包含运输成本、运输方式转换成本、清关费用和时间价值成本4个 部分。

目标函数：

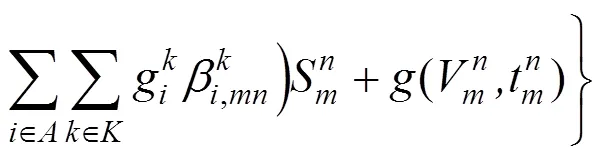
其中：

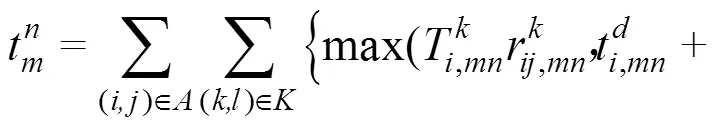
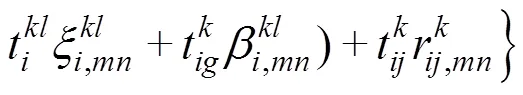
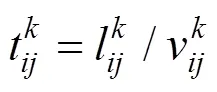
约束条件：

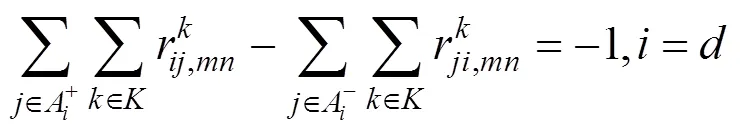
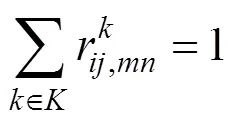
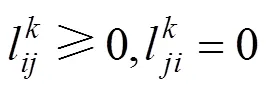
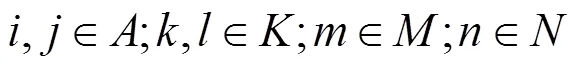
式(4)中表示产地的第档价值的笔记本电脑出口至欧盟的最低综合物流成本，式(5)表示产地的第档价值的笔记本电脑的运输总时间，式(6)表示从地经第种运输方式到地的运输时间，约束中式(7)~(9)表示产地的第档价值的笔记本电脑运输到终点都有且仅有一个完整路径，式(10)表示产地的第档价值的笔记本电脑从地到地仅有一种运输方式，式(11)表示产地的第档价值的笔记本电脑在地有且仅有一种方式清关，式(12)表示产地的第档价值的笔记本电脑在地运输方式最多转换1次，式(13)表示货物运输不会发生折返，式(14)表示其他条件。

3 模型求解

3.1 网络变形

为使运输网络图清晰明了，便于求解，本文将多式联运网络进行扩展变形[4]，假设每对相邻的节点之间都有种运输方式可供选择，可将每对相邻节点的后者扩展成个新节点，这个新节点与其前一个相邻节点之间的连线代表一种运输方式，由同一个节点扩展来的新节点之间不存在连接弧，原来有弧连接的2个节点，经扩展后得到的个节点之间两两有弧连接，原来没有弧连接的2个节点经扩展后得到的个新节点之间没有弧连接，同时，对于终点，扩展后的多个终点作为网络中的运输节点，最后再增加一个虚拟节点来代替终点，对新终点与原终点扩展得到的运输节点之间都只有1条弧相连，并且这些弧上的时间权重和费用权重全为0，弧上的运输能力为无穷大，如图2所示的一个简单的运输网络。

图2 简单网络图

图2是一个简单的网络图，由3个节点和3条弧组成，其中1到2和2到3之间的弧代表多种运输方式的路径，而1到3则表示经过节点较少的单一运输方式(空运)。经过网络变形后得到图3。

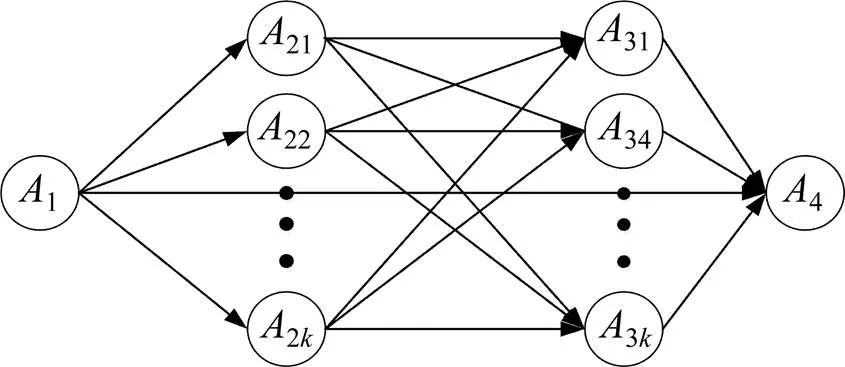
图3 变形后的网络图

图3中，2k表示由2扩展来的第个新节点，下标表示由1到2的第运输方式，1与2之间各运输方式的时间与成本加在2k相应的前向弧上；3k表示由3扩展而来的虚拟节点，下标表示由2到3的第运输方式，2与3之间各运输方式的时间与成本加在3k相应的前向弧上，后向弧的时间和成本都为0；4表示新增加的虚拟终点，网络变形后，把在节点处发生运输方式转换的转换成本和转换时间合并到相应的弧上，如从1到2选择第1种运输方式、2到3选择第3种运输方式，则在2处由第1种运输方式转换到第3种运输方式的转换成本和转换时间，则合并到弧(21,33)上，如果进行了通关，则加上清关费用和时间，而整个运输过程由扩展后的网络表示就是：(1,21,33,4)。

3.2 变形后的网络求解

经过上述的处理变化，本文所研究的问题就变成了一个求综合物流成本最小的类似最短路的问题，将运输成本、转换成本和清关费用以及运输时间、换装时间、清关时间合并到相应的弧上，同时考虑到本文所提出的时间价值成本模型是非线性数学模型以及所研究问题的特殊性，需要计算整个运输路径的时间价值成本。首先对原有网络进行网络变形，然后采用深度遍历搜索的算法求解本问题。具体如下：第档的笔记本电脑从起点o出发，先访问o，并将其标记为已访问过，然后从o出发，访问与其邻接且未被标记的节点，并将其标记为已经访问，接着从节点出发访问，重复这一过程直至终点，并记录其路径和综合物流成本，然后与下一条路径进行比较，保留综合物流成本较低的那一个，直至访问完节点出发所有的有路径。然后回溯到起点o，并且再选择一个与o邻接且未被标记的点进行上一过程，直至所有与起点o邻接的点出发的全部路径都已被访问为止，这样就得出了每个产地所有品级笔记本电脑的最优路径和最低综合物流成本。

4 案例分析

4.1 案例描述

以深圳和昆山2个笔记本电脑产地对欧洲出口为例，其基本情况如表1所示。在考虑时间价值成本的前提下将2个产地的不同品级的笔记本电脑以综合物流成本最低为目标，通过多式联运的方式出口至汉堡，并选出最优的运输方式和运输路线。海运班轮、铁路运输火车有固定的出发时刻，公路运输和空运皆随时出发。

表1 各产地笔记本电脑情况表

图1经网络扩展变形之后得到的虚拟运输网络图如图4所示，1和2点表示深圳、昆山，节点3和4由重庆扩展而来，记为重庆(3,4)，虚拟运输网络图中的节点与原网络图中的节点之间的关系为成都(5,6)，武汉(7,8)，苏州(9,10)，郑州(11,12)，上海(13,14)，深圳(15,16)，杜伊斯堡(17)，罗兹(18)，帕尔杜比采(19)，华沙(20)，(21,22,23,24,25,26,27,28, 30,31)为由汉堡扩充而来的虚拟节点，32表示虚拟终点。

4.2 结果分析

经过计算求解，在考虑时间价值成本的前提下各品级电脑分别从深圳和昆山出发运输到汉堡，得出了最优路径和和相应的最低综合物流成本，同时为了便于比较，同时给出了三大运输通道的最低物流成本，如表2和表3所示。

图4 虚拟运输网络图

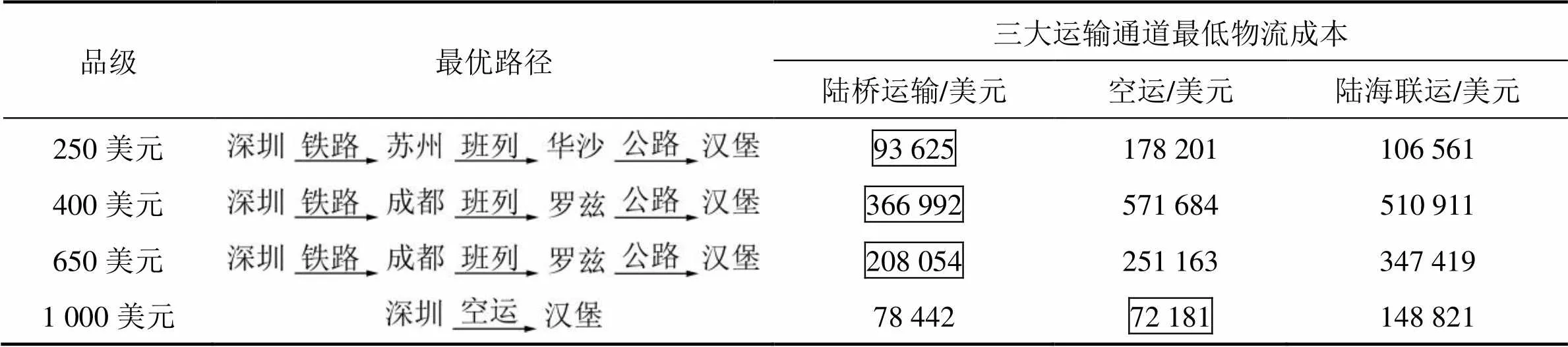
表2 最优路径和三大通道最低综合物流成本表(深圳)

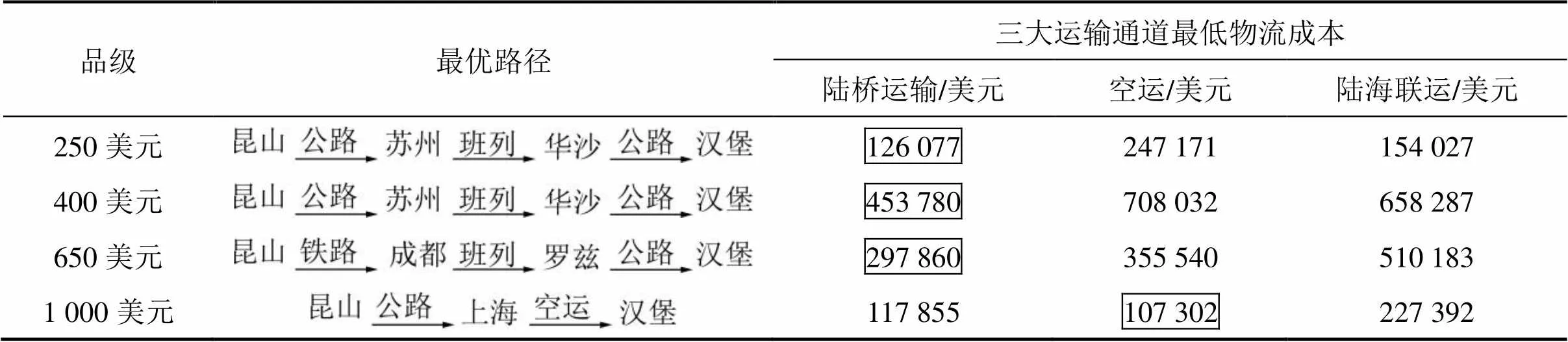
表3 最优路径和三大通道最低综合物流成本表(昆山)

从表2~3可以看出，深圳至汉堡笔记本电脑前3个品级运输的最优路径为经陆桥运输，最低综合物流成本为相应的陆桥运输费用，1 000美元品级为空运，最低综合物流成本为相应的空运费用，昆山至汉堡与此类似。在国内外短途运输时，选择都是公路运输，显示了公路在短途运输上的优势；从运输路线的选择来看，从中国到欧洲的大通道多是以中欧班列为基础的陆桥运输，由于深圳在空间上与本文涉及的5条班列各起始地的距离都相近，从其路线选择表明中欧班列(苏州—华沙)和中欧班列(成都—罗兹)在运输高价值商品时有优势；此外空运在运输极高价值的笔记本电脑具有优势。

4.3 价值变化对路径选择的影响

本文接着探究笔记本电脑价值(单价)的变化对路径选择的影响，假设笔记本电脑价值的变化是连续的且符合时间价值成本模型，本文以从深圳和昆山运输1 FEU笔记本电脑(空运时运输相同的数量)至汉堡所产生的综合物流成本为例进行研究，随着笔记本电脑价值的变化，相对应最低综合物流成本和最优路径也会产生变化，深圳、昆山两地笔记本电脑价值变化对路径选择的影响如图5~6。路径变化时的笔记本电脑价值和综合物流成本在图中标注，如图5，当价值超过206.5美元时，由海运转为陆桥运输。从图5~6可以看出，价值变化对海运影响最大，陆桥运输次之，空运最小。结果表明，以中欧班列为基础的陆桥运输和空运更加适合笔记本电脑这一类高价值、高时效商品，在高价值货源方面具有较高吸引力。

图5 价值变化对路径选择的影响(深圳)

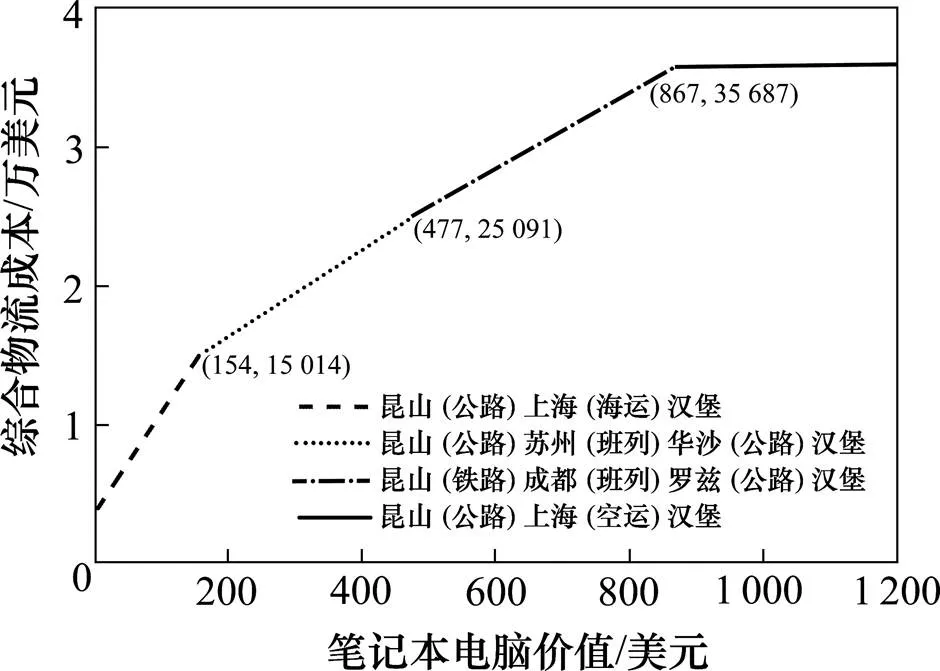
图6 价值变化对路径选择的影响(昆山)

5 结论

1) 本文站在生产企业的角度、从中欧运输现状出发对中欧之间的笔记本电脑运输进行研究，先建立时间价值成本模型，然后在此基础上建立以综合物流成本最低为目标的路径选择优化模型，然后进行网络变形并采用深度优先搜索算法进行求解。

2) 通过对路径选择结果和价值变化对路径选择的影响的分析，得出中欧班列和空运在运输高价值信息产品具有优势，其中中欧班列(苏州—华沙)和中欧班列(成都—罗兹)2条线路优势更为明显的结论。班列与空运应通过确定腹地货源特点，从时效性和经济性来突出自身的竞争优势。

[1] 李博. 基于多式联运的货物集装箱运输网络优化研究[D]. 北京: 华北电力大学, 2016. LI Bo. Research on transportation networks optimization of cargo containers based on multimodal transport[D]. Beijing: North China Electric Power University, 2016.

[2] 杨洋, 王汝英. 基于遗传算法的煤炭运输多式联运路径选择[J]. 物流技术, 2015, 34(8): 116−120. YANG Yang, WANG Ruying. Study on path selection in inter-modal coal transportation based on genetic algorithm[J]. Logistics Technology, 2015, 34(8): 116− 120.

[3] 杨文东, 王文芳. 有时间窗的多式联运问题分析与建模[J]. 南京航空航天大学学报, 2009, 41(1): 111−115. YANG Wendong, WANG Wenfang. Analyzing and modeling of multimodal transportation with time window[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2009, 41(1): 111−115.

[4] 王清斌, 韩增霞, 计明军, 等. 基于节点作业随机特征的集装箱多式联运路径优化[J]. 交通运输工程与信息, 2011, 11(6): 177−144. WANG Qingbin, HAN Zengxia, JI Mingjun, et al. Path optimization of container multimodal transportation based on node operation randomness[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(6): 177−144.

[5] 张小龙, 陈小鸿. 混合时间窗约束下多目标多式联运路径优化研究[J]. 综合运输, 2018, 40(8): 98−104. ZHANG Xiaolong, CHEN Xiaohong. Study on multiple- objective multimodal transport path optimization under mixed time windows[J]. China Transportation Review, 2018, 40(8): 98−104.

[6] 吴晓莉,马华伟.多式联运环境下带时间窗的多产品运输问题研究[J]. 物流工程与管理, 2014, 36(239): 74−77. WU Xiaoli, MA Huawei. A multi-product transportation problem with time windows research in the multimodal transportation environment[J]. Logistics Technology, 2014, 36(239): 74−77.

[7] ZHANG Fengli, Johnson Dana M, WANG Jinjiang. Integrating multimodal transport into forest-delivered biofuel supply chain design[J].Renewable Energy, 2016, 93(2): 58−67.

[8] GUO Zhaoxia, ZHANG Dongqing, LIU Haitao. Green transportation scheduling with pickup time and transport mode selections using a novel multi-objective memetic optimization approach[J]. Transportation Research Part D, 2018, 60(5): 137−152.

[9] HAO Congli, YUE Yixiang. Optimization on combination of transport routes and modes on dynamic programming for a container multimodal transport system[J]. Procedia Engineering, 2016, 137(1): 382−390.

[10] 王姣娥, 景悦, 王成金. “中欧班列”运输组织策略研究[J]. 中国科学院院刊, 2017, 32(4): 370−376. WANG Jiao’e, JING Yue, WANG Chengjin. Study on better organization of China-Europe express train[J]. Bulletin of Chinese Academy of Sciences, 2017, 32(4): 370−376.

[11] 王杨堃. 中欧班列发展现状、问题及建议[J]. 综合运输, 2015, 37(增1): 70−76. WANG Yangkun. Status, problems and suggestions on development of Sino-Europe block trains[J]. China Transportation Review, 2015, 37(Suppl 1):70−76.

[12] 付新平, 张雪, 邹敏, 等. 基于价值量模型的中欧班列经济性比较分析[J]. 铁道运输与经济, 2016, 38(11): 1−6. FU Xinping, ZHANG Xue, ZOU Min, et al. Analysis on economics of China-Europe block trains based on the value model[J]. Railway Transport and Economy, 2016, 38(11): 1−6.

[13] 秦欢欢, 秦胜, 郑平标. 基于货物价值的中欧班列目标货源分析[J]. 铁道货运, 2016, 34(87): 13−20. QIN Huanhuan, QIN Sheng, ZHENG Pingbiao. Analysis of supply of goods for China-Europe block train based on freight value[J]. Railway Freight Transport, 2016, 34(87): 13−20.

[14] 李玉民, 郭晓燕, 杨露. 考虑多目标的中欧集装箱多式联运路径选择[J]. 铁道科学与工程学报, 2017, 14(10): 2239−2248. LI Yumin, GUO Xiaoyan, YANG Lu. Route optimization of China-EU container multimodal transport considering various factors[J]. Journal of Railway Science and Engineering, 2017, 14(10): 2239−2248.

[15] Seo Young Joon, CHEN Feilong, Roh Sae Yeon. Multimodal transportation: The case of laptop from Chongqing in China to Rotterdam in Europe[J]. The Asian Journal of Shipping and Logistics, 2017, 33(3): 155−165.

Study on the route optimization of China-Europe laptop multimodal transport considering time value cost

LIU Chang, GUAN Xiuting, ZHANG Jinwei, JI Mingjun

(Dalian Maritime University, College of Transportation Engineering, Dalian 112026, China)

A time value cost model was established for laptop’s characteristics of high timeliness and high value, simultaneously considering multi-origin and multi-grade, an optimization model of multimodal route selection aiming at the lowest comprehensive logistics cost was established, transportation network of model was transformed by adding virtual nodes, and then a depth-first search algorithm was used to solve the route selection optimization model. The export case of laptop between China and Europe shows that compared with sea transport, land-bridge transport and air transport have lower comprehensive logistics costs in transportation of laptop. Finally, the influence of value change on route selection was explored, it provided reference for trade transportation between China and Europe.

time value cost; multimodal transport; route optimization; China Railway Express; laptop transport

U116.2

A

1672 − 7029(2019)09− 2352 − 08

10.19713/j.cnki.43−1423/u.2019.09.030

2018−12−24

国家自然科学基金资助项目(71572022)；辽宁省“百千万人才工程”经费资助项目(2016236)；中央高校基本科研业务费专项资金资助项目(312016301)

计明军(1973−)，男，蒙古族，内蒙古赤峰人，教授，博士，从事物流与供应链管理研究；E−mail：jmj@dlmu.edu.cn

(编辑 阳丽霞)