结构-地基系统高阶时域模型的动输入方法

周文凯 陈灯红

(1.三峡大学 土木与建筑学院,湖北 宜昌 443002;2.三峡大学 期刊社,湖北 宜昌 443002)

结构-地基动力相互作用是结构动力分析及结构抗震计算中的一个重要方面.研究结构-地基动力相互作用问题时,为考虑无限地基的辐射阻尼效应,最理想的做法是将地基范围取得足够大.由于动力分析中,网格尺寸通常受到最小波长的限制,这样势必会要求很大的计算机存储量和工作量,实现时代价很大.因此,通常情况下在无限的地基中截断一定范围,这样该系统分为近场的有限域和远场的无限域部分.有限域一般采用有限元法考虑,如何准确地模拟无限域的辐射边界条件是研究的难点.基于各种计算假设和不同的数学、力学模型,许多学者建立了多种人工边界条件,它们可分为两类,即局部的近似边界和全局的精确边界.近似边界包括黏性边界(viscous boundary)[1]、黏弹性边界(viscous-spring boundary)[2-3]、多次透射公式(multi-transmitting formula)[4]、无限元(infinite element)[5]等;精确方法包括边界元法(BEM)[6]、比例边界有限元法(SBFEM)[7-8]等.

在动输入方面,一般而言,有作为封闭系统的振动体系和作为开放系统的波动体系两种方式.对于封闭系统,将结构的惯性力作为外力输入,目前一般工业和民用建筑物多采用这种输入方式.然而,对于尺寸、质量很大,空间效应显著的高坝结构,传统的无质量地基假定不符合实际[9],地基的惯性和阻尼不能忽略,其动力学方程必须作为开放系统的波动问题来求解.

比例边界有限元法是由 Wolf、Song于20世纪90年代提出的一种半解析数值方法.该方法在发展之初是为了解决无限域中的波动传播问题,并具有显著的优势.近年来,Song、Bazyar提出分别采用Pade近似[10]和连分式方法[11]来求解无限域的动力刚度矩阵,这两种近似算法具有收敛范围广、收敛速度快等优点,在不影响计算精度前提下其计算效率比早期的卷积积分算法有明显提高.Birk等[12]针对多自由度系统高阶连分式展开时可能造成刚度矩阵病态的问题,改进了文献[11]中的连分式算法,算例表明改进后的算法明显提高了数值稳定性和鲁棒性.陈灯红等[13]在文献[12]的基础上发展了一种大坝-地基动力相互作用的高阶时域模型.

本文在文献[13]的研究成果基础上,在时域里建立了一种结构-地基相互作用的高阶模型,借鉴黏弹性人工边界等效力的动输入方法[14-15],建立了与上述高阶时域算法相匹配的波动输入模型,并通过两个数值算例验证了文中建立方法的有效性.

1 SBFEM位移控制方程

基于弹性动力学基本方程,采用比例边界坐标(ξ为径向,η为环向)变换,文献[8]详细地推导出了SBFEM位移控制方程为:

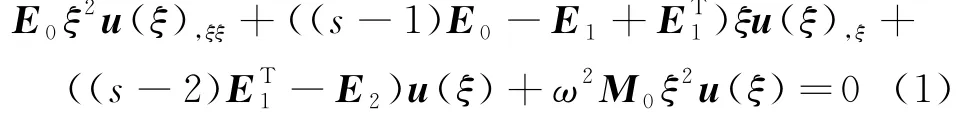
其中,s为空间维数,s=2或3分别表示二维或三维情况;u(ξ)为待求的位移向量.二维情况下,4个系数矩阵E0、E1、E2、M0分别表示为

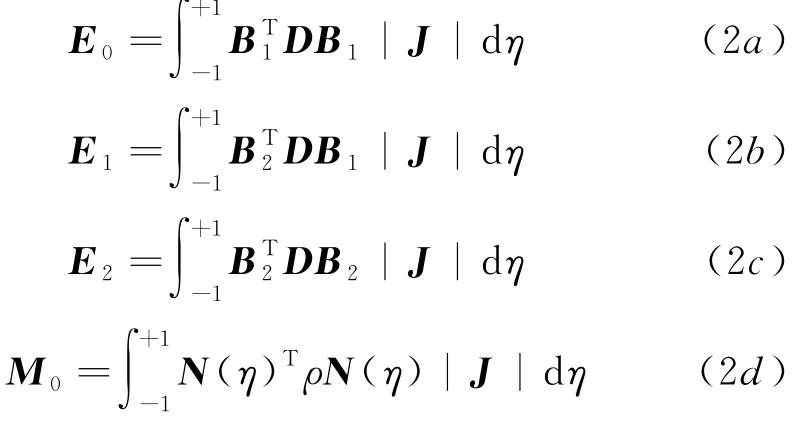
式中,B1、B2为应变-位移矩阵;D为弹性矩阵;J为ξ=1边界上的Jacobian矩阵;N(η)为形函数;ρ为质量密度.

2 高阶时域算法

2.1 近场有限域

结构-地基系统的动力相互作用示意如图1所示,近场有限域动力学方程可表示为

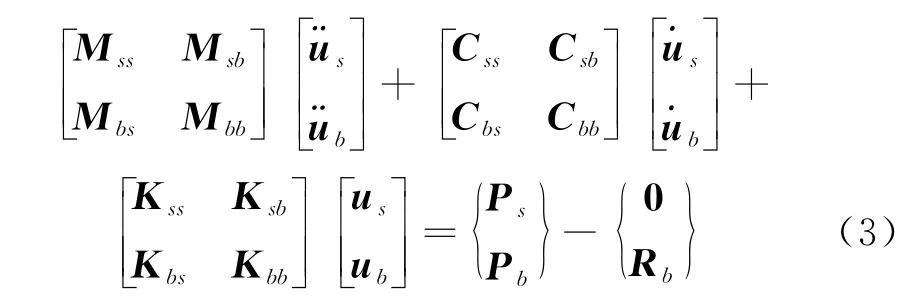
式中,M、C、K分别表示有限域的质量矩阵、阻尼矩阵和刚度矩阵;下标s、b分别为结构除交界面以外的自由度和结构-地基交界面上的自由度;Ps、Pb、Rb分别为结构所受外力、地基所受外力、结构-地基系统的相互作用力.

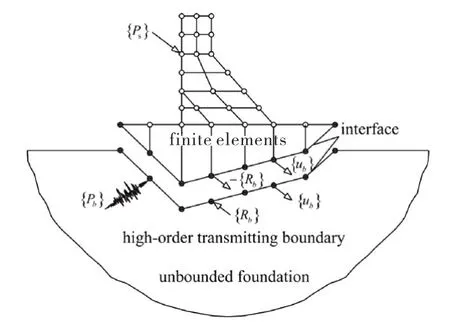
图1 土-结构相互作用系统

2.2 结构-地基耦合系统的运动方程

将以u(ξ)为未知量的二阶偏微分方程式(1)转化为以无限域动力刚度矩阵S∞(ω)为未知量的比例边界有限元控制方程,然后将S∞(ω)采用连分式展开求解[13,16],根据边界ξ=1上的力-位移平衡条件,建立了无限域时域分析的边界条件,即

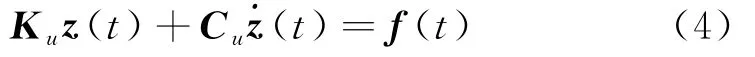
将近场有限域和远场无限域通过结构-地基交界面上的相互作用力向量Rb(如图1)进行耦合[13,17].对于线性系统,联合式(3)、(4),并按照自由度顺序对应相加并展开,得到结构-地基耦合系统的动力学方程为:

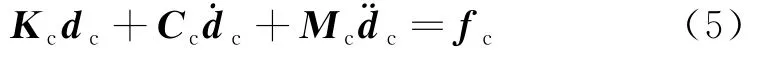
其中,耦合系统的刚度、阻尼、质量矩阵Kc、Cc、Mc,以及待求向量dc、荷载向量fc分别表示为

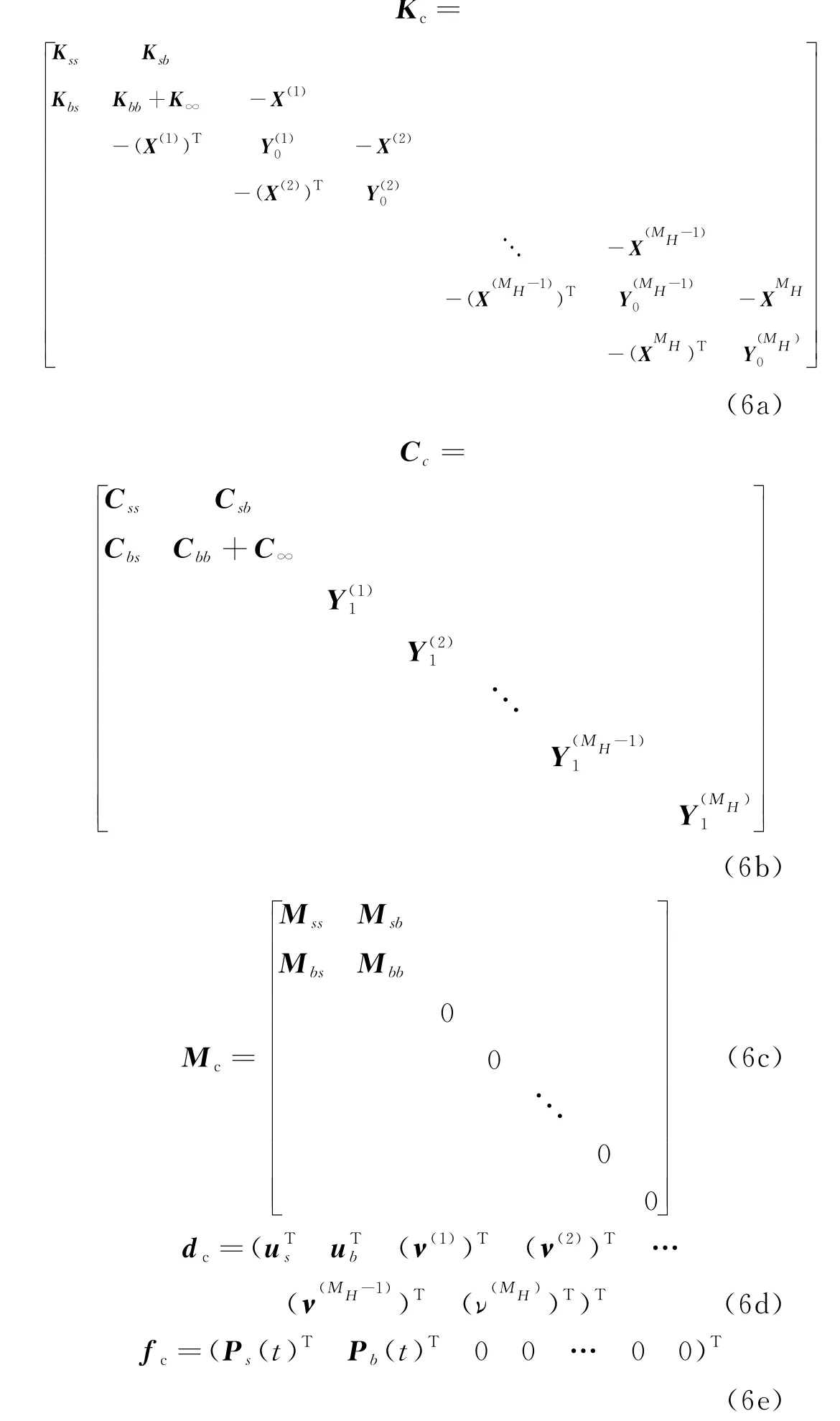
从上式可以看出,耦合系统的刚度矩阵由K∞及高阶项(阶数i=1,2,…,M H)组成,阻尼矩阵由C∞及高阶项组成,该式即为高阶边界条件.若上式中i=0,则边界条件退化为刚度为K∞、阻尼为C∞的弹簧-阻尼器单元,即黏弹性边界,其只有一阶精度.

3 动输入方法

由式(4)可看出,该边界实质上是由若干弹簧-阻尼器并联组成的高阶边界条件,其性质与黏弹性人工边界相似,能够吸收由近场有限域向远场无限域散射的外行波.针对外源波动输入问题时,需要在人工边界处施加自由场荷载,则人工边界上节点的等效荷载为

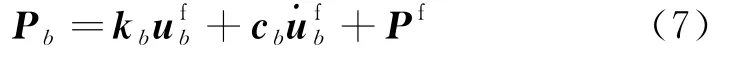
式中,kb、cb分别为式(4)中表示无限域刚度矩阵Ku、阻尼矩阵Cu的子矩阵;分别为自由场位移和速度矢量;Pf为自由场应力矢量,可根据下式计算得到

其中,l、m为边界外法线的方向余弦;应力σ可由弹性理论求得,即

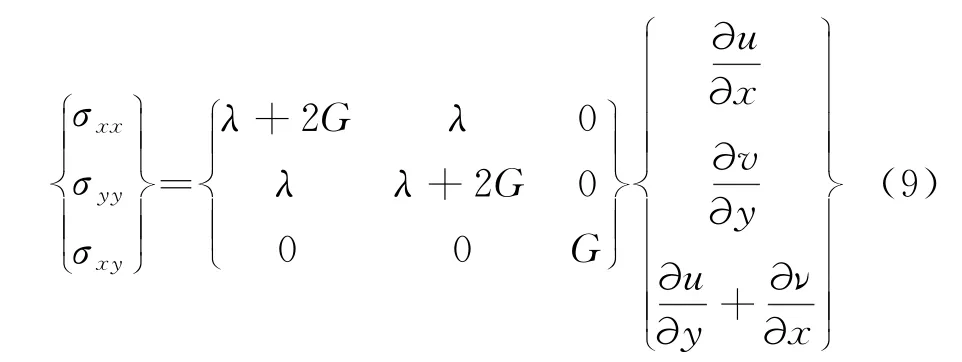
式中,λ、G为 Lame常数,并有ρ为介质的质量密度,cs、cp分别为剪切波、膨胀波的波速.

当从底部边界垂直入射P波时,底部的边界条件为u=0,ν=ν0(t),则在高度h处,自由场位移、速度可表示为入射波和反射波的叠加,即

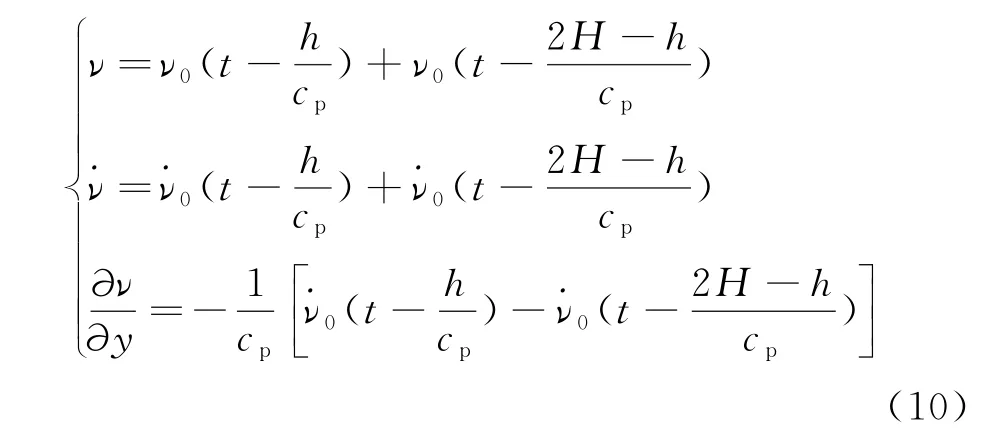
式中,H为底部边界到自由表面的距离.

对于底部边界,其边界条件为h=0,{l,m}T={0,-1}T,将式(8)～(10)代入式(7)中,等效荷载Pb可表示为

当从底边界垂直入射SV波时,底部的边界条件为u=u0(t),ν=0,则等效荷载Pb计算为

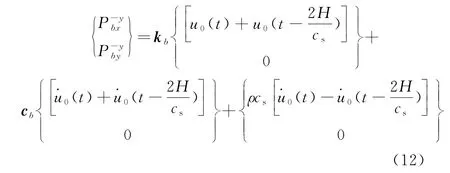
对于左、右两侧边界的等效荷载Pb也可按类似的方法求出.

4 数值算例

4.1 算例1

本文涉及到高阶时域算法和波动输入方法两个关键问题,首先为了验证高阶时域算法的正确性,考虑如图2所示的相互作用问题,取e=b=1.近场有限域、远场无限域地基的材料参数分别取为G1=4G=4,ρ1=ρ=1,ν1=0.25;G2=G=1,ρ2=ρ=1,ν2=0.25.施加在顶部自由面上的均布荷载P(t)如图3所示.

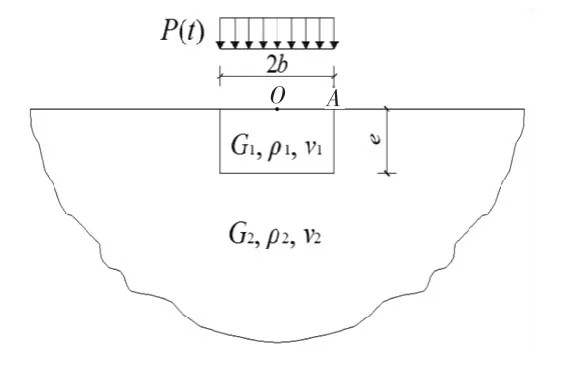
图2 耦合系统

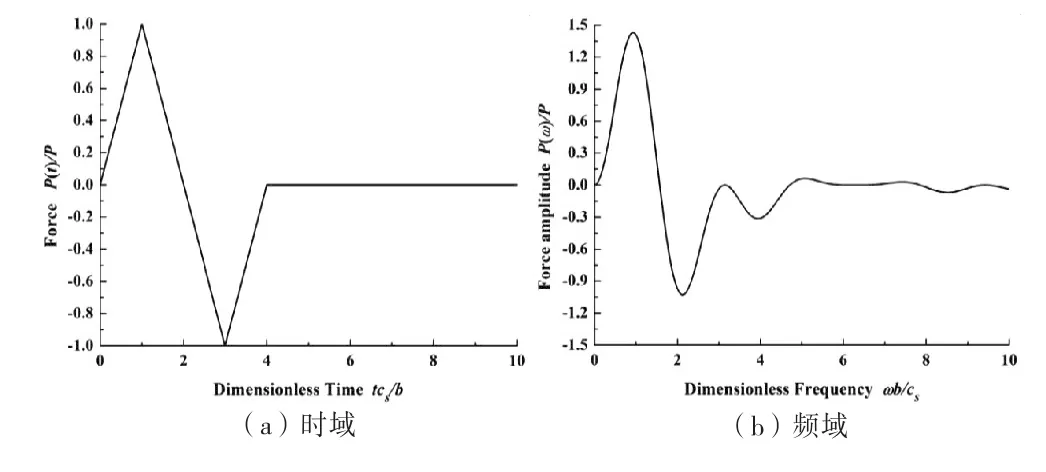
图3 施加的均布荷载

本文算法中,耦合系统采用四结点四边形单元离散,划分72个四结点单元,共91个结点,其中截断边界采用24个两结点线单元离散,相似中心选在O点,如图4所示.计算总时间为20b/cs,积分步长为t=0.02b/cs.

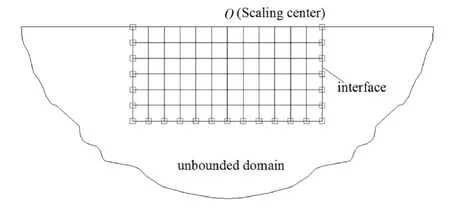
图4 耦合系统的网格图

为了说明本文算法的精确性,采用有限元扩展网格进行了对比分析.扩展网格的计算区域大小取为对称的20b×20b,采用八结点四边形单元离散,划分了6 400个单元共19 521个结点,该模型中截断边界采用固定边界条件.

为了对比说明本文算法的优势,同时进行了有限元法结合黏弹性边界对该问题的分析[18].计算区域取为4b×2b,有限元网格采用八结点四边形单元离散,划分了288个单元共937个结点.

图5为观测点O、A点的无量纲竖向位移时程.由图5可知,本方法(M H=6)的结果与有限元扩展网格的结果在无量纲时间5～10 s之间略有偏移;当M H增大到8时,两者吻合得很好;而黏弹性边界在无量纲时间5～10 s之间偏移较大,需要进一步扩大计算范围才能提高计算精度.

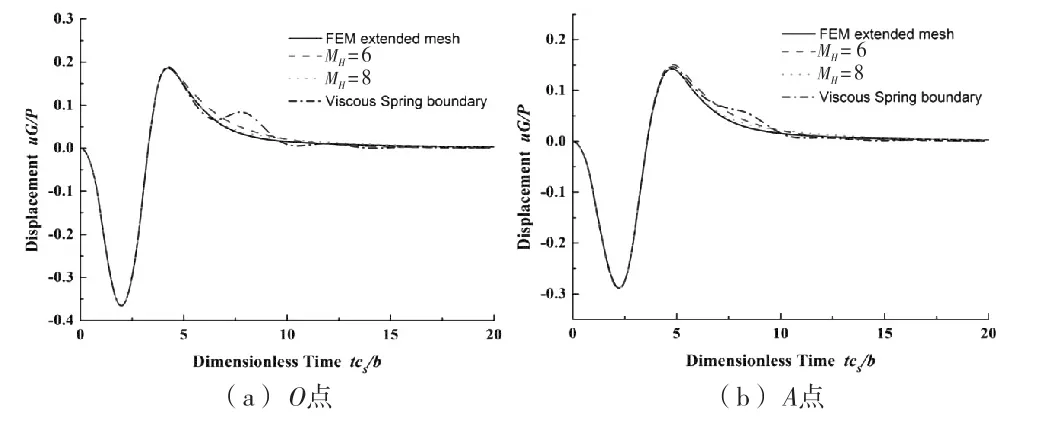
图5 O、A点竖向位移时程

4.2 算例2

其次,为验证上述波动输入法的正确性,采用底部垂直入射SV波的均匀弹性半空间进行验证.介质的力学参数为:弹模E=13 230 MPa,泊松比ν=0.25,密度ρ=2 700 kg/m3,波速cs=1 400 m/s,cp=2 425 m/s,入射波的位移方程为:

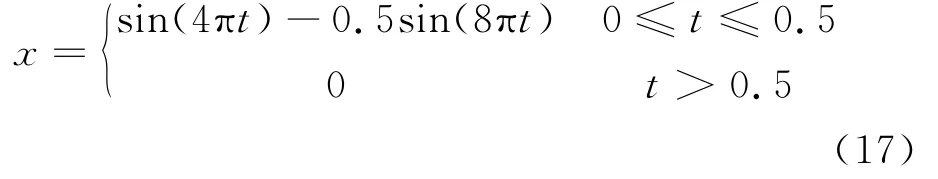
计算区域的范围为762 m×381 m,有限元单元尺寸为15.4 m×15.4 m,单元数为450,其中截断边界采用60个两结点线单元离散,结点数为496.计算总时间为2 s,时间步长取为0.01 s.经过计算得到系统顶部和底部各点的水平向位移时程,如图6所示.

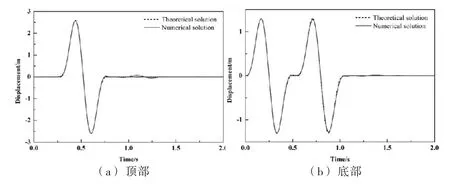
图6 水平向位移时程

可以看出:顶部自由表面的最大值(t=0.544 s)为入射SV波幅值的2倍;底部位移时程的前半段(t≤0.544 s)是入射波引起的位移,后半段(0.544 s≤t≤1.089 s)是反射波引起的位移.上述数值解与理论解吻合良好,从而说明本文建立的高阶算法及其动输入方法是正确的、精确的.

5 结 语

采用有限元法模拟有限域,采用基于SBFEM的高阶透射边界模拟远场无限域,构建了一种结构-地基动力相互作用的高阶时域模型及相适配的动输入机制.借鉴黏弹性人工边界中等效力的动输入机制,将截断边界上的总波场分解为散射场和自由场,其中局部场地效应引起的散射场由高阶人工边界条件自动满足,无局部场地效应影响的自由场由弹性理论求出.通过两个数值算例验证了建立的高阶时域模型及相应的动输入机制的正确性、精确性,为复杂结构的地震动输入奠定基础.