基于TESAOC的ARIMA-BP组合模型在混凝土坝变形预测中的应用

王 成 胡军然 徐平波 黎大鹏 祖安君

(1.中交四航工程研究院有限公司,广州 510230;2.河海大学 水利水电学院,南京 210098)

混凝土坝变形效应量是坝体结构安全性态的综合表现,坝工界普遍将其作为最主要的监测量.因此,有必要建立恰当的变形监控模型,对混凝土坝工作性态进行准确地预测预报.近年来,国内外学者对混凝土坝变形监测预测模型的研究越来越深入,逐步回归模型、神经网络模型、支持向量机模型等[1-3]一些新的理论和方法不断被引入到该领域中.但是混凝土坝的监测量受多种因素的共同影响[4],这些单一预测模型的建立所考虑的因素相对片面,存在较大的局限性,往往不能全面揭示混凝土坝监测量的内在规律,预测精度仍有提高的空间.

基于最优加权法的组合预测模型[5],虽然提高了预测的精度,但模型中权重大小是固定的,不随时间的推移发生改变.事实上,由于混凝土坝的变形处于一种复杂的动态系统中,其变形的各种影响因素在整体变形过程中的权重大小也是动态变化的.因此,组合模型的权重确定方法仍然需要进一步改进.戴明远在《基础信息论》中提出了“远小近大”的观点[6],即越是最近产生的数据,其中包含的有用信息就越多.结合以上观点,本文对传统的模型权重确定方法进行了改进.首先引入移动算术平均法,通过试算找出最佳建模的移动样本数,降低数据突变的不利影响;其次在模型权重的计算方法中融入时效函数,实现权系数的动态化,实现对混凝土坝监测量的动态预测;最后针对单一模型误差对组合模型预测误差的影响,引入模糊补偿的方法,进一步控制模型权系数的自适应,得到最佳的模型权系数.结合上述3种方法,最终建立了基于时效函数的自适应优化组合预测模型.工程实例表明,改进的预测模型具有良好的预测效果.

1 组合预测方法

设对某一具体对象有n种不同的预测方法,该物理量的N个实际观测值为Y t(t=1,2,…,N),记组合预测方法的加权系数向量为其中k i为第i种预测方法在组合时对应的权重,设第i种预测方法的预测值为y it,则组合预测模型的预测值y t为:

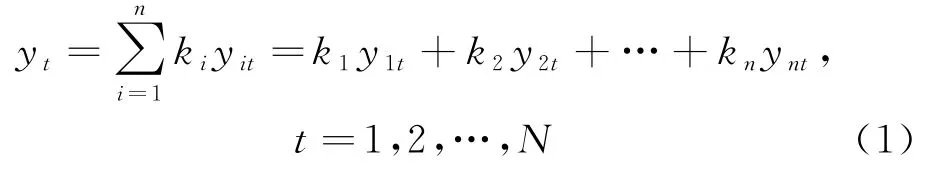
1.1 最优加权组合预测原理

最优加权组合预测法以所有单一模型的误差平方和最小为出发点,采用线性规划的方法求出单一预测模型的权重,再进行加权组合得到组合预测模型.其具体原理如下:

设第i种预测模型的预测误差为e it=y it-Y t,则组合预测模型的预测误差为组合预测模型的预测误差平方和

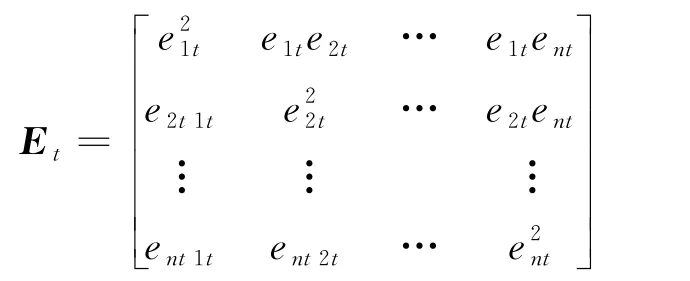
则模型权重的求解转化为以下数学规划问题:

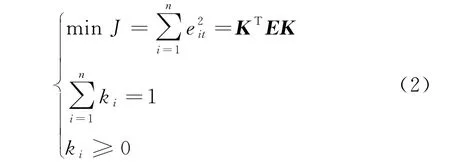
式中,E为误差信息矩阵,

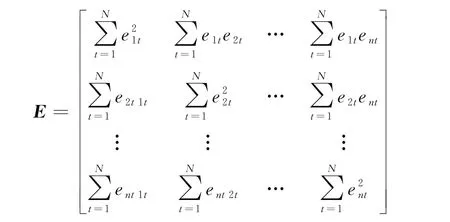
1.2 TESAOC法

1.2.1 最优加权法的局限性

最优加权法可以求出组合模型中的最佳组合权系数,一定程度上提高了预测精度,但由于权系数固定,在混凝土坝位移预测中仍存在以下不足:

1)混凝土坝的位移受到多种因素的共同作用,且某些作用因素具有明显的时效性,固定的权系数无法将作用因素的这一特点充分体现出来.

2)由于模型的局限性,不同的预测模型在不同的时间段预测效果不同,组合模型的预测精度自然也随着时间的变化而变化,而固定权系数无法与之匹配.

3)混凝土坝的变形观测资料是典型的时间序列,随着时间的推移,样本数一直在动态增加,因此模型的权系数也应该随时间动态变化,而固定权系数不具备这一特点.

1.2.2 TESAOC法预测原理

单一模型利用历史信息对研究目标变化规律进行拟合时,拟合的准确度很大程度上取决于历史信息的可用性,也就是数据质量,而精确性、时效性和一致性[7]构成了信息可用性的其中3个维度,精确性就是保证数据能够准确地描述对应的目标,时效性是保证数据与时俱进,不陈旧过时,一致性是保证数据在某些特定的约束下发展,不违背前设条件.只有保证了信息的这3个特性才能确保模型拟合的精确性,使得预测效果更贴近于实际情况.

混凝土坝一般要经历长达数年的施工期,蓄水期过后再转入漫长的运行期,因此混凝土坝的变形监测工作自然也需要经历一个很长的时间段,而在这个过程中产生的监测数据将不可避免地受到很多外在因素的影响,在一定程度上会丧失信息的可用性.因此,为了尽可能准确地描述和预测混凝土坝的运行状态,需想办法确保信息数据的精确性、时效性和一致性.

针对上述问题和需要,引入以下方法进行改进:

1)由于某些人为原因或仪器的损坏等,混凝土坝位移监测量会出现不同程度的突变,某些可以通过查看资料轻易剔除,某些则难以发现,导致监测数据与实际运行状况不相吻合,影响模型预测的效果.为此引入移动算术平均法来降低或消除突变的不利影响:

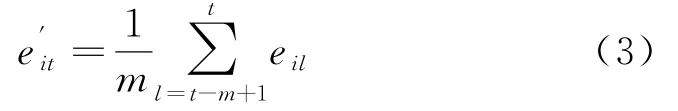
式中,m为移动算术平均法的样本数,具体的取值按照最小二乘法原理,通过试算方差T的值来确定,当方差T达到最小时对应的m值即为所求.方差T的公式如下:

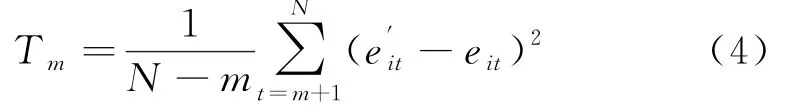
式中,N为观测值数.

2)数据时效性对模型的作用至关重要,而混凝土坝位移监测量显著的时效性特点,要求模型须精确模拟时效作用,为此引入移动样本[8]的方法,每次取目标值前m个时刻的样本历史值来计算权系数.同时根据信息论中“远小近大”的观点,为了突出历史数据重要性随时间的变化,在权重的确定公式中引入一个时间的增函数F(t),给不同时间产生的数据赋予不同的权重,随着时间的往后推移,数据的权重呈逐渐增大的趋势,即后一个数据的权重大于前一个数据的权重,以此实现预期的目标.融入时效函数的自适应优化组合(TESAOC)预测模型的权系数表达式为:

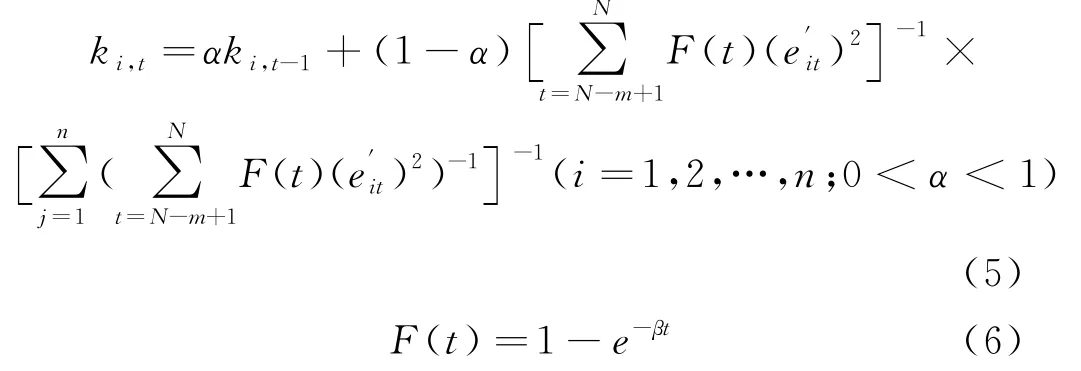
式中,m为移动样本数,具体的数值通过试算法求得;α为平滑系数,可取0.1～0.3;β为常系数,具体取值取决于监测样本随时间的变化情况;N为观测值数.

3)混凝土坝变形监测的模型预测值与实际观测值的偏差在2.5%之内的,可以说预测结果是准确的[9],此处根据实际偏差与允许偏差的大小关系,将模型的误差分为3类,即P(＞2.5%)、Z([-2.5%,2.5%])、N(＜-2.5%).

通过研究单一模型具体时刻的预测误差对组合模型预测误差的影响有:若t时刻的e t∈P且e it∈P,则t时刻的第i种单一模型会进一步扩大组合模型的预测误差,那么就需要采取措施来限制这种不利影响,可以采取减小该单一模型t+1时刻权系数的方法来实现.基于此,引入模糊补偿的方法,实现单一模型权系数的调整.在实际操作中会有9种情况出现,现列举其中3种及相应的解决措施如下:

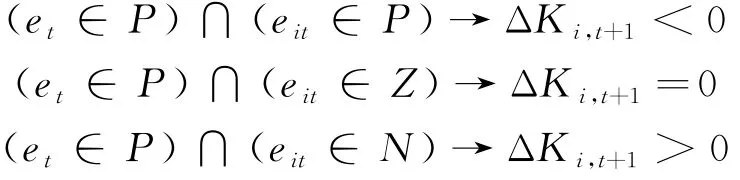
若某单一模型t时刻的偏差不符合要求,即预测偏差的绝对值大于2.5%,则可使t+1时刻的权系数朝着减小偏差的方向发展,可取为:

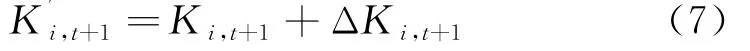
式中,ΔKi,t+1的值由中心平均模糊消除器[9]求出.

1.3 基于TESAOC法的ARIMA-BP组合预测模型

基于TESAOC混凝土坝变形组合预测模型建模步骤如下:

Step1:导入混凝土坝变形实测数据序列;

Step2:利用ARIMA模型和BP神经网络分别对数据序列建模,并得出各自的预测值;

Step3:试算所选样本方差,并利用最小二乘法求出移动算术平均的样本数m;

Step4:确定TESAOC预测模型的参数α、β;

Step5:利用两种单一模型的拟合值计算出初步权系数;

Step6:计算初步权系数下组合模型的拟合值,如果拟合偏差满足设定要求,则确定模型的最终权系数;若不满足,则对权系数进行模糊补偿;

Step7:建立基于TESAOC的混凝土坝变形组合预测模型,并对变形进行预测.

2 实例应用

以文献[5]工程应用中的某混凝土坝变形数据为例来验证本文所研究方法的可用性,同样将前92个数据用来拟合,后5个数据用来预测,具体的变形数据见表1.

首先分别利用ARIMA和BP神经网络两种单一模型对数据进行拟合与预测;然后采用最优加权组合原理计算出这两种模型的权重,得到的结果为KA=0.1,KB=0.9,继而算出相应的组合预测值;最后采用引入时效函数的自适应优化组合原理进行计算,经过中心平均模糊消除器的处理后,得到两个模型每个序列点处最终的权系数,从而实现对变形值的预测.4种模型预测值与实测值的对比情况见表2和图1,4种模型的误差平方和对比结果见表3.

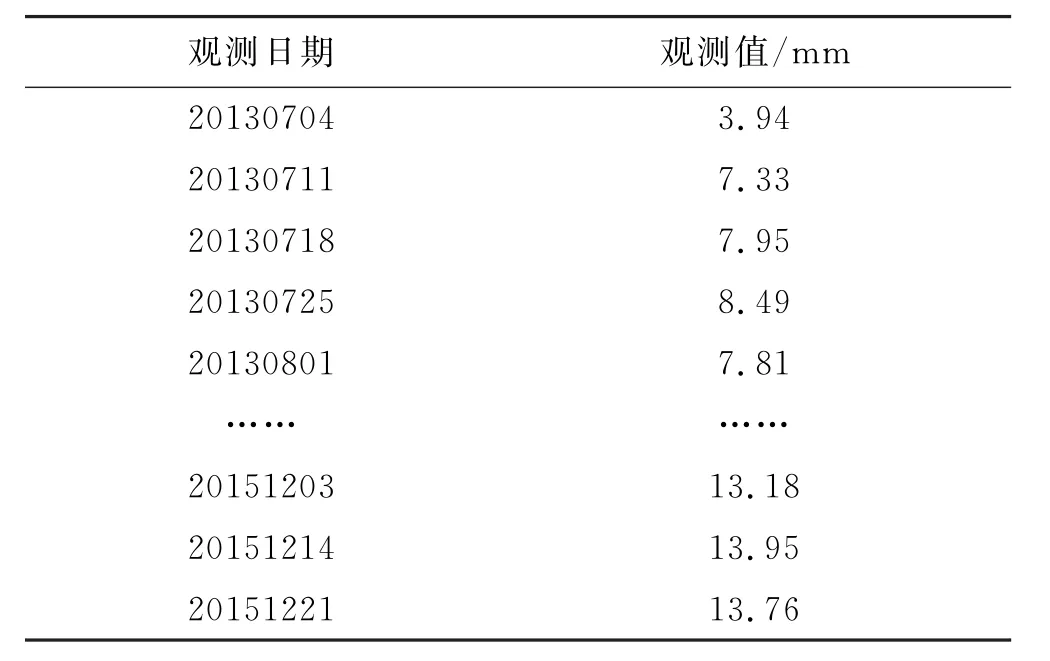
表1 坝顶某测点顺河向位移的历史观测值

表2 4种模型的预测值与相对误差

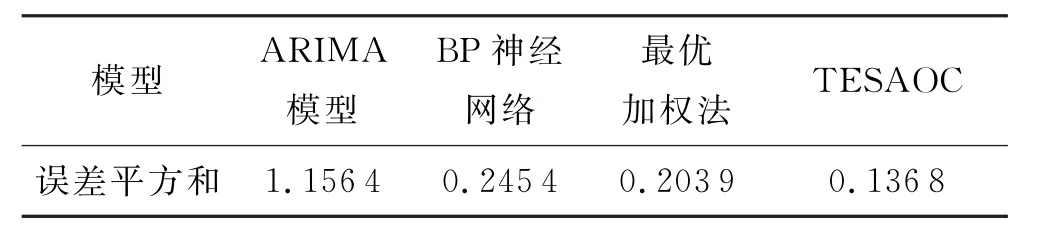
表3 模型误差平方和对比

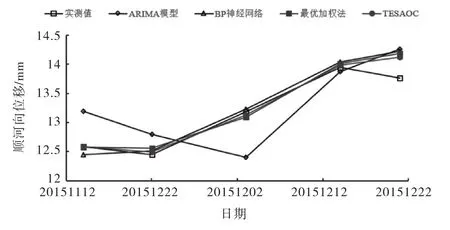
图1 4种模型预测值与实测值比较图

由表2、表3和图1的结果分析可知:融入时效函数的自适应优化方法的预测误差明显小于最优加权法,模型的误差平方和有了显著减小,预测值更接近于实测值,预测效果明显优于最优加权法,说明融入时效函数的自适应优化组合预测方法充分考虑了数据时效性的特点,引入的动态权系数更加吻合混凝土坝位移变化规律,而与最优加权法中不同时刻数据样本的权系数保持一致的不合理性相比,有了极大的进步和改进,在混凝土坝位移预测中有更好的适用性.

3 结 论

1)融入时效函数的自适应优化组合预测方法,同时引入了移动算术平均和模糊补偿的方法,充分考虑了模型权系数的时效性,从而得到各组合项的动态权系数,比最优加权法计算出来的结果更加全面准确.工程实例表明,该方法提高了模型的预测精度和稳定性,结果更接近于工程实际,在混凝土坝变形监控数据预测中具有较好的应用前景.

2)该模型在实际操作过程中是基于单一模型进行组合加权的,所以应努力提高单一模型的精度,精度低的模型不宜进行组合,须舍弃.此外,本文选取的时效函数只是简单的关于时间的增函数,没有联系到实际的混凝土坝运行情况,因此未来仍需要对时效函数的选择问题进行进一步的研究.