动车组制动夹钳悬吊刚度对频率响应特性的影响
2019-03-22曾梁彬孟永帅
曾梁彬,孟永帅
(中车戚墅堰机车车辆工艺研究所有限公司,江苏 常州 213011)
0 引言
随着我国高速动车组列车运营速度的不断提高,外部激扰频率增大,尤其在轨道不平顺、通过曲线、道岔和会车时,容易诱发列车走行部和车体在更宽频域范围内产生谐振或局部共振,严重影响列车运行的平稳性和安全性[1-3]。近年来,随着电动车组模式的普及,越来越多的设备悬挂安装在转向架上,一定程度上影响了车辆振动;轻量化技术的推广也导致车体整体刚度降低,加剧车体振动,直接影响乘坐舒适性[4]。
车辆在运行过程中承受的外部激扰主要通过一系、二系悬挂系统进行传递,并直接作用于车下设备;而设备自身的振动也会作为附加载荷反作用于车体[5-7]。因此,车体与车下设备耦合振动特性的研究已逐步成为研究热点。Sun等[8]研究了单一设备的悬挂静挠度对车辆平稳性的影响及主动控制方法。石怀龙等[9]基于动力吸振原理,建立多个车下设备和弹性车体在垂向上的耦合振动模型,研究不同设备悬挂频率、联接阻尼、质量和安装位置对车体振动分布的影响规律。贺小龙等[4]则在车辆-设备耦合振动模型中,重点考虑几何滤波效应,研究单级、双侧形式的悬挂方式及其悬挂参数对列车垂向振动的影响。吴会超等[10-13]对比刚性悬挂和弹性悬挂对降低车体垂向振动的作用,认为车下设备采用弹性悬挂更为合理,通过合理设计弹性悬挂的频率,使其接近车体模态频率时,能够有效降低车体垂向弹性振动;另外,弹性悬挂的各项刚度对各项振动的影响程度不同,可根据实际效果对悬挂的各项刚度进行独立设计。
以上各项研究的焦点都集中于车下设备对车体振动的影响,且分析模型中多将车下设备简化为等效质量,而对车下设备自身振动方面的研究鲜有报道。若车下设备的自身振动得不到有效控制,可能进一步加剧车体振动。因此,选取安装于转向架上的制动夹钳单元作为研究对象,基于模态分析与振型叠加,建立制动夹钳单元的振动模型,重点分析悬吊刚度对制动夹钳自身频率响应特性的影响。
1 基于频率响应的振动分析模型
1.1 制动夹钳单元结构
动车组用某型三点吊挂式制动夹钳单元结构见图1,主要由制动夹钳和制动缸2部分组成。制动夹钳通过前后吊挂点悬挂安装在转向架构架上。其中,后吊挂点采用硫化橡胶吊轴作为弹性悬挂,具有一定的减振和吸能效果[5]。
在缓解状态下,制动夹钳单元自身存在一定的刚体运动自由度,为强非线性系统;而在制动状态下,刚体自由度为零,可近似视为线性结构。由于制动夹钳单元制动状态下的振动载荷远大于缓解状态[3],因此以制动状态下的制动夹钳单元为分析对象。

图1 制动夹钳单元结构
1.2 振动分析模型
求解动力学方程的方法一般包括逐步积分法和振型叠加法。逐步积分法是一种非线性求解方法,为获得较高的计算精度需耗用较多计算资源与时间;振型叠加法作为一种线性计算方法,对于线性度较高的系统,具有良好的计算精度和经济性。
制动状态下的制动夹钳单元具有较高的结构线性度,利用Abaqus软件对制动夹钳单元进行线性化建模,主要进行以下方面特殊处理:
(1)对存在转动连接的部位采用连接器替代绑定,既保证了模型线性度,同时不会对零部件自由度产生过度约束。
(2)通过试验验证,在振动状态下制动缸轴向两端的响应基本一致,说明制动缸在充气制动状态下,具有较好的轴向刚度,因此,可将制动缸等效为2个质量点分别耦合在双侧杠杆末端,并通过1个预压缩弹簧模拟轴向刚度(刚度值为60 kN/mm)。
(3)根据后吊挂点橡胶吊轴刚度的测试,在正常工作载荷下,橡胶刚度曲线保持较高线性度,为直接研究吊轴橡胶的各项刚度对制动夹钳单元频率响应特性的影响情况,采用套管模拟橡胶的各向刚度,各项刚度值为:轴向刚度500 N/mm;径向刚度5 000 N/mm;扭转刚度5 000 N·m/°;偏转刚度25 000 N·m/°。制动夹钳主要零件材料参数见表1。
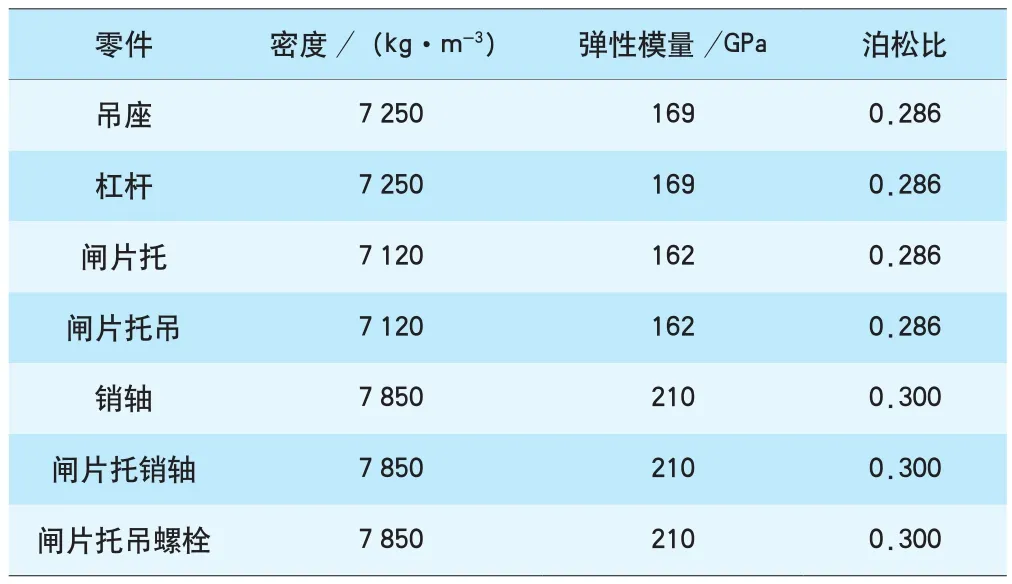
表1 制动夹钳主要零件材料参数
1.3 正弦扫频试验

图2 制动夹钳正弦扫频试验
为验证上述振动分析模型的合理性,在振动试验台上对制动夹钳单元进行横向和垂向正弦扫频试验(见图2)。其中,输入扫频振动量级为0.2g,扫频范围为5~320 Hz。在制动夹钳上选择3个具有代表性的测试响应点(见图3):杠杆中段销轴孔附近(1#测点)、杠杆后段制动缸安装孔附近(2#测点)和吊架底部中心(3#测点)。

图3 测点传感器布置
各测点频率响应曲线的试验结果与仿真分析结果对比见图4、图5。可以看出,仿真结果与试验结果在低频范围内基本保持相同趋势,在1阶和2阶响应峰值处,虽在响应频率和响应幅值上存在一定偏差(频率偏差最大约10 Hz),但仍较清晰地反映出制动夹钳结构的频率响应特性,说明前述振动分析模型具有较好的合理性。
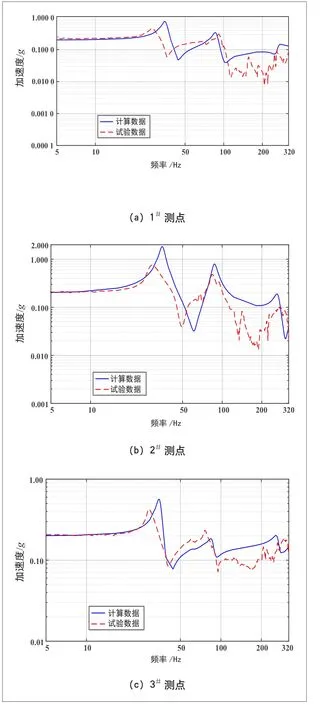
图4 横向扫频频率响应曲线
2 制动夹钳模态分析
针对振动分析模型,利用Abaqus软件进行模态分析,计算结果见表2、图6。制动夹钳在100 Hz以内的低阶模态共有5阶,其中,第1和第3阶模态振型表现为橡胶吊轴的径向变形及制动夹钳后部整体垂向摆动;第2和第5阶模态振型表现为橡胶吊轴的轴向变形及制动夹钳整体水平摆动;第4阶模态振型表现为双侧杠杆的垂向交错摆动。由此可以看出,除第4阶模态外,其余的第1、2、3、5阶模态均与制动夹钳的悬吊刚度(即橡胶吊轴刚度)有关,而一般构架上的激振频率主要集中在几十赫兹的低频段,说明制动夹钳的悬吊刚度对其振动特性的影响较大。

图5 垂向扫频频率响应曲线

表2 制动夹钳低阶模态频率 Hz

图6 制动夹钳低阶模态振型
结合图4、图5的结果可以看出,在垂向激振时,制动夹钳的1阶共振频率出现在第1阶模态频率附近,2阶共振频率出现在第3阶模态频率附近;在横向激振时,制动夹钳的1阶共振频率出现在第2阶模态频率附近,2阶共振频率出现在第5阶模态频率附近。这进一步反映了悬吊刚度对制动夹钳自身的振动响应存在重要影响。
3 悬吊刚度对频率响应的影响
利用上述模型,以测点1位置横向和垂向振动频率响应为目标,分别研究各向悬吊刚度对频率响应的影响。
3.1 轴向刚度影响分析
计算悬吊轴向刚度分别为500、1 000、2 000 N/mm(其他相关刚度参数见表3)时测点1位置的横向和垂向频率响应(见图7)。

表3 轴向刚度分析算例各向刚度参数
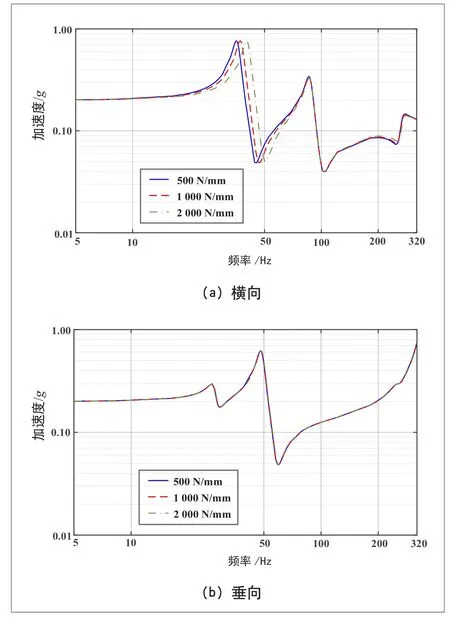
图7 轴向刚度对1#测点频率响应的影响
从图7(a)可以看出,随着悬吊轴向刚度值的增大,横向频率响应的1阶共振频率有所提高,但对1阶共振响应幅值和2阶共振影响不大;从图7(b)可以看出,3条曲线基本重合,说明悬吊轴向刚度对测点1位置的垂向频率响应特性基本无影响。
3.2 径向刚度影响分析
计算悬吊径向刚度分别为5 000、10 000、20 000 N/mm(其他相关刚度参数见表4)时测点1位置的横向和垂向频率响应(见图8)。
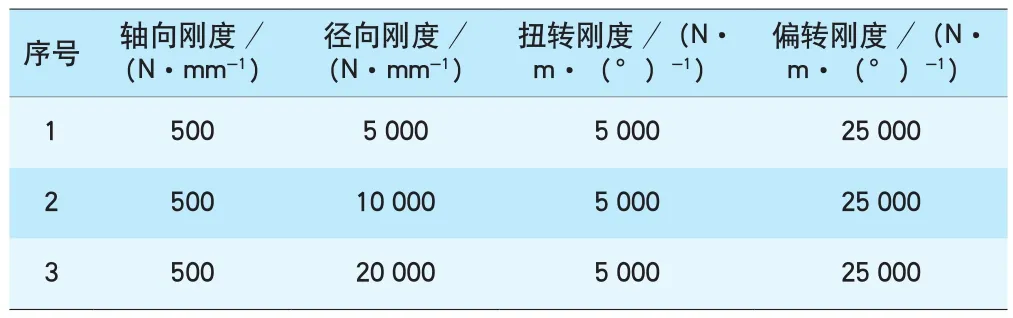
表4 径向刚度分析算例各向刚度参数

图8 径向刚度对1#测点频率响应的影响
从图8(a)可以看出,随着悬吊径向刚度值的增大,横向频率响应的1阶共振频率有较明显的提高,2阶共振频率也有所提高,响应幅值也发生相应改变;从图8(b)可以看出,随着悬吊径向刚度值的增大,垂向频率响应的1阶和2阶共振频率均有较明显的提高,响应幅值也发生相应改变,说明悬吊径向刚度对测点1位置的垂向频率响应特性的影响大于横向。
3.3 扭转和偏转刚度影响分析
计算悬吊扭转刚度分别为5 000、10 000、20 000 N·m/°,以及偏转刚度分别为25 000、50 000、200 000 N·m/°(其他相关刚度参数分别见表5、表6)时测点1位置的横向和垂向频率响应(见图9、图10)。
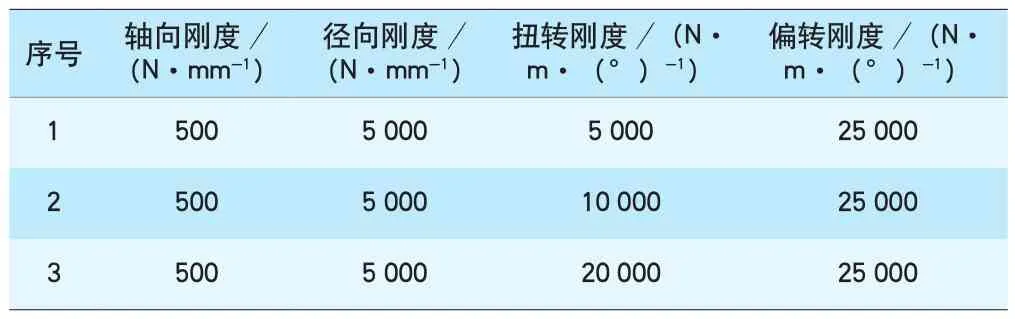
表5 扭转刚度分析算例各向刚度参数
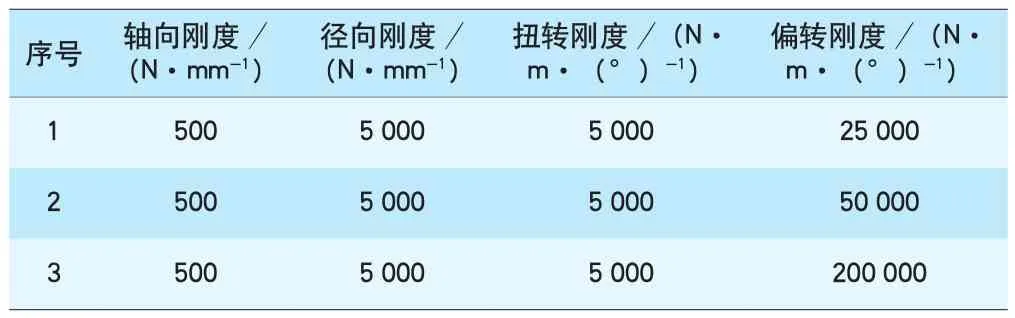
表6 偏转刚度分析算例各向刚度参数
从图9、图10可以看出,悬吊扭转刚度和偏转刚度对测点1位置的横向与垂向频率响应特性基本无影响。
各项悬吊刚度对测点2和测点3位置频率响应特性的影响情况与测点1位置具有相同特点,不再累述。
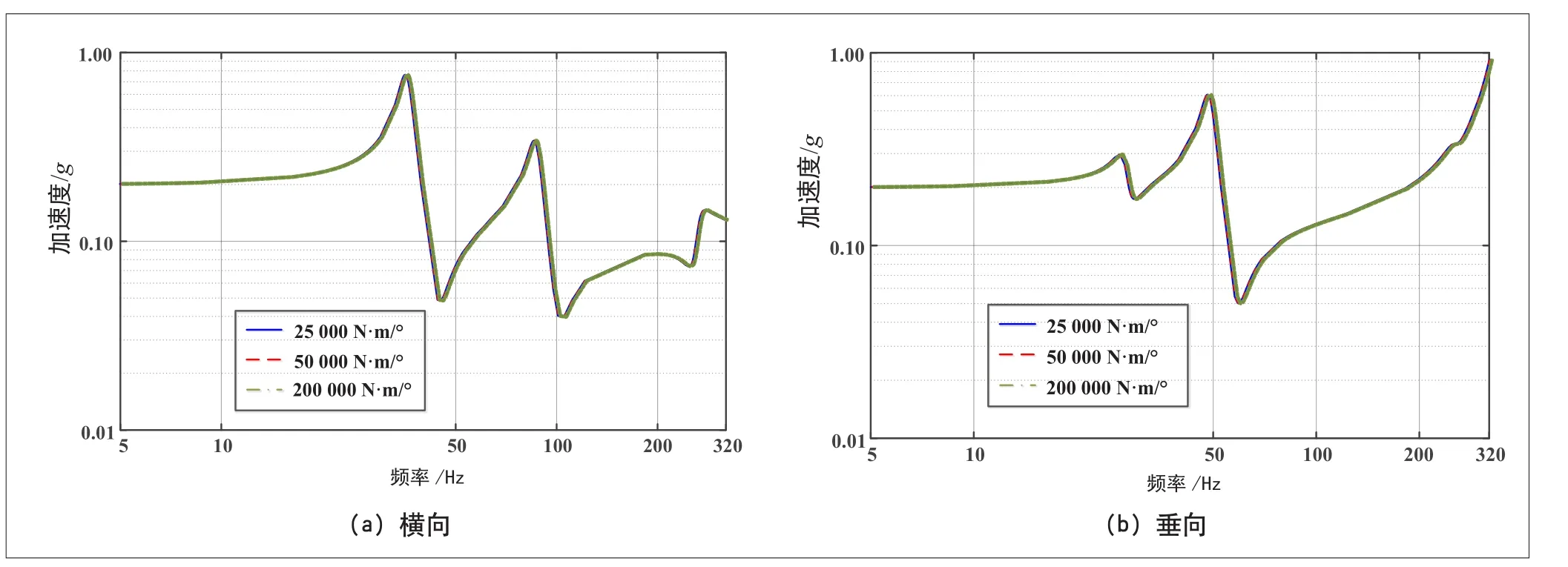
图9 扭转刚度对1#测点频率响应的影响
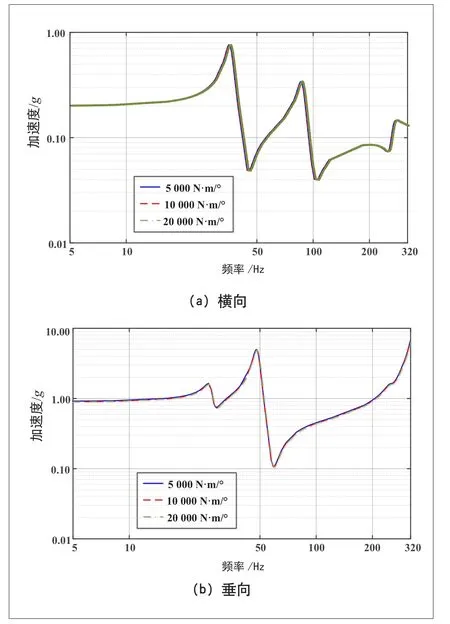
图10 偏转刚度对1#测点频率响应的影响
4 结论
(1)基于模态分析与振型叠加,建立制动夹钳线性振动分析模型,经正弦扫频试验对不同位置横向、垂向频率响应特性的对比,该模型能够较好反映出制动夹钳的低阶共振特征,证明该振动分析模型的合理性。
(2)制动夹钳单元的低阶(100 Hz以内)模态中,大多与悬吊刚度有关,且横向、垂向激振下的1阶、2阶共振频率都与相应的低阶模态频率接近,说明制动夹钳的悬吊刚度对其低频振动特性有重要影响。
(3)悬吊轴向刚度对制动夹钳横向激振下的1阶共振频率有一定影响,但对横向2阶共振与垂向振动响应特性基本无影响;悬吊径向刚度对制动夹钳的横向、垂向振动响应特性均有较明显的影响;悬吊扭转刚度和偏转刚度则对制动夹钳的横向、垂向振动响应特性基本无影响。
