制动力作用下CRTSⅡ型板式无砟轨道层间剪切破坏规律研究
2019-03-22李杨陈进杰王建西陈龙
李杨 ,陈进杰,3,王建西 ,陈龙
(1. 石家庄铁道大学 交通运输学院,河北 石家庄 050043;2. 石家庄铁道大学 土木工程学院,河北 石家庄 050043;3. 河北省交通安全与控制重点实验室,河北 石家庄 050043)
0 引言
CRTSⅡ型板式无砟轨道在我国得到了广泛应用,其结构特点是通过水泥乳化沥青砂浆调整层(简称CA砂浆层)将预制轨道板铺设在混凝土支承层或底座板上,并通过纵向钢筋对轨道板进行纵向连接[1]。CA砂浆层作用是在施工阶段对轨道结构进行充填调整,在运营过程中传递竖向、纵向和横向力,这就要求轨道板与CA砂浆层之间保证良好的黏结。然而,在线路运营过程中,轨道板与CA砂浆层之间的离缝伤损却比较常见[2]。
温度荷载是CRTSⅡ型板式无砟轨道发生离缝伤损的一个重要原因。由于材料热变形性能不同,加上轨道结构间存在不均匀温度差,轨道板与CA砂浆在温度作用下的变形难以协调,此时便容易发生离缝伤损。对于温度荷载作用下的层间传力与破坏机理,学者们做了相关研究[3-8]。除了温度荷载,列车荷载也是层间破坏的一个重要原因。列车制动,无砟轨道结构受到竖向力作用的同时,还受到纵向力作用,此时轨道板与CA砂浆层间将受到较大的剪切应力作用,这对层间的黏结会产生不利影响。但目前关于列车制动力的研究多集中于制动力在各层结构内的分布规律,缺乏对层间传力规律的研究,且模型都较为粗略,多将CA砂浆简化为线性弹簧,忽略了轨道板与CA砂浆黏结关系的非线性与伤损变化,缺乏对列车制动力作用下无砟轨道层间传力及伤损之间关系的研究,且一般将列车制动力按均布力考虑,与列车制动时的真实情况存在一定差异[9-13]。
针对上述问题,建立CRTSⅡ型板式无砟轨道结构三维精细化模型,根据轴距和车辆定距确定轮载与制动力加载位置,采用双线性内聚力模型表征轨道板与CA砂浆界面间的黏结特性,针对列车制动力对CRTSⅡ型板式无砟轨道剪切破坏的影响机理进行研究。
1 建立有限元模型
根据CRTSⅡ型板式无砟轨道结构实际形状尺寸,采用ABAQUS软件建立三维有限元实体模型(见图1),轨道板长6.45 m,板缝宽0.05 m,板厚0.20 m,CA砂浆层厚0.03 m,支承层厚0.30 m。为了消除边界效应的影响,取5块轨道板长度,取中间板作为主要研究对象。钢轨、轨道板、宽窄接缝、CA砂浆层及支承层采用缩减积分单元建模。宽窄接缝与相邻轨道板和CA砂浆层界面进行绑定约束。钢轨与轨道板间的扣件采用弹簧单元进行模拟,每个扣件使用一个弹簧单元进行模拟。弹簧单元的垂向刚度为35 kN/mm;横向刚度为50 kN/mm;纵向采用力与位移的双折线关系模拟扣件纵向阻力,位移<2 mm时,扣件纵向阻力随位移线性增加,位移>2 mm时扣件纵向阻力保持不变,扣件最大纵向阻力取9 kN/组。研究表明,CA砂浆的界面破坏主要发生在上表面,即CA砂浆与轨道板间界面,而CA砂浆与支承层黏结一般较好[14],因此模型中对CA砂浆层与支承层间进行绑定约束,在轨道板与CA砂浆层间建立界面单元,采用内聚力模型模拟界面单元本构关系。对模型两端的轨道板、CA砂浆层及支承层的端面施加纵向对称约束。对支承层下表面进行全约束。整个模型共划分为697 834个实体单元、32 895个界面单元。轨道板、CA砂浆层、宽窄接缝及支承层的材料参数见表1。

图1 CRTSⅡ型板式无砟轨道有限元模型
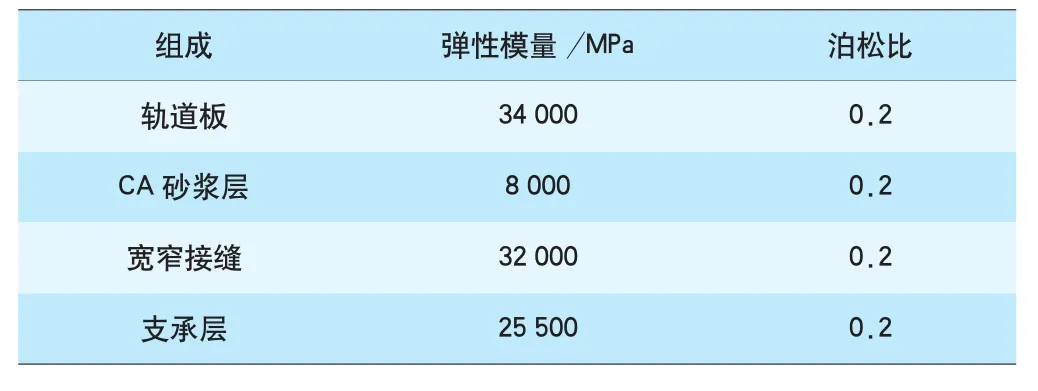
表1 模型材料参数
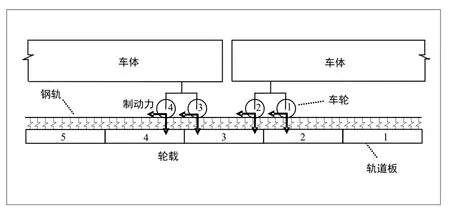
图2 车轮作用位置示意图
根据轴距和车辆定距确定轮载与制动力加载位置,两车体相邻的前后转向架车轮位于中间三块板上,加载位置、轨道板编号、车轮编号见图2。轮载与制动力分别通过在车轮与钢轨接触位置施加垂向集中力与纵向水平集中力的方式加载于钢轨上。参考CRH3型动车组车辆结构参数,转向架轴距取2.5 m,列车轴重取15 t。
2 界面应力-位移关系
轨道板与CA砂浆材料性能不同,其界面的黏结力与相对位移表现为一种非线性关系,即当相对位移较小时,黏结力随相对位移增大而增大;当界面应力达到界面黏结强度后,黏结力随相对位移的增大而减小,直至变为0。对于黏结力与相对位移的这种关系,双线性模型简单实用,能有效描述层间应力与相对位移的关系[14],因此,采用双线性模型对轨道板与CA砂浆的层间作用进行模拟。
层间黏结力本构模型见图3。相对位移较小时,黏结力随相对位移增大而增大,界面黏结强度为τf,此时对应的起始伤损位移为δ1;此后界面进入破坏阶段,黏结力随相对位移的增大而减小,当黏结力降到0时,对应的相对位移为δf,此时界面完全破坏。试验研究表明,CA砂浆与轨道板的法向拉伸黏结强度大于切向剪切强度[15]。在轮载作用下,轨道板与CA砂浆界面法向大部分受压,此时不会发生法向拉伸破坏,破坏模式主要为剪切破坏。但界面受压刚度及法向压缩强度尚无试验数据,且为了防止仿真分析中轨道板侵入CA砂浆,法向受压刚度及法向压缩强度需取较大数值,文献[14]将法向刚度及法向压缩强度设置为切向刚度及切向强度的100倍。
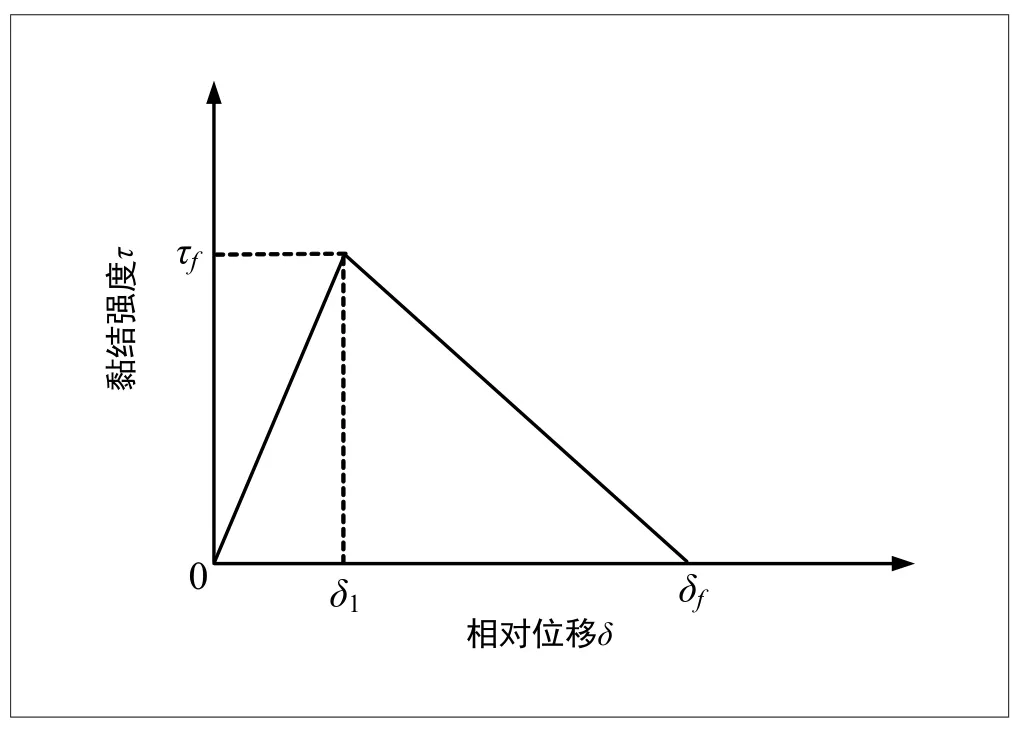
图3 层间黏结力本构模型
界面黏聚力-相对位移控制方程为:
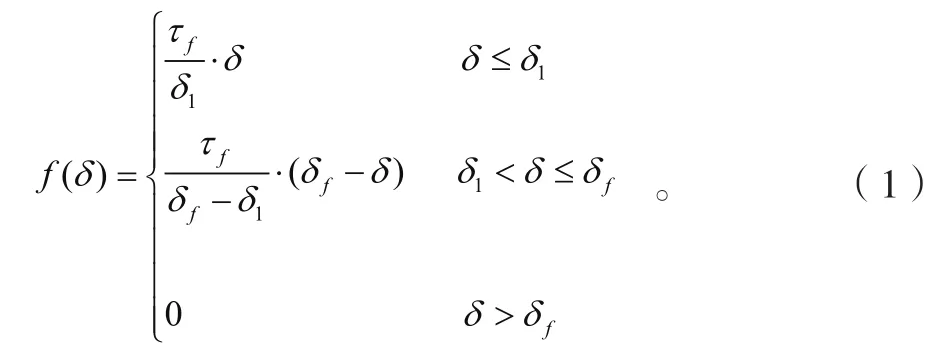
采用伤损参数D对界面伤损程度进行描述,定义为:

式中:为伤损值D达到1时的节点有效位移;为荷载历程中节点最大有效位移;为破坏起始时单元节点的有效位移;0<D<1时表示界面单元处于软化区域,D=1时表示界面单元破坏。
单元初始伤损判据采用二次应力准则,伤损演化采用能量法则:

式中:τn、τs、τt分别为正应力和 2个剪切应力;、、分别为正应力、第一剪切应力、第二剪切应力的黏结强度;〈〉表示压应力对结构的初始破坏不作贡献。
3 制动力率对层间伤损的影响
列车制动时,轨道结构将受到制动力的作用,制动力的大小可用制动力率来体现。制动力率定义为:

式中:θ为制动力率;T为制动力;P为列车竖向荷载。
各国规范对于θ的规定差异较大,其值介于0.150~0.350,最小有效制动力率甚至取为0.100。为了分析制动力率对无砟轨道层间传力与伤损的影响,θ分别取值0.100、0.225和0.350,对无砟轨道层间传力与伤损进行分析。为了考虑不同界面内聚力模型参数对结果的影响,取2种内聚力模型参数,极限剪切强度τf分别取 0.025 MPa和 0.075 MPa;δ1取值相同,取0.01 mm;δf取值相同,取2 mm[5]。2种内聚力模型本构关系见图4。
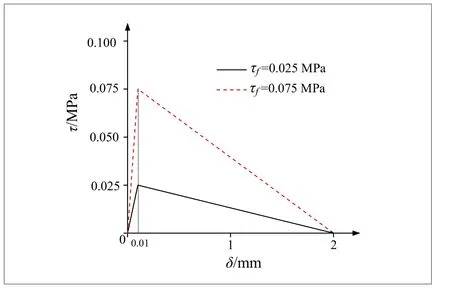
图4 2种内聚力模型本构关系
当τf=0.075 MPa、θ=0.350时,轨道板2、轨道板3、轨道板4范围内,沿钢轨正下方的轨道板与CA砂浆层间纵向剪切应力见图5。可见,同一转向架2个车轮下的纵向剪切应力有相互叠加的部分,但前后车体的纵向剪切应力基本互不影响,且4个车轮下的纵向剪切应力分布规律基本一致,因此选取其中1个车轮下的剪切应力分布规律进行研究。

图5 剪切应力沿纵向整体分布规律
为了便于分析,取3号车轮对应钢轨正下方的轨道板与CA砂浆层间路径为纵向路径,纵向路径长度取半块板的长度;取车轮作用位置下与纵向路径垂直的路径为横向路径。2条路径位置示意见图6。车轮位于扣件2和扣件5上方,制动力方向从扣件3指向扣件1。
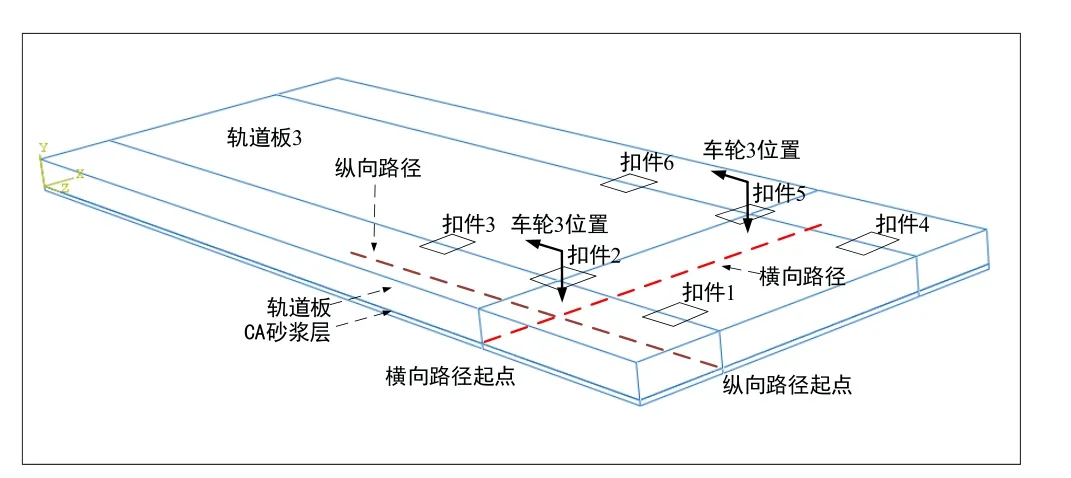
图6 横纵路径示意图
CRH3型动车组列车轴重取15 t,针对不利工况,考虑列车运行振动、冲击荷载的影响及一定的安全储量,动轮载取静轮载的3倍,单个车轮的垂向动轮载取为225 kN。θ分别取0.100、0.225和0.350,对应制动力分别为22.500、50.625、78.750 kN。当τf=0.075 MPa、θ=0.350时,纵向路径上的横向剪切应力与纵向剪切应力见图7(a)。可见,纵向路径上,横向剪切应力远小于纵向剪切应力,因此对于纵向路径,将只取纵向剪切应力进行研究。不同制动力率下纵向路径上的纵向剪切应力与伤损值分别见图7(b)和图7(c)。由图7(b)可见,扣件位置处正下方纵向剪切应力接近于0,在扣件两侧会出现正负2个方向的纵向剪切应力峰值,与图7(c)相对应,扣件正下方的伤损值较小,而扣件两侧15~20 cm则出现了伤损值峰值。由图7(c)可见,当τf=0.025 MPa时,纵向路径上并不会出现伤损。当τf=0.075 MPa时,纵向路径上的界面伤损峰值介于0~1,说明在此内聚力模型参数下,界面会发生伤损,而不会发生破坏。在某些频繁制动区段,剪切应力的加载—卸载历程将在界面间反复循环,界面间有出现疲劳剪切破坏的可能,因此在频繁制动区段需注意层间离缝的防治。同时,对于相同的内聚力模型参数,不同制动力率下在纵向路径上的界面伤损值和界面剪切应力的分布差异很小,说明制动力率对纵向路径上的剪切应力和界面伤损值分布影响很小,但内聚力模型参数对纵向路径上的剪切应力和界面伤损值分布影响较大。

图7 制动力率对纵向路径上的剪切应力与伤损值的影响
θ分别取值 0.100、0.225和 0.350。当τf=0.075 MPa、θ=0.350时,横向路径上的横向剪切应力与纵向剪切应力见图8(a)。可见,横向路径上,横向剪切应力远大于纵向剪切应力,因此对横向路径将只取横向剪切应力进行研究。不同制动力率下横向路径上的横向剪切应力与伤损值分别见图8(b)和图8(c)。由图8(b)可见,扣件位置处扣件正下方的纵向剪切应力接近于0,在扣件两侧会出现正负2个方向的横向剪切应力峰值,与图8(c)相对应,扣件正下方的伤损值较小,而扣件两侧则出现了伤损值峰值。由图8(c)可见,横向路径上的界面伤损峰值介于0~1,说明在此内聚力模型参数下,界面会发生伤损,但不会发生破坏。从横向路径上看,扣件两侧15~20 cm伤损值最大,而轨道板中间区域的伤损值为0,可见制动力对于扣件附近的层间黏结破坏较大。同时,对于同一内聚力模型,不同制动力率在横向路径上的界面伤损值和界面剪切应力的分布差异很小,说明制动力率对横向路径上的界面伤损和剪切应力分布影响很小。
综合纵向路径与横向路径上的结果可知,制动力率对于界面伤损值分布与界面剪切应力分布影响较小,但界面的黏结性能对于制动力作用下的层间伤损影响较大。
4 内聚力模型参数对层间伤损的影响
轨道板与CA砂浆层的黏结状态受到材料状态、施工质量等多种因素影响,导致层间内聚力模型参数的随机性较大[15],并由上述分析可知,界面黏结性能对于制动力作用下的层间伤损影响较大,因此研究内聚力模型参数对于制动力作用下层间传力和伤损的影响具有必要性。选取τf和δ1两个参数进行双变量分析。τf分别为0.025、0.075、0.125 MPa,δ1分别取0.01、0.05、0.10 mm,共设置9组(3×3)内聚力模型参数(见图9)。可见,当τf取某一定值时,δ1越大,内聚力单元刚度越小;当δ1取某一定值时,τf越大,内聚力单元刚度越大。其他参数的取值为:单个车轮的垂向动轮载取225 kN,θ取 0.35,δf取 2 mm。
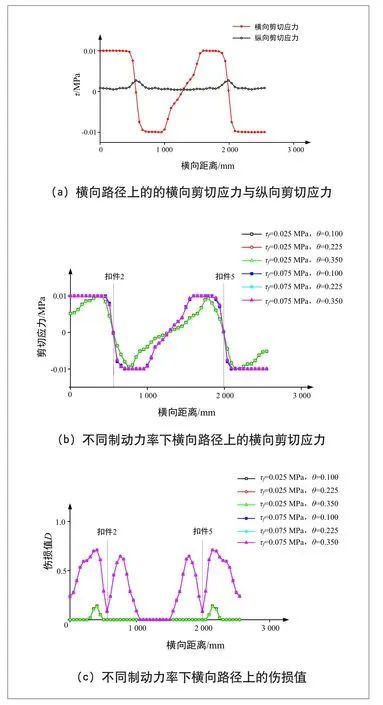
图8 制动力率对横向路径上的剪切应力与伤损值的影响

图9 不同破坏起始位移下的内聚力模型本构关系
对于内聚力模型参数,制动力作用下纵向路径上的界面纵向剪切应力与界面伤损值见图10。由图10(a)可见,对于同一δ1,τf越大,纵向剪切应力越大;对于同一τf,δ1越大,纵向剪切应力越小;当δ1=0.01 mm,τf=0.075、0.125 MPa时,纵向路径上的纵向剪切应力明显大于其他内聚力参数下的纵向剪切应力。由图10(b)可见,仅当δ1=0.01 mm、τf=0.075 MPa或0.125 MPa时,纵向路径上出现伤损,其他内聚力模型参数下纵向路径并未出现伤损,而上述2种内聚力参数对应的界面刚度均大于其他7组内聚力模型参数。

图10 内聚力模型参数对纵向路径上的伤损值与剪切应力的影响
不同内聚力下,制动力作用下横向路径上的界面横向剪切应力与界面伤损值见图11。由图11(a)可见,对于不同内聚力模型参数,横向路径上的横向剪切应力分布规律与纵向路径上的纵向剪切应力分布规律具有一致性,δ1=0.01 mm时,横向路径上的横向剪切应力大于其他内聚力参数下的横向剪切应力。由图11(b)可见,当δ1=0.01 mm,对于3个τf值,横向路径上均出现伤损,且τf越大,内聚力单元刚度越大,伤损值越大,可见过大的剪切刚度会对层间界面的黏结产生不利影响。当δ1=0.05、0.10 mm时,横向路径上并未出现伤损。
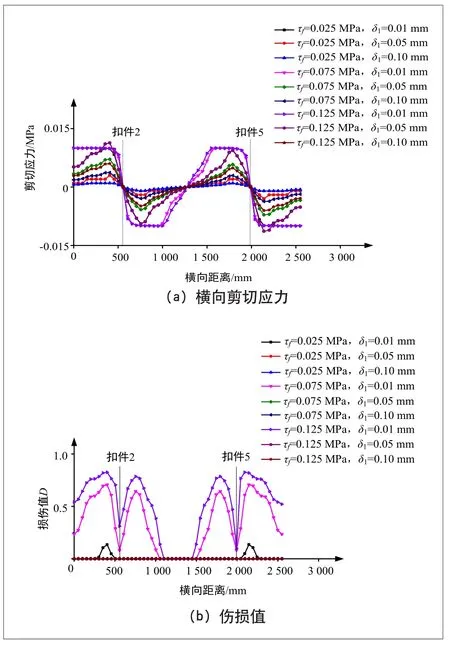
图11 内聚力模型参数对横向路径上的伤损值与剪切应力的影响
综合横纵2条路径来看,相同制动力作用下,起始伤损位移值δ1越小,界面越容易发生伤损;对于同一起始伤损位移值δ1,剪切强度τf越大,界面刚度越大,单元伤损程度越高。
5 结论
(1)制动力率对于界面剪切应力分布与伤损分布影响较小,界面的黏结性能对于制动力作用下界面剪切应力与伤损分布影响较大。
(2)制动力对扣件四周的轨道板与CA砂浆界面黏结破坏作用较大,对于板中间位置界面黏结基本无影响。
(3)相同制动力作用下,界面起始伤损位移δ1越小,界面越容易发生伤损。
(4)过大的剪切刚度会对层间界面的黏结产生不利影响。
