智能玩具赛车赛道图像的畸变校正问题研究

李丹美,王 凯

(东华大学 信息科学与技术学院，上海 201620)

0 引言

随着近年来智能科技的飞速发展，多数领域也开始涉及到智能技术。玩具行业便是其中之一。近年来，玩具行业开始逐渐生产一种大型的有轨玩具车投放到大型的商场、游乐场中供孩子们娱乐。目前，玩具行业生产的带有赛道的玩具赛车主要还是基于轨道的，通过跑道上面的轨道来控制玩具车的行驶。更智能化的玩具赛车是基于赛道的。这种玩具赛车主要通过摄像头获取道路图像信息，然后通过对道路图像的处理来提供控制赛车行驶的数据。

由于玩具赛车上面摄像头固定的位置所限，所采集到的图像存在梯形失真，不能直接被用来做控制数据，所以需要对采集到的图像进行处理，得到相对来说更准确的赛道数据信息，然后再传给智能玩具赛车的控制模块，保证能够准确地控制玩具赛车的行驶。

本文的研究主要是对智能玩具赛车采集到的赛道畸变图像做校正处理。由于采用的是二值摄像头，所以直接从二值图像开始进行处理，通过对图像进行边缘检测以及轮廓提取来确定校正取点，以此来校正失真图像。最后通过对校正过程的改进使得校正算法更适合本次图像的梯形校正，以达到更好的处理效果。

1 几何畸变

1.1 畸变类型

图像的畸变主要是指在生成可视图像时由于各种原因导致图像成像时扭曲变形、旋转、伸展等各种失真，与原图像相比位置、形状等畸变。主要的畸变类型有：桶形失真、枕形失真、梯形失真、鱼眼失真等[1]，各种失真模型如图1所示，虚线构成的方块为原不失真图像，实线构成的多边形为畸变后的图像。

图1 几种图像畸变几何模型

根据采集到的十字道路的图像可以判断出，本次研究的课题中，摄像头采集到的图像主要产生畸变类型属于梯形畸变。

1.2 梯形畸变的产生和影响

摄像头安装的位置近似于机器人的最高点，由于摄像头要采集机器人前面的即将驶入的道路信息，所以摄像头安装后摄像镜头为向前下方倾斜的情况(如图2所示)，此时拍摄效果类似于人眼获取前面道路信息的效果，会呈现出近宽远窄的情况，因此获取的图像信息会产生梯形畸变，使得本为同等宽度的赛道，最后采集到的效果为近宽远窄的情况。图3所示分别为十字入口、弯道入口时采集到的赛道图像。

图2 摄像头采集图像时的高度和距离模型

图3 摄像头拍摄到的失真图像

由于采集到的图像发生了畸变，因此对图像的视觉感受便是赛道发生了扭曲，这样提取的中心线与实际情况下的中心线会发生不同程度的偏差，非常不利于玩具赛车的行驶。因此，这种产生畸变的图像，一方面会使得判断直道、弯道、环道时容易出现失误，另一方面通过中心线进行行驶控制时会对速度和方向产生较大的干扰。所以，对机器人采集到的畸变图像进行图像校正处理是一个急需解决的问题。

2 梯形失真校正

对于图像的失真校正，就是将畸变的图像还原出垂直看向赛道的情况。校正过程主要分为预处理和畸变校正两部分。处理框图如图4所示。

图4 图像矫正流程图

2.1 图像预处理

在对图像进行畸变校正之前需要先对采集到的图像进行预处理操作。预处理的作用是优化采集到的图像，减少后期主要操作时无用信息带来的干扰，增加处理结果的准确性。预处理主要包括边缘检测、形态学运算、轮廓提取等几个步骤。边缘检测主要用来检测出赛道的边界线，然后通过形态学的膨胀腐蚀运算来优化边界线，减少边界线检测时的噪声影响，最后再通过轮廓提取来提取出赛道的边界线。

本次研究所用的边缘检测算子主要有Sobel算子和Prewitt算子[2-4]。这两种算子的3×3模板如图5所示。算法定义如下式：

(1)

其中，G为图像的梯度，gx和gy分别为该点水平方向和垂直方向上的图像灰度值。公式(2)和(3)分别为Sobel模板和Prewitt模板下的gx和gy，其中z项为灰度。

(2)

(3)

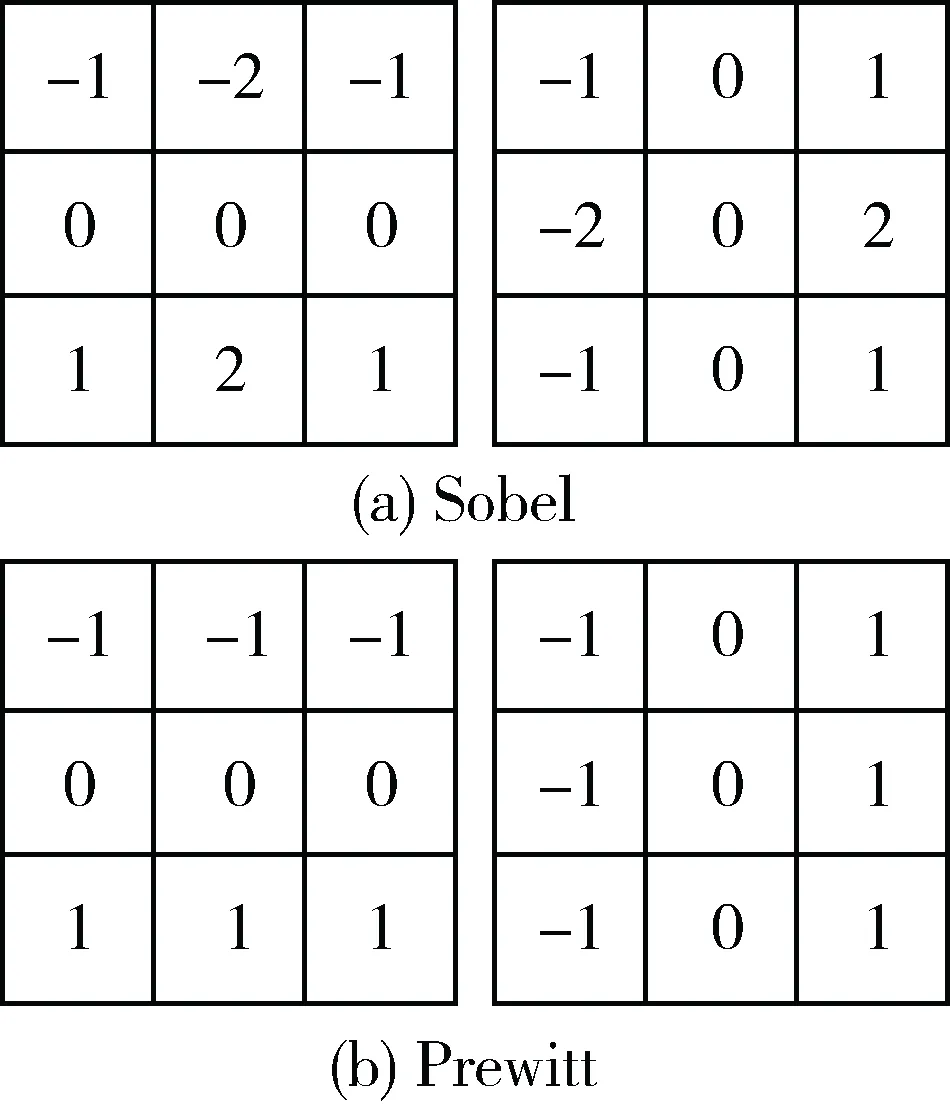
图5 边缘检测两种算子的3×3模板

本次研究的课题中轮廓提取所用的方法为Radon变换。Radon变换具有一定的抗干扰能力，同时也易于实现。Radon变换定义如下：

(4)

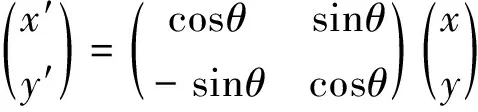
(5)

其中原函数f(x,y)为图像在(x,y)处的灰度。Radon变换就是将待处理的图像从二维坐标转换成ρ-θ空间，即为直线在ρ-θ空间的水平投影。从几何意义上可以理解为二维函数f(x,y)在θ方向上(沿x坐标轴逆时针成θ角)距离原点x′的长度在x轴的水平投影值[5]。通过检测Radon变换矩阵中的峰值便可以确定图像的边缘轮廓，轮廓图像如图6所示。

图6 两种不同的算子处理之后提取的轮廓图像

经分析对比，在边缘检测的时候由两种算子分别处理之后再提取的轮廓结果差别不大，但是仔细对比之后发现，针对本次图片使用sobel算子处理之后得出的效果相对更好一点。

2.2 畸变校正及改进

2.2.1畸变校正

畸变的存在不利于对图像的辨认、分析和判断。由于采集到的图像存在的畸变较大，特别是弯道和环道图像，若不进行校正处理将会对后面的处理带来较大的误差。因此为了提高图像处理后输出数据的准确性，在图像处理之前首先需要对图像进行校正处理，而校正的准确度也将会直接影响到处理之后数据的准确性。

(6)

(7)

校正结果如图7所示。

图7 校正后图像

2.2.2校正改进

由于校正出来的图像结果还存在有失真情况，特别是弯道的处理结果不太成功，经过多次仿真实验，归其原因为原图像为二值图像，灰度值非0即1，轮廓在原图像上不能正常显示，所以在进行取点时随机性过大，分别会造成不同程度的失真。

因此本次研究同时对以上方法进行了改进。在对图像取点时将不再对整合的原图像进行取点，而是直接针对提取的轮廓图像进行取点，然后进行轮廓图像的校正，之后再进行插值及填充补偿。

改进之后的算法基本步骤为：

(1)对采集到的图像进行边缘检测及轮廓提取；

(2)针对提取的轮廓图像进行图像校正及邻域插值，保证校正后的轮廓的连续性；

(3)对校正后的轮廓图像使用图像填充技术进行填充补偿，还原图像的连通性，保证道路信息的完整。这里使用的填充算法的基本思想为：满足待填充的边界约束条件(式(8))的闭合区域内的点可以构成一个可行域点集T，T内的点包含了图案上的点和待填充的点。基于约束条件，可以将填充区域转化为可行区域，而可行区域的填充则是一个定向搜索问题，这样在填充的同时也解决了效率问题[7]。

(8)

其中fi(x)=0是闭合图形的第i端曲线方程。

得到的校正后的赛道图像如图8所示。

图8 改进后的校正图像

3 实验结果分析

本次实验研究主要采用MATLAB编程处理。从上面的图像校正结果可以对比分析出改进方法的优点主要有：(1)由于只有轮廓的灰度为白色，所以取点时比较准确；(2)对于十字赛道的处理，在处理之后不仅校正了直道部分，通向两边的赛道在校正的同时也保证了不失真；(3)对于弯道的处理，通过准确取点，也有效地改善了校正的结果。通过良好的校正结果，对之后要研究的中心线提取、路径识别等问题也做了充分的准备。

本次研究中有待改进之处为：由于条件限制，采集赛道信息的设备不够齐全，所以采集到的赛道图像过于单一，校正方法具有一定的针对性。因此接下来要解决的便是针对更多种类的赛道图像进行研究，将本文中的方法升级到能够适应多种赛道情况，提高其有效性。