基于连续波多普勒雷达的手势信号识别算法
2019-03-22崔恒荣吴江林谢吉成
刘 钊,崔恒荣,吴江林,谢吉成,刘 涛
(东华大学 信息科学与技术学院,上海 201620)
0 引言
在过去几十年中,计算机技术飞速发展,计算机在各行各业为人类提供着服务,人类与计算机密不可分,人与计算机的信息交互不可或缺。手势是一种自然、直观的人机交互手段,以手势作为计算机的输入,已经成为一种趋势,手势识别在人机交互技术上的应用前景,极大地促进了手势识别的研究发展。
雷达向物体表面发射电磁波,一部分电磁波会携带可以解算出物体形状轮廓的多普勒频移信息反射回来,进而实现对动态物体的检测。
如图1所示,理论上雷达可通过对反射的波形中所携带的目标位置、速度、散射截面大小等信息的混频处理,得到动态手势的相关信息,再通过数字信号处理的方法进行后续分析[1]。
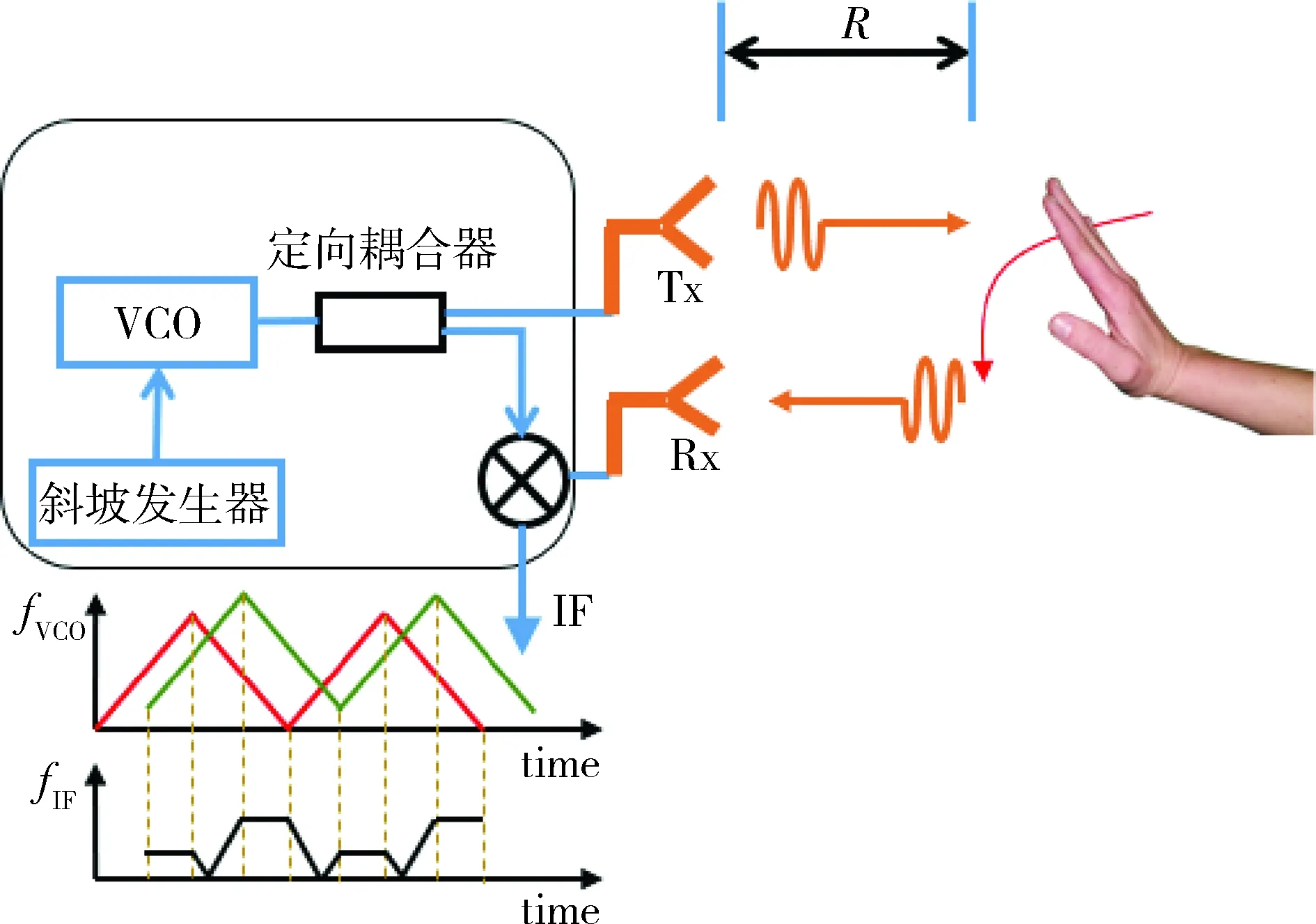
图1 雷达采集动态手势信号示意图
本文采集的手势信号为过程信号,当手势以速度v动态经过时,会产生多普勒信号,其频率fD为:
(1)
手势的运动过程是一个时间遍历信号,且速度、距离变化多样,单一的频域变换的方法难以识别多普勒雷达接收的手势信号。因而本文将先利用分段快速傅里叶变换(Fast Fourier Transform,FFT)对信号进行处理,提取频域信息,再结合机器学习算法对手势进行分类。
研究人员已开始使用雷达来进行动态物体的检测和识别,JAIME LIEN等人曾设计了soli雷达系统来捕获手势动作,其利用雷达波照射手部,接收多个来自动态散射中心叠加的反射信号,并将接收到的信号转换为抽象表示,再利用机器学习的技术实现了对手势的分类和识别[2]。机器学习不仅可以对数据进行快速处理,还可对问题进行预测、分类,其在包含手势分类在内的模式识别领域拥有极大的发展潜力。TAKAYOSHI YAMASHITA等人提出了“bottom-up structured”深度卷积神经网络实现了对6种静态手势的分类,其正确率达88.78%[3]。李富等人采用基于连续隐马尔科夫模型,实现了对不同用户手指滑动的原始手势特征的辨别,进而实现了身份验证,其错误率为1.22%[4]。张芷君等人提出协同重排序法的手势参数进行分解,利用k-最邻近算法实现各局部单元的估计姿态,结合全局姿态估计,可在30 ms内完成静态手势识别,其最大平均估计误差小于10。[5]。
相较于已有的研究成果,本文结合雷达检测、信号处理及机器学习,面向嵌入式平台,自行采集手势信号作为数据集,提出分段FFT提取手势的时-频域信息以作为一种新的算法输入信号,采用拓扑支持向量机(Support Vector Machine,SVM)算法结构,为动态手势识别提供新的方法和应用手段。
1 手势雷达硬件平台
本文利用ARM微控制单元STM32F405RGT6和多普勒雷达硬件平台实现对信号的采集及处理,继而传给上位机,进而提供了一个算法研发的硬件系统平台,硬件设备如图2所示。

图2 手势雷达硬件设备
现阶段对手势识别的研究往往以手势图像作为数据集,多数课题以静态手势数据库Thomas Moselund等作为数据集进行训练和测试[3]。而本文以手势雷达信号作为模型的输入,所以需要自行采集相关手势信息。
雷达装置采集的信息为时域信息,而受不同人手型、手速差异的影响,含时域、频域信息能更直观地表达手势信息,FFT是最经典的频域分析方法[6]。经采集实验发现,1 024个数据点可完整恰当地表达出一个实时手势信号。如直接对1 024点数据进行FFT不会降低数据的维度,而以32点数据为一组进行FFT处理,则会有较为良好的效果。
结合本文需求,参考常用的串口调试助手,数据采集系统图形用户界面(Graphical User Interfaces,GUI)如图3所示。
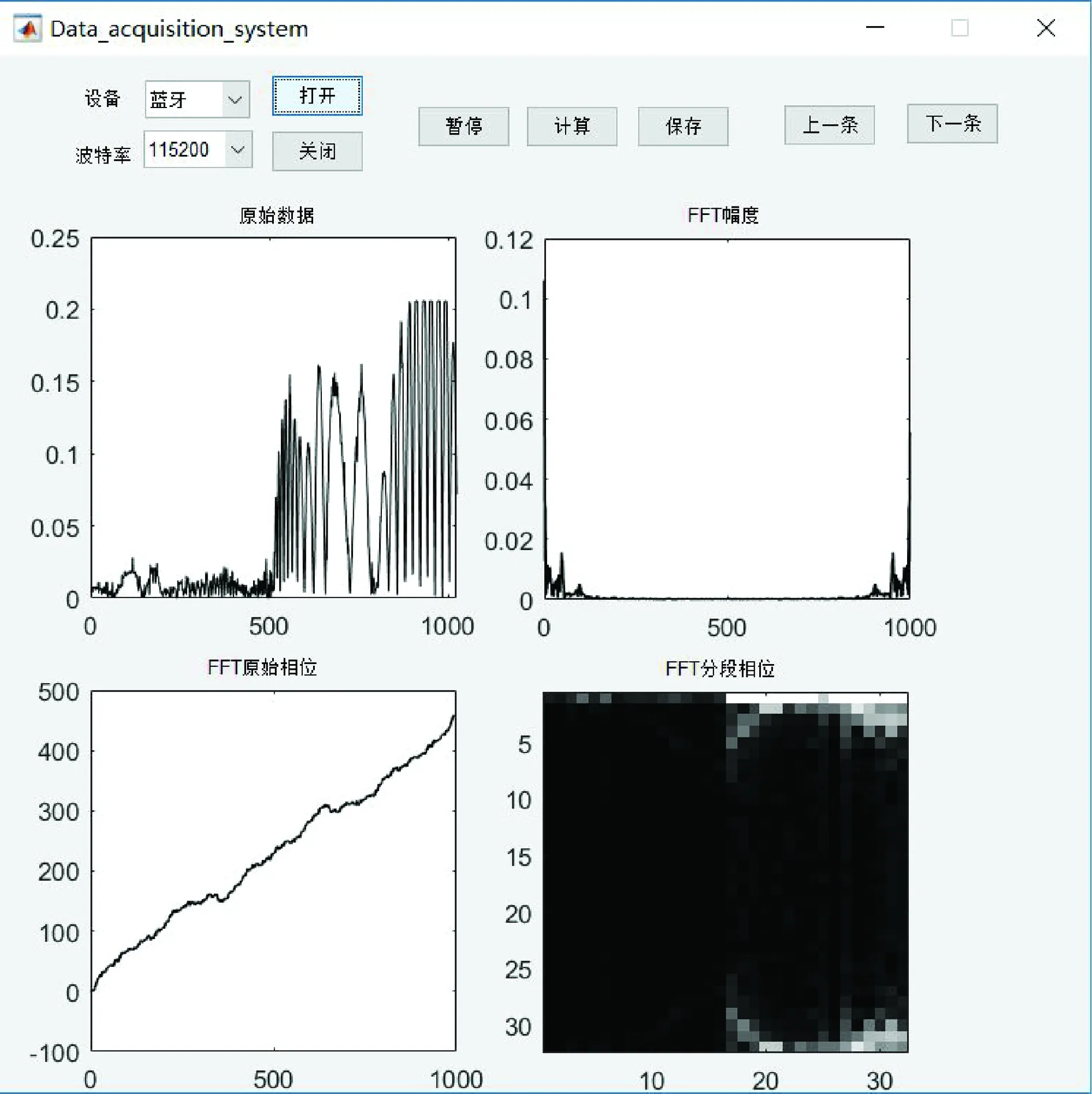
图3 GUI界面
2 基于SVM的手势分类模型
2.1 手势一维信号至二维图像转换
雷达手势信号预处理的主要目的就是将一维手势信号转换为同时包含时域和频域信息的二维信号。一维的手势信号是时域信号,无法直接表现出频率变化规律,傅里叶变换可以将时域信号变换为频域信号。经前期预采集实验,以每1 024个点为一组信号表征一个手势动作,每秒可采集512个数据点,采集过程历时2 s,采集信号经模数转换,表现为电压形式。本文尝试进行全段(信号长度N=1 024)FFT运算进行预处理,如图4(b)所示。可以看出,全段FFT没有降低数据维度,也没有保存时域信息,不利于后续数据处理。而经32点分段FFT得到的像素为32×32的二维图既保存了时域信号,也捕获了频域信息,如图4(c)所示,其像素颜色深浅代表了其电压大小,为之后的模型建立与求解创造了有利条件。

图4 不同信号长度FFT结果图
2.2 基于SVM的机器学习算法
目前,常用的手势识别算法有人工神经网络(Artificial Neural Network,ANN)及隐马尔科夫模型(Hidden Markov Model,HMM)两类。
ANN在静态手势的识别中应用较多,其自组织、自学习和抗噪声能力强,但神经网络易受到非线性以及维数灾难的干扰,容易产生局部极小点问题。神经网络在手势的识别中多为图像识别技术,常以手势图像作为输入,其建模需要一定的运算成本[7]。
HMM可以详细地分解手势信号的时空变化,相较于神经网络更适用于动态手势识别,但需人工提取手势特征,过程复杂且对陌生场景适应能力不强[8]。
SVM基于结构风险最小化原则以及统计学理论VC准则,可对本文有限的手势信号进行分类[9]。
SVM主要有线性和非线性两种方式,对于线性可分的数据,决策函数类似于线性拟合,该超平面f(x)可以表示为:
f(x)=ωTx+b
(2)
其中ω是权重向量,x为训练元组,b为偏移。不难看出,线性的SVM与线性规划问题相似,对本文较简洁的数据输入,SVM比ANN及HMM更简便,在CPU中即可快速完成运算。当有新的x进入分类器时,将根据其与决策边界的对应关系对其进行分类,相应的决策函数g(x)为:
g(x)=sign(ωTx+b)
(3)
而本文的数据经过了分段FFT运算,已从一维数据变换为32*32的数组,成为了一个高维的非线性分类问题,因而需要将手势信号的FFT运算结果映射到32维空间,在32维空间中构造线性最优分类面对手势信息进行分类,即可将低维空间非线性问题转化为32维空间线性可分问题。本文手势分类模型主要环节如图5所示。

图5 手势分类模型
一次支持向量机只可进行一次二分类,针对所研究的靠近、远离、挥手与握拳四种手势的分类问题,可采用拓扑结构通过3个SVM分类器来实现分类。经研究,远离和靠近与挥手和握拳之间的频谱有着较大的差异,应将其用第一个分类器分为两大类,然后再分别使用一个分类器,完成对手势的四分类,如图5(d)所示。为将低维空间非线性问题转化为32维空间线性可分问题,引入了核函数,而原来的线性分类函数g(x)被改造为:
(4)
其中,K(·)是核函数,yi∈{-1,+1}为手势信号xi实际分类,g(x)的值决定了手势信号x的隶属度。构造一个最优超平面即找到所有的非零值αi,作为任意手势向量xi最优超平面的支持向量系数,以达到SVM保留非常小数量的支持向量训练点的理想情况,提供一个紧凑的手势分类器。
选择不同的核函数,可以构造不同手势分类器。非线性支持向量机算法常用的核函数有如下四种,本文将利用尝试法寻找各SVM中最优核函数。
(1)线性核函数
K(x,xi)=xT·xi
(5)
(2)多项式核函数(多项式次数d≥1,d=1时退化为线性核)
(6)
(3)高斯核函数(高斯核带宽δ>0)
(7)
(4)sigmoid核函数(tanh为双曲正切函数,η>0,θ<0)
K(x,xi)=tanh(η〈xT,xi〉+θ)
(8)
3 实验设计与分析
3.1 手势信号数据库的建立
为使模型训练的效果具有普遍性,需利用数据采集系统采集具有一定样本容量的数据集。按照实际应用情况,本文邀请了多位师生,按照各自的习惯完成了有效的靠近、远离、挥手及握拳动作各1 000次。
本文对4 000条手势信号采集后完成了FFT处理等相关工作,作为本次实验的数据集。在4组1 000条手势信号中,各随机选取其中的900条对SVM模型进行训练,其余的100条作为测试集进行实验验证。
3.2 实验结果
SVM进行分类时,核函数的选取对结果有重要的影响,目前对于核函数选取没有统一的方法,经验法与尝试法是较常见的方法[10]。本文对三次SVM尝试了不同的核函数,其训练结果如表1所示。

表1 训练结果
由表1可得最佳的核函数组合方案为:SVM1选择线性核,SVM2选择多项式核,SVM3选择高斯核,训练集分类结果如图6所示。

图6 训练集分类结果
由图6可以看出,训练集分类正确率为90.69%(3 265/3 600)。 利用最佳方案,测试集分类结果如图7所示。
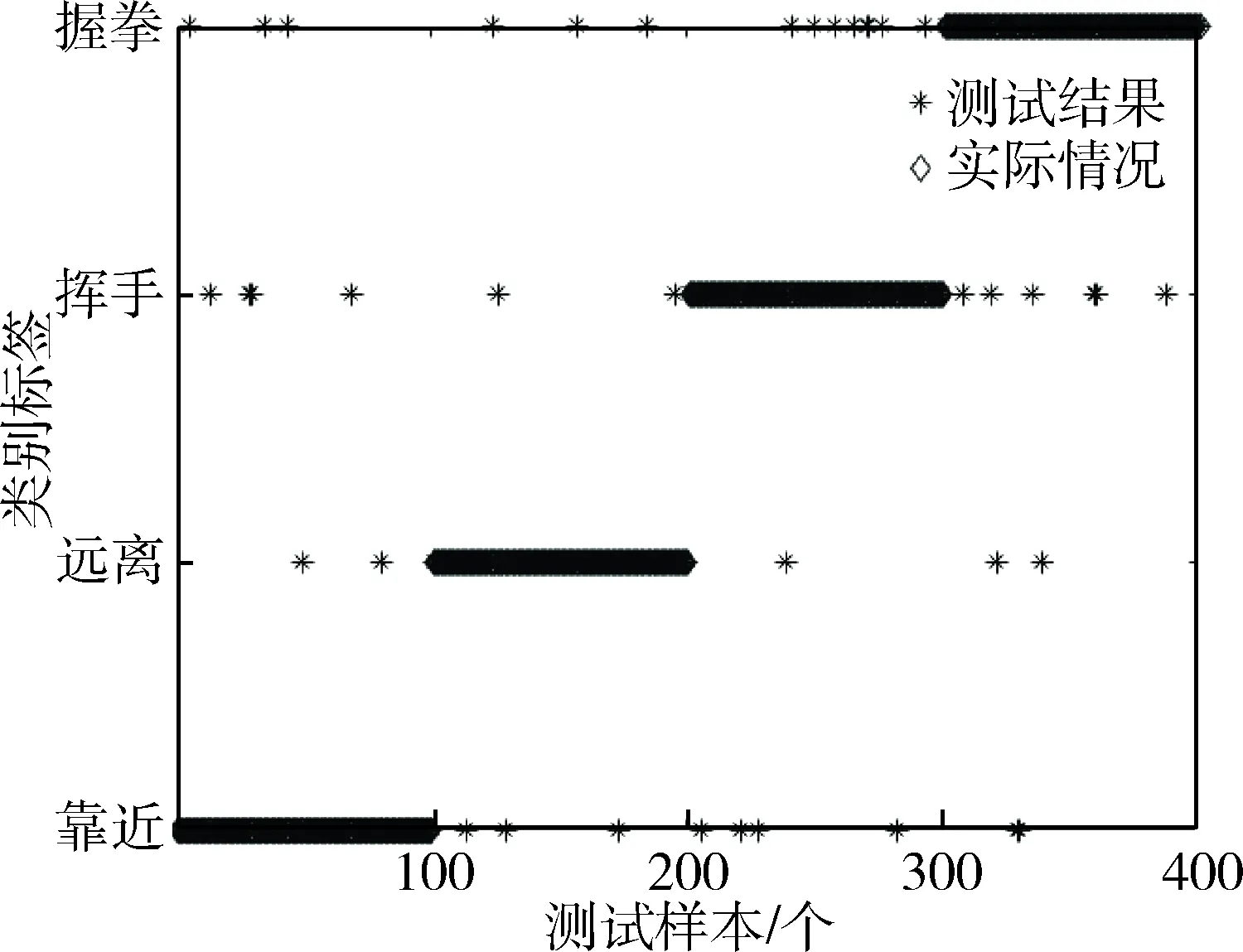
图7 测试集分类结果
由图7可以看出,测试集分类正确率为90.25%(361/400)。
4 结论
本文面向嵌入式系统,利用多普勒雷达传感器,接收动态手势信号,并用分段FFT对手势的时-频域信息进行整合,以作为拓扑SVM输入量,实现了对手势信号的分类和识别,该系统具有实时采集、快速分类的特点,为动态手势分类提供了新的方法。
