轴耦合道路模拟试验技术关键参数分析
2019-03-22李航周德泉李开标陈禹刘建文
李航,周德泉,李开标,陈禹,刘建文
轴耦合道路模拟试验技术关键参数分析
李航,周德泉,李开标,陈禹,刘建文
(广州汽车集团股份有限公司汽车工程研究院,广东 广州 511434)
基于6自由度轴耦合道路模拟试验系统,介绍了道路模拟试验的基本原理,通过伪损伤计算、频谱分析等对试验过程中设备系统、车辆系统的主要影响参数进行研究,结果表明不同控制信号、控制频段、车辆载荷、减振器温度对试验结果均有不同程度的影响。
道路模拟;迭代参数;控制信号
前言
道路模拟试验是验证汽车整车和零部件结构可靠性的重要手段,因具有试验周期短、重复性好、可长时间不间断试验等特点备受青睐。其技术核心是远程参数控制(Remote Parameter Control,简称RPC),此基础理论在上世纪七十年代就已提出,并由国外的MTS、Schenk等公司推广。国内对道路模拟试验技术的研究起始较晚,主要集中在控制理论、耐久试验方法方面,如2002年清华大学的杜永昌[1]等人研制了汽车道路动态试验模拟控制系统,2012年合肥工业大学的钱立军、吴道俊[2]等人对道路模拟加速试验技术展开了研究,2013年同济大学的胡毓冬、周鋐[3][4]等人对汽车室内道路模拟试验的控制算法进行了相关研究,而对实际试验中各项参数的影响分析较少。
一般的道路模拟试验步骤包括:①道路载荷谱采集,获取目标信号;②求解系统频率响应函数矩阵;③生成初始驱动信号;④通过迭代对驱动信号进行修正,直到模拟精度达到要求;⑤编辑试验驱动谱,对样车/样件进行试验。
轴耦合道路模拟是目前最先进的道路模拟试验技术,迭代环节是其达到高精度要求的关键。本文基于MTS公司的329型6自由度通道轴耦合道路模拟试验系统(下称二十四通道),选择不同控制信号作为迭代目标、调整不同的车辆状态,对各参数在台架驱动谱迭代过程中的影响展开研究。
1 获取目标信号
1.1 道路载荷谱采集
为使车辆在道路模拟试验中快速高效地达到与用户使用相当的可靠性验证效果,道路载荷谱采集一般在试验场进行,采集信号包括控制信号和监测信号。
控制信号在道路模拟试验中是用于驱动谱迭代的目标信号(即远程控制参数),其台架模拟响应与实际道路响应的误差一般要求小于20%,选取原则[5]为:①尽可能与某一试验驱动力成线性关系而与其它试验驱动力成正交关系,便于迭代快速收敛。②若有需要重点关注的监测信号信号采集点,可选择靠近监测信号采集点,以便监测点处的道路模拟疲劳损伤接近实际道路损伤。
监测信号主要是用于监控车辆危险点和试验需求关注的位置,其选取主要根据仿真结果和试验经验进行。
对于整车道路模拟试验,控制信号可以选择车轮六分力、轴头加速度、悬架位移或弹簧应变等,监测信号可以选择车身塔座/质心加速度、稳定杆应变、转向拉杆应变等,根据试验具体情况而定。
1.2 信号处理
由于车辆行驶时响应频率50Hz以上的部分在损伤计算时占总损伤比例较小,因此疲劳耐久分析中主要关注50Hz以下频段。根据采样定理,信号采样率一般设置需500Hz以上,保证采集信号的幅值无损失。每个工况在额定车速和载荷条件下连续采集不少于5组数据,采用损伤归一求模的方法对每组数据控制信号通道进行计算,选择损伤中位样本,经滤波、去毛刺、去均值、去趋势值、去除连接路处理后作为道路模拟试验目标谱信号。
2 求解传递函数
道路模拟试验台与车辆组成闭环控制系统,系统输入即台架驱动信号X(x1,x2,x3,…),包括各向力/力矩信号和位移/角度信号;输出为车辆响应信号Y(y1,y2,y3,…)。
2.1 激励信号
采用白粉红噪声对车辆系统进行激励,根据目标信号主要频率范围设置激励信号的上下截止频率,通常为50Hz和0Hz。可添加形状曲线对激励信号高频部分进行衰减,如图1所示。对于整车试验,拐点频率可选择0.6Hz(图中虚线),力/力矩通道衰减指数取1~1.5,位移/角度通道衰减指数取1.5~2。各通道时域幅值范围根据目标信号关联通道幅值分别设定。
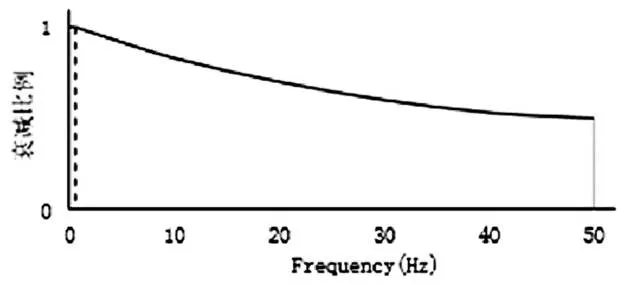
图1 激励信号频率过滤形状曲线
2.2 获取频率响应函数矩阵
在播放白粉红噪声激励X获得响应信号Y后由H估算法获得系统的频率响应函数矩阵。H估算法有两种,如式(1)和式(2):


式中,H1、H2为系统FRF矩阵,Gyx为系统激励和响应的互功率谱矩阵,Gxx为系统激励的自功率谱矩阵,Gyy为系统响应的自功率谱矩阵,Gxy为Gyx的转置。
对于完全线性系统,两种算法等效。但台架-车辆属于非线性系统,在实际运行过程中,H2响应往往包含比激励更多的噪声成分,H2在计算时受噪声影响高于H1。综合考虑,本文采用H1算法计算FRF矩阵。
FRF模型对系统描述的准确程度可由激励、响应之间的相干函数矩阵来评价:
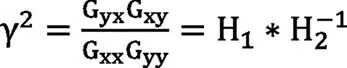
式中,γ为激励X和响应Y之间的相干函数矩阵,一般γ2大于0.8则可认为相干性较好。
3 数据迭代
道路模拟试验系统输入、输出与频率响应函数的关系式为:

式中,X(jω)、Y(jω)分别为系统输入X(t)、输出Y(t)的傅里叶变换。
由于系统非线性,本文采用频域迭代的方式来获取逐步收敛的驱动信号,使控制信号逼近对应的目标信号,迭代流程如图2所示。
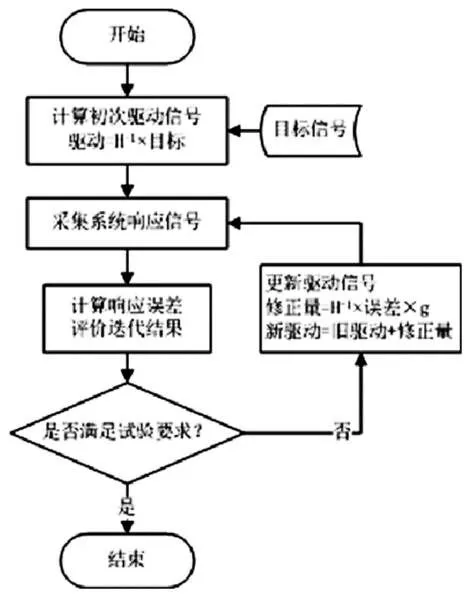
图2 迭代流程
通常系统响应信号的通道数与驱动信号相同,其频率响应函数矩阵H是一个方阵。初次驱动信号的计算为:

式中,X0(jω)为初次驱动信号X0(t)的傅里叶变换,Yd(jω)为目标信号Yd(t)的傅里叶变换。
若系统响应信号与驱动信号通道数不同,一般是响应信号通道数多于驱动信号,可用最小二乘的方法求得初始驱动信号:

由于非方阵计算存在拟合误差,所以根据驱动信号情况选取响应通道,采用式(5)计算更容易得到高精度的计算结果。
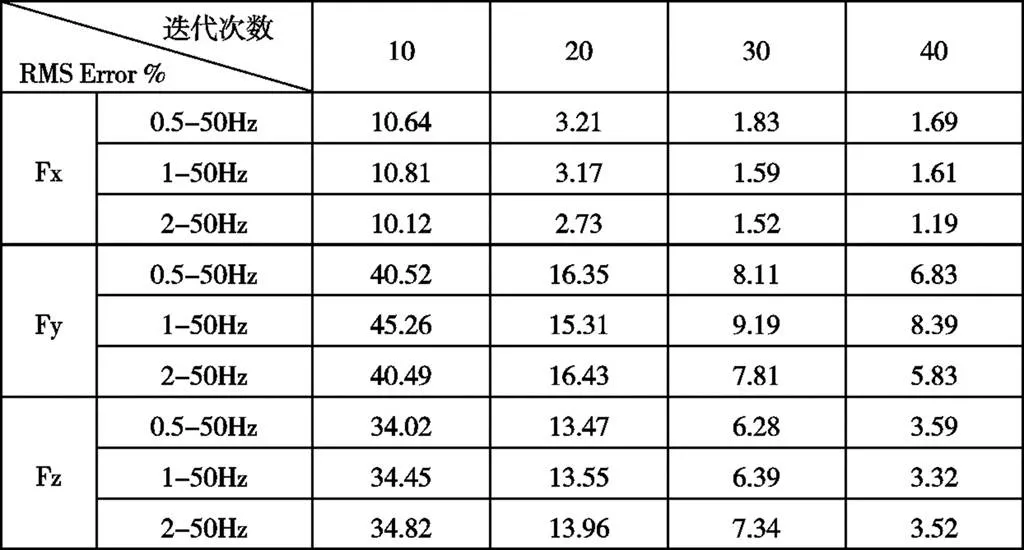
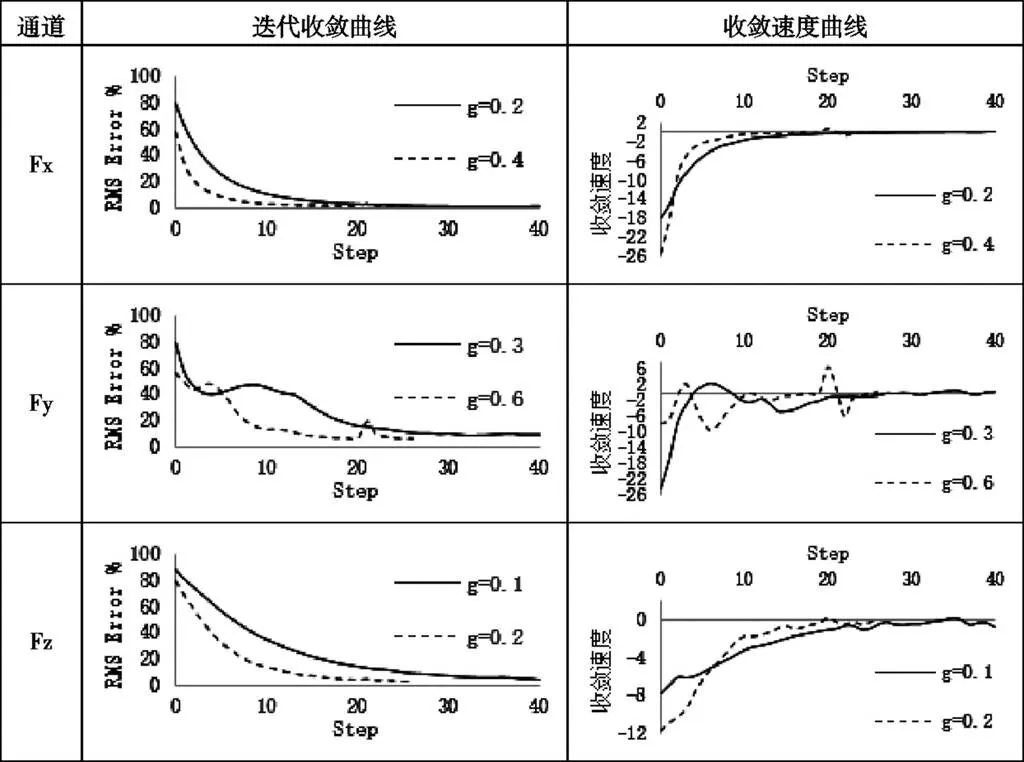
对于非线性系统,由目标信号和系统的频率响应函数直接求解可能会导致驱动信号不准确,过大的驱动信号甚至会损坏试验设备和车辆,而且容易导致迭代过程发散,为了防止这类情况,一般在求解驱动信号时添加增益因子g(0 播放驱动信号获得系统的实际响应信号,进而得到各响应信号与目标信号的实时误差e(t)。采用迭代时响应信号相对目标信号的均方根误差RMS Error对迭代结果进行评价,计算如下: 后续驱动信号可由实时误差计算获得: 式中,ΔX(jω)为迭代过程中驱动信号矩阵的修正量,E(jω)为实时误差e(t)的傅里叶变换,Xi(jω)、Xi+1(jω)分别为第i步、第i+1步驱动信号的傅里叶变换,通过对Xi+1(jω)的傅里叶逆变换可获得下一步驱动的时域信号。其中,加权系数g可根据每一步迭代的实际情况进行调整,通常在迭代开始时取值较小,随着迭代次数增加逐渐增大。 一般情况下,在二十四通道道路模拟试验中,各通道RMS Error值均小于20%即可认为满足试验需求。RMS Error值越小,迭代结果响应越接近目标信号,模拟精度越高。 日常试验中,影响迭代结果的参数主要有两大类: (1)RPC系统参数,包括控制信号、迭代过程调节参数等,这些参数的选择决定了驱动信号的计算结果。 (2)车辆状态参数,包括车辆的载荷、悬架减振器/衬套的温度等,这些参数直接影响车辆系统的响应。 二十四通道整车道路模拟试验驱动信号包括17个力/力矩和7个位移/角度信号,响应信号根据试验情况选择,通常是四个车轮的六分力信号,可根据需求增加悬架位移、车身加速度等作为监测信号。 表1 垂向控制信号迭代结果对比 根据信号选取原则,选取相关性较强的车轮垂向力、轴头垂向加速度、悬架位移作为研究对象,三种信号采集点如图3。先后以三种信号之一作为垂向迭代控制信号,其余信号作为参考,迭代至相对均方根误差RMS Error≤10%。根据线性累积损伤(Miner)法则,计算前轴垂向响应信号与目标信号的伪损伤比[6]如表1。 结果表明,台架上使用垂向力作为控制信号进行迭代时,轴头垂向加速响应的伪损伤要比目标值小约30%;反之以垂向加速度作为控制信号进行迭代,垂向力的伪损伤要比目标值比目标值大约30%;当以悬架位移作为控制信号进行迭代时,垂向力和加速度响应都要比目标值大。 由于力信号的频率分布范围更广更均衡,频谱曲线可看作加速度和位移的结合,在反映目标信号时更全面;而加速度、位移信号因为主频较为单一集中,远离主频的区域幅值较小,会造成一定程度的信号丢失。所以在同样的车轮载荷输入下,加速度、位移信号与路面实际响应相比会出现计算损伤稍微偏小,更适合作为监测信号。 迭代过程调节参数主要有控制频段和增益因子。迭代控制频段实质是驱动谱求解过程中各信号通道用于计算的频段,决定迭代结果驱动信号的频率分布;增益因子即求解每一步驱动信号时加入的加权系数g,对迭代的收敛速度有直接影响。 4.2.1控制频段 车辆行驶载荷谱由两部分组成,一部分是由车辆的变速、转向、制动等人为驾驶因素引起的,信号频率一般在0.6Hz以下,属于低频信号;另一部分由道路条件引起,信号频率一般在0.6Hz以上,属于高频信号[7]。低频信号往往伴随着该信号方向上较长时间的作动位移,台架行程难以达到;而高频信号50Hz以上频率幅值几乎为零,损伤很小,通常不作可靠性耐久分析。 本文以车轮六分力为控制信号,对道路载荷目标信号进行了不同控制频段设置,分析流程如图4: 图4 控制频段分析流程 以左前轮三向力Fx、Fy、Fz为例,各信号通道频率谱如图5: 图5 目标信号左前轮三向力频谱 迭代至RMS Error≤10%,结果响应的伪损伤统计如表2。其中,损伤比为响应信号伪损伤与目标信号伪损伤的比值。 表2 迭代结果响应损伤 由于目标信号Fy、Fz频率在2Hz附近幅值较大,采用2~50Hz控制频率迭代时,Fz响应的损伤降低较明显,Fy次之,而0~1Hz频段的控制与否对结果影响不大。 表3 不同控制频段收敛对比 统计迭代过程中左前轮三向力信号收敛情况如表3所示,不同控制频段对迭代收敛情况几乎无影响。 4.2.2增益因子 设置各通道控制频段为1~50Hz,增益因子g取两组固定值分别进行迭代,对目标信号左前轮三向力迭代收敛曲线(RMS Error曲线)求导获得收敛速率曲线,见表4。 由表中曲线看出,取值较大的第二组增益因子使得迭代收敛速率明显快于第一组,但也存在一些不稳定情况,侧向力Fy的收敛速率波动较大,发散风险相对较高。 表4 不同增益因子收敛对比 车辆作为系统的输出端,其状态参数直接影响着迭代的结果响应,在既定的目标信号迭代过程中,车辆状态的变化会反映到驱动信号的计算结果;相同的驱动信号也会因为车辆状态的改变响应不同,而影响后续迭代的计算。 4.3.1车辆载荷 车辆载荷作为试验过程中重点把控的因素,通常在试验标准规范类文件中有明确规定,但在实际情况中因配置的差异、样车本身的装配情况,往往与目标值存在偏差。 表5 车辆装载质量分布 为最大化验证车辆载荷对试验迭代结果的影响,分别选取满载、半载、空载三种形式的车辆配载进行迭代,各配载载荷分布情况如表5所示。以车轮六分力为控制信号,迭代至收敛速度为0(RMS Error≤10%),获得三种载荷对应的驱动信号,计算各通道伪损伤并以满载驱动信号损伤为基准归一化,结果如图6所示。 结果显示三组驱动信号大部分通道损伤差异不大,损伤比在[0.5,2.0]区间。其中纵向通道差异较小,垂向和侧向差异稍大;随着载荷的减少,垂向和侧向驱动信号逐步增大。可见配载对试验迭代结果有影响,但并非很大,在载荷差异不大(装载质量±10%)的同车型不同配置或者衍生车型道路模拟试验中是可以接受的。 图6 不同载荷迭代驱动信号损伤比 4.3.2减振器温度 减振器温度与悬架状态息息相关,是道路模拟试验中容易忽略的一个因素。在迭代过程中,由于操作的不连贯,系统运行与暂停时,都会引起减振器的温度升高或降低,而温度与减振器阻尼非线性负相关,从而引起悬架力响应的变化。本文使用同样的驱动谱,在减振器温度为室温(26℃)和高温90(℃)时分别激励系统,获得四个车轮六分力响应信号,计算伪损伤对比(室温状态响应损伤/90℃状态响应损伤)如图7。 图7 不同减振器温度系统响应损伤比 可见减振器温度升高,由于阻尼降低,在同样的激励下车辆系统的响应会减小。所以在进行驱动谱迭代前,先对系统进行预热,让车辆各系统进入试验状态,同时迭代过程中保持运作的连贯性,减少每一步迭代数据处理用时的差距,可以使得迭代收敛更顺畅,结果精度更高。 本文从RPC系统和车辆系统两方面对道路模拟试验迭代过程中实际遇到的几大主要影响因素进行了分析,获得结论如下: (1)在迭代控制信号的选取方面,力、加速度、位移信号均能达到较好的迭代结果。其中力信号由于其包含的频率范围更广更均衡,更适合作为控制信号;而加速度、位移信号更适合作为试验过程监测信号。 (2)控制频段可以消除目标信号中人为驾驶因素等的影响,但不能提升迭代收敛速率;迭代收敛速率受增益因子影响明显,但增益因子过大会增加迭代过程不稳定。 (3)使用同样的目标信号迭代求解驱动谱时,车辆载荷越小计算获得的驱动信号越大,侧向和垂向通道较为明显,但大部分驱动通道的偏差均在可接受范围内。 (4)在减振器工作适用温度范围内,同样的驱动输入,车辆悬架减振器温度越高,其响应越小。迭代过程中保持车辆零部件的状态稳定性,可以减小收敛的波动。 [1] 杜永昌.车辆道路模拟试验迭代算法研究[J].农业机械学报,2002, 33(2):5-7. [2] 吴道俊.车辆疲劳耐久性分析,试验与优化关键技术研究[D].合肥:合肥工业大学, 2012. [3] 胡毓冬,周鋐,徐刚.整车道路模拟试验台的控制算法[J].同济大学学报,2012,40(8):1244-1248. [4] 胡毓冬,周鋐,徐刚.整车道路模拟虚拟试验台研究[J].汽车工程学报,2014,4(2):137-142. [5] 张觉慧,金锋,余卓平.道路模拟试验用载荷谱样本选择方法[J].汽车工程,2004,26(2):220-223. [6] 周德泉,李航,李开标,等.轴耦合整车道路模拟试验与道路试验关联性检定[J].工业技术创新,2017,4(3):78-81. [7] Li Yung Lee. Fatigue testing and analysis[M].New York:Elsevier Butterworth Heinemann,2005:30-40. Key parameters analysis of spindle-coupled road simulation test Li Hang, Zhou Dequan, Li Kaibiao, Chen Yu, Liu Jianwen ( Guangzhou Automobile Group Co., Ltd., Guangdong Guangzhou 511434 ) Based on the 6-dof spindle-coupled road simulation system, the basic principle of the road simulation test is introduced. Researching on the main parameters of the test system and the vehicle system,the results of pseudo damage calculation and spectrum analysis shows that different control signals, control band, vehicle load and shock absorber temperature have different effects on the test results. road simulation; iteration parameter; controlled signal A 1671-7988(2019)05-74-05 U467.5 A 1671-7988(2019)05-74-05 U467.5 李航(1987-),男,广东阳春,汉族,硕士,工程师,主要研究方向为整车/零部件道路模拟、数据采集测试。 10.16638/j.cnki.1671-7988.2019.05.022
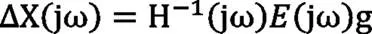

4 迭代参数分析
4.1 控制信号

4.2 过程调节参数



4.3 车辆状态参数



5 结论
