不一样的冒泡排序

陈凯

冒泡排序是一种著名的排序算法，虽然效率不高，但这种排序方法有着它自身的独特性：它和大部分人类习惯的排序方法不同，但对于机器来说，却反而是比较容易实现的。初次遇见冒泡排序的学习者，往往会被循环嵌套的代码弄晕。本文从几个简单的小游戏入手，由简入难，逐步展现出使得数据排序得以自动进行的关键思路。

上升的气球与受限的工作空间

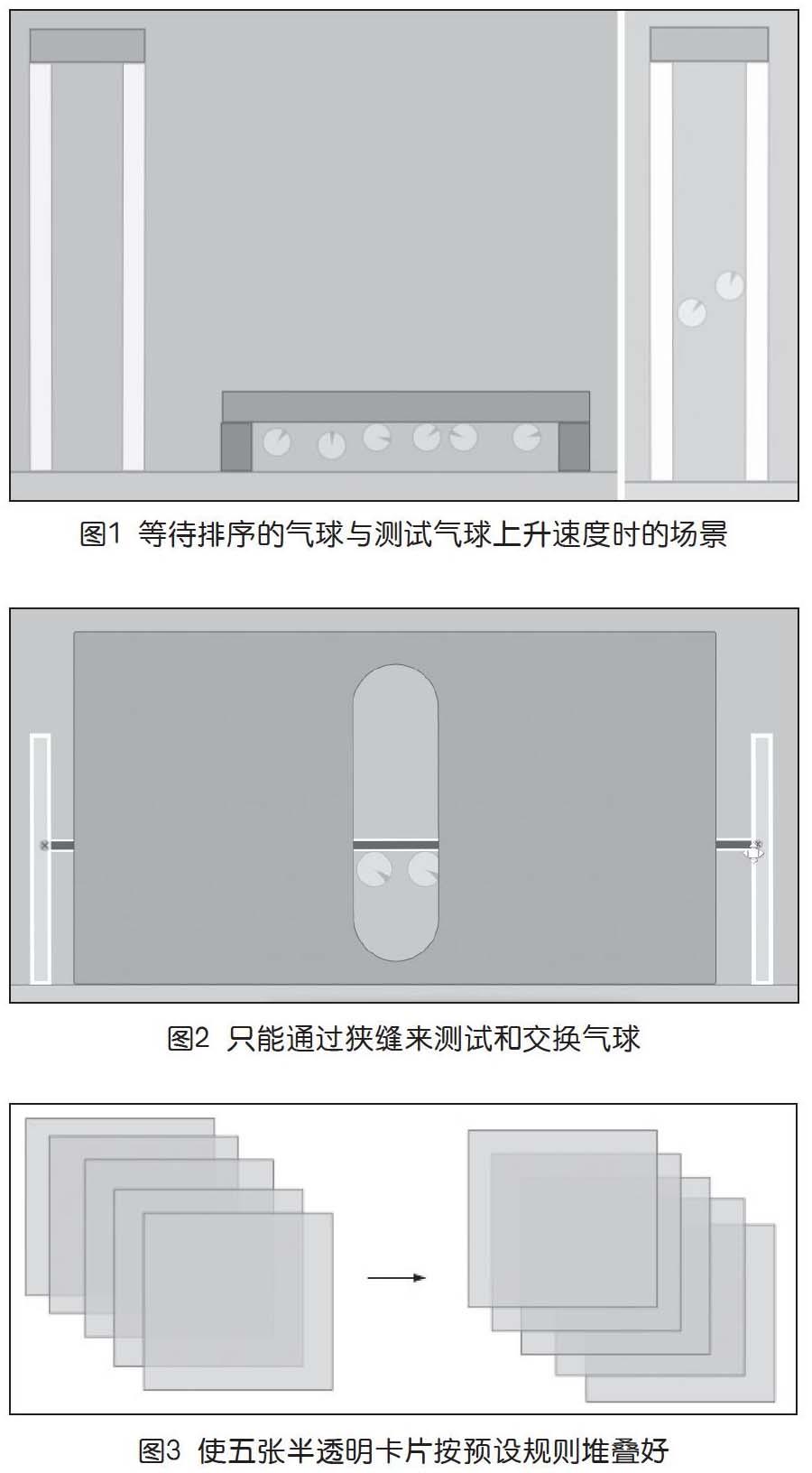
Algodoo是一个仿真物理沙盒软件，用这个软件可以轻松地创造出排序任务情境。例如，给出若干个密度不一样的气球，按它们的上升速度进行排序，如图1所示。在Algodoo场景中，可以看出气球都被放置在一个矩形盒子中，以免飘走，而测试气球的竖立轨道每次只能容纳两个气球进行测试。这样设计场景的意图是，其一，无法直接看出被比较物体的大小顺序，必须测试后获得结果；其二，测试轨道空间有限，用来比喻冒泡排序所需要的不大的存储空间。

在这个气球测试场景中，虽然气球上升测试窗口受限，但气球选择的顺序却是不受限制的，所以可以进一步优化场景，使得其和冒泡排序程序实现过程更加相像。比如，可以制作一个带狭缝的挡板，抬起挡板后侧的栏杆，就可以在狭缝中观察气球的上升速度，然后根据上升速度重新调整气球位置，如图2所示。不过因为狭缝空间小，每次只能交换相邻气球的位置，可以将那个狭缝看作是机器在进行冒泡排序时的“视角”和“工作空间”，用以印证冒泡排序所需要的很低的空间复杂度。

堆叠的卡片与流程化的比较交换过程

对若干数量并不多的数据排序时，人眼往往很快就能找出其中的最大值或最小值，但机器是不会自动拥有这种直观能力的，所以在学习冒泡排序时，就先要假装自己看不出谁大谁小，这种“假装不知道”的操作会对初学者产生一定困扰，不妨设法让学习者从假装不知道，变成真的不知道，还原出机器所面临的问题。

例如，有这么一个任务，在演示文稿中，有五张不同大小的卡片堆叠在一起（如上页图3），要求对卡片只能使用“下移一层”和“置于底层”操作，并且只能对最上面的一张卡片进行操作，任务目标是将卡片的排列方式变化为从右下到左上角层层堆叠。为了能够看出卡片相互之间的关系，每张卡片是半透明的，即便如此，当卡片比较多，堆叠又随机乱序的情况下，若想要快速完成任务，并没有想象中那样简单，不仅需要眼力和耐性，还要一些小小的诀窍。

卡片稍微多一些，操作者难免会眼花目眩，可以借用冒泡排序的思路，让排序过程变得“傻瓜化”。以五张卡片为例，每次只比较最上面一张和最上面第二张的卡片次序是否正确，如不正确，则将第一张卡片“下移一层”，然后将剩下的最上面的卡片“置于底层”；如次序正确，则只要将当前最上面的卡片“置于底层”即可。假如有五张卡片，那么先比较四次，然后无条件执行一次“置于底层”，接下来，再比较三次，然后无条件执行两次“置于底层”，接着，比较两次，无条件执行三次“置于底层”，最后再比较一次即可完成排序任务。这恰好就对应着冒泡排序的比较过程，对于n个数据冒泡排序，第1轮需要比较n-1次，第2轮需要比较n-2次，直到第n-1轮只要比较1次。

这里有一项更困难些的任务，若卡片形状相同，面积不同，要求将堆叠在一起的所有卡片的外部边缘显露出来，规则仍然是只能对最上面的卡片进行操作，并且只能执行“置于底层”和“下移一层”操作，如图4所示。当卡片比较多的时候，只凭眼力和记忆完成任务，是颇有困难的，但若借用冒泡排序的方法，按流程机械性地进行比较和交换，虽然耗时比较长，但肯定可以完成任务。

滑动的标尺与数学模型

以上几个游戏都实际体验过之后，再回头来看冒泡程序的代码，是不是感觉代码变得简单了呢？接下来不准备介绍大家都已经非常熟悉的传统的冒泡排序程序代码，而是试着来完成一段有点小小奇葩的代码：既用不到传统冒泡排序代码中的嵌套循环，也不用两两比较数据大小，却能完成冒泡排序。

一般来说，冒泡排序需要一个一维的数组空间，可以用一个一行n列的表格及若干数字来演示比较和排序过程。但若用一把尺子和若干标记，也是可以实现冒泡排序的。

假设等待完成排序的数字是[3，2，6，4，5]，在尺子0厘米和3厘米处标记号，两个记号之间的距离正是3，代表等待排序的第一个数据；接着在5厘米处标记号，5厘米处记号与3厘米处记号距离是2，代表等待排序的第二个数据……以此类推，于是在尺子的0厘米、3厘米、5厘米、11厘米、15厘米、20厘米处共标了6個记号。相邻记号之间的距离就代表了等待排序的数字。接下来，一次看三个标记，把左宽右窄的标记摆放成左窄右宽的样子即可，如上页图5所示。当全部标记均满足左窄右宽规则时，排序就完成了，如上页图6所示。

这种方法在程序实现中，乍看上去似乎都不需要做比较大小的判断，笔者给出的程序代码中，借用了一个绝对值函数，就实现了将左宽右窄的标记摆放成左窄右宽的功能。并且，代码前半段直接生成了等待移动的标记序号，所以也用不到在循环结构中嵌套循环结构。等待排序的数字是[6，5，4，3，2]，对应到尺子上的标记，就是0厘米、6厘米、11厘米、15厘米、18厘米、20厘米这6个标记。所生成等待移动的标记序号就是[1，2，3，4，1，2，3，1，2，1]，很显然，0厘米位置的标记和20厘米位置的标记不需要移动，因为第一轮最多需要移动4次标记，第二轮最多移动3次标记，第三轮最多移动2次标记，第四轮最多移动1次标记，总共是移动10次标记。当标记很多的时候，可以利用数学公式“首项加末项乘项数除以二”来得到所需要的最多移动次数。程序代码和运行结果如图7所示。

这样，就实现了一个既没有大小比较，又没有循环嵌套结构的冒泡排序程序代码。希望学习者能通过这个例子，感受到数学模型和数学方法对于解决某特定信息技术任务的重要作用。