基于Matlab的有理曲线拟合在数据预测中的应用
2019-03-20凌雪岷潘娟娟
凌雪岷,潘娟娟,李 宁
(1.安徽新华学院通识教育部,安徽合肥230031;2.淮南师范学院金融学院,安徽淮南232038)
如今网络越来越发达,数据越来越丰富,不知不觉我们进入了所谓的大数据时代,在大数据时代数据的最大价值依然还是预测分析。在数学建模中,数据预测模型有灰色模型、Logistic模型等[1-2]。而对于数据的处理,多数采用的是多项式拟合的方法[3]。表1给出了某市2011-2015年城市、镇和乡村中15~49岁育龄妇女生育率数据,利用这些数据建立生育率随年龄、时间变化模型,借助Béizer基函数,再用有理曲线代替多项式曲线对数据进行拟合,作出相应的曲线图。由点及面,建立全国育龄妇女生育率模型,用数据说明有理曲线较多项式曲线拟合度更为优良。
1 模型建立
1.1 2011-2015年某市育龄妇女生育率随年龄、时间变化模型
首先借助Matlab软件[4],用6次多项式拟合2011-2015年某市育龄妇女生育率随年龄变化的数据,其中yi(i=1,2,3,4,5)表示2011-2015年某市育龄妇女随年龄变化的生育率,结果如下:
2011年某市育龄妇女生育率随年龄变化函数(见图1)为

2012年某市育龄妇女生育率随年龄变化函数(见图2)为
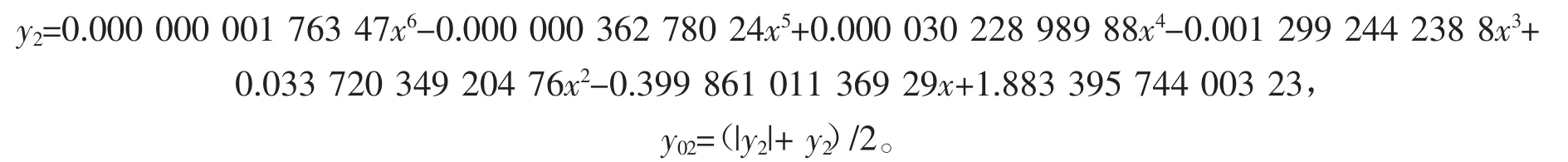

表1 某市2011-2015年育龄妇女生育率数据
2013年某市育龄妇女生育率随年龄变化函数(见图3)为
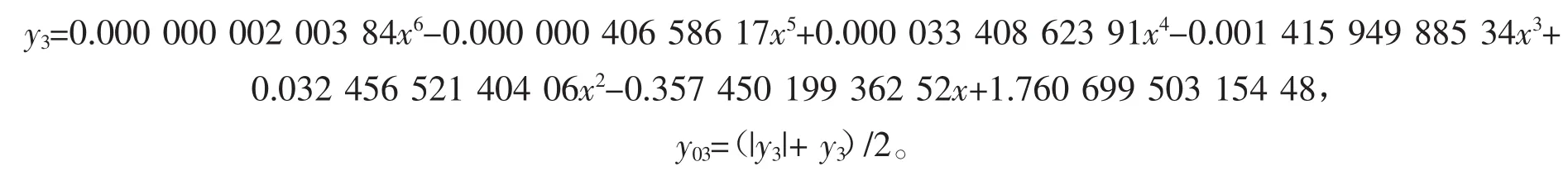
2014年某市育龄妇女生育率随年龄变化函数(见图4)为
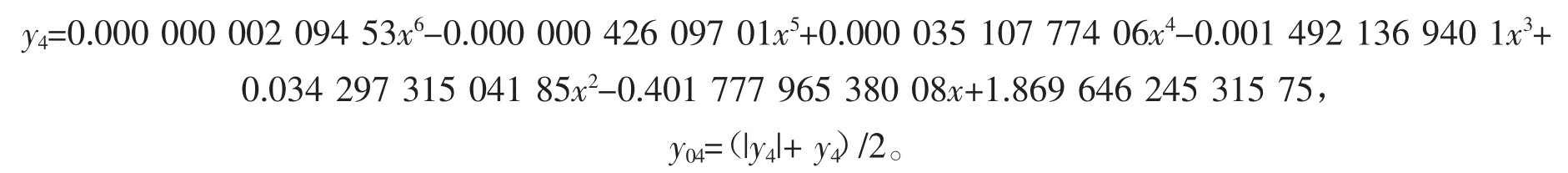
2015年某市育龄妇女生育率随年龄变化函数(见图5)为
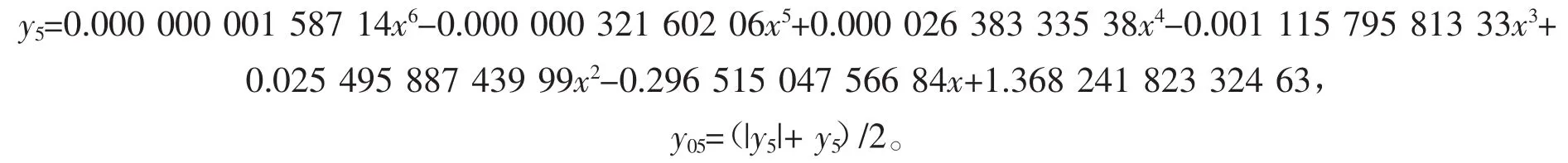
借助于Béizer基函数构造出2011-2015年某市育龄妇女生育率随年龄和时间变化函数模型为

B0,B1,B2,B3,B4为变形后的 Béizer基函数。
利用Matlab软件,结合以上函数画出2011-2015年某市育龄妇女生育率随年龄变化图以及该市育龄妇女生育率随年龄和时间的变化图(见图6)。
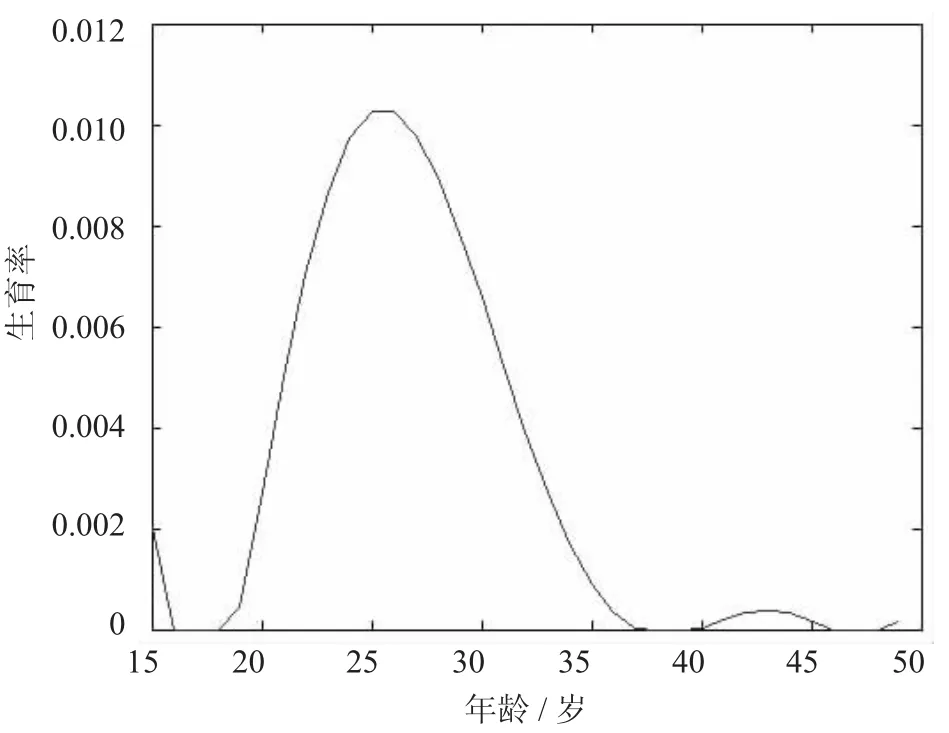
图1 2011年生育率随年龄变化图
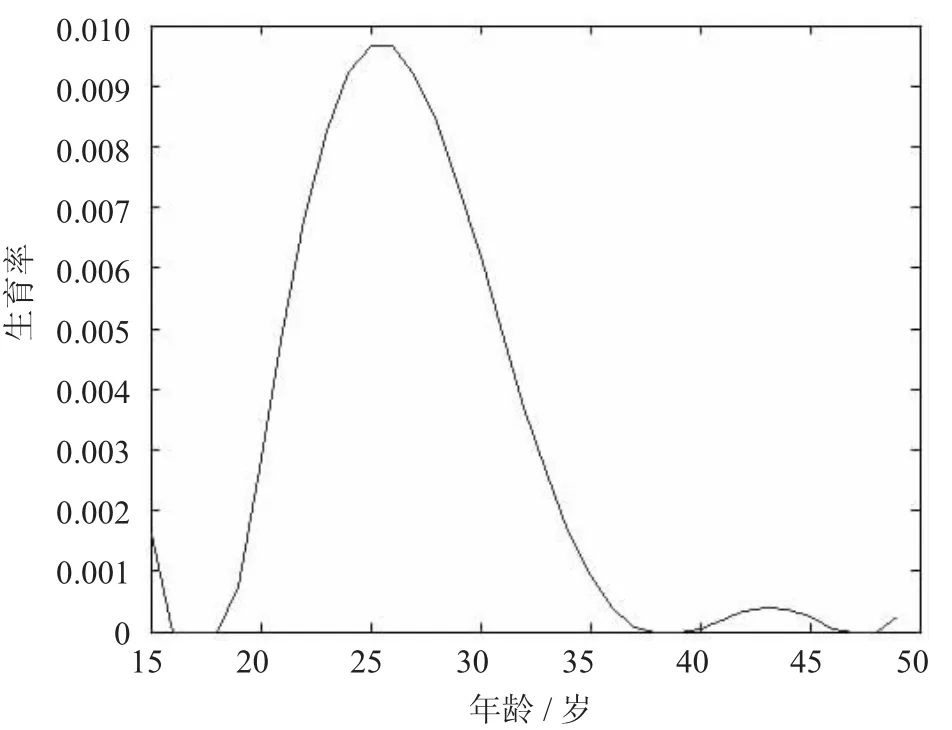
图2 2012年生育率随年龄变化图
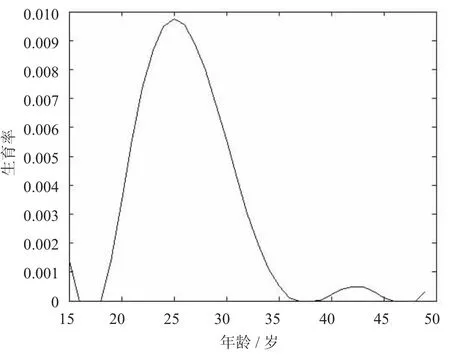
图3 2013年生育率随年龄变化图
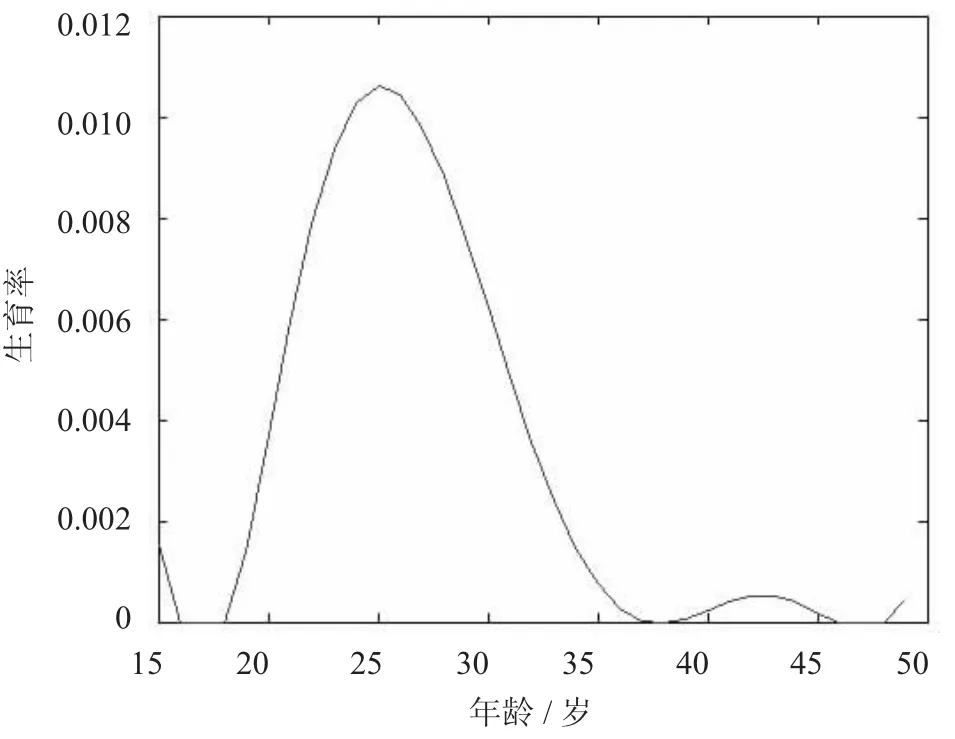
图4 2014年生育率随年龄变化图
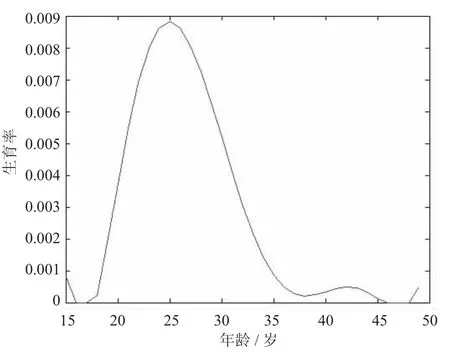
图5 2015年生育率随年龄变化图
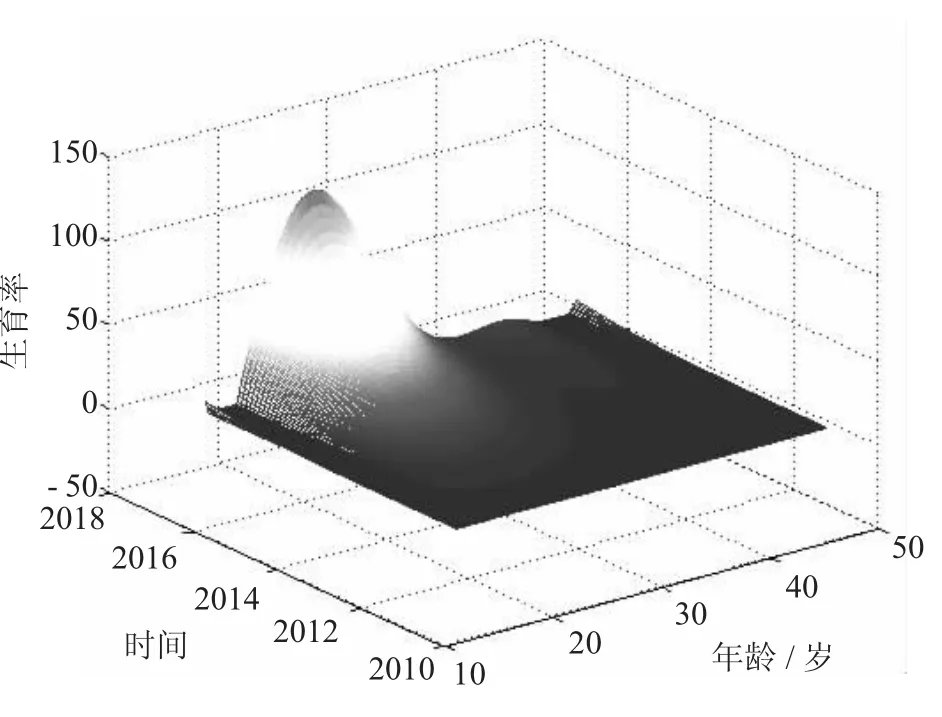
图6 2011-2015年生育率随年龄和时间的变化图
说明:(1)图6表示该市育龄妇女生育率随年龄和时间总的变化曲线。
(2)由于2013年数据异常,所以出现图6中间下陷情况。
1.2 2011-2015年全国育龄妇女生育率随时间变化模型
利用表1给出的某市育龄妇女生育率数据,由点及面,可以预测全国育龄妇女生育率随时间变化的趋势。
通过散点图的走势我们用有理曲线拟合,具体过程如下:
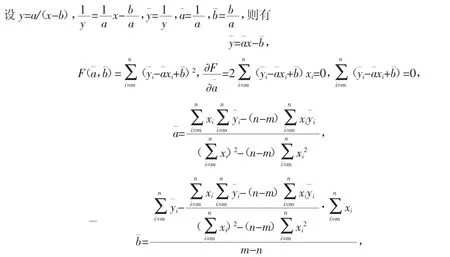
其中,xi是第 i年,是第i年育龄妇女生育率。
根据以上模型,计算出全国城市、城镇、乡村育龄妇女生育率随时间变化函数。
城市育龄妇女生育率随时间变化的函数为
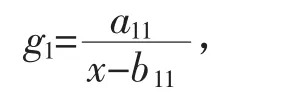
其中,a11=1 058.929 108 684 027,b11=1 978.722 921 156 550。
城镇育龄妇女生育率随时间变化的函数为
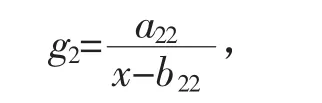
其中,a22=1 519.870 748 344 614,b22=1 958.548 172 859 424。
乡村育龄妇女生育率随时间变化的函数为
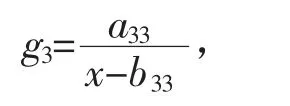
其中,a33=1 058.929 108 684 027,b33=1 978.722 921 156 550。
由于全国城市、镇、乡育龄妇女在各年全国育龄妇女比例不同,我们有必要确定权函数,根据表1中的数据,用有理曲线拟和出城市、城镇、乡村育龄妇女在各年全国育龄妇女比例随时间的变化曲线模型。
结合表1的数据和Matlab软件,计算出以下结果:
全国城市育龄妇女占全国育龄妇女比例函数为
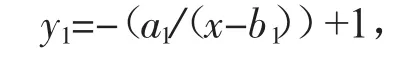
其中,a1=65.118 666 767 592 67,b1=1 914.885 798 109 688。
全国城镇育龄妇女占全国总育龄比例函数为
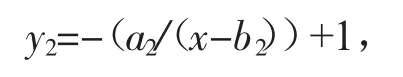
其中,a2=64.632 630 658 907 94,b2=1 927.170 994 739 364。
全国乡村育龄妇女占全国总育龄比例函数为
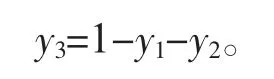
把城市、城镇、乡村育龄妇女生育率随时间变化函数与权函数进行加权得到全国育龄妇女生育率随时间变化模型,即:h=y1g1+y2g2+(1-y1-y2)g3。
利用以上函数,可以计算出城市、城镇、乡村的人口更替水平分别是2035年、2040年、2050年,全国的人口更替水平是2037年。
本文仅以生育率为例,说明有理曲线在数据拟合方面的实际应用,考虑到2016年二胎政策放开,所以该模型并不适用于人口预测。
2 结语
通过上述例子发现,借助于Béizer基函数,构造育龄妇女生育率随年龄和时间变化的曲面图,固定一个变量,可以看出另一个变量的变化情况。同时,可以总体直观看出生育率与年龄和时间的关系。利用有理曲线代替多项式曲线对数据进行拟合,提高了拟合的精度。有理曲线目前已经越来越多地应用到几何造型、经济等方面,其作用也是深远的。
