基于检测算子经验学习鱼群算法的移动机器人路径规划
2019-03-20黄宜庆刘晓峰
王 徽,黄宜庆*,刘晓峰
(1.安徽工程大学 电气工程学院,安徽 芜湖 241000;2.芜湖发电有限责任公司,安徽 芜湖 241000)
移动机器人路径规划问题在现实生活中具有重要的研究价值.路径规划问题一般分为全局路径规划和局部路径规划问题,前者为环境参数全部已知,后者为部分环境参数已知.在自动驾驶、无人机自主飞行等领域有重要的应用价值和研究意义.
目前,移动机器人路径规划的热点方法主要有群智能算法的路径规划方法[1],包括人工鱼群算法、深度强化学习算法[2]、蚁群算法[3]等;文献[4]中在移动机器人路径的起始点和目标点之间输入角度值的模糊推理系统.算法在完成路径规划中耗时短,但是对于静态环境的要求较高,需要建立完善的知识库,因而耗费较多的存储空间和时间;文献[5]中提出将基因算法和自适应模糊逻辑算法应用到移动机器人路径规划问题上,通过遗传算法生成一条从起始点到目标点的可行路径,再利用Hermite插值多项式使路径平滑,最后通过自适应模糊逻辑控制器让移动小车跟随该路径.算法在应用过程中小车行走路径表现效果较好,但是路径规划结果存在早熟现象,且不能有效地摆脱路径中的陷阱,会出现陷入局部极值的问题;文献[6]中提出将粒子群优化算法用来解决路径规划问题,通过设定必要的中间目标来提高算法执行效率.算法在复杂地图环境中的表现效果较好,但是中间目标点的选取方式导致路径规划存在路径冗长问题;文献[7]中提出使用简化群体优化算法解决移动机器人路径规划问题.算法对于机器人路径规划的效果较好,但是该算法应用的环境模型较为简单,在较为复杂的环境中效果不再突出,并且对于机器人可通行的区域限制条件不足;文献[8]中提出使用混合策略改进传统人工鱼群算法固定不变的步长和视野范围来解决移动机器人路径问题.算法在移动机器人路径规划上效果较好.但是在较为复杂的地图环境中时,会出现次优解干扰全局路径和理性的问题;文献[9]提出动态分级的蚁群算法,在原始蚁群算法中加入了狼群算法的分级机制.算法提高了传统蚁群算法的执行效率,但是对于较复杂地图环境中存在的较多陷阱,不具备逃逸能力,最终无法完成路径规划任务;文献[10-11]提出了蚁群算法的优化改进策略,针对传统蚁群算法易于陷入局部最优解的问题做出改进.算法在二维地图环境中表现出具备逃逸陷阱的能力,但是存在路径冗长的问题.
传统人工鱼群算法是目前仿生算法中收敛速度和寻优效果较好的算法[12],而模糊逻辑算法在建立好静态环境模型后,完成路径规划也具有较好的收敛速度.基于鱼群算法主要解决次优解干扰全局路径合理性问题和路径冗长问题,使得算法具备在复杂多陷阱地图环境中具备逃逸能力,同时规划的路径曲线长度最优.研究设计了经验学习的方法,使得原来不具备学习能力的鱼群拥有了学习错误经验的能力,解决了次优解干扰全局路径和理性的问题,同时具有较好的摆脱陷阱的能力;针对路径冗长问题,研究设计了优化检测算子,基于检测算子设计的优化算法,极大地减少了路径的长度.通过仿真与其他算法的比较说明了算法的优越性、可靠性和稳定性.
1 栅格环境化的鱼群算法
选择栅格法搭建移动机器人的行走环境.以xoy平面建立坐标系,在以单位1作为机器人移动步长,建立栅格环境.其中黑色栅格代表障碍物,白色格子代表机器人可以移动的区域.为了适应栅格环境下的机器人路径规划问题,需要对于传统人工鱼群算法做如下定义.设每个栅格为1*1的正方形格子.

定义2:用Allow表示移动机器人的可行域,用Barrier表示障碍物区域.整个区域,用s表示,满足Allow∪Barrier=S,(Allow)c∩S=Barrier,(Barrier)c∩S=Allow.
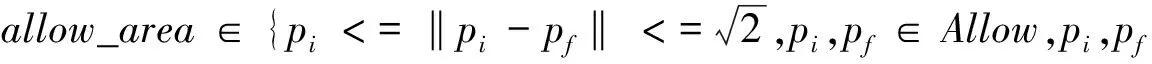
定义5:鱼群觅食行为,设pi为当前鱼群的位置,Hi为当前人工鱼pi处的食物浓度,pk为pi可行域中的任意一个位置,由鱼群的随机行为决定,Hk为pk处的食物浓度,则觅食行为函数可描述如下:
(1)
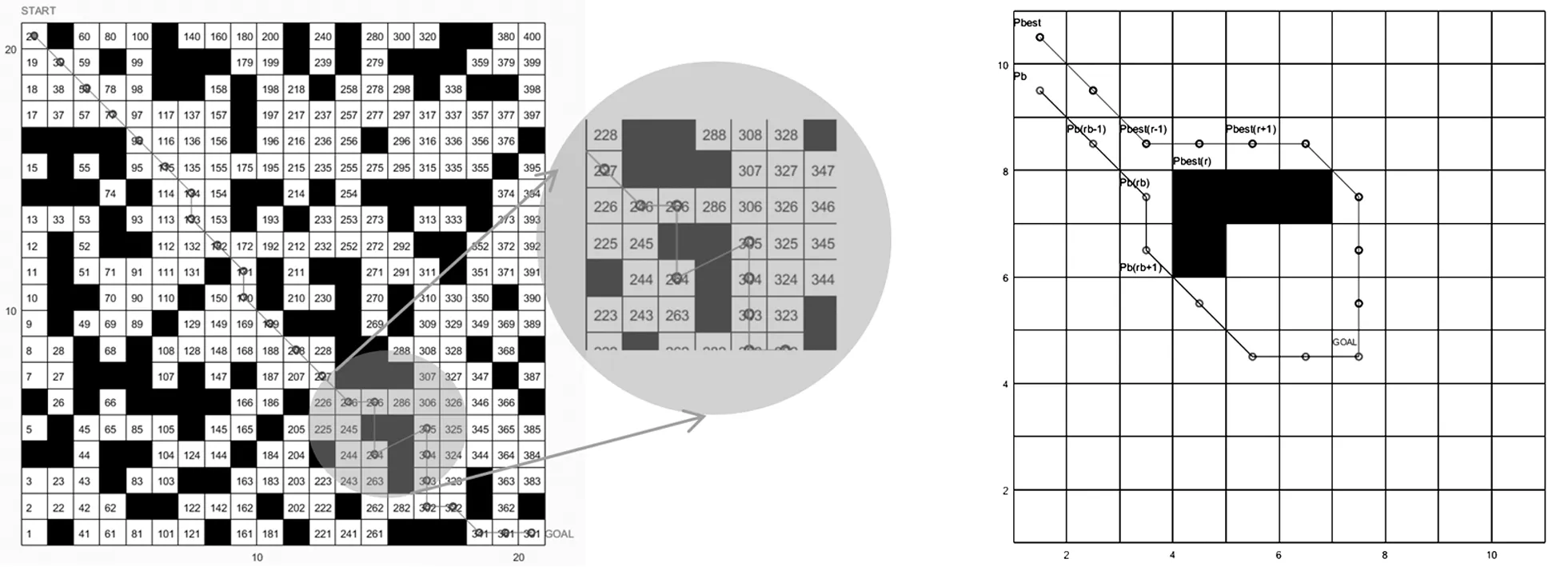
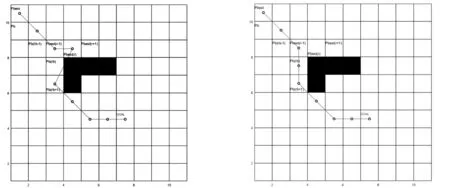
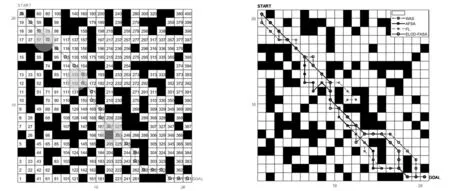
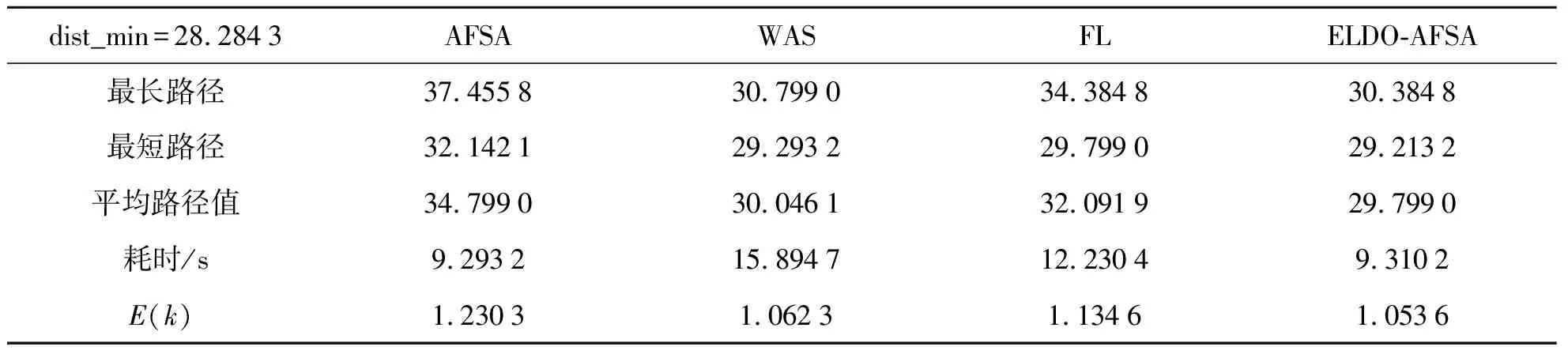
式中,pnest为人工鱼下一时刻的位置;prand为在pi可行域中随机选取一个栅格作为下一时刻位置.若可行域中找到下一位置pk,食物浓度Hk,满足Hk (2) 定义7:鱼群追尾行为,设pi为当前人工鱼位置,其附近伙伴的中食物浓度最低的人工鱼群位置为plow,物浓度为Hlow.追尾行为可描述为: (3) 传统人工鱼群算法通过循环不断地执行群聚和追尾行为,不断将每一时刻中的最优解更新到公告板上,最终最优解附近会聚集较多的人工鱼,然后得出最优解. 这种寻优方式在应用到栅格环境的机器人路径规划问题上,会出现严重的次优解干扰路径规划的合理性问题.基于鱼群算法的移动机器人路径规划如图1所示. 针对此问题做如下证明.最优解和次优解路径曲线如图2所示.设: (1)1~k时刻,全局最优解为pbest,其食物浓度为Hbest,该处鱼群编号为r. (2)pb为次优解,其食物浓度为Hb,该处鱼群编号记为rb. (3)pbest(r)和pb(rb)表示编号为r和rb的人工鱼群行走的路径. 如图2所示,上方pbest路径为鱼群r的路径曲线,下方pb曲线为鱼群rb的路径曲线.在鱼群到达pbest(r)和pb(rb)位置之前,编号为r的鱼群和编号为rb的鱼群到目标点的欧氏距离为: (dr)2=‖pbest(r)-GOAL‖2=(xr-xg)2+(yr-yg)2, (4) (drb)2=‖pb(rb)-GOAL‖2=(xrb-xg)2+(yrb-yg)2, (5) 式中,Pbest(r)=pbest(xr,yr)为编号r鱼群的位置;pb(rb)=pb(xrb,yrb)为编号rb鱼群的位置.由图2可知,总有xr (6) 因为xr 图1 基于鱼群算法的移动机器人路径规划 图2 最优解和次优解路径曲线 同理可证,从k+1时刻到最终到达目标点,pb(rb)之后的点会存放到road集合中,即road={…,pbest(r-3),pbest(r-2),pbest(r-1),pb(rb+1),pb(rb+2),pb(rb+3),…}. 特别地,在k时刻,因为pbest(r-1)的下一个离目标点距离最小的点在障碍物区间内,所以导致pbest(r)和pb(rb)同时为最优解,因为存在随机性,所以pbest(r)和pb(rb)都有50%概率被存到road集合中.所以, (Ⅰ)当pbest(r)被存到road中后,road1={…,pbest(r-3),pbest(r-2),pbest(r-1),pbest(r),pb(rb+1),pb(rb+2),pb(rb+3),…}. (Ⅱ)当pb(rb)被存到road中后,road2={…,pbest(r-3),pbest(r-2),pbest(r-1),pb(rb+1),pb(rb+2),pb(rb+3)…}. 为了解决鱼群算法的次优解干扰全局路径规划的问题.设计了基于经验学习的鱼群算法.经验学习方法在于学习规划失败的经验.算法一直跟踪最优解鱼群的位置,若该鱼群k时刻的位置不再是全局最优,那么就将时刻从k~k-2的路径值从road集合中删除,同时在栅格地图上赋予权值w∈[1,1.5),权值w从k~k-2时刻走过的栅格依次递减,同时重新设计食物浓度函数为: 图3 road1路径曲线 图4 road2路径曲线 鱼群经验学习算法主体部分步骤如下: Step 1:当前k时刻最优解的鱼群编号是否与上一时刻相同,若是,则继续跟踪最优解鱼群,执行Step 1;若否,则转Step 2; Step 2:将路径集合中k~k-2的位置去除,所有鱼群清除k~k-2时刻的位置数据,同时在栅格地图上对应最优解鱼群走过的栅格,赋予权值w,转Step 3; Step 3:更新实物浓度函数,转Step 4; Step 4:鱼群从k-2时刻以新的实物浓度函数重新开始鱼群基本行为跟踪最优解鱼群的编号,转Step 1. 为了验证基于经验法的鱼群算法对于解决鱼群算法次优解干扰全局路径规划合理性问题的可行性,证明如下.鱼群经验学习后赋予权值如图5所示,设编号为r的鱼群在学习了图3中的错误经验之后,对pbest(r-1),pbest(r),pbest(r+1)位置区域,赋予权值w1,w2,w3;同时在road集合中删除这些路径位置. 于是鱼群从k-2时刻重新开始.已知w3=1,w2 因为w3=1,所以当鱼群再次到达此位置时,其可行域中下一时刻的候选位置为pbest(r)和pb(rb),记到目标点的欧式距离分别为: (7) (8) (9) 由图5可知,总有w2∈(1,1.5),xrb>xr,yrb>yr,|xg-xrb|=|yg-yr|,|xg-xr|=|yg-yrb|,则 (10) 同理可证,pb(rb+1)以后的位置也都被记录到road集合中,即road={…,pbest(r-1),pb(rb),pb(rb+1),pb(rb+2),…}. 由此可见,通过经验学习后的鱼群不会再因障碍物区域的阻拦,而出现次优解干扰全局路径规划合理性的问题.基于经验学习的鱼群算法的路径规划如图6所示.栅格环境为20*20,障碍物栅格占全部栅格的35%. 基于经验学习的鱼群算法,在学习了图1中错误的经验后,给了图6所示的合理的全局路径规划结果,使得鱼群成功地避开了{211,210,230,270,269}等栅格号的陷阱诱惑,解决了鱼群算法次优解干扰全局路径规划合理性问题. 如图6中的路径曲线,在3个圆形区域的路径,并不是最优的路径,出现了路径冗长的问题.为了解决路径规划中出现的路径冗长问题,研究提出优化检测算法. 在前期鱼群距离目标点距离较远,产生的最优解缺乏目标位置的影响,存在路径冗长的问题,如图6中3块圆形区域所示,R(t)在前期的取值会适当的大,使得鱼群移动方向能够受到目标点的影响,而不是仅仅参考当前鱼群最优解;随着鱼群不断接近目标点,R(t)的取值逐渐减小.由此可见,需要被优化检测的解t越小,说明路径处于前期或者中期,R(t)的值较大;而当t越大,说明路径进入后期,R(t)的值变小. 不妨假设,划分路径前75%为鱼群寻优的前期和中期,后25%为鱼群寻优后期.给出优化检测算子R(t)的表达式如下: (11) 式中,p(kx,ky)为k时刻解的最优鱼群的位置坐标;goal(x,y)为目标位置的坐标;D(k)表示p(kx,ky)到goal(x,y)的整数倍距离. (12) (13) 式中,ki为已被优化检测的解的个数. 在图6中,设第一个圆的圆心所在位置为k时刻全局最优解,上一个点的位置记为k-1时刻的全局最优解,下一点的位置记为k+1时刻的全局最优解,以此类推,分别为…,k-1,k,k+1,…时刻最优解的位置.优化检测算法满足以下条件: (1)在优化检测第一个圆后,k+1,k+2,k+3路径位置被优化后,不会再加入到待优化检测的序列; (2)下一时刻直接从k+4时刻的路径位置开始优化检测. 图5 鱼群经验学习后赋予权值 图6 基于经验学习的鱼群算法的路径规划 将研究算法与蚁群算法和模糊逻辑算法进行仿真实验,并对数据进行比较.在对比实验中,以下参数始终不变:N=50,visual=10,δ=0.618,Nant=50栅格中障碍物区域占整个栅格数的35%.其中,N为鱼群数,visual为鱼群的视野,δ为拥挤度,Nant为蚂蚁的个数. 20*20栅格环境下WAS,AFSA,FL和ELDO-AFSA算法仿真得出的路径规划结果如图8所示.从仿真结果不难看出研究提出的ELDO-AFSA算法在路径规划上表现效果优于其他3种算法.在20*20,40*40,60*60栅格环境下的AFSA,WAS,FL和ELDO-AFSA算法的路径长度、算法耗时和评价函数值分别如表1、表2、表3所示.通过对比可以看出,研究提出的ELDO-AFSA算法全程路径短,而且随着环境的复杂化,算法的评价函数值波动小,算法稳定性能优于WAS,AFSA和FL3种算法. 图7 基于检测算子优化算法后的路径规划 图8 20*20栅格移动机器人路径规划 dist_min=28.2843AFSAWASFLELDO-AFSA最长路径37.455830.799034.384830.3848最短路径32.142129.293229.799029.2132平均路径值34.799030.046132.091929.7990耗时/s9.293215.894712.23049.3102E(k)1.23031.06231.13461.0536 表2 40*40栅格环境算法比较 表3 60*60栅格环境算法比较 针对鱼群算法在解决移动机器人路径规划中出现的次优解干扰路径合理性问题,设计了具有检测算子的经验学习鱼群算法(ELDO-AFSA),使每条鱼都具有学习错误经验的能力,在解决次优解干扰路径规划合理性问题上效果显著.同时针对路径冗长的情况,引入了优化检测算子,在不改变路径合理性的前提下,使路径不断接近全局最优路径.最后将ELDO-AFSA算法与AFSA,WAS,FL算法进行比较,对比仿真实验体现了ELDO-AFSA算法具有更强的收敛性、稳定性和可靠性.但是,对于栅格环境庞大且地图中的“陷阱”区域较多时,鱼群会耗费较多的时间在学习经验上.因此,接下来的工作方向会更加注重提高鱼群在大量“陷阱”区域环境下的学习效率问题,使得算法的收敛速度更快.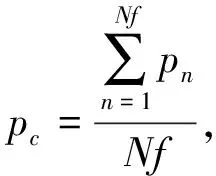
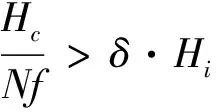
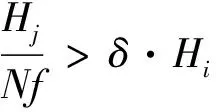
2 经验学习鱼群算法及收敛性分析

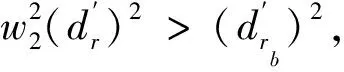
3 具有检测算子的经验学习鱼群算法
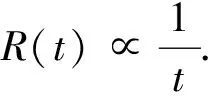

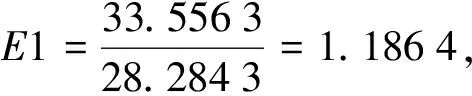

4 算法仿真比较实验


5 结论
