里德里原子偶极阻塞效应的平均场的研究
2019-03-19毛如圣刘子龙
毛如圣, 张 波, 刘子龙, 杨 波
(武汉理工大学理学院物理系, 武汉 430070)
1 引 言
里德堡原子是指原子最外层电子被激发到主量子数n很大的高激发态原子[1],它具有自发辐射寿命长、极化率大和电偶极矩强等特殊的物理性质[2]. 里德堡原子对外部电磁场十分敏感,不仅可以利用其对外场进行探测,还可以利用外场实现对里德堡原子的操控[3~6]. 随着激光冷却技术的发展,超冷里德堡原子的获得使多普勒效应得到有效的抑制,推进了里德堡原子间相互作用的研究与应用[7]. 里德堡原子之间的相互作用大致可分为两类[8]:一类为长程范德瓦尔斯相互作用,其相互作用能为Vint=-C6/R6;另一类称为偶极-偶极相互作用,其相互作用能为Vint∝1/R3,且这种相互作用比范德瓦尔斯相互作用更强. 里德堡原子之间的相互作用导致里德堡能级频移,从而在里德堡原子周围一定距离内的其他原子无法被激发到里德堡态,这个现象被称为偶极阻塞效应[9,10],这个距离为偶极阻塞半径[11]. 利用里德堡原子的相互作用与偶极阻塞效应可以实现量子比特、量子逻辑门以及量子纠缠态的制备[12~16],这是量子信息处理[17]的基础量子计算[18]的关键. 约化密度矩阵法[19]和量子蒙特卡罗[20, 21]等方法已被用于计算和模拟里德堡原子间的相互作用和偶极阻塞效应. 本文利用平均场法[22]计算里德堡原子的偶极阻塞效应,在主量子数和原子密度不大的条件下[23],计算过程较前述两种方法简单,里德堡原子间的相互作用的影响可以得到简化,同时本文还分析了主量子数、拉比频率与原子密度对偶极阻塞效应的影响.
2 平均场模型
对于一个存在相互作用的多原子系统,其每一个原子都将受到周围原子的影响. 将其周围原子的相互作用进行迭加,并根据原子密度分布进行平均,从而可以形成一个只依赖于此原子的平均势场,这个平均势场可用一个单体算符来描述. 即利用平均场法,可以将单个原子受到相互作用力用一个算符来表达.

(1)
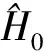

(2)
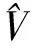
(3)
其中ri与rj分别表示第i和j个原子的位矢,C6为里德堡原子间的相互作用系数[26],利用朗道平均场理论,忽略场的二阶涨落,即(|e〉i〈e|-ρee)(|e〉j〈e|-ρee)≈0,这里ρee为原子处于里德堡态的几率,可以得到:
|e〉i〈e||e〉j〈e|≈|e〉i〈e|ρee+
(4)
其中第二步将第i和j个原子当做等价的来处理.
当原子数较多时,可以将原子看作是准连续的,于是求和符号化为积分[27]. 当两原子之间的距离r=ri-rj远小于偶极阻塞半径Rd即r<
(5)
再将(4)和(5)式代入到(3)式中,在忽略不影响密度矩阵运动方程的常数项后,可以求得相互作用哈密顿量的表达式:
(6)
3 速率方程
由主量子方程:
(7)
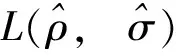
(8)
(9)
(10)
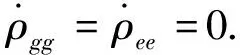
(11)
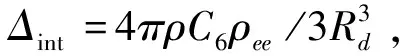
4 结果与分析讨论
4.1 偶极阻塞效应对原子跃迁的影响
取铷原子团的密度为ρ=3×1010cm-3,激光场拉比频率为Ω=5 MHz、自发辐射概率为Γ=6 MHz、激光线宽为γ=2 MHz,我们计算了不同频率失谐量下,铷原子团被激发到n=50的里德堡态的几率,如图1所示. 图中黑色实线是不考虑原子间偶极相互作用(即公式(9)中Δint=0)时,原子的激发几率;红色虚线是考虑原子间偶极相互作用(Δint≠0)时,原子的激发几率.
如果不断减小铷原子团的密度,原子间偶极相互作用会随之不断减小,以至图中两条曲线重合. 在不考虑原子间偶极相互作用且激光频率失谐量Δ=0时,得到最大的激发几率,此时被激发到里德堡态的原子占比约为22.73%(见图1中黑色实线). 在ρ=3×1010cm-3时,原子间偶极相互作用不为0(Δint≠0)不可忽略,红色虚线是加上原子间偶极相互作用后,里德堡原子的占比. 原子间偶极相互作用使里德堡能级发生频移,此时只有当激光频率失谐量Δ与里德堡能级频移Δint之和为0时,才能得到最大激发几率,仅为19.32%(见图1中红色虚线)这是因为偶极阻塞效应导致处于阻塞半径内的原子无法被激发到里德堡态.
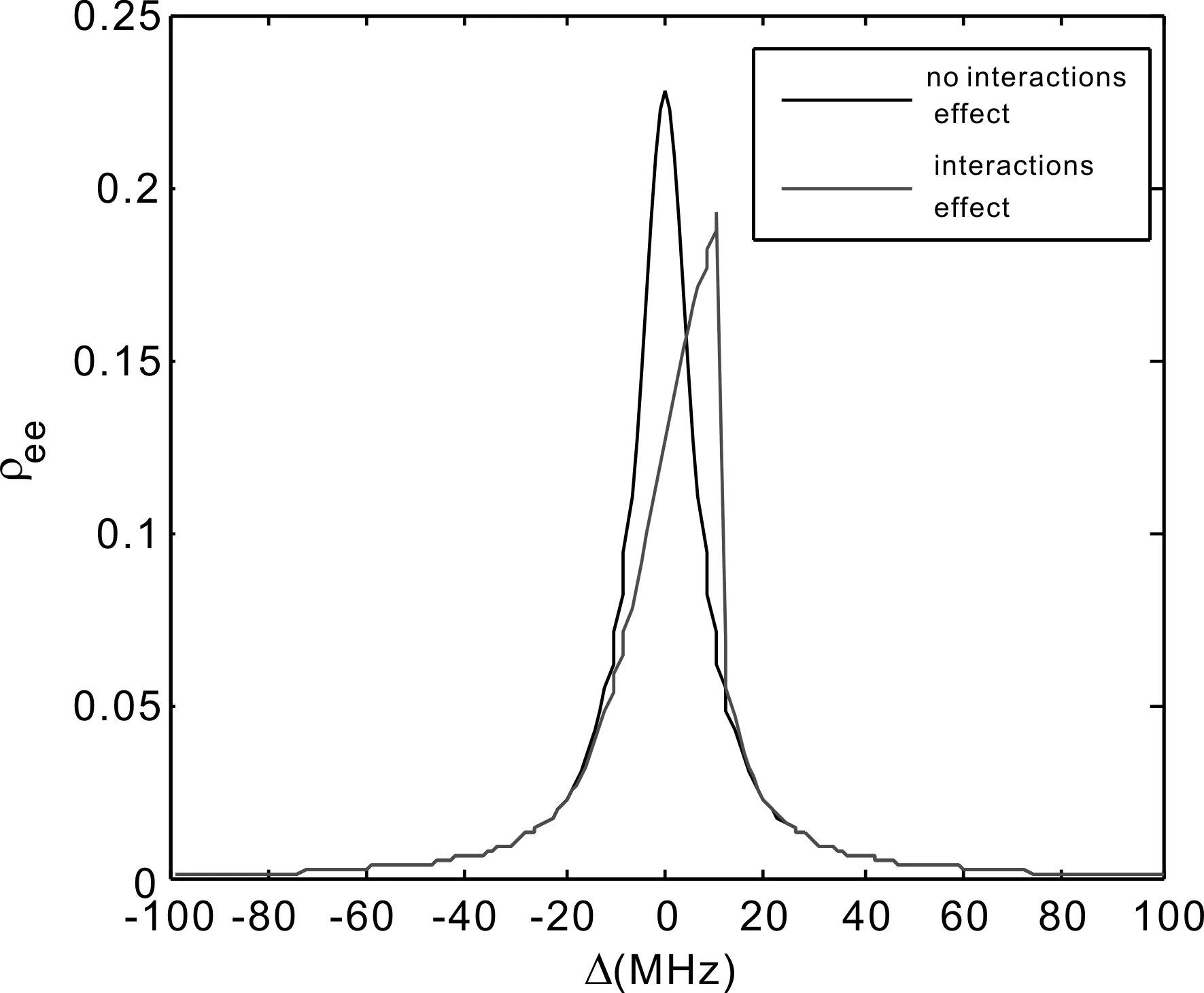
图1 里德堡原子占比Fig.1 Population of excited Rydberg atoms vs laser detuning
4.2 主量子数对偶极阻塞效应的影响
被激发到不同主量子数的里德堡原子之间的相互作用大小不同,所导致的偶极阻塞效应也不同. 对于密度为ρ=3×1010cm-3的铷原子团,拉比频率为Ω=5 MHz、自发辐射概率为Γ=6 MHz、激光线宽为γ=2 MHz,且满足Δ+Δint=0时,我们计算了主量子数n从50到80时,里德堡原子的激发几率,如图2所示. 这里所选取原子团的密度较小,原子间的相互作用相对较弱,在n=80时,仍可用平均场法来近似计算.
随着主量子数的增大,里德堡原子的跃迁偶极矩急剧增大,里德堡原子间的相互作用力也随之增大,导致里德堡能级频移增大,偶极阻塞效应强烈,抑制基态原子向里德堡态的跃迁. 从而在图2的曲线可以看出,主量子数的越大,被激发到里德堡态的原子数目越少. 当主量子数n=50时,被激发到里德堡态的原子占比约为19.32%,而当主量子数n=80时,被激发到里德堡态的原子仅占了2.44%. 即随着主量子数的增大,里德堡原子的偶极阻塞效应越明显.
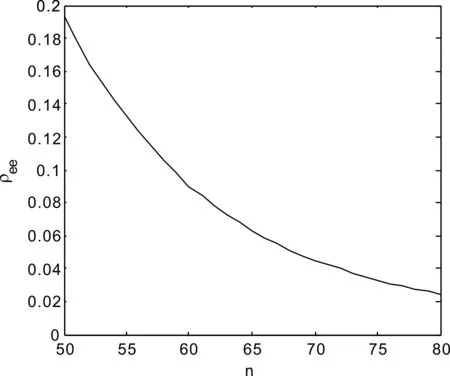
图2 不同主量子数时里德堡原子的激发几率Fig.2 population of excited Rydberg atoms at different principal quantumnumbers
4.3 拉比频率对偶极阻塞效应的影响
激光功率将会影响里德堡原子的偶极阻塞效应,而激光功率越大对应的拉比频率也就越大. 对于密度为ρ=3×1010cm-3的铷原子团,其自发辐射概率为Γ=6 MHz、激光线宽为γ=2 MHz,满足Δ+Δint=0时,我们计算了拉比频率Ω从0 MHz到20 MHz时,被激发到n=50的里德堡态原子占比,如图3所示.
当拉比频率小于5 MHz ,随着拉比频率的增加,被激发到里德堡态的原子数目线性增大,这是因为拉比频率较小时,被激发到里德堡态的原子数很少,处于偶极阻塞半径内的原子也较少,大部分原子的里德堡能级不会有显著变化,不会出现偶极阻塞效应;当拉比频率大于5 MHz,随着拉比频率的增大,里德堡原子数目逐渐增加,处于偶极阻塞半径内的原子增多,大部分原子的里德堡能级也都发生明显频移,导致偶极阻塞效应增强;当拉比频率足够大(约大于15 MHz)时,被激发到里德堡的原子数目达到饱和,大部分原子都处于偶极阻塞半径内,原子无法被激发到里德堡态,从而有十分明显的偶极阻塞效应.
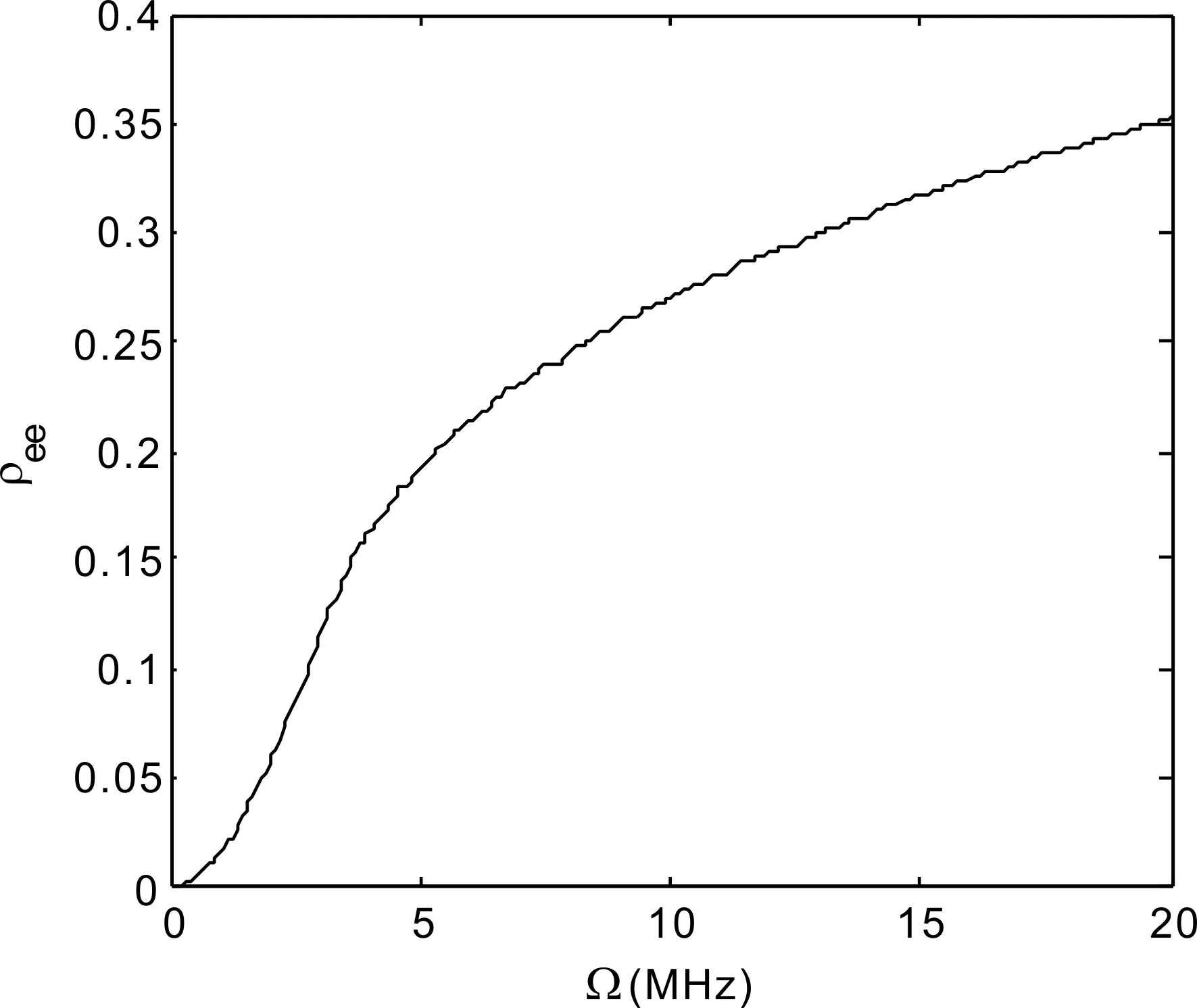
图3 不同拉比频率时的里德堡原子的激发几率Fig. 3 population of excited Rydberg atoms at different Rabi frequencies
4.4 原子密度对偶极阻塞效应的影响
同样原子密度也将影响偶极阻塞效应,原子的密度越大则原子间的间距越小. 当拉比频率为Ω=5 MHz、自发辐射概率为Γ=6 MHz、激光线宽为γ=2 MHz,满足共振条件Δ+Δint=0时,我们计算了原子间距a从10-7m逐渐增大到的10-5m时(对应密度从1015cm-3变化到109cm-3),被激发到n=50的里德堡态原子占比,如图4所示. 主量子数为n=50,在所取密度范围内(109cm-3~1015cm-3),原子间的相互作用较弱,仍可以用平均场法来近似.
当原子的间距a远小于偶极阻塞半径Rd时,原子将会受到强大偶极相互作用,所有的基态原子均无法被激发到里德堡态,偶极阻塞效应明显;当原子团密度降低时,原子间距a也逐渐增大,原子间的偶极相互作用随之降低,部分原子处于偶极阻塞半径之外,从而这些基态原子能够被激发到里德堡态,处于里德堡态的原子数目也逐渐增加,偶极阻塞效应减弱;当原子间距a足够大时,原子之间的偶极相互作用力非常弱,此时里德堡原子占比为一定值,偶极相互作用可忽略.
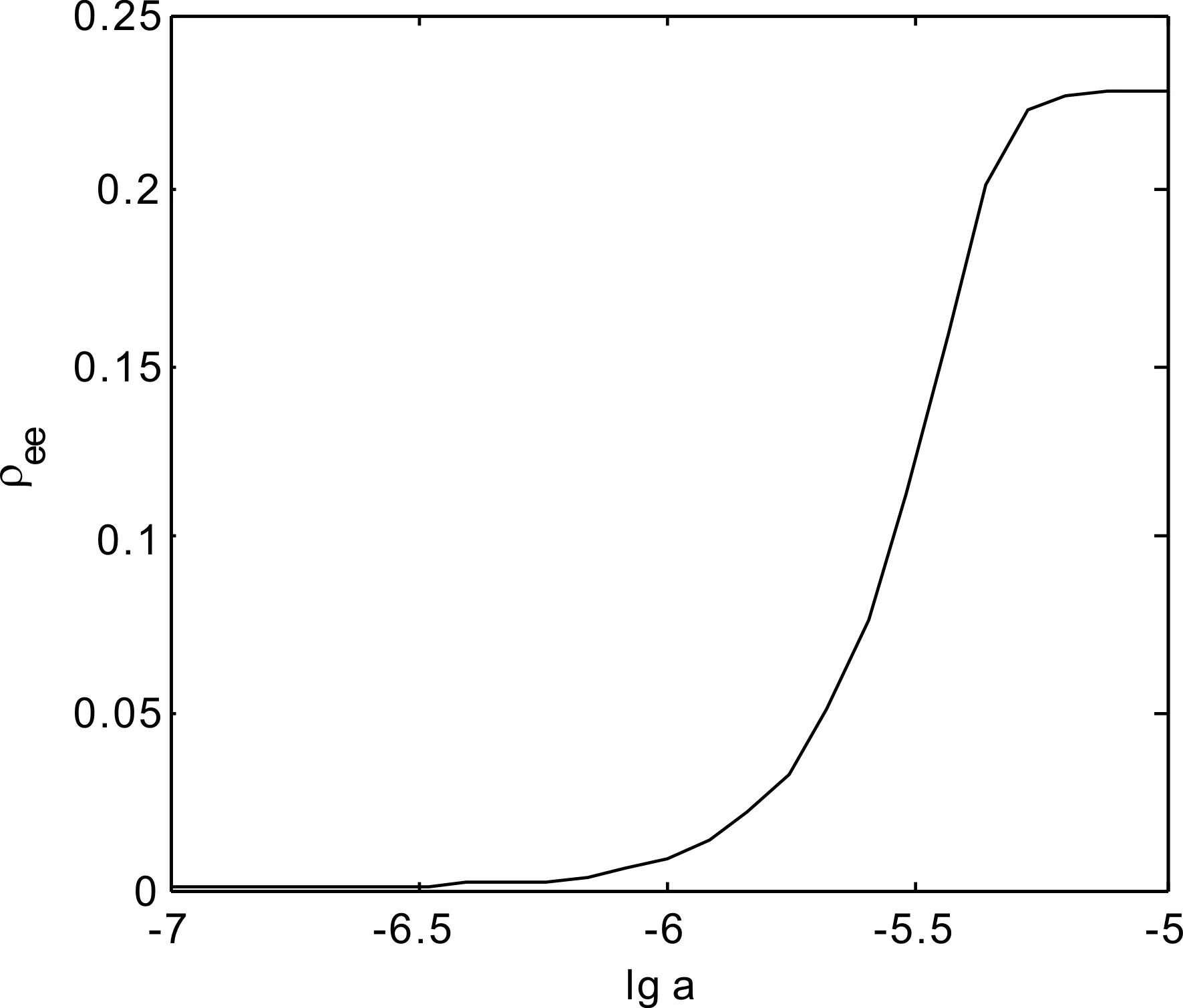
图4 不同原子间距时的里德堡原子的激发几率Fig. 4 population of excited Rydberg atoms vs atomic distance
5 结 论
本文利用平均场法计算了给定铷原子团在不同条件下的里德堡态激发几率,分析了不同主量子数、拉比频率以及原子密度时里德堡原子的偶极阻塞效应. 原子间的偶极相互作用使里德堡能级频移,出现偶极阻塞效应,从而降低基态原子激发到里德堡态的几率. 主量子数越大,原子间的偶极相互作用越强,导致能级频移越大,偶极阻塞效应越明显. 激光功率增强,拉比频率的增大,使得里德堡态的原子数目增加,但这也将导致偶极相互作用的增大,当里德堡原子达到一定数目时,即使再增加拉比频率,由于偶极阻塞效应里德堡态原子占比达到饱和. 原子密度越大,原子间距越小,原子间的偶极相互作用越强,偶极阻塞效应越明显. 相反,原子密度越小,原子间距越大,原子间的偶极相互作用越弱.
本文中我们假定所有原子之间的距离是相等的,适用于光晶格中的原子分布,而实验中捕获在磁光阱中的原子团是高斯分布,后续我们将在计算中考虑这种非等距分布原子团中的原子的相互作用,并分析其偶极阻塞效应. 偶极阻塞效应的研究有助于量子比特与量子逻辑装置的实现,促进量子信息与多体物理等领域的发展.
