BeF+离子电子态的光谱常数研究

张如旭， 孙金峰

(河南师范大学 物理与材料科学学院，新乡 453007)

1 引 言

氟化物作为重要的化学物质，被广泛的应用于化学领域. 与其他元素结合，合成物具有耐热耐腐蚀的特性，被广泛用于电器，办公自动化设备，汽车等领域. 关于BeF分子的电子结构和光谱常数的计算有很多，1967年，Novikov等人做了相关实验，研究了BeF的散射光谱[1, 2]. 而对于BeF+离子的研究却很少. 在1986年，Harry 等[3]首次计算了关于BeF分子和BeF+离子的低价相关电子态，得到了一系列的光谱常数和和分子常数等. 1992年，Ornallas[4]通过计算BeF和BeF+的相关电子态数据，对比研究了BeF+的基态与激发态特性. 2010年，陈恒杰等人[5]计算了BeFх的解析势能函数和光谱常数，分别给出了BeF分子和BeF+，BeF-离子基态X1Σ+的光谱常数.

为了提供更多数据，为以后的实验和理论计算提供更全面的参考，本文计算了BeF+离子第一离解极限的四个低态的光谱常数和分子常数，同时还计算了第二离解极限的十二个激发态的光谱常数和分子常数. 已知的理论计算中[3, 4]，只给出了BeF+离子第一离解极限三个束缚态X1Σ+，a3Π 和A1Π 的光谱常数.

利用高维相对论多参考配置与戴维森修正(MRCI + Q)相互作用，对BeF+离子的基态以及激发态进行了理论计算. 获得了BeF+离子前两个离解极限的十六个Λ-S态的势能曲线. 将这些势能曲线进行拟合，获得其中十五个束缚态的光谱常数和分子常数，13Σ+为排斥态，没有相关数据，不做研究.

包括基态激发能量Te，平衡核间距Re，谐振频率ωe，一阶和二阶非简谐常数ωexe和ωeye，振动耦合常数αe，旋转常数Be和解离能De等的光谱常数和分子常数，是分析光谱性质的重要参数.为了精确的计算这些光谱参数， 我们用Numerov的方法求解振动薛定谔方程[6]. 这种方法首先通过求解振动薛定谔方程从解析势直接向前确定振动常数，然后通过拟合前十个振动级来评估光谱参数.

2 计算方法

用从头计算方法在MOLPRO程序包中进行计算[7]. 光谱常数借助于LEVEL程序来确定[8]. 双原子团BeF+离子属于对称点群C∞ν. 但是由于MOLPRO程序的局限性，所有的计算都是在C2ν点组中进行的. C2ν点群有四个不可约表示，A1，A2，B1和B2.对应于C∞ν→C2v的对称运算分别为Σ+→A1，Σ-→A2，Π→B1+ B2和Δ→A1+ A2.利用态平均完全活性空间自洽场(SA-CASSCF)方法研究BeF+的基态和低激发态[9, 10]，在计算中同时运用了内收缩多参考相互作用方法和戴维森校正(MRCI + Q)[11, 12]. 在CASSCF计算中，有效空间由八个分子轨道(MO)组成，即由四个a1，两个b1和两个b2对称的MO轨道组成. 当我们把八个最外面的分子轨道(MOs)4a1，2b1和2b2放入到当前计算的活性空间中时，可以首先适当地计算得到势能曲线(PECs). 但是由于BeF+离子几个态的势能曲线在随着核间距的增加，出现了较为陡峭的趋势. 为了使PECs平滑，我们在活动空间中包含两个额外的轨道MO(一个b1和一个b2). 进而使所有的势能曲线在有效核间范围内都是平滑的，并且每个PEC都是收敛的. 也就是说，在前面的CASSCF和后面的icMRCI计算中，将十二个最外层的MO(6a1，3b1和3b2)放入活性空间中. F原子的2s2p轨道中BeF+离子的2s2p轨道和9价电子的三个价电子被置于活性空间中，由活性空间组成. 换句话说，在计算中，BeF+阳离子中的九个价电子分布为十个最外层价电子轨道(3-6σ，1π，2π和3π). 最外层价轨道的能量排序为3σ4σ1π5σ2π6σ3π. 所以，这个活动空间可以被表示为CAS(9，10). 4个内层电子被放入2个闭壳层轨道(2a1)，这对应了BeF+阳离子中的1σ和2σ MOs. 在计算中，外部轨道的数量为118，包括对称MOs，50a1，28b1，28b2和12a2. 总之，使用12个轨道(6a1，3b1和3b2)来计算所有Λ-S状态的PEC. 经过这些MOs的调整后，所有的PECs在目前的核间距范围内都是平滑的，而且每个PEC都是收敛的. 为了准确地确定16个Λ-S态的势能曲线(PECs)，这里使用的点间距为每个状态0.02 nm，而在平衡核间位置附近我们选择了点间距为0.002 nm. 在每个态的平衡核间距位置附近采用较小的点间距，可以更清楚地显示每个PEC的特性.

为了提高光谱参数的质量，我们在势能曲线计算中考虑了核价相关修正和标量相对论修正. 在这项工作中，核价相互修正被考虑在cc-pCVTZ基组[13]中，其贡献被表示为CV. 需要指出的是，核价相关修正计算是在icMRCI + Q理论层面计算的，并且被应用在每个态的势能曲线上. 在cc-pVTZ基组[14]的基础上，通过三阶Douglas-Kroll哈密顿量近似(DKH3)考虑标量相对论修正，并将其考虑在每个态的势能曲线上. 标量相对论修正的贡献表示为DK.

3 结果与讨论

用文献[15]中的方法，在icMRCI+Q/Q5+CV+DK条件计算得到了BeF+离子16个态的势能曲线. 为便于比较不同态的势能曲线的性质，我们把BeF+离子的16个态的势能曲线都描绘在一起，如图1. 为了使所有的态收敛，我们选择核间距R = 0.28 - 0.9 nm的计算长度. 其中在平衡核间距附近R = 0.082 - 0.28 nm选择步长为0.002 nm，而在核间距R = 0.28 - 0.9 nm范围内选择步长为0.02 nm. 在所计算的十六个态中，有十五个束缚态和一个排斥态. 通过求解相应的核薛定谔方程，得到了这十五个束缚态的光谱常数. 相关的光谱常数列于表1.

3.1 X1Σ+, a3Π, A1Π 和13Σ+态

本文计算的十五个束缚态没有发现实验参考文献，因此没有相关的实验数据. 在关于BeF+离子的几篇理论计算文章中，给了三个态X1Σ+, a3Π 和A1Π的光谱常数和分子常数. 其中，关于基态X1Σ+在文献[3-5]均给出了相关的光谱常数，而激发态a3Π 和A1Π 只在文献[3, 4]中有相关光谱常数数据. 其余的十二个激发态均没有相关光谱常数给出. 从图1能看出，基态X1Σ+具有很深的单势阱，势阱深度是49038.49 cm-1. 由表1可以看出，本文所计算的X1Σ+态的平衡核间距与其他三组数据非常接近. X1Σ+态具有明显的单一组态特征，并且主要价电子组态为3σ24σ21π45σ02π06σ03π0(0.8511). 在文献[3]中也给出了单电子组态，但没有给出相应的权重.

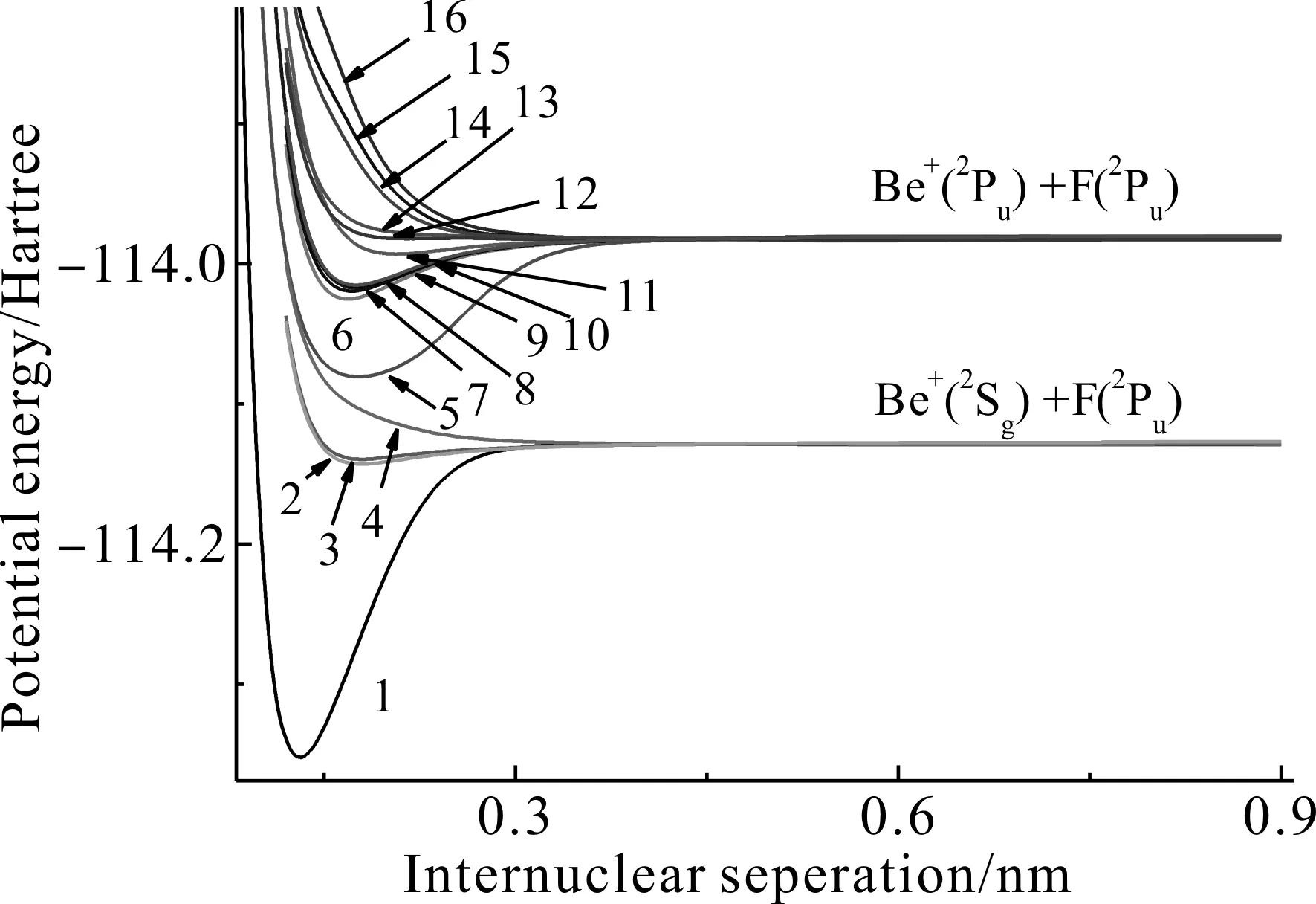
图1 BeF+离子的16 Λ-S态的势能曲线1, X1Σ+; 2, a3Π; 3, A1Π; 4, 13Σ+; 5, 21Σ+; 6, 23Σ+; 7, 13Δ; 8-11Δ, 9, 11Σ-; 10, 13Σ-; 11, 31Σ+; 12, 21Π; 13, 33Σ+; 14, 33Π; 15, 31Π; 16, 23Π. Fig. 1 PECs of 16 Λ-S states of BeF+ cation. 1, X1Σ+; 2, a3Π; 3, A1Π; 4, 13Σ+; 5, 21Σ+; 6, 23Σ+; 7, 13Δ; 8-11Δ, 9, 11Σ-; 10, 13Σ-; 11, 31Σ+; 12, 21Π; 13, 33Σ+; 14, 33Π; 15, 31Π; 16, 23Π.

文献[3, 4]计算了激发态a3Π和A1Π，态a3Π 为浅单势阱，势阱深度是3573.035 cm. a3Π态拥有35振动状态，其中的振动能级分别是192.46，552.10，881.86，1184.06，1460.32，1711.14，1937.58，2140.99，2322.07，2482.26，2745.71，2851.44，2943.16，3023.04，3092.14，3275.71，3305.71，3305.71，3354.67，3369.27，3386.29，3406.04，3471.01，3449.18，3471.01，3491.13，3506.13，3506.13，3506.13，3552.19，3569.53 cm-1其中 ν = 0-34. 比较稳定，容易观察到. a3Π 态的离解能为0.4430 eV，a3Π态的平衡核间距位置与基态平衡核间距位置相差0.04826 nm. 而a3Π 态具有明显的单一组态特征，其主要的价电子组态为3σ24σ21π35σ12π06σ03π0(0.9356). 可以看出a3Π 和 X1Σ+态之间的主要电子跃迁为5σ→1π.

A1Π态的阱深为2819.713 cm-1. 相对于a3Π来说拥有更浅的势阱，A1Π 态具有32个振动状态，振动能级分别是 184.75, 523.06, 822.57, 1083.91, 1308.97, 1501.65, 1665.55, 1807.10, 1928.03, 2034.10, 2127.27, 2209.31, 2280.80, 2343.31, 2399.32, 2447.91, 2489.88, 2527.62, 2561.89, 2591.25, 2614.28, 2630.62, 2646.28, 2665.64, 2686.15, 2707.52, 2728.92, 2749.27, 2765.75, 2779.08, 2798.60, 2808.81 cm-1. A1Π 态具有明显的单一组态特征，其主要的价电子组态为3σ24σ21π35σ12π06σ03π0(0.9428). 同样的，A1Π 态和 X1Σ+态之间的主要电子跃迁为5σ→1π. 两个激发态a3Π和A1Π的振动能级相似，都很容易在实验过程中观察到. 而第一离解极限中的另一个态13Σ+没有势阱，作为排斥态，计算过程中并没有相应的拟合数据.

3.2 21Σ+, 23Σ+, 13Δ, 11Δ, 11Σ-, 13Σ-, 31Σ+, 21Π, 33Σ+, 33Π, 31Π 和23Π态

第二离解极限的十二个态21Σ+, 23Σ+, 13Δ, 11Δ, 11Σ-, 13Σ-, 31Σ+, 21Π, 33Σ+, 33Π, 31Π 和23Π 均是束缚态，并且没有发现相关的参考文献有相关的计算研究. 对于八个单势阱态13Δ, 11Δ, 11Σ-, 13Σ-, 31Σ+, 33Σ+, 33Π 和31Π态，其中13Δ, 11Δ, 11Σ-和13Σ-拥有较深的势阱，13Δ态有39个振动态，振动能级293.74，866.63，1419.19，1951.90，2463.99，2955.93，3427.28，3877.64，4307.20，4715.45，5102.23，5466.69，5809.07，6128.70，6424.81，6697.61，6945.60，7170.21，7370.76，7547.18，7700.32，7832.02，7944.09，8038.04，8116.16，8183.24，8240.27，8281.23，8312.75，8347.35，8376.60，8399.49，8428.06，8460.47，8493.46，8522.30，8530.18，8539.61，8550.93 cm-1.

11Δ态有39个振动态，振动能级280.29，825.68，1351.79，1858.21，2345.43，2812.73，3261.19，3688.82，4096.02，4483.29，4848.81，5193.25，5515.08，5814.72，6091.76，6346.13，6576.25，6782.68，6964.99，7124.15，7264.38，7385.03，7483.36，7567.25，7636.59，7695.43，7745.60，7788.19，7823.58，7855.71，7885.03，7909.74，7940.43，7974.60，8009.09，8039.92，8050.39，8063.28，8073.59 cm-1.

11Σ-态有35个振动态，振动能级276.24，816.50，1337.22，1837.97，2318.41，2779.97，3220.85，3641.38，4041.07，4419.36，4776.52，5111.46，5424.32，5714.07，5978.26，6218.80，6437.84，6632.63，6802.84，6949.82，7074.39，7180.58，7270.72，7344.93，7409.92，7464.42，7506.90，7541.89，7571.25，7599.99，7623.36，7652.00，7684.64，7717.39，7745.65 cm-1.

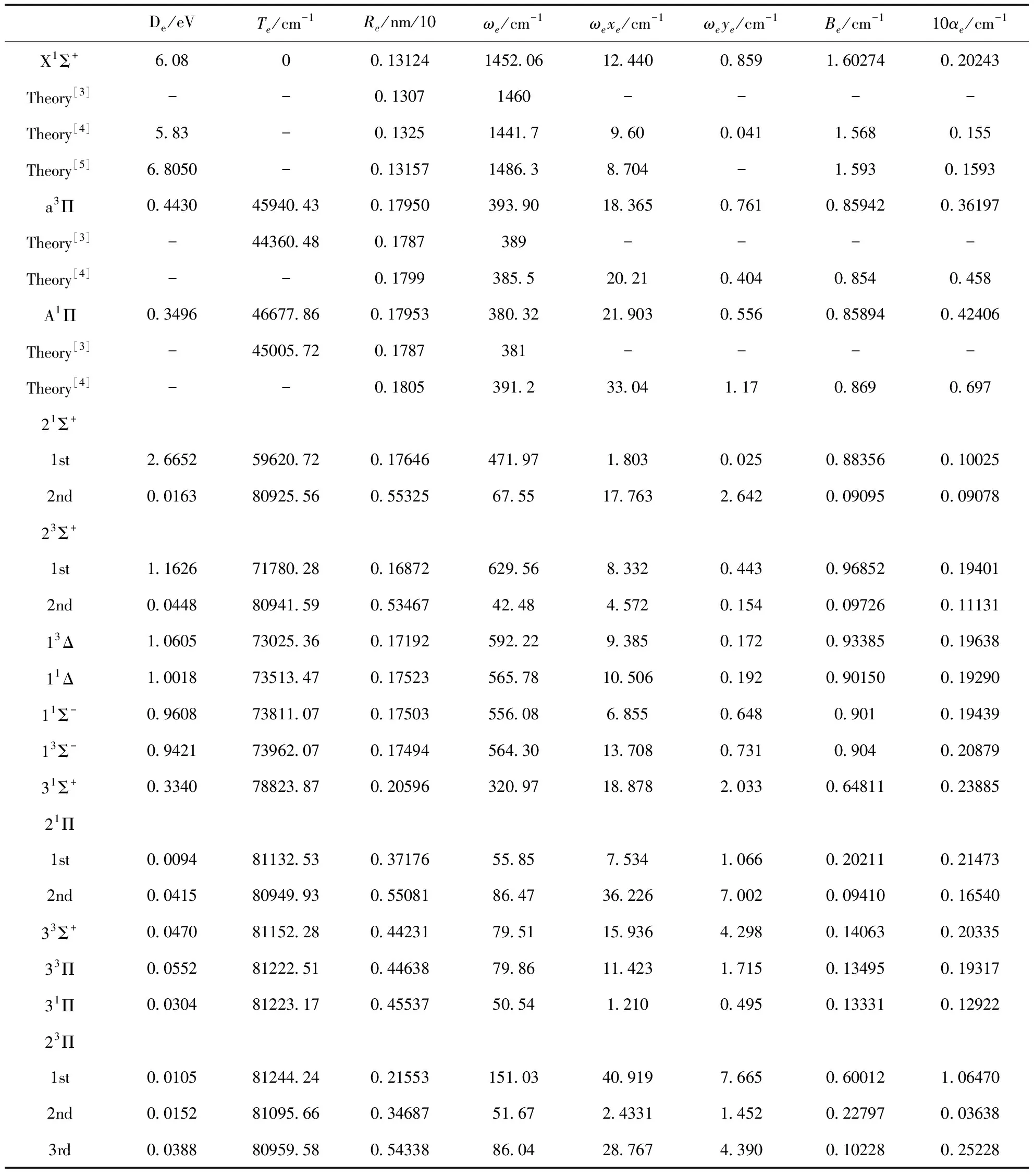
表1 在AV5Z基组下，考虑核价相关修正及相对论修正后计算得到的光谱常数

13Σ-态有34个振动态，振动能级278.82，818.82，1336.50，1834.91，2313.43，2771.11，3208.51，3625.08，4020.44，4394.18，4745.71，5075.54，5382.13，5665.30，5924.31，6159.01，6371.00，6557.82，6720.43，6860.78，6980.91，7080.76，7164.01，7234.31，7291.28，7340.71，7381.74，7412.81，7440.59，7463.91，7488.75，7519.89，7552.14，7583.43 cm-1.

31Σ+, 33Σ+, 33Π 和31Π态拥有较浅的势阱，De值分别为0.3340，0.0470，0.0552，0.0304 eV，这四个浅势阱有较少的振动态. 31Σ+态有20个振动态，振动能级156.02，445.84，716.20，967.15，1197.26，1405.32，1593.52，1757.58，1900.76，2024.98，2130.58，2217.95，2285.57，2333.62，2379.46，2431.92，2486.69，2543.98，2602.32，2660.14 cm-1. 33Σ+态有6个振动态，振动能级36.31，97.91，166.33，234.63，301.64，362.53 cm-1. 33Π 态有17个振动态，振动能级37.29，99.87，155.05，208.56，260.24，296.22，309.83，317.77，330.37，341.96，351.45，358.22，371.28，386.07，400.28，415.33，432.42 cm-1. 31Π 态有5个振动态，振动能级25.03，74.77，126.54，179.45，232.05 cm-1.

21Σ+, 23Σ+和21Π三个态具有双势阱，并且其他计算中均没有涉及，那我们有理由提供第一次的相关计算. 双势阱的产生是来自于其他态的势能曲线的影响. 从图1和表1可知，具有双势阱的三个态的第二个势阱非常浅，不易观察，并且均位于较大的核间距位置处. 21Σ+, 23Σ+和21Π三个态的第二个势阱分别位于平衡核间距5.5325，5.3467，5.5081 nm处，21Σ+态的第二个势阱的形成受到X1Σ+态的影响，为了避免交叉，从而使势能曲线的趋势发生改变，同样的23Σ+和21Π两个态的第二个势阱的形成也是分别受到了来自13Σ+和A1Π态的影响. 21Σ+, 23Σ+和21Π 三个态的第二个势阱处的能量均低于各自的无穷远处的能量，所以这三个态的第二个势阱都比较稳定.

23Π态作为十六个态中唯一的三势阱态，有三个极浅的势阱，在核间距2.1553 nm处的第一个势阱深0.0105 eV，在核间距3.4687 nm处的第一个势阱深0.0152 eV，在核间距5.4338 nm处的第一个势阱深0.0388 eV. 在实验以及理论研究中很难发现如此浅的势阱. 并且23Π态的第一个势阱处能量高于无穷远处的能量，这就使得第一个势阱并不稳定. 三个3Π态之间存在较强的相互关联作用，其它两个3Π 态对23Π 的影响导致了该态三个势阱的产生，微弱的影响并不能让我们对此现象有直观上的观察.

4 结 论

探究前两个离解极限的十六个Λ-S态的势能曲线，得到是十五个束缚态和一个排斥态，通过势能曲线计算得到十五个束缚态的相关的光谱常数，排斥态不做研究. 在0.082-0.9 nm核间距范围内，使用态平均完全活性空间自洽场(CASSCF)方法对初始猜测分子轨道和波函数进行优化，其后是用戴维森修正的icMRCI方法计算BeF+离子的十五个束缚态的势能曲线. 为了提高光谱常数的精度，在icMRCI理论水平上同时考虑核价相关和相对论修正. 分别计算了束缚态的振动能级. 通过BeF+离子前两个离解极限16个态的计算，为未来的实验和理论提供更广泛的光谱常数和分子常数.