土-隧道结构动力相互作用振动台模型试验中传感器位置的优选
2019-03-18,,,,,
,, ,,,
(1.河北工业大学 土木与交通学院,天津 300401;2.河北省土木工程技术研究中心,天津 300401; 3.南通大学 交通学院,江苏 南通 226019;4. 北京工业大学 建筑工程学院,北京 100124)
1 研究背景
随着我国城市化基础设施的发展及地下空间的开发利用,多交叉、小曲率、多密贴、越江跨海等复杂条件下的隧道工程日益增多,且地下隧道结构抗震设防所涉及的岩土动力学理论、灾变机理、数值仿真手段及多场耦合等问题会进一步增加地下结构抗震分析的困难程度[1-2]。然而,在进行复杂地质、工程条件下地下隧道抗震分析时,由于缺乏具有针对性场地的强震记录,地下结构的动力特性及灾变机理尚缺乏足够深度的认识,开展土-地下结构动力相互作用的振动台模型试验无疑是研究结构地震动力响应规律的最有效手段。
Chen等[3]开展了软土区浅埋矩形断面共同沟的纵向非一致激励振动台模型试验,得到了共同沟结构非一致地震激励的一些新规律;Masoud等[4]开展了地铁隧道对场地影响的振动台模型试验和数值分析,研究了地下结构存在对地基场域的放大效应;蒋树屏等[5]进行了西藏某地区跨断层隧道的振动台模型试验,分析了非均质断层中公路隧道衬砌结构的破坏规律及非均质断层对地震波在岩体内的传播影响;Chen等[6-7]开展了软土地区地铁地下结构的数值仿真和振动台试验,对地震动、加速度、孔压、地表震陷、结构应变、位移及空间效应进行了系统的研究;王明年等[8]通过三维数值分析与模型试验相结合的方式对高烈度区隧道支护体系内设置减震层效果进行了研究,为该地区隧道结构的减震设计提供了参考。然而,在振动台动力模型试验中传感器及位置优选对获得可靠试验数据十分关键,在此方面缺少较为有针对性的研究成果。
本文通过建立有限元-无限元耦合数值模型的方式对软土场地和地铁盾构隧道地震动力响应进行了分析,探讨了地基及结构地震反应特点,总结了振动台试验中隧道结构观测面位置的确定原则,以试验实测数据为基础分析了结构端部效应的影响,以期给出本次软土场地-地铁隧道动力相互作用振动台试验的主、辅观测面分布及主要观测指标,为试验数据采集及其他地下结构模型试验测点布置提供一定参考。
2 振动台试验加载设备
振动台试验加载设备的主要技术指标为:振动台台面尺寸3 m×3 m;最大有效载重10 t;工作频率范围0.2~50.0 Hz;最大倾覆力矩300 kN·m;最大偏心力矩100 kN·m;最大位移±100 mm;最大加速度1.2g。试验确定模型几何相似比为1/30,模型箱净尺寸为长l×宽b×高h=2.0 m×1.5 m×1.4 m,除去拟采用的侧壁维护结构、边界处理材料厚度及预留工作台面尺寸,试验模拟的原型地基场尺寸为l×b×h=55 m×45 m×40 m,盾构隧道模型采用水膏比为0.75的复合石膏及直径为0.5 mm的铁丝网片模拟,模型地基采用软弱土质相似材料进行填筑[9-10],模型试验系统如图1所示。

图1 振动台试验加载系统Fig.1 Loading system of shaking table test
3 工程概况及模型
以某软土场地典型盾构区间隧道为原型,埋深为17.9 m,衬砌厚度35 cm,外径尺寸6.2 m,内径尺寸5.5 m,幅宽1.5 m;衬砌管片采用C55P10混凝土,密度为2 400 kg/m3,弹性模量为35.5 GPa,轴心抗压强度为35.5 MPa,泊松比为0.2;管片中钢筋型号为HPB300级热轧钢筋,密度为7 800 kg/m3,泊松比为0.3;该区间段代表性场地土层分布如图2所示。

图2 土层分布及物理力学参数Fig.2 Geological distribution and physico-mechanical parameters
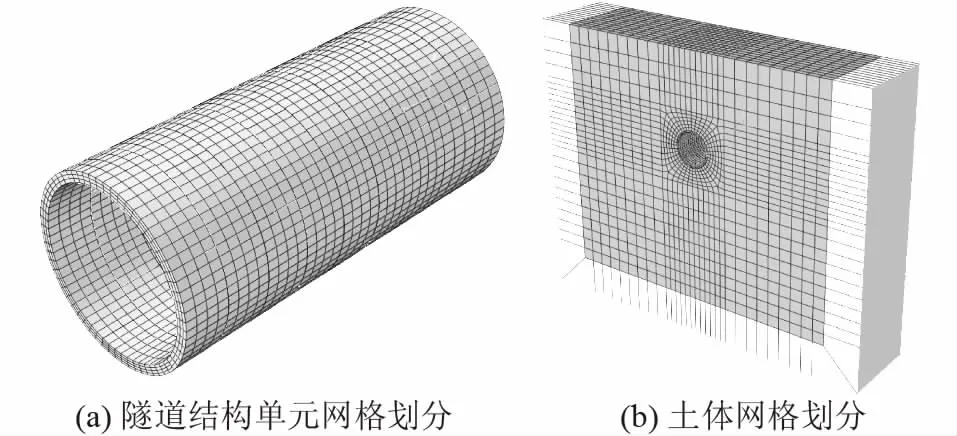
图3 土-地铁盾构隧道的计算模型Fig.3 Computation models of soil and metro shield tunnel
3.1 模型的建立
如图3所示,采用非线性有限元-无限元耦合建模方法,以有限实体单元分散混凝土结构及近场土体,以无限元模拟远场软土介质,消除模型的边界效应,建立土-隧道结构的三维数值模型,模型尺寸为124 m×68 m×13.5 m。
根据刘如山[11]文章中的结果,为保守起见,假设土-地下结构在变形过程中不发生分离,始终满足位移协调条件,通过设置绑定约束忽略土-隧道结构间的滑移和脱开现象。土体为C3D8R实体单元,采用D-P弹塑性本构模型;结构采用混凝土和钢筋分离式建模,混凝土采用ABAQUS自带的混凝土塑性损伤本构模型,钢筋采用Mises弹塑性模型。
3.2 地震波的选取
在模型底部沿水平向输入地震波,选取Taft波、天津波和LWD波作为输入地震动,其加速度时程及傅氏谱如图4所示。结合图5反应谱曲线可知,Taft波和LWD波频带稍宽,1~8 Hz间的频率成分明显,对应的反应谱特征周期主要集中在0~0.7 s内;天津波的频带较窄,0.1~1.5 Hz间的低频分量更为显著,长周期部分的放大系数明显比另2条地震波大。考虑地震强度对土-地铁盾构隧道相互作用的影响,将输入地震动峰值加速度分别调整为0.10g,0.15g,0.20g,0.30g,0.40g。

图4 输入地震波加速度时程及傅氏谱Fig.4 Time histories of acceleration and Fourier spectra of input seismic waves

图5 输入地震波标准加速度反应谱(阻尼比0.05)Fig.5 Standard acceleration response and spectrum of input seismic waves with a damping ratio of 0.05
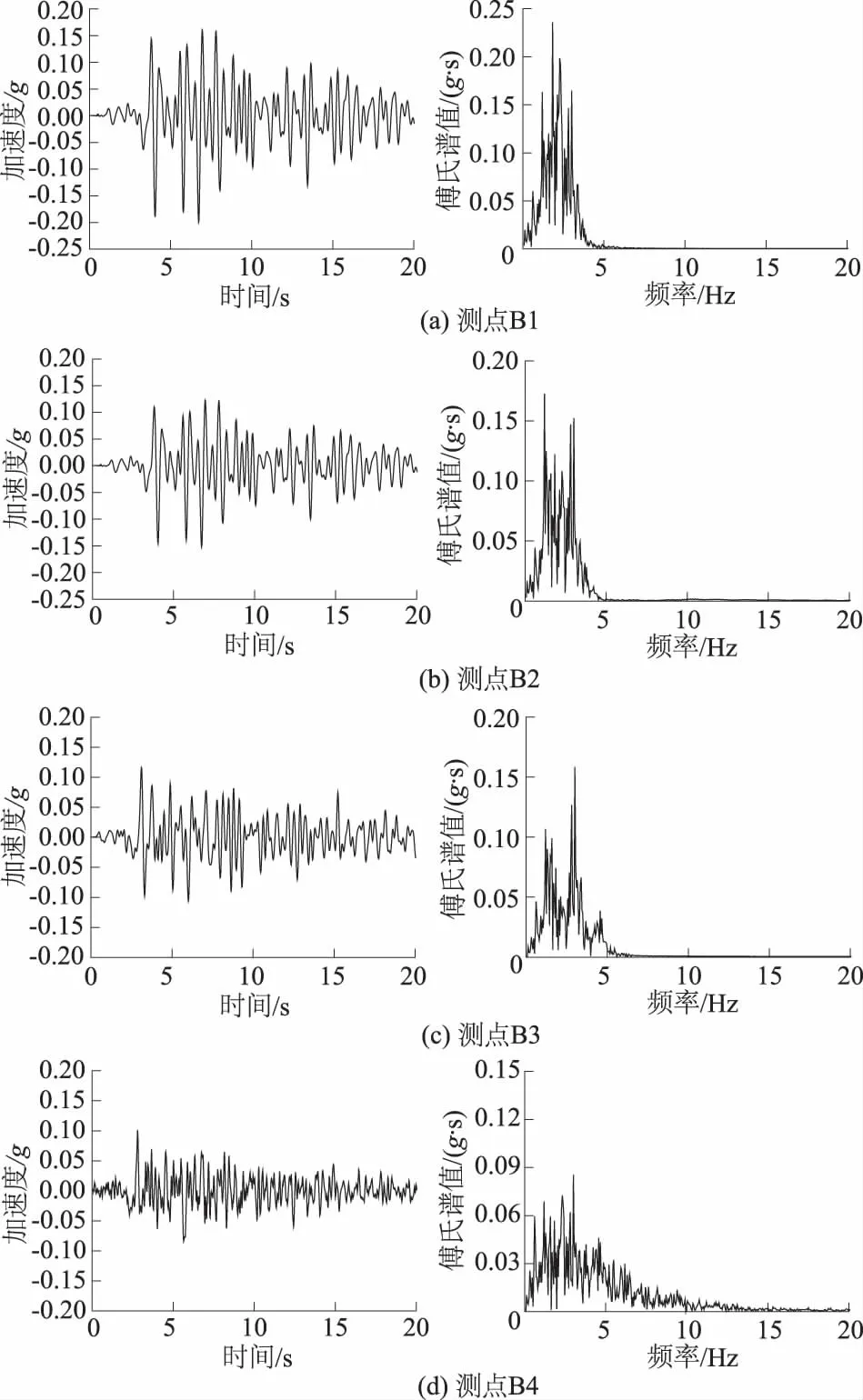
图6 输入天津波0.2g时的地基加速度时程及傅氏谱Fig.6 Time histories of acceleration and Fourier spectra of foundation in the presence of Tianjin wave 0.2g
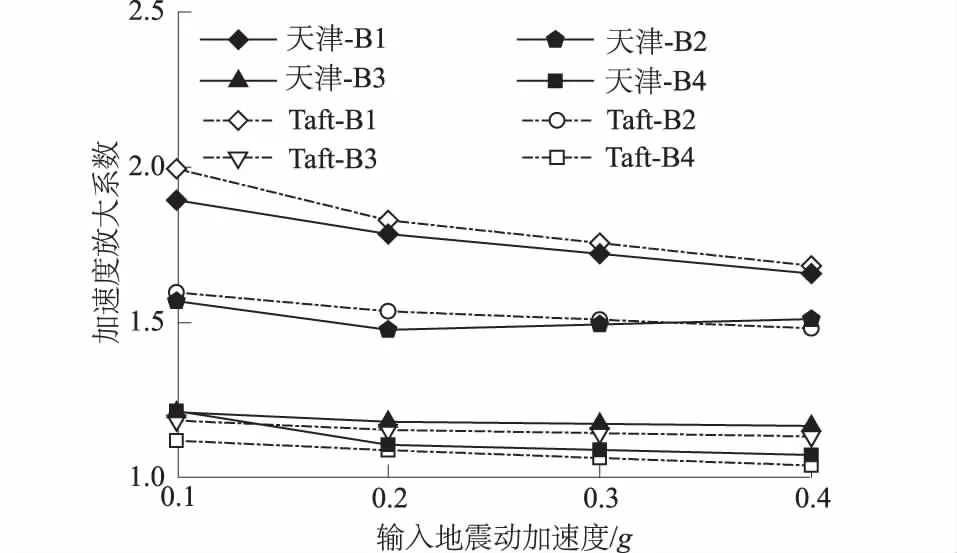
图7 不同输入地震波形下的加速度放大系数Fig.7 Amplification factors of acceleration in the presence of different input seismic waves
4 场地与结构地震响应分析
4.1 场地加速度响应分析
对地基场竖向中心线不同埋深处测点的加速度反应进行了监测,测点 B1,B2,B3,B4分别对应土体埋深0,10,34,60 m,输入天津波0.2g时的测点加速度及傅氏谱如图6所示。图7给出了不同加载条件下的加速度放大系数(AAF)沿深度的变化规律。由图6和图7可知,在地震波由下到上传播过程中,土体表现出了一定的高频滤波作用,0~4 Hz间的低频分量被放大,4 Hz以上的成分逐渐被过滤掉;指标AAF随埋深变化明显,越接近地表时其数值越大,测点B1的AAF值约为B4的1.5~1.8倍,且Taft波的AAF值在结构埋深以上稍大于天津波,在结构埋深以下稍小于天津波;整体上看,指标AAF随地震动强度的增大而逐渐减小,但减幅十分有限,2种波形下地表测点0.1g~0.4g加载过程中减幅仅为15.64%和12.46%;AAF值发展速率在结构埋深附近发生变化,试验时宜在结构不同位置处增设加速度传感器。
4.2 隧道结构地震响应分析
图8(a)—图8(c)为天津波0.2g作用下结构不同高度处的加速度时程及频谱特性,图8(d)给出了管片环向应力最大时刻的受力分布。

图8 天津波0.2g作用下隧道结构的地震反应Fig.8 Seismic responses of tunnel structure in the presence of Tianjin wave 0.2g
由图8(a)—图8(c)可知,在土-隧道结构动力相互作用下,模型结构不同高度处的频谱特性稍有差异,由下至上各测点的加速度频谱分量仍有低频放大及高频减小现象,这种规律与地基土中的规律一致,是由于结构受周围土体作用的影响;与同标高的地基测点相比,结构测点峰值加速度略小,其低频分量的傅氏谱值也较小。由图8(d)可知,与拱顶和仰拱成30°圆心角处的应力最大,拱顶、拱底次之,拱腰应力最小,且结构内、外受力状态相反。分析结果表明,隧道结构拱底、拱腰和拱顶处的峰值土压力互不相同,拱底最大、拱腰次之、拱顶最小,以拱底为基准,则拱腰和拱顶处的相对接触压力分别为0.83和0.76。因此,在对该结构或其他类似结构进行动力模型试验时,应对以上分析部位的应力、应变及接触动土压力情况进行重点观测。
5 振动台模型试验中传感器的布置
5.1 传感器的选择及布置原则
在土-地铁隧道动力相互作用的振动台试验中,应根据振动台设备、数据采集条件、模型比例和试验目的选择合适的数据传感器。加速度计、动土压计及孔压计宜选择质量轻、体积小、性能稳定的微型传感器,其平均密度宜与围岩相当,避免仪器与土体发生耦合振动;在传感器生产时,应做好接头处的防水保护和绝缘处理,数据连接线应保留足够传输长度,且宜选择细软、轻质类材料,避免线路过多而约束土体位移。
本次试验采集的数据主要有地表沉降及变形、加载设备输入加速度、台面实际反应加速度、模型箱体实际作用加速度、模型地基内部加速度响应、隧道结构加速度及动应变响应、土-隧道接触动土压力、地基土-侧壁动土压力和地基孔隙水压力。
选用的传感器分别为CF0410-3X微型加速度计、BWM16应变式微型动土压计、BWMK应变式孔压计、Panasonic HL-G112-S-J激光位移计和BX120-10AA光栅电阻应变片,数据采集系统为多台32通道DH5922N动态采集仪。
根据现有试验条件及数值分析结果,对传感器的选择及测点位置确定总结出以下几点要求[13-16]:
(1)传感器具有小体积、轻质、稳定的特点,避免仪器本身在加载过程中产生耦合振动。
(2)数据传输线应绝缘可靠、条理清晰,尽量消除对模型土体的约束和扰动,能够使布置有仪器的模型土近似模拟自由场地震动响应。
(3)模型地基观测面选取应与场域中线重合,避免激振边界影响,验证边界效应的测点不受此条件制约。
(4)隧道结构观测面应选择与纵向中心线垂直的横向断面,量测结果符合二维平截面假定。
(5)横向主观测面距离结构端部应>1倍结构宽度,结构端部效应观测面可<0.76倍结构宽度。
(6)结构观测面数量应≥2个,主观测面应≥1个,主观测面上的传感器数量多于其他观测面,辅助观测面上的重点部位布置方式应与主观测面一致,以便对数据采集精度进行检验。
(7)不同类型传感器在同一位置时,应协调各自相对位置,避免数据采集相互干扰。
(8)在隧道结构主观测面的关键位置内外布设应变片,可对比检验结构两侧受力状态。
(9)可以利用模型对称性减少测点布置,但在情况允许条件下,即使结构、荷载对称,也应根据试验本身需求适当增加测点。
(10)充分利用采集仪器通道的同时,合理分配不同种类传感器的接头位置。
5.2 传感器的布置方案
基于数值计算结果,在振动台试验中对隧道模型结构共设置了5个观测断面,其中1个观测面位于隧道结构端部,其余截面位于模型中部,每个截面都有针对性的进行传感器的布设。
如图9所示,端部观测面A—A距边界为0.26D(D为结构宽度),可用于检验激振方向上边界处理的可靠性,比较纵端边界约束对结构地震响应的影响;观测面B—B、D—D为主要观测面,辅助观测面C—C用于检测模型连接的可靠性,辅助观测面E—E距离端部1D,可与主观测面采集数据形成对比,验证数据的准确性;在主观测面上每隔30°圆心角布设应变片,用于量测结构应力状态,辅观测面上只在个别关键点处布设应变片。

图9 隧道模型结构观测面Fig.9 Observation sections of tunnel model structure
在模型地基中布置了11个加速度计、4个动土压力计和6个孔隙水压力计,其中加速度计A1—A4用于检验垂直激振方向上的边界处理效果,A5—A6用于分析平行激振方向上的边界影响,A7—A10用于分析地震波沿深度方向上的变化情况及结构对围岩土体的影响大小,A11为粘贴在模型箱外钢底板处的对比传感器,用于分析模型箱体实际受荷大小,检验模型箱体与台面固定可靠度;动土压力计P1—P4可用于分析土-侧壁接触土压力沿深度的变化情况;孔隙水压力计W1—W6用来量测结构周围土体的孔压变化。
试验系统传感器布置如图10所示,其中加速度传感器20个(A1—A20,其中隧道结构上9个)、动土压力计7个(P1—P7, 其中隧道结构上3个)、激光位移计4个(D1—D4)、孔隙水压力计6个(W1—W6),以及粘贴在隧道模型结构上的31片电阻应变片(S1—S31)。

图10 振动台模型试验系统测点布置Fig.10 Arrangement plan of sensors for the shaking table test
6 观测面端部效应试验结果分析
在本次土-地铁隧道动力相互作用振动台试验中,量测数据及加载工况较多,限于篇幅,本文只给出部分工况进行分析。
图11为工况LWD-0.2g加载时结构上部分测点的加速度时程及傅氏谱,此工况下箱体实际受荷测点A11峰值加速度为0.27g,出现在1.788 s,端部仰拱测点A12的峰值加速度为0.26g,出现在2.094 s,A15观测面峰值加速度依次为0.27g,0.27g,0.26g,0.26g,分别出现在0.163,1.766,1.766,0.163 s,隧道纵向测点整体加速度时程曲线基本一致,频谱特性并未发生明显改变,结构受周围土体的约束使得仰拱测点与箱体测点频谱特性稍有差异。

图11 工况LWD-0.2g下隧道结构加速度时程曲线 及傅氏谱Fig.11 Time histories of acceleration and Fourier spectra of tunnel structure in LWD-0.2g condition
图12给出了A12,A15,A16的加速度时程排序曲线[17],可以看出端部测点峰值加速度与中心断面基本相同,A—A观测面对应峰值加速度较中心断面大4.62%,但整体上端部加速度比中部稍小一些,误差保持在-4.62%~13.58%之间,侧面说明了试验时结构端部存在一定的约束效应。因此,在选择主、辅观测面时应尽量远离端部至少一倍结构宽度。

图12 隧道结构加速度时程排序曲线Fig.12 Sequential acceleration time history curves of tunnel structure
7 结 论
传感器的合理选择及测点的优化布置对能否在振动台试验中取得可信数据至关重要。本文以某软土地区地铁隧道工程为例,介绍了地下隧道振动台模型试验中的加载设备和数据采集系统,通过建立的有限元模型研究了软土场地及隧道结构的地震响应特点,总结了传感器布置时应遵循的原则,由此给出了振动台试验中整个模型系统的传感器布置方案,结合实际试验数据得到了以下几点结论:
(1)地震波在由基岩向地表传播过程中,峰值加速度响应逐渐增大,频率分量表现出扬高抑低的特点;地震动放大系数随地震动强度增大而减小,但减小幅度有限。
(2)结构不同高度处的频谱特性稍有差异,总体与周围地基运动特性保持一致,其应力反应在与拱顶、拱底成30°圆心角处达到最大,拱顶、拱底次之,拱腰应力最小,而接触动土压力则在拱底最大,供顶最小,以上位置可作为结构应变观测的关键点。
(3)结构端部约束效应较为明显,端部观测面峰值加速度较中心断面虽大,但整体上端部加速度反应比中部稍小,差幅保持在-4.62%~13.58%之间,观测面距离结构端部0.26D处的端部效应可达13.58%,约为观测面距结构端部1D处的3倍,在选择主、辅观测面时应尽量远离结构端部1D。
分析结果为试验的顺利开展奠定了基础,也可为其他地下结构模型试验测点布置提供参考。
