基于关键块体理论的岩体稳定性分析方法及其在三峡工程中的应用
2019-03-18
(长江科学院 水利部岩土力学与工程重点实验室,武汉 430010)
1 研究背景
块状结构岩体的变形、破坏模式主要是沿结构面滑动、结构面张开和块体脱离。对于块状结构岩体的破坏与稳定,块体间的相互锁定作用是一个十分重要的因素。许多块体不在临空面上出露,完全为其它块体所包围,不可能首先产生滑动。有的块体虽然出露于临空面上,但是出露部分小,埋藏部分大,一般也不可能首先失稳滑动。只有那些出露面大、埋藏面小,出露于临空面上的块体才是在形体上(几何上)可移动的块体。只有这些块体失稳、脱离后,周围的块体才有可能移动和失稳,因此这些块体的稳定性对于整个岩体的稳定性起着控制作用,被称为关键块体(key block)。各种块体结构中哪些块体是关键块体,与块体的几何形状、块体与临空面间的切割关系等有关。在给定了节理组参数的基础上,从数学上判断块体结构岩体中的关键块体是一个复杂的拓扑问题。
自1977年石根华在《中国科学》上发表《岩体稳定性的赤平投影方法》,以及1985年R.E. Goodman和石根华合作出版《Block Theory and Its Application to Rock Engineering》一书以来,块体理论作为岩石力学中研究岩体开挖面块体系统稳定性的一套理论体系已被国际上认同[1-2]。在块体理论体系的创建过程中,为将块体理论应用于实际工程,石根华博士编写了系列的块体理论程序。
三峡工程论证经历数十年,从早期的太平溪坝址地下厂房,到20世纪80年代三峡船闸高边坡的开挖稳定性论证,因复杂岩体结构面切割形成的块体稳定性问题,长期以来一直被作为工程建设论证过程中的一个重要技术问题。建立在岩体结构面全空间赤平投影和拓扑学基础上的关键块体理论,为解决三峡工程中岩体块体分析问题提供了新的分析思路。20世纪80年代,长江科学院董学晟及时跟踪关键块体理论及相关进展,随后任放、郭玉、邬爱清、黄正加、盛谦等结合三峡等工程岩体稳定性研究课题需求,对关键块体理论及程序进行了深入学习、消化及工程实用性开发研究[3-7]。经过“七五”国家科技攻关、三峡工程国家自然科学基金重大项目专题以及三峡工程科研等项目支持,解决了关键块体理论应用于实际工程的系列技术问题,如一般形状的块体体积等几何特征值计算、边坡上凹形块体几何构型以及考虑一般水压模式条件下的块体稳定性问题性分析等,实现了复杂岩体地质结构面切割条件下的关键块体识别及其稳定性评价,并应用于三峡船闸边坡及三峡地下厂房等工程部位的岩体稳定性分析与支护评价[8-12]。
本文在介绍关键块体及判别理论的基础上,重点总结了笔者所在团队在关键块体稳定性分析方面的相关研究成果,并展示了基于关键块体理论的岩体稳定性分析方法在三峡船闸边坡开挖过程中块体稳定性分析的应用效果。
2 关键块体及其判别理论
2.1 块体种类
根据有界性、几何可移动性和力学稳定性,块体可分为5种类型(无界块体、不可移动块体、稳定块体、潜在不稳定块体、不稳定块体),如图1所示。图中潜在不稳定块体和不稳定块体即是在几何上为有界可移动块体,在力学上是可能不稳定或不稳定块体。在块体理论中,这2类块体统称为关键块体。
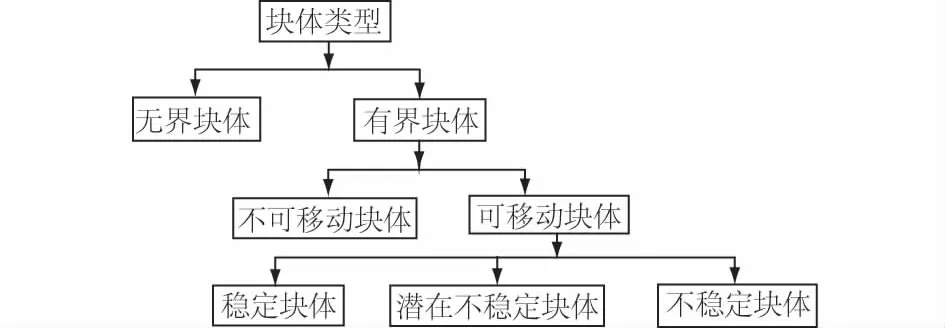
图1 块体分类Fig.1 Classification of block types
2.2 锥 域
考虑岩体中有m个结构面和k个开挖临空面。每个平面Pi将空间划分为上半空间和下半空间共2个半空间。一个凸形块体可以被认为是该m+k个特定半空间的交集。

2.3 基本定理
2.3.1 块体的有界性定理
一个凸形块体为有界的充要条件是其对应的块体锥域为空集或节理锥域完全属于空间锥域,即
BP=Ø 或 JP⊂SP 。
(1)
式中Ø为空集。
2.3.2 凸形块体几何可移动性定理
一个凸形块体,当其相应的块体锥域为空集,且节理锥域为非空集,则该块体为几何可移动块体;当其块体锥域为空集,节理锥域也是空集,则块体为有界的几何不可移动块体,反之亦然。可移动块体的充要条件可数学表达为
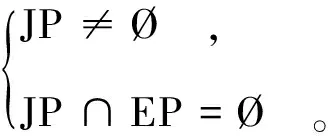
(2)
2.4 全空间极射赤平投影技术
块体理论中,将一般工程地质上用于表达结构面产状的平面赤平投影作图法,扩展成为全空间极射赤平投影法。全空间赤平投影将平面与投影参考球交线圆上的每个点都投影到参考圆所在平面上。块体理论中已证明,所有这些交线圆上的点,在参考圆投影平面上的投影连线组成一个投影圆,称为该平面的全空间极射赤平投影。
平面的全空间极射赤平投影圆具有一个很重要的性质(以下极点投影为例):平面的上半空间矢量投影在全空间极射赤平投影圆内,平面的上半空间矢量与全空间极射赤平投影圆内区域点相对应;平面的下半空间矢量投影在全空间极射赤平投影圆外,平面的下半空间矢量与全空间极射赤平投影圆外区域点相对应。对于上极点投影,则相反。
平面的全空间极射赤平投影的上述重要性质,使得块体理论在三维空间里的一些概念及定理可以用相应的二维全空间极射赤平投影区域或二维投影区域间的关系来表示,使块体理论的应用具有可操作性。如块体理论中各种类型的锥域在全空间极射赤平投影平面上对应相应的投影区域;块体的有界性和几何可移动性判断定理在全空间极射赤平投影平面上则是相应投影区域间的关系。
3 计算方法若干改进与完善
3.1 问题的提出
与关键块体理论相配套,石根华博士开发了系列的块体理论分析程序。这些程序在功能上主要体现在以下方面:
(1)块体类型及滑动模式判断。岩体开挖面上关键块体类型及在重力作用下的滑动模式,利用结构面及作用力全空间赤平投影图实现。
(2)三维关键块体几何形态识别。一般针对凸形块体,绘制块体各侧面在离坐标原点单位距离条件下的块体三维形态。若考虑各侧面的摩擦角,还可进一步分析各滑动模式下的稳定性(通常不考虑侧面黏结力的影响,无需块体几何尺度要求)。
(3)Londe图构建及其在关键块体稳定性分析中的应用。对任意节理锥,根据各侧面的法向矢量,可以构建三维空间条件下的所有滑动模式图,即Londe图,并用全空间赤平投影图展示与分析。
(4)关于隧洞最大关键块体区域及分析等相关程序。
综上所述,关键块体理论为我们提供了一套复杂岩体结构切割条件下,如何识别各类关键块体的理论法则,但针对某具体关键块体,在考虑组成块体侧面的结构面强度参数f及c、或考虑不同的侧面水压以及支护等复杂工程设计条件及措施时,不同类型关键块体的具体几何特征、含凹型块体在内的一般形状关键块体构型以及考虑侧面水压等条件下的复杂载荷计算等问题,仍是将关键块体理论应用于实践工程所面临的技术瓶颈。
3.2 计算任意形状块体体积的方法
岩体开挖面上出露的块体,根据其形状可分为“凸形块体”与“凹形块体”。块体中任意2点连线在该块体内,这种块体称为凸形块体;块体中任意2点连线不满足上述条件,称为凹形块体或组合块体。
三维凸形块体的体积可以通过将其分割成系列四面体的途径直接计算,这是原关键块体系列程序计算中推荐的方法。凹型块体则存在困难。在块体理论的实际应用中,由于岩体开挖边界通常比较复杂,如边坡台阶部位或洞室转角部位等,由此形成的块体在开挖临空面部位经常是凹形块体。为解决包括凹形块体在内的一般形状块体的体积及其他相关计算问题,笔者提出了以下计算一般形状块体体积的数值方法——块体侧面有向投影柱体体积叠加法[7]。
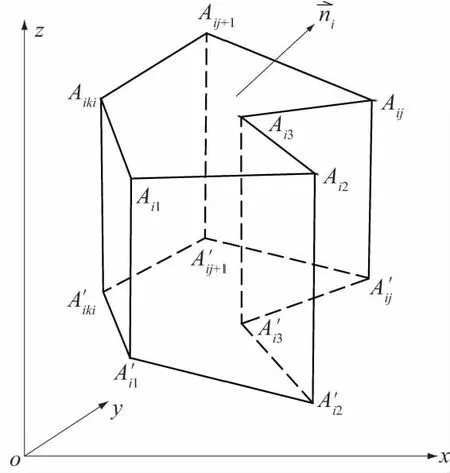
图2 块体侧面投影柱体Fig.2 Projective prism of block surface
该方法计算的基本思路是,在块体的m个角点中,找出其最小坐标z,记为zmin。将各角点均投影到z=zmin平面上,每一侧面有一闭合投影区域,各侧面与其相应投影区域之间构成一铅直柱体,称为该侧面的投影柱体,如图2所示。
根据侧面角点沿侧面边界顺序及侧面指向外侧法向矢量,计算该侧面的有向投影柱体体积,即
则任意块体体积为
(4)
式中n为块体的侧面数。
3.3 凹型块体(Ⅰ类)角点的识别方法
若凸形块体的某些部分被一个或多个凹形区域切割,且各凹形区域边界无凹向拐点,这样的组合块体为Ⅰ类凹形块体。以下给出Ⅰ类凹形块体的角点计算机识别方法[13]。对于一般形状的块体,另外还提出了一种“块体加与块体减”算法[14-15]。
对于凸形块体,取块体的任何一个侧面,块体的各个角点或者位于该侧面之上,或者位于该侧面平面的同一侧。判断凸形块体中,任意3个平面的角点是否属于块体的角点,可以通过构成指定块体的所有侧面的不等式方程确定,即设Ak(xk,yk,zk)为任意3个平面的交点,点Ak为块体角点的充分必要条件是,对块体所有的侧面Pi,下列不等式成立,即
aixk+biyk+cizk+di≥0,i=1,2,…,n。(5)
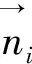
di=-aix0-biy0-ciz0。
(6)
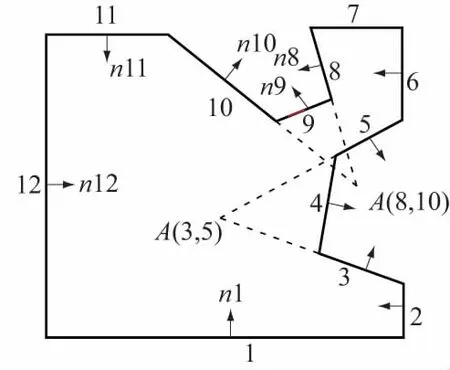
图3 凹形块体(Ⅰ类) 的角点识别Fig.3 Vertex identification of concave block (type Ⅰ)
对于凹形边界,块体有可能同时位于构成凹形边界某个侧面所在平面的两侧,因此判断某3个平面交点是否属于块体上的角点,不能简单用不等式(5)判断,但可以借助凸形块体角点的判断思路形成凹形块体角点的判断方法。
如图3,设块体的侧面数为n,其中,凸形边界侧面数为n1,凹形边界侧面数为n2。对于凹形边界的描述,设块体有m1个凹形区域,每个凹形区域由IQ(i)个侧面组成,且各侧面所在平面编号为IP(i,j),其中i=1,2,…,m1;j=1,2,…,IQ(i)。
对于任意3个侧面所在平面的交点Ak,判断点Ak是否属于块体上的角点,可通过以下2步判断实现。
(1)首先排除位于凹形区域Ωi凹侧内的角点,这里,Ωi∉{Ω1,Ω2,Ω3}。对于凹形区域Ωi,i=1,2,…,mi,且Ωi∉{Ω1,Ω2,Ω3},若对于凹形区域Ωi中的各侧面IP(i,j),不等式(式(7))成立,则Ak(xk,yk,zk)不属于块体上的点。
-ajxk-bjyk-cjzk-dj>0,
j=IP(i,1),…,IP(i,IQ(i)),
Ωi∉{Ω1,Ω2,Ω3} 。
(7)
式中Ω1,Ω2,Ω3为形成Ak交点的3个侧面所在的凹形区域编号。集合{Ω1,Ω2,Ω3}表示Ω1,Ω2,Ω3凹形区域编号的并集。利用式(7),可排除图3中的点A(8,10)。
(2)对于第一步未排除的角点,通过式(8)和式(9)判断某角点是否为块体上的角点。式(8)、式(9)同时成立为判断点Ak是块体角点的充要条件。
对于凸形边界侧面,有
aixk+biyk+cizk+di≥0 ,
i=1,2,…,n1。
(8)
对于凹形区域,Ωi={Ω1,Ω2,Ω3},且Ωi≠0,有
-ajxk-bjyk-cjzk-dj≥0 ,
j=IP(i,1),…,IP(i,IQ(i)) 。
(9)
利用不等式(式(8)和式(9))所表示的几何条件,可排除图3中的点A(8,10)和A(3,5)。其他凹形边界实线点,则同时满足式(8)和式(9)条件。
基于上述算法,绘制的三峡永久船闸三闸室中隔墩北墙的一个复杂块体几何构型,如图4所示。

图4 三峡船闸边坡出露的复杂块体Fig.4 Block with complex geometry exposed in the ship lock slope of Three Gorges Project
3.4 一般水压分布模式下的块体水荷载计算方法
对岩体块体稳定性起重要作用的因素之一是块体侧面裂隙水的作用。目前有关块体侧面裂隙水压对块体稳定性影响分析,主要是对四面体等简单块体在相应的水压分布模式条件下进行计算[16]。
实际工程中,块体形状一般非常复杂,且块体侧面上作用的裂隙水水位可以是任意情况。上述四面体块体侧面裂隙水作用下的稳定性分析方法,在实际工程应用中往往具有局限性。在块体裂隙面裂隙水水位为任意给定条件下,为了研究一般形状的块体(凸形体或凹形体)的稳定性问题,笔者提出了一种考虑块体侧面一般水压分布模式条件下的块体水载荷计算方法[8]。
一般水压分布模式条件下的块体水荷载计算的主要过程为:

图5 块体侧面水压多边形 及特征点Fig.5 Water pressure poly- gon and characteristic points on block surface
(1)根据块体侧面裂隙水位,确定该侧面上的裂隙水压多边形,以及块体侧面上位于岩体中裂隙水水位以下部分的面积。
(2)在块体侧面裂隙水压多边形上构建系列特征点,并根据上述特征点与岩体临空面(含水位面)相对位置及静水压力分布特性,确定各特征点的水压力值,如图5和图6所示。

图6 块体侧面水压分布模式Fig.6 Models of water pressure distribution on block surface
(3)根据某侧面上裂隙水压多边形特征点及相关连线上的水压力分布,将裂隙水压多边形划分为若干次一级六节点三角形区域。每一个六节点三角形区域可进一步划分为4个三节点三角形区域。按各三角形区域的平面水压分布计算所在子区域水压力大小,进而计算整个水压多边形内的水荷载大小。
(4)通过各侧面水荷载计算值,并考虑侧面法向方位,经有向叠加,可计算某一裂隙水位条件下块体所受的水荷载大小。
3.5 块体稳定性计算
3.5.1 块体合力计算
作用在块体上的力主要包括块体自重、块体侧面上的裂隙水压力及锚索锚固力等。块体合力的计算式为
(10)
3.5.2 块体滑动模式分析

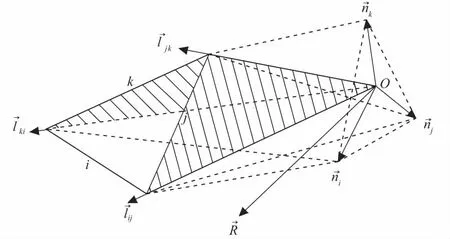
图7 块体滑动模式锥形区域划分Fig.7 Pyramid divisions for sliding models of block

3.5.3 块体稳定性安全系数计算
按照单面滑动或双面滑动不同滑动模式,根据矢量分解,计算块体合力在各滑动面上的法向和滑动方向上的力分量,并根据滑动面上摩擦系数f、黏结力c及滑动面面积,计算该块体相应的滑动安全系数[8]。
3.5.3.1 单面滑动
块体稳定安全系数K可按下式计算,即
(11)
3.5.3.2 双面滑动
块体稳定安全系数K可按下式计算,即
(12)
4 工程应用
自20世纪80年代以来,利用经逐步改进和完善的关键块体理论分析软件,先后开展了三峡永久船闸边坡(设计及施工阶段)、三峡临时船闸边坡(施工阶段)及右岸地下厂房(设计及施工阶段)等工程部位岩体关键块体识别和稳定性评价,解决了工程建设各阶段的相关技术难题。以下就关键块体理论在三峡永久船闸开挖施工阶段的应用及效果作简要介绍。
4.1 工程应用背景
三峡工程永久船闸是三峡工程的重要组成部分,布置于长江左岸山体中,为双线连续五级船闸。轴线方向NE111。船闸位于左岸山体中,人工开挖形成,开挖坡高一般50~120 m,最高达170 m。边坡下部为直墙段,高46~68 m。两线闸室之间为高5070 m的中隔墩岩体。
永久船闸直立闸槽开挖将在船闸南边坡和北边坡下部以及中隔墩两侧形成4个高度在50~70 m的直立坡段或边坡,其走向为NE111。由于岩体中结构面与直立边坡以及直立边坡上部水平开挖面(中隔墩表面、船闸南北坡直立坡段上部水平马道等)切割,使得在永久船闸下部直立闸槽开挖过程中,岩体中出露的块体问题一度成为高边坡设计与开挖施工中的关键问题。根据设计要求,对船闸开挖过程中边坡上出露的各类体积在100 m3以上的块体,需逐一验算其稳定性,并给出相应的加固处理方案。由于船闸边坡开挖形态复杂,开挖面上出露的各类块体形状绝大部分为非楔形体,有些还是凹形块体。用通常的以楔形体稳定性分析为目标的块体分析软件无法满足对各类形状的块体进行分析。为此,块体理论以及经适用化开发后的软件系列,在三峡船闸边坡中的块体稳定性分析及加固处理过程中发挥了重要作用,并先后对船闸直立槽开挖过程中的305个块体进行了几何特征、稳定性和加固处理措施分析,成果为设计所采用。
4.2 主要计算成果
三峡永久船闸开挖施工过程中,共揭露块体784个,其中,60%以上的块体方量不足100 m3,由于出露范围和规模较小,其失稳大多与开挖同时发生,对直立墙的形成与施工安全影响不大。根据地质调查结果,直立槽开挖期间揭示的体积>100 m3的块体有317个。在揭示的317个块体中,有12个块体已失稳,对余下305个块体按上述分析过程进行了逐一分析处理。图8为代表性块体三维图形。

图8 船闸边坡典型三维块体Fig.8 Typical blocks in the ship lock slope of TGP
305个块体体积与坡内埋深统计柱状图如图9所示,图中百分数为对应体积范围内的块体数量占总块体数量的百分比。不同计算工况条件下,各块体稳定安全系数统计柱状图如图10所示。
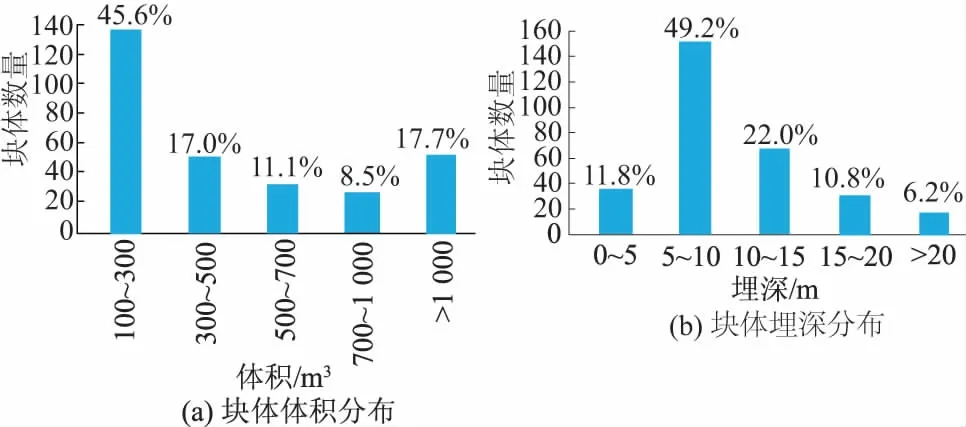
图9 块体体积和埋深分布统计柱状图Fig.9 Statistical histograms of block volume and block depth behind the excavation slope

图10 不同工况条件块体安全系数统计柱状图Fig.10 Statistical histogram of safety factor of block under different loading conditions
计算结果表明,三峡船闸边坡开挖过程中,由各类结构面切割形成的块体体积大多为100~500 m3,共有189个,占62.6;>1 000 m3的大型块体54个,占17.7,最大块体体积29 658.6 m3。埋深<10 m的块体个数有185个,占总数的61.0,且集中分布在5~10 m。
在稳定性方面,三峡船闸边坡设计确定的块体稳定性分析安全系数取值标准(考虑f及c值条件),在正常运行期安全系数取值为1.5,施工期及校核状态取值为1.3。对各块体逐一进行不同载荷条件下的稳定性分析,结果表明:在自重作用下,上述块体中有22个块体稳定性系数<1.3,需要进行加固处理;考虑锚索加固后,各块体稳定性明显提高,仅有3个块体的稳定性安全系数<1.3;水对块体稳定性影响很大,如果考虑块体高度一半的水荷载作用,在给定的锚索锚固力作用下,安全系数<1.3的块体数量有23个,占总数的7.5%。分析结论与现场实际块体出露特征与稳定状态总体相符合。
5 结 语
岩体的基本特征就是非均质性、各向异性以及不连续性。岩石地下洞室、边坡及坝基与坝肩等岩体工程开挖过程中,因复杂岩体结构面的切割形成的各种形态和规模的块体问题及其分析方法是岩石工程面临的基础性研究课题。长期以来,对于四面体等简单类块体构型与分析,已有不少的研究成果,但对于复杂岩体结构条件下的块体识别与分析,三峡船闸边坡开挖实践表明,各类方法都难以覆盖不同类型的块体,给工程设计带来不便。
基于全空间赤平投影技术及拓扑理论建立的岩体关键块体理论解决了复杂岩体结构条件下的关键块体判别难题,为岩石力学研究方法提供了全新的研究思想。基于关键块体理论的研究,并结合实际块体的稳定性分析需求,笔者在含凹形块体的一般形状块体体积计算、凹形块体角点识别以及块体侧面一般水压分布模型下的水载荷计算等方面进行了系统的工程实用性改进与完善。数百个关键块体的分析表明,三峡船闸边坡有关块体及稳定性分析结论与现场实际块体出露特征与稳定状态总体相符合,解决了工程建设中关于岩体结构块体稳定性评价与支护技术难题。另外,论文提出的基于关键块体理论的岩体稳定性分析方法具有较好的针对性和实用性,可以在工程实际应用中作进一步发展和完善。

