正交非线性渗流控制方程
2019-03-18齐成伟
齐成伟
重庆科技大学石油与天然气工程学院
笔者于2017年8月23至25日在第十四届全国渗流力学学术会议上作了题为《共形映射[1]真适用于正交非线性渗流场吗?》的特邀报告,通过介绍“正交非线性渗流定理”及其证明过程[2],对该设问式题名做出了除直流场外的否定回答。会议期间,笔者发现了证明过程中的几处阙漏,认为有责任提笔撰文补阙挂漏,以使正交非线性渗流定理的证明过程更加严谨,以期“共形映射不适用于除直流场外的正交非线性渗流场”这一认识成为非线性渗流力学的重大进展。
如何求得正交非线性渗流控制方程的一个曲流场符号解,为正交非线性渗流定理提供一个形象的例证,同时为理论非线性渗流力学奠基[3],是当前非线性渗流力学研究面临的最大挑战。鉴于这项挑战异常艰难,笔者力图将Descartes坐标系内的正交非线性渗流控制方程转换到既定问题相应的势流坐标系[4-5]内,以使汇源面、汇源线、汇源点一对一地重合到坐标面、坐标面族的极限线、坐标面族的极限点上,为挑战正交非线性渗流控制方程全空间曲流场符号解难题的科研工作者降低数学难度。
1 本构方程
1.1 正交幂比方程
描写低速非线性渗流之平行流的幂比方程[6]为
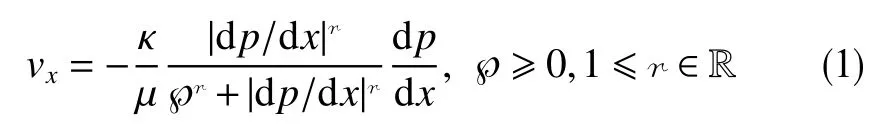
式中,v 为流体渗流速率,m/s;κ为多孔介质渗透系数,m2;µ为流体动力黏度,Pa·s;p 为流体压强,Pa;x(y 、 z)为Descartes坐标系O-xyz 的横(纵、竖)坐标(作为角标,示意方向),m;r为 非线性指数,无量纲;℘为渐近线截距,Pa/m。
易知,在Darcy坐标系O-(dp/dx)vx内 :若r=1,则幂比方程具有两条单向渐近线vx=−(κ/µ)(1−℘/|dp/dx|)dp/dx;若 r >1,则幂比方程具有一条双向渐近线vx=−(κ/µ)dp/dx 。
假设低速非线性渗流的等压面与流线正交,则其流体渗流速度与流体压强梯度的本构关系可写为正交幂比方程。矢量形式的正交幂比方程为
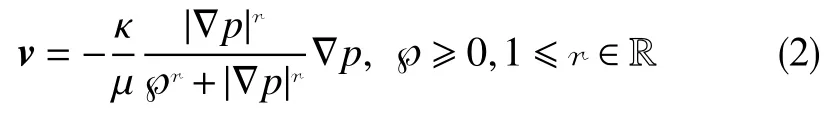
式中,v为 流体渗流速度,m/s。
1.2 福希海默方程
用以描写高速非线性渗流的福希海默(Philipp Forchheimer)方程[7]为
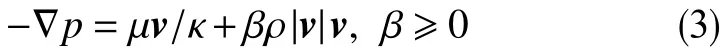
式中,β为福希海默系数与流体质量密度之商,m−1;ρ为流体质量密度,kg/m3。
为了便于代入连续方程,将式(3)转化为
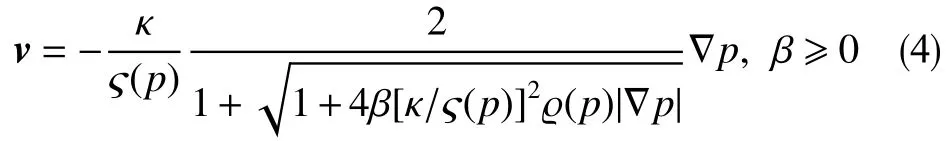
式中, ς (),ϱ()为可微函数; ς (p)为以流体压强为自变量的抽象流体动力黏度函数,Pa·s;ϱ(p)为以流体压强为自变量的抽象流体质量密度函数,kg/m3。
1.3 抽象本构方程
抽象正交非线性渗流本构方程为

式中, g (,,)为可微函数;g[ς(p),ϱ(p),|∇p|]为抽象非线性系数函数,m2/(Pa·s)。
式(2)、式(4)为式(5)的2种具体表达式,故分析式(5)所得定理及推论必定适用于式(2)、式(4)。
考虑多孔介质渗透系数随流体压强变化而变化的科研工作者可仿下文自行推导所需方程。
2 控制方程
2.1 抽象控制方程
将式(5)代入刚性多孔介质内单相流体渗流连续方程∇ϱ(p)·v+ϱ(p)∇·v+ϱ′(p)ϕ∂p/∂t=0,再将所得方程等号两端乘以−{ϱ(p)g[ς(p),ϱ(p),|∇p|]}−1,得实体形式的抽象正交非线性渗流控制方程

式中,ϕ为多孔介质有效孔隙率,无量纲;t 为时刻,s;(∇p·∇)∇p=∇(∇p·∇p)/2;p=defp(x,y,z,t)。
在Descartes坐标系内,式(6)中
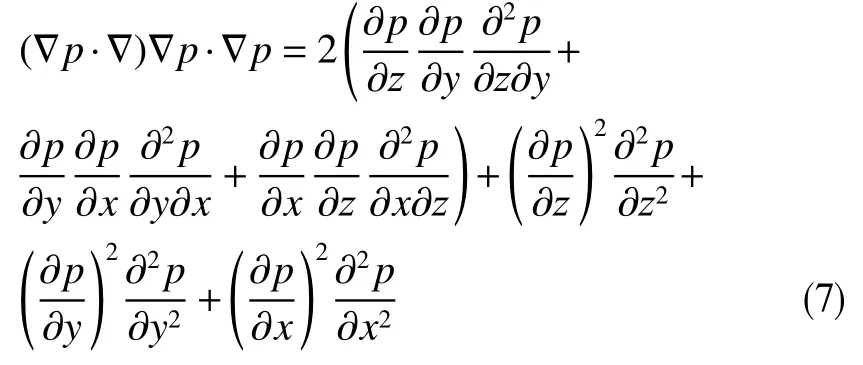
式(7)是二倍等压面平均曲率公式2kp=−∇·(∇p/|∇p|)=[(∇p·∇)∇p·∇p]/|∇p|3−∇2p/|∇p|中第一项的分子,而文献[2]式(20)的实部是 ( κ/µ)3与式(7)之积在二维Descartes坐标系O-xy内 的退化式。据此易知文献[2]式(23)确实为平面势流等势线曲率。
2.2 福希海默连续方程
对式(6)做替换g[ς(p),ϱ(p),|∇p|]→[2κ/ς(p)]/{1+[1+4βκ2ς−2(p)ϱ(p)|∇p|]1/2},得
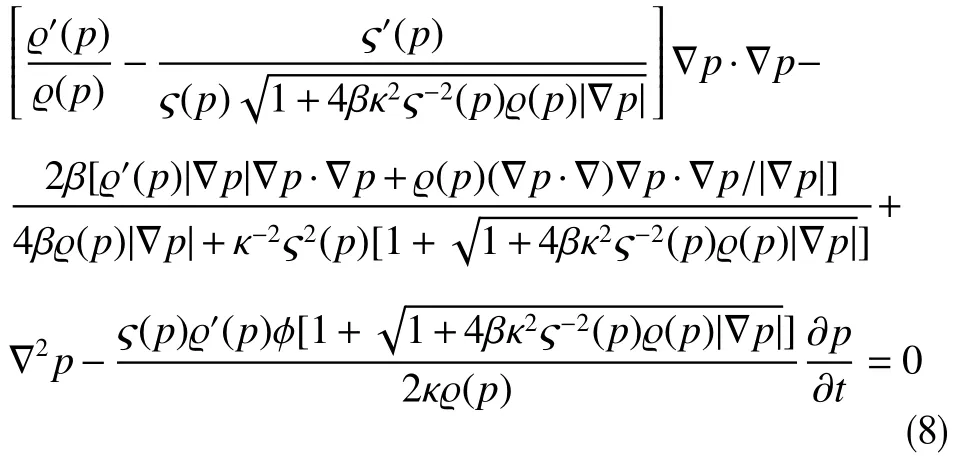
称式(8)为实体形式的“遥望物理梦想方程(Equation Unrelated to Physics Dream)”。
将∇p·∇p=|∇p|2、|∇p|=[(∂p/∂z)2+(∂p/∂y)2+(∂p/∂x)2]1/2、∇2p=∂2p/∂z2+∂2p/∂y2+∂2p/∂x2和式(7)依序代入式(8),得
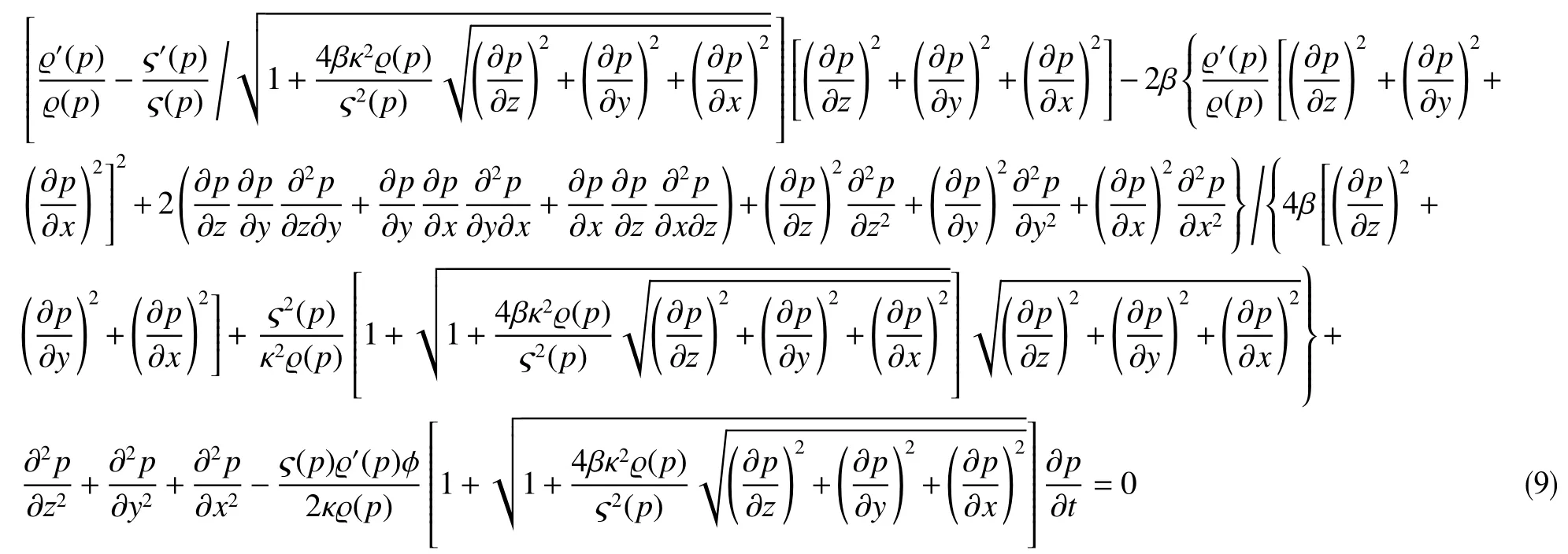
称式(9)为“笛卡尔坐标系遥望物理梦想方程(Equation Unrelated to Physics Dream in Cartesian coordinate system)”。
遥望物理梦想方程便是正交高速非线性渗流控制方程。
2.3 正交幂比连续方程
对式(6)做替换 ς (p)→µ、ϱ (p)→ρ和g[ς(p),ϱ(p),|∇p|]→(κ/µ)|∇p|r/(℘r+|∇p|r),化简后再将所得方程
|∇p|2(℘r+|∇p|r)等号两端乘以,得实体形式的正交幂比连续方程
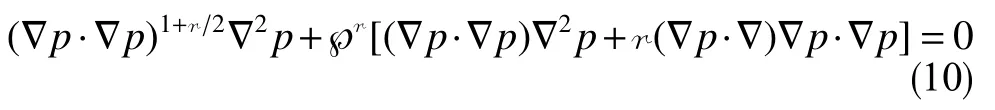
将∇p·∇p=|∇p|2、|∇p|=[(∂p/∂z)2+(∂p/∂y)2+(∂p/∂x)2]1/2、∇2p=∂2p/∂z2+∂2p/∂y2+∂2p/∂x2和式(7)依序代入式(10),得Descartes坐标系内的正交幂比连续方程
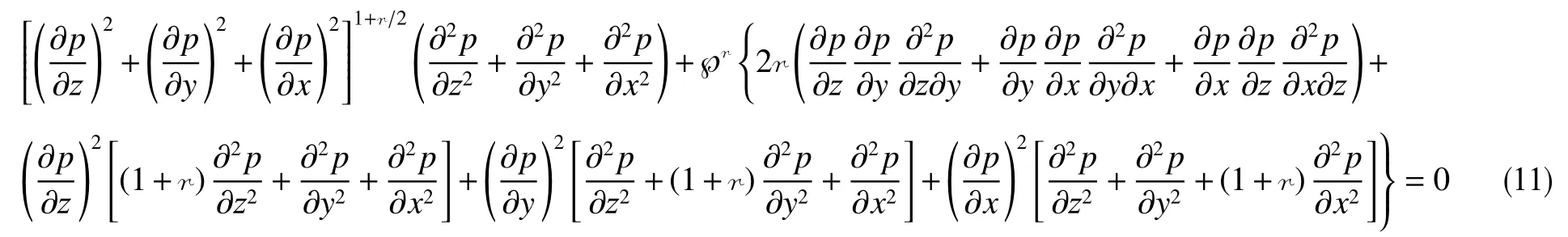
正交幂比连续方程便是正交低速非线性渗流控制方程。
3 流场几何
3.1 叠加原理不适用于非线性渗流场
正交非线性渗流控制方程属于二阶拟线性偏微分方程,而叠加原理仅适用于线性偏微分方程,故叠加原理不适用于非线性渗流场。
应用叠加原理之前须求得待求场汇源流分布。例如无限大等厚均质各向同性水平多孔介质层内等势水平直线段汇激发的流动的宏观流场函数无法由无限大均质各向同性多孔介质内等势水平直线段汇激发的流动的宏观流场函数通过线性叠加得到,因两宏观流场内直线段汇处流体流出分布[8]不相同。
3.2 共形映射不适用于多孔介质正交非线性曲流场
“正交非线性渗流引理”的证明过程中,有
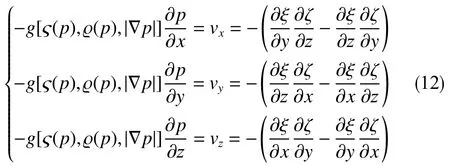
式中, ξ =defξ(x,y,z,t)、 ζ =defζ(x,y,z,t)为流面函数。式(12)每行第2个等式因v=−∇ξ×∇ζ而成立。与文献 [2]相比,符号差异处以本文为准,下同此约。
令ζ=z ,则式(12)退化为
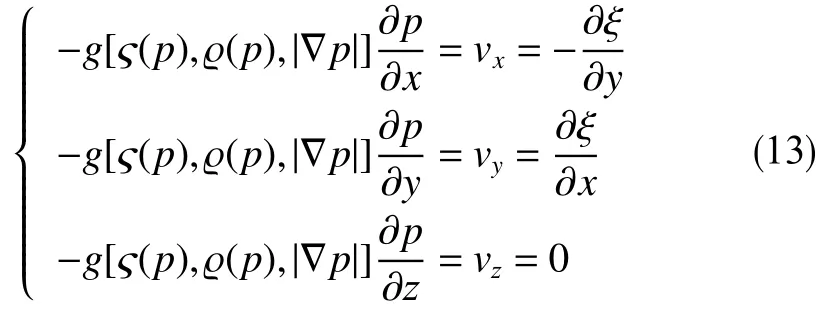
与共形映射的充分必要条件,即Cauchy-Riemann方程组
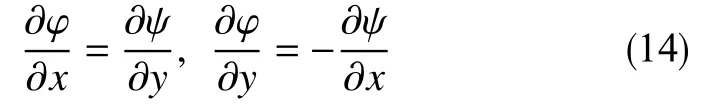
相比,正交非线性渗流的压强函数与流面函数关系方程组多了抽象非线性系数函数,即g[ς(p),ϱ(p),|∇p|]。
若可微线性化函数φ=φ(p)(及其导函数dφ/dp=φ′(p))存在,即
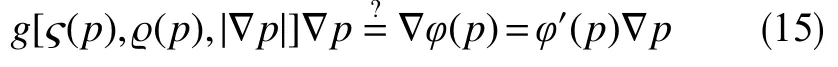
成立,则式(13)可转化为Cauchy-Riemann方程组,进而共形映射间接适用于可转化为线性渗流场的正交非线性渗流场。
对式(15)第1个等号两端做旋度运算,有

事实上,对于直流场(kξ∩ζ=0)和曲流场(kξ∩ζ0),有
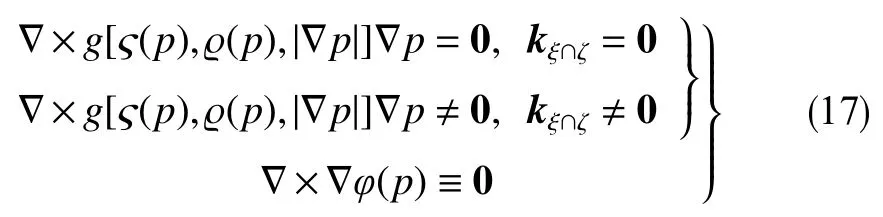
式中,kξ∩ζ为流线曲率矢量,m−1。式(17)第1行和第2行由下文式(20)得出。
据式(17)和式(16),式(15)被明确为
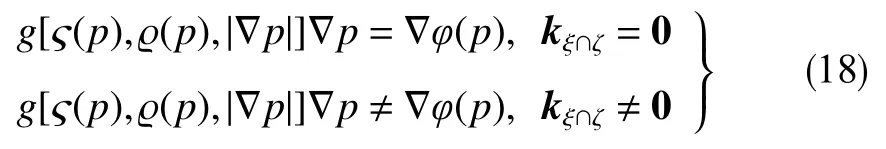
式(18)显示:对于除曲流场外的正交非线性渗流场,可微线性化函数φ=φ(p)(及其导函数dφ/dp=φ′(p))存在。
再若可微非线性化函数p=φ−1(φ)的具体表达式易被求得,则可将由共形映射或解Laplace方程所得势函数φ=defφ(x,y,z,t)的具体表达式代入可微非线性化函数p=φ−1(φ)的具体表达式而得到除曲流场外的正交非线性渗流压强场函数p=φ−1[φ(x,y,z,t)]的具体表达式,如下文从式(47)到式(48)。
式(18)与式(13)相结合,得“曲渗定理(nonconformality theorem on nonlinear flow field with curved streamlines):共形映射不适用于除直流场外的正交非线性渗流场。”曲渗定理亦可通过Riemann映射定理与正交非线性渗流定理相结合而得出。
本文未研究“拟共形映射(quasi-conformal mapping)”与正交非线性渗流场的关联性问题。
3.3 正交非线性渗流定理
“正交非线性渗流之直流速度场为无旋场;正交非线性渗流之曲流速度场为有旋场。”此谓正交非线性渗流引理。
“假设非线性渗流的等压面与流线正交,若流场为曲流场,则相同条件下单相不可压缩或可压缩流体非线性渗流与单相不可压缩流体线性渗流的流线形状不同。进而,等压面形状亦不同。”此谓正交非线性渗流定理。
现裨补正交非线性渗流引理和正交非线性渗流定理证明过程中的阙漏。
将文献[2]式(5)中(κ/µ)g(|∇p|)更正为g[ς(p),ϱ(p),|∇p|]后,文献[2]式(6)变更为
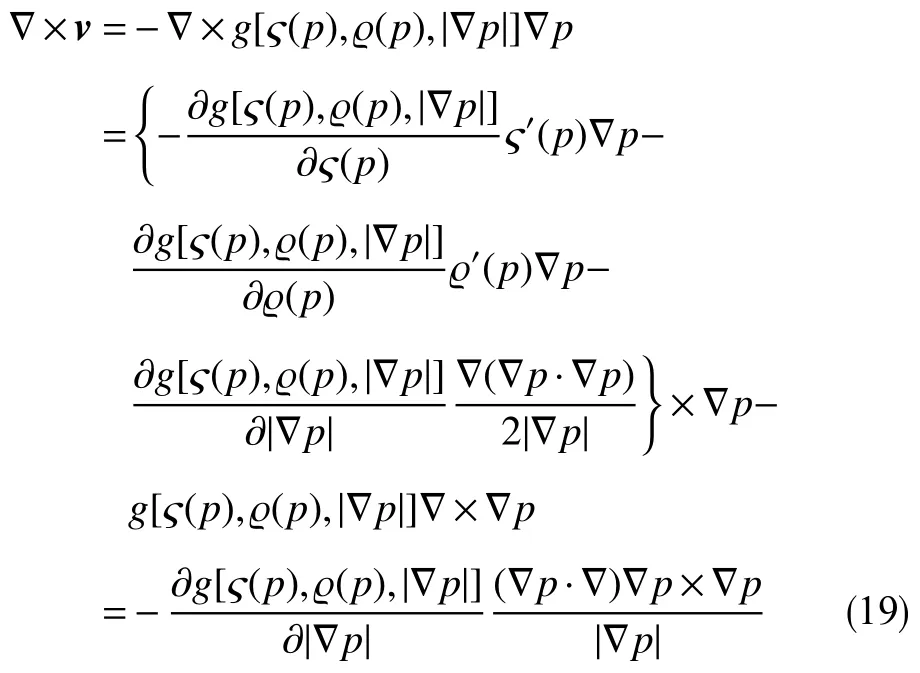
可见,有旋与否依然仅取决于(∇p·∇)∇p×∇p 。
将文献[2]式(11)更正为本文式(12)后,文献[2]式(15)不受影响。
将文献[2]中从式(16)起倒数第6、5行中g′(|∇p|) 0 、 kξ∩ζ={µ/[κg′(|∇p|)|∇p|3]}Ω×∇p 更正为∂g[ς(p),ϱ(p),|∇p|]/∂|∇p| 0、kξ∩ζ={∂g[ς(p),ϱ(p),|∇p|]/∂|∇p|}−1|∇p|−3Ω×∇p后 ,文献[2]式(16)变更为
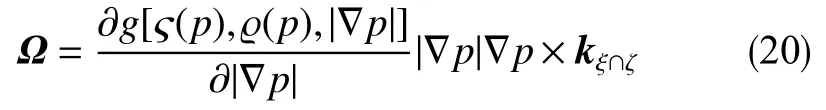
式中,Ω为流体渗流涡度,Ω=∇×v,s−1。
显然,正交非线性渗流引理正确。
将文献[2]式(27)、文献[2]式(33)中(κ/µ)g(|∇pn-l|)更正为g[ς(pn-l),ϱ(pn-l),|∇pn-l|]后,文献[2]式(32)不受影响且文献[2]式(33)中第3行等式依然成立,因而正交非线性渗流定理正确!
可利用“异极坐标系闭合坐标线生成式x→{s2+x2+y2−[(s−x)2+y2]1/2[(s+x)2+y2]1/2}/(2x),−s 正交非线性渗流定理还原了非线性渗流的先天复杂性。 沿着“易先于难,简先于繁,特殊先于一般”的科学研究途径,创建理论非线性渗流力学宜先研究空间单直线汇、空间对偶直线汇直线源、空间单平直带汇激发的稳态正交非线性流场。为了便于与线性渗流作对比和流域边界条件设定,现将二维Descartes坐标系内的正交非线性渗流控制方程转换为由既定问题相应的线性渗流流网形成的无竖维势流坐标系内的正交非线性渗流控制方程。 本文仅研究平面稳态流场,故水平流面函数ζ(x,y,z,t)=z 可 略,铅垂流面函数ξ(x,y,z,t)可记为ψ(x,y)。 平面稳态线性流场(含渗流场)复势 p 与复坐标z 的抽象函数关系为 式中,f( )为解析函数;φ为势,m2/s;ψ为流,m2/s。对于渗流场,φ=κ(p−po)/µ。其中,po为零势压强,Pa。 “平面稳态势流场运动学通式”[9]中,无竖维势流坐标系度量张量的协变分量公式为 水平势流坐标系内的压强梯度模平方项、压强Laplace项、二倍势流等压面平均曲率分子项依序为 式(23)和式(6)显示:将Descartes坐标系正交非线性渗流控制方程转换为水平势流坐标系正交非线性渗流控制方程的关键是求水平势流坐标系度量张量的协变分量gφφ(或与之相等的gψψ)。 4.1.1 空间单直线汇势流坐标系 无限大等厚均质各向同性水平地层内铅垂贯穿地层的一口正圆井激发的线性渗流场的复势公式为 式中,lc为特征长度(如正圆井半径),m。 分离式(24)等号两端的实部和虚部,得 式(24)的逆函数为 分离式(26)等号两端的实部和虚部,得 将式(26)代入式(22),得 4.1.2 空间对偶直线汇直线源势流坐标系 无限大等厚均质各向同性水平地层内铅垂贯穿地层的两口采注流量相等的正圆井激发的线性渗流场的复势公式[4]为 式中,s 为环布井群成圆半径,m;θ为任意一口卵圆井或唯一一口正圆井围绕井群形心 z˜ 逆时针偏离实轴正向的弧度,rad;z˜为井群形心复坐标,z˜ =x˜+iy˜, m。 分离式(29)等号两端的实部和虚部,得 式(29)的逆函数为 分离式(31)等号两端的实部和虚部,得 将式(31)代入式(22),得 式(33)中,θ,x˜,y˜,lc消失,不是偶然。 4.1.3 空间单平直带汇势流坐标系 无限大等厚均质各向同性水平地层内铅垂贯穿地层的一口椭圆井(或一条狭长椭圆裂缝)激发的线性渗流场的复势公式[5]为 式中,l为椭圆井壁面焦线距或长球井壁面焦点距,m。 分离式(34)等号两端的实部和虚部,得 式(34)的逆函数为 分离式(36)等号两端的实部和虚部,得 将式(36)代入式(22),得 将式(23)代入式(8),删除含 z项和含t项后再将所得方程等号两端乘以 gφφ,得无竖维势流坐标系稳态正交高速非线性渗流控制方程 称式(39)为“无竖维势流坐标系稳态遥望物理梦想方程(steady-state Equation Unrelated to Physics Dream in planar potential-stream coordinate system)”。 4.2.1 空间单直线汇势流坐标系福希海默流 将式(28)代入式(39),得易于描述空间单直线汇激发的福希海默流的空间单直线汇势流系遥梦方程 对于空间单直线汇势流坐标系极线 (−∞,ψ,z)处的直线汇激发的福希海默流,流场具有绕竖轴的旋转不变性和沿竖轴的平移不变性。将∂p/∂ψ=0,∂2p/∂ψ2=0代入式(40),得 4.2.2 空间对偶直线汇直线源势流坐标系福希海默流 将式(33)代入式(39),得易于描述空间对偶直线汇直线源激发的福希海默流的空间对偶直线汇直线源势流坐标系遥望物理梦想方程 4.2.3 空间单平直带汇势流坐标系福希海默流 将式(38)代入式(39),得易于描述空间单平直带汇激发的福希海默流的空间单平直带汇势流坐标系遥望物理梦想方程 将式(23)代入式(10),删除含 z 项后再将所得方程等号两端乘以得无竖维势流坐标系正交低速非线性渗流控制方程 4.3.1 空间单直线汇势流坐标系正交幂比流 将式(28)代入式(44),得易于描述空间单直线汇激发的正交幂比流的空间单直线汇势流坐标系正交低速非线性渗流控制方程 对于空间单直线汇势流坐标系极线 ( −∞,ψ,z)处的直线汇激发的正交幂比流,流场具有绕竖轴的旋转不变性和沿竖轴的平移不变性。将∂p/∂ψ=0,∂2p/∂ψ2=0代入式(45)后再将所得方程等号两端乘以(∂p/∂φ)−2,得 方程式(46)在双曲非线性(r=1)情况下的符号解为 将对式(47)进行量纲分析所得CⅠ=−q3κ/()、式(25)、=r 依序代入式(47),得 式中,r 为柱极坐标系的径坐标,m。 式(48)便是已经求得的柱极坐标系双曲非线性柱径流简约压强场函数,即文献[6]式(4)。文献《正交低速非线性渗流场仿真》介绍了式(48)的应用。 4.3.2 空间对偶直线汇直线源势流坐标系正交幂比流 将式(33)代入式(44),得易于描述空间对偶直线汇直线源激发的正交幂比流的空间对偶直线汇直线源势流坐标系正交低速非线性渗流控制方程 4.3.3 空间单平直带汇势流坐标系正交幂比流 将式(38)代入式(44),得易于描述空间单平直带汇激发的正交幂比流的空间单平直带汇势流坐标系正交低速非线性渗流控制方程 (1)以平面线性渗流的等差等势线和等差流线为网格线,对以该平面线性渗流内外2条等势线为等压出入流边界的平面正交非线性渗流流域进行剖分,则在二维Descartes坐标系内对(闭曲线形)等压出入流边界赋予压强值被转换为在相应无竖维势流坐标系内直接对内外2条坐标线赋予压强值。得到无竖维势流坐标系稳态正交非线性渗流压强数值解柱径流压强场函数测定所用数值解法的准确度。采用何种先进的偏微分方程数值解法才能获得精准的正交非线性渗流压强数值解是创建计算非线性渗流力学所面临的关键技术难题。 (2)欲创建理论非线性渗流力学,宜先探寻能间接获得正交非线性渗流压强场函数(或速度场函数)的某种未知映射。若探寻无果,则将不得不面对势流坐标系正交非线性渗流控制方程,从而不得不求助于更高深的偏微分方程理论以直接求控制方程的符号解。通过Legendre变换,可将类似于极小曲面方程的二维Descartes坐标系正交幂比连续方程转换为线性椭圆型偏微分方程。对此感兴趣的科研工作者可检索求极小曲面方程符号解的方法以资借鉴。拟线性椭圆型偏微分方程的变分方法或可一试。p(φ,ψ)后经逆坐标转换得到二维Descartes坐标系稳态正交非线性渗流压强数值解p(x,y)。可用双曲非线性4 势流表象
4.1 势流标架


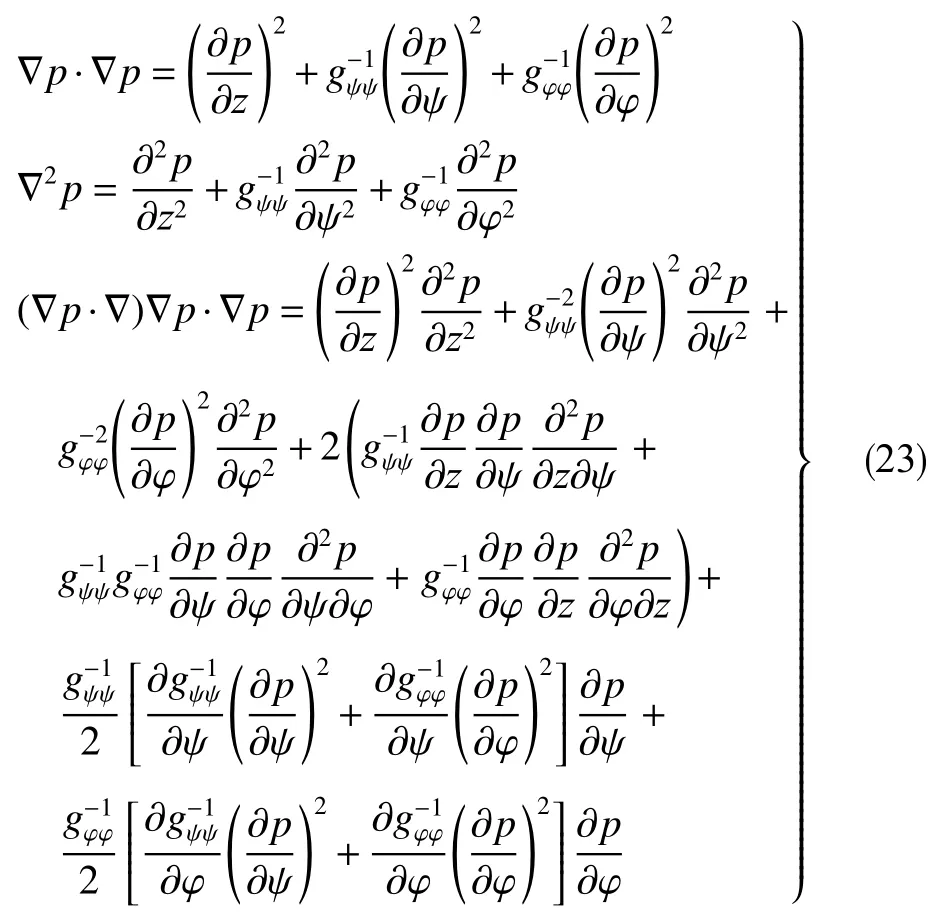



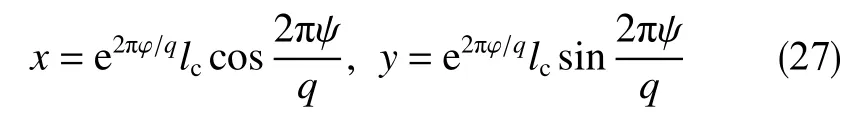

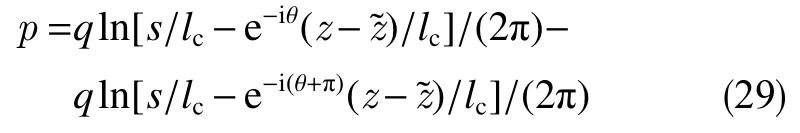
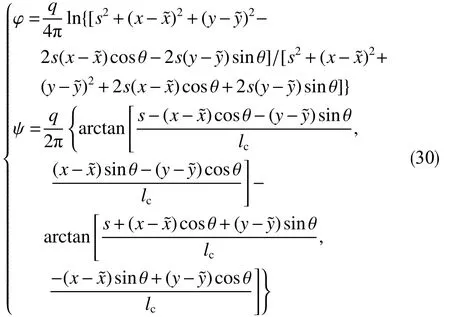
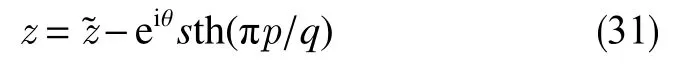
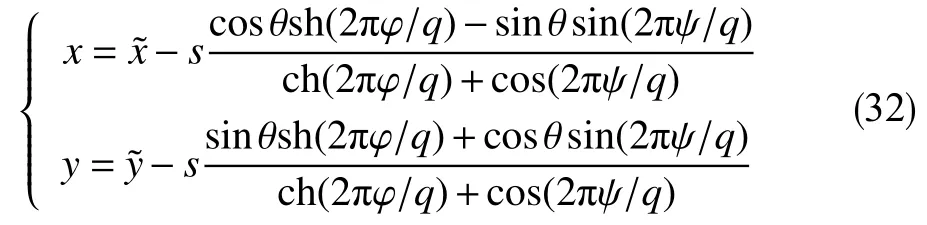
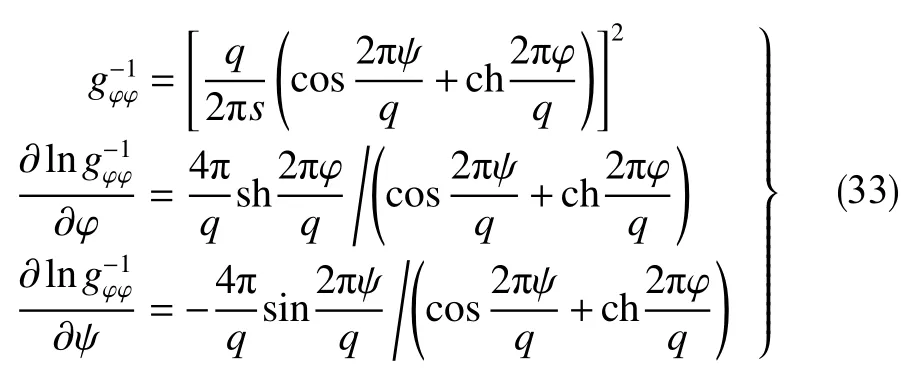

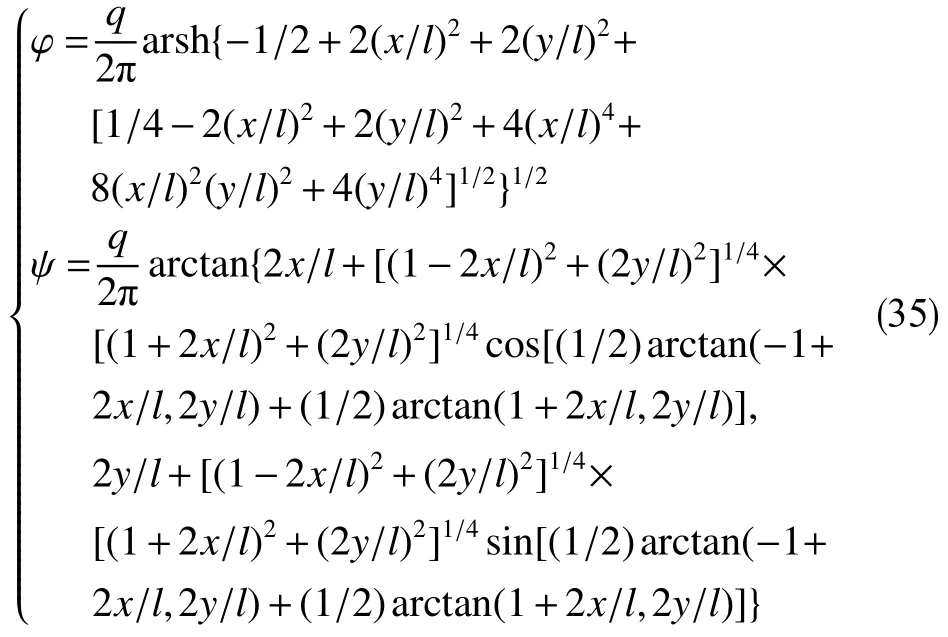
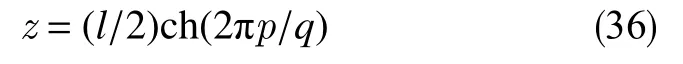

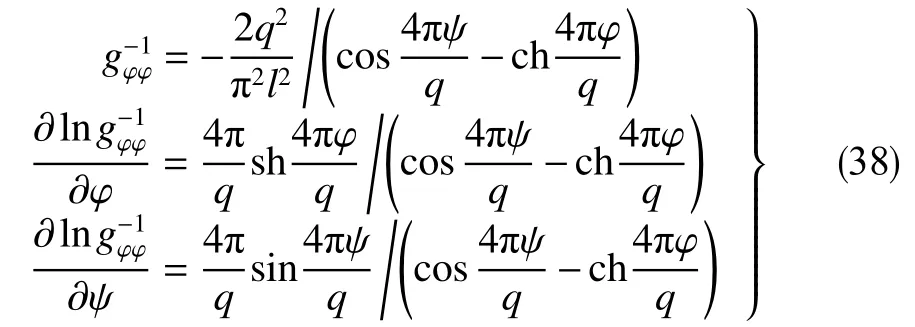
4.2 无竖维势流坐标系稳态福希海默连续方程
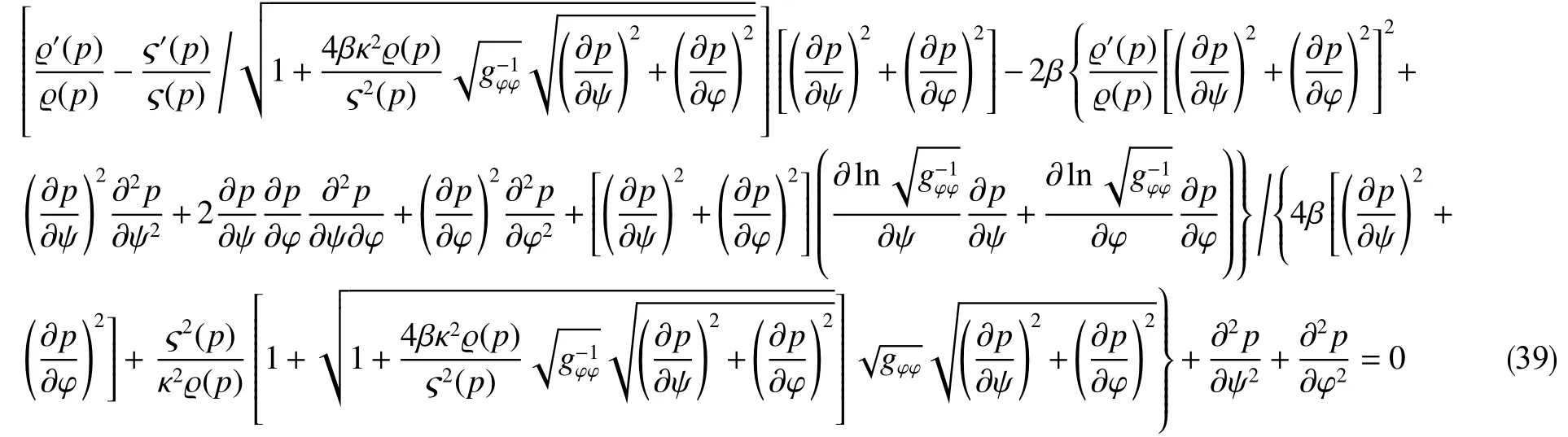
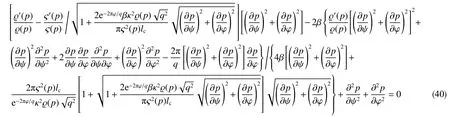



4.3 无竖维势流坐标系正交幂比连续方程
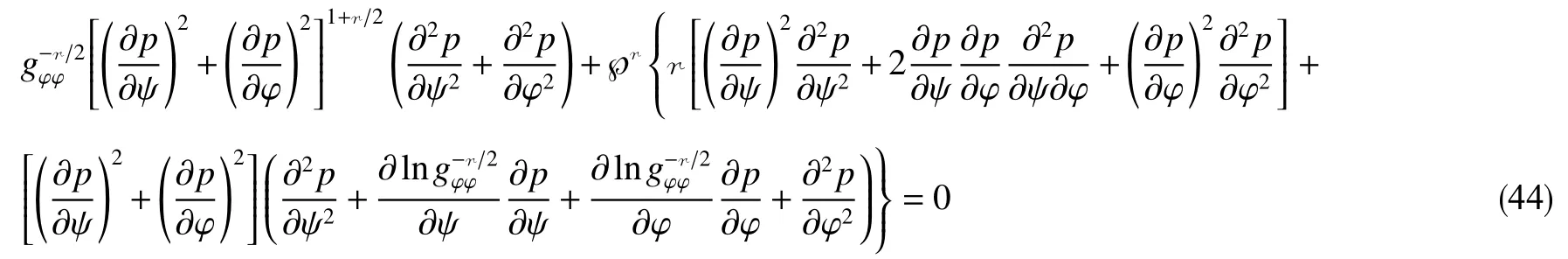
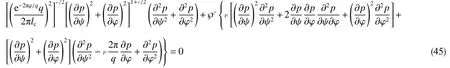
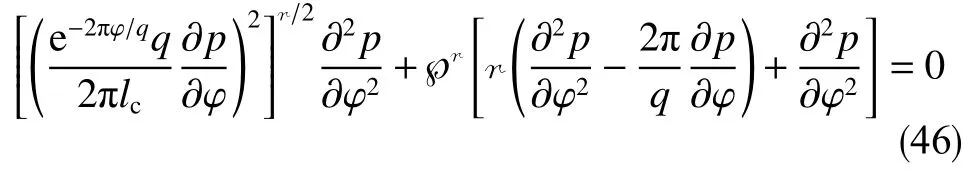
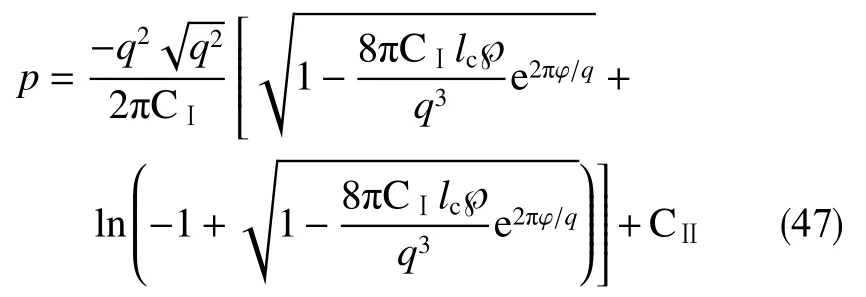
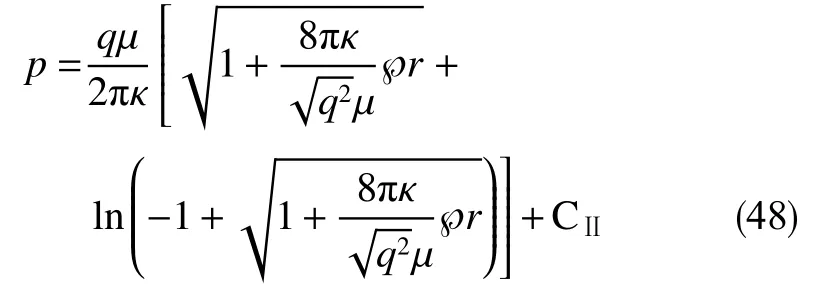
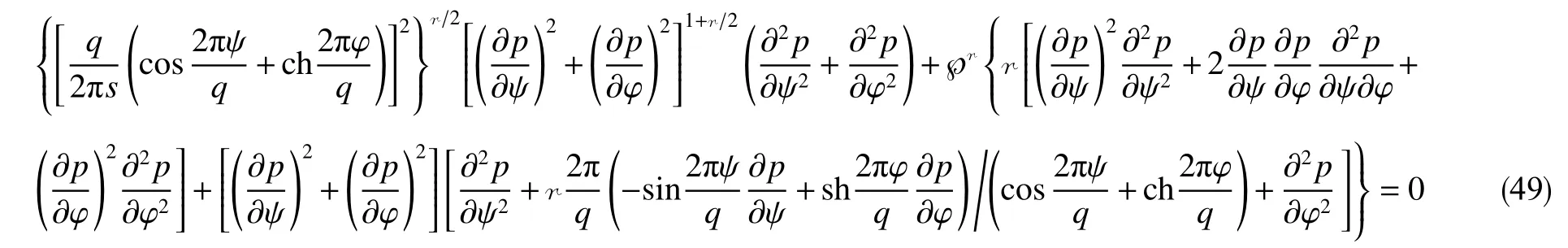
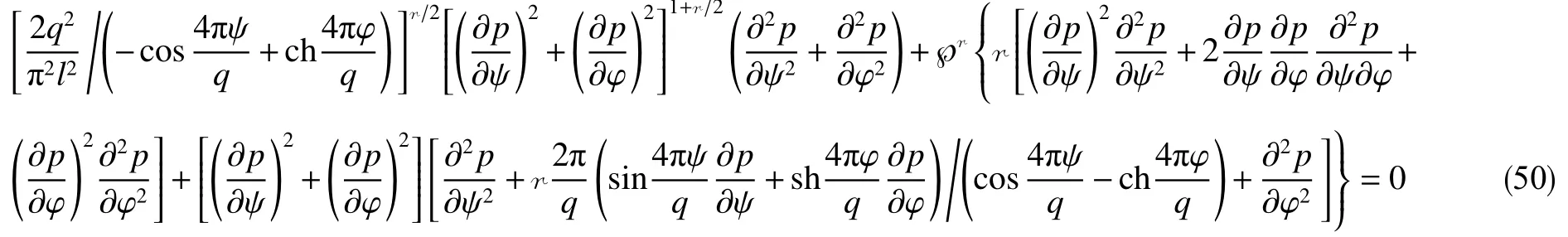
5 结语
