基于数理统计的铁道车辆车轮轮缘厚度旋修值研究*

2019-03-18李春林江亚男杨文喜宋冬丽刘瑞军吴华丽

铁道机车车辆 2019年1期

李春林，江亚男，何平，杨文喜, 宋冬丽，杜彪, 刘瑞军，吴华丽

(1 神华铁路货车运输有限责任公司榆林车辆维修分公司, 陕西神木 719300；2 西南交通大学，成都 610031；3 中铁科学研究院有限公司，成都 610032)

尽量少的维修成本和尽量高的安全性一直是轨道交通研究者追求的目标。为实现车轮经济旋修的目的，各国分别研制了旋修用系列轮缘厚度踏面模板[1-3]；日本研究者奥山雅贵[4]基于大量现场数据，制定了车轮旋修量判定基准及车轮踏面均匀、正确旋修的具体方法；董孝卿等[5]通过长期跟踪和分析京津城际铁路CRH3C型动车组车轮磨耗、车辆振动性能，提出了新的系列薄轮缘车轮形面设计原则，研制了系列薄轮缘车轮外形，并通过仿真计算和线路试验，证明了新设计的系列薄轮缘车轮外形踏面的有效性；李秋泽等[6]针对CRH5型车运行120万km后参照原旋修形面进行旋修存在旋修量大、车轮使用寿命降低明显的问题，通过分析该型车大量的120万km后的车轮参数情况设计了XP55-28经济型旋修踏面，并通过仿真分析对该形面进行验证；庞松林[7]根据CRH1、CRH2型车LMA型踏面经济旋修需求，设计了LMA-28型薄轮缘踏面外形，进行了设计型面的动力学性能验证和磨耗动力学性能验证，并对CRH2型车旋修周期和车轮检测限值进行了优化。前人在薄轮缘旋修模板和轮径旋修量旋修决策理论研究方面做了大量工作，但关于轮缘厚度的最优旋修量研究工作鲜见报道，且未有相关的轮缘厚度旋修量确定原则。

以大量运营数据为基础，深入研究车轮踏面的磨耗特性，并探索了一种合理确定轮缘厚度旋修量的方法：通过长期跟踪运营单位的列车轮对几何状态数据，基于统计分析理论研究新旋和服役到期车轮轮缘厚度随机样本的分布规律及其所反映的磨耗特性，并采用线性“灰箱”映射关系模型进行了列车车轮服役过程的刻画，以保障服役后参数未超限可靠度为约束条件，确定不同车型车轮的轮缘厚度最优旋修量。

1 轮缘厚度分布规律研究

1.1 轮缘厚度定义与特性

铁道机车车辆通过走形部件——轮对沿着既定的钢轨线路运行，轮对车轮形面的几何外形关系到轮轨接触关系的好坏，对整个车辆系统的服役性能影响显著。随着轨道交通的发展，车轮踏面外形先后由圆柱形踏面、锥形踏面发展至凹形踏面(圆弧形踏面、磨耗形踏面)。目前世界各国普遍采用的为磨耗形踏面，图 1为典型的磨耗形踏面廓形。

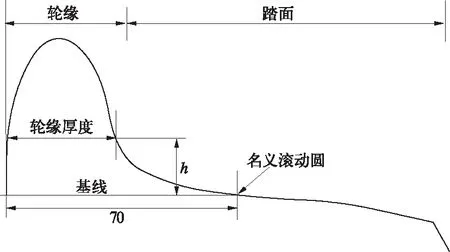
图1 机车车辆磨耗形车轮踏面廓形

磨耗形踏面包含轮缘和踏面两段，由多段圆弧与直线拼接而成。其中，踏面段为具有一定锥度的拼接曲线，车辆通过曲线时通过左右两轮锥度引起的轮径差引导轮对顺利通过，减轻轮轨磨耗；轮缘为保持车辆沿钢轨运行，防止车轮脱轨的重要部分。轮缘厚度值为距离名义滚动圆基线高度h处对应的轮缘厚度值，不同踏面类型对应的h不同。

车辆运行过程中轮轨间的滚动摩擦必然导致车轮形面的磨耗。由于轮缘厚度值为以基线相对位置为基准测量的厚度值，该值受轮径和轮缘磨耗的双重影响，其变化规律具有一定的随机性。笔者前期研究发现[8]，轮缘厚度值变化与踏面和轮缘磨耗有如图 2所示的相对关系。即在新轮(/新旋车轮)与钢轨磨合期(阶段Ⅰ)，轮轨踏面接触点位置横移量大，易形成两点接触状态(轮缘接触点、踏面接触点)，轮缘磨耗较大；在稳定期(阶段Ⅱ)，轮轨踏面接触点基本稳定于名义滚动圆附近，踏面磨耗逐步加深，引起轮缘厚度测量点基准位置下移。总的而言，轮缘厚度值变化量由式(1)描述。

y=h-cx

(1)

式中h为测试位置轮缘厚度的真实磨耗量；c为单位轮径减小量导致的轮缘厚度增大量；x为轮径磨耗量；y为轮缘厚度变化量。

图2 轮径与轮缘厚度磨耗规律

1.2 概率分布与假设检验理论

鉴于轮缘厚度值样本的随机性，文中基于统计分析理论，采用概率分布函数实现对轮缘厚度值的描述。选用正态分布进行轮缘厚度样本的统计推断，其概率密度函数表达式如式(2)所示[9]。

(2)

式中ρ为概率密度；σ为样本均方差；σ2为样本方差；μ为样本均值；x为样本。正态分布的分布函数，即样本的累计频率函数表达式如式(3)：

(3)

式中，F(xm)为样本数字低于xm的累计概率。

对样本所提出的统计推断需进行假设检验，以证明这一假设准确性。采用单样本Kolmogorov-Smirnov检验(K-S检验)方法[9]进行轮缘厚度样本的正态性检验，即通过样本的经验累积分布函数F(xm)与假定的理论分布函数F0(xm)进行比较，以此判断该样本是否服从这一分布。具体过程为：

(1) 提出原假设和备择假设

原假设H0：F(xm)=F0(xm)⟺

备择假设H1：F(xm)=F0(xm)

(2) 确定检验统计量及其分布

对K-S检验，其检验统计量为如式(4)所示。

(|F(xi-1)-F0|(xi)|,|F(xi)-F0(xi)|)

(4)

式中，Z为检验统计量;F(xi)、F(xi-1)为样本经验累积分布函数；F0(xi)，F0(xi-1)为假定的理论累计分布函数。

(3) 选择检验的显著性水平α

假设检验是基于小概率原理的推断，但多小的概率才算小概率，这并无统一规定，常见的情况为0.10,0.05,0.01,0.001几个等级。文中基于前期研究经验，取显著性水平α为0.01。

(4) 根据样本数据计算检验统计量的实现值

将样本数据带入检验统计量计算公式，计算得到检验统计量的一个实现值。

(5) 计算检验的p值并判断

检验的p值是指在原假设成立的前提下，检验统计量等于第(4)步骤计算的现实值或更极端情况的概率。显然，p值越小，意味着在原假设成立的前提下发生了小概率事件，因此有充分的利用拒绝原假设。

(6) 检验判断

以事先确定的显著性水平α来衡量p值的大小，若p>α，则不能拒绝原假设。反之，若p<α，则拒绝原假设。

1.3 轮缘厚度分布函数

文中依次调研了某铁路货车公司5年内的段修数据，某铁路局动车段2年内的专项修数据和某铁路局机务段机车的3年内段修数据。并采用1.2节理论进行数据的分布拟合和假设检验。

以铁路货车为例，对78 701个货车左侧车轮轮缘厚度样本进行分布拟合，并对拟合函数进行K-S检验，其分布拟合图 3所示，表 1为K-S检验结果。由表1可见，样本正态性检验的显著性水平大于0.01，不能拒绝原假设，因此可以认定轮缘厚度值样本服从正态分布，即x：N(μ，σ)，且有：

旋修前样本：N(31.044,1.409),旋修后样本：N(29.673,1.192)

表1 轮缘厚度的拟合分布函数拟合的K-S检验

图3 重载货车轮缘厚度分布拟合(左轮)

依次采用1.2节的理论对铁路货车、机车及动车组的轮缘厚度值样本数据进行统计分析，表 2为不同类型车轮轮缘厚度分布拟合结果。

表2 轮缘厚度分布函数拟合

分析表 2中各类车型统计分布函数的均值和方程可见：

(1) 重载货车：由分布函数可见，该单位服役的铁路货车车轮旋修前轮缘厚度均值明显大于旋修后，该类车轮轮径磨耗显著，这是由于铁路货车重载，且其运营线在平原地区，曲线段少；服役一个段修周期，左侧车轮轮缘厚度值明显大于右轮，表明该系列车辆存在偏磨现象，这是由于该单位列车始终服役于固定的专用线造成，建议在段修周期中期调换左右轮，减缓左右轮偏差。

(2) 高速动车组：该动车段车辆轮对服役后轮缘厚度略有增加，该车轮对以轮径磨耗为主，且不存在明显的偏磨。

(3) 铁路机车：该单位铁路机车轮对服役后轮缘厚度明显减小，其车轮以轮缘磨耗为主，这是由于该单位机车运营线路位于西南山区，曲线段比例高且曲线半径小；该单位列车不存在明显偏磨显现。

由以上分析可见，由于铁道车辆运营线路、负载情况不同，车轮磨耗特性存在偏差，在进一步的旋修策略研究中应充分考虑各运营单位的差异性，基于历史数据分析规律制定合理的旋修策略。