基于模糊控制的防滑控制方法研究*

曹宏发

(1 中国铁道科学研究院集团有限公司 机车车辆研究所， 北京 100081；2 北京纵横机电科技有限公司， 北京 100094)

车轮滑行保护(Wheel Slide Protection, 简称WSP)是制动系统的核心技术。当轮轨黏着较低时，WSP系统能有效抑制车轮滑行，不但能防止轮对擦伤和抱死，而且能最佳利用有效黏着，以保证最短的制动距离[1]。由于轮轨黏着特性的非线性、时变性和复杂性，难以建立精确的数学模型，实现理想化的防滑控制是相当困难的。因此，目前实际应用的防滑控制系统普遍以大量的试验数据积累为基础，进而得到优化的防滑控制参数和控制策略，同时配合高精度的传感器、高速的控制器等技术才能实现有效的防滑控制，这种方式成本高、周期长、管理难。基于上述原因，可将模糊逻辑控制器(Fuzzy Logic Controller，FLC)应用于WSP系统。模糊逻辑控制器具有控制复杂系统的优势，不需要精确的数学模型，模糊规则库可通过有效可信的测试数据(或者数学仿真结果)和专家知识相结合等方式获得。由于试验成本高、轮对擦伤风险等原因，获得实际列车测试数据是相当有限的。通常采用列车制动的仿真数据代替实测数据以用于模糊逻辑控制器的前期设计和优化，实际列车测试在控制器设计的最后阶段才进行，以验证所设计防滑控制器的有效性和可靠性。此外，有经验的专家可提供描述防滑控制系统的语言规则，这对于有限的测试数据是相当重要的，可以获得测试数据无法确定的控制规则[2-3]。

在深入分析黏着理论、防滑控制、模糊原理的基础上，结合前期制动系统的设计和开发经验，提出了一种基于模糊控制的防滑控制方法。通过专家知识和测试数据获得模糊控制规则库，并在实时仿真平台上进行了仿真测试和优化。仿真测试结果表明模糊防滑控制器不但能有效控制轮对滑行，避免轮对擦伤，而且能有效利用黏着，保证较短的制动距离，验证了模糊防滑控制器的有效性和可靠性。

1 黏着基本理论

列车制动时依赖轮轨间的黏着力，所以按照黏着特性来控制制动力是极为重要的。如果不进行适当的制动力控制，就会在黏着力低于制动力时发生滑行。然而，轮轨间的黏着系数却是一个复杂多变的参数，受列车制动控制系统设计、环境和运用条件等诸多因素的影响，它在自然条件下的随机变化虽有统计规律可循，可就任一时刻而言它是随机和不可预知的。因此要想最大限度地发挥制动功率，必须系统的了解轮轨黏着机理。

1.1 黏着

黏着力就是在轮轨间接触部分伴随着微小打滑所传递的力。当车轮沿轨道滚动时，仅在接触面出现纵向(切向)相对运动的情况下，才能施加制动力。所以，与车轮摩擦定律中的摩擦系数不同，把沿车纵向传递的制动力，或者说轮/轨间接触面上的切向移动力F与法向力Q之比定义(纵向)黏着系数μ，即[4]：

(1)

1.2 蠕滑与黏着的关系

一般采用Kalker曲线来表示黏着系数与蠕滑率的关系，如图1所示。该曲线有两个稳定工作区间，第一个稳定区在蠕滑率为0.5%～1.5%左右处黏着系数达到峰值产生，由于通过这个区的时间很短，并且难以检测与控制，故称之为假稳定区，真正的黏着利用与控制是在第2个稳定区, 蠕滑率为5%～20%左右。Kalker曲线是理论曲线，实际通过测量和统计得到的黏着系数曲线不包括假稳定区[5]。

具体表现为，当制动开始后，制动缸压力逐渐上升，制动力随之增大，车轮速度开始降低，车辆速度和车轮速度的差值也逐渐增大，蠕滑率和黏着系数增大。在蠕滑率到达最大黏着点之前，黏着系数随蠕滑率的增大成非线性增大，此时车轮转矩和制动力矩可认为是同步增长的，制动过程处于黏着曲线的稳定区域。但继续增大制动力矩，蠕滑率超过某一值时，黏着系数反而下降，车轮转矩随之减小，与制动力矩之差急剧增大，最终使车轮速度大幅度减小直至车轮抱死。所以，在正常情况下，制动力Fb不应大于黏着力Fa，即制动力受轮轨黏着的限制[6]。

Fb≤Fa

(2)

1.3 防滑控制

防滑控制是在制动力即将超过黏着力时，降低制动力，使车轮继续处于滚动(或滚滑)状态，避免车轮滑行。防滑控制系统是防止制动过程发生滑行，达到最佳利用黏着，确保行车安全的重要部件。防滑控制系统通过轮轴速度传感器检测出此时的速度差和减速度，然后把检测到的信号传输到防滑控制器，通过微处理器进行比较判断，发出防滑控制信号来降低制动缸压力，使滑行车轮对应的制动力快速降低。当滑行消失后，防滑控制器重新恢复车轮制动力实施制动。防滑系统判断出滑行以后，控制制动力的变化过程也很重要。在判断出滑行后，并不是简单地降低制动力，而应通过对制动缸压力反复进行减压、保压和升压，来最大限度地利用轮轨间黏着。所以防滑控制系统对制动力的控制既要能防止滑行，又要不致使制动力损失过大，以充分利用轮轨黏着[7-8]。防滑控制过程如图2所示。

图2 防滑控制原理

2 模糊防滑控制系统

目前，传统的防滑控制系统通常以大量的试验数据积累为基础，进而得到优化的防滑控制参数和控制策略，这种方式具有成本高、周期长、管理难的问题。从防滑控制的角度来说，一方面轮轨黏着特性具有较强的非线性、时变性和复杂性；另一方面，通过直观的专家知识可以实现滑行控制。基于上述原因，模糊逻辑控制广泛地应用在防滑控制中。采用模糊逻辑，非线性系统的语言描述可直接根据模糊IF-THEN规则库进行模型化。此外，由于模糊控制器允许采用测试数据和专家知识(语言规则)相结合的方式形成控制算法，因此在设计防滑控制器时采用模糊控制具有使用测试数据少、不依赖于精确模型的优点。

文中设计了一种基于模糊控制的防滑控制系统，其结构组成如图3所示。一个非接触型速度传感器装于车轴，其与车轮的速度成比例的脉冲信号传输到电子控制单元。电子控制单元对本车或本转向架的速度脉冲信号进行处理，得到各轴速度和减速度，然后模糊防滑控制器根据各轴的速度差和减速度进行滑行判断，对已经发生滑行的情况发出防滑控制指令，控制防滑排风阀，调整制动缸压力。模糊防滑控制系统能最佳利用有效黏着，以保证最短的制动距离。

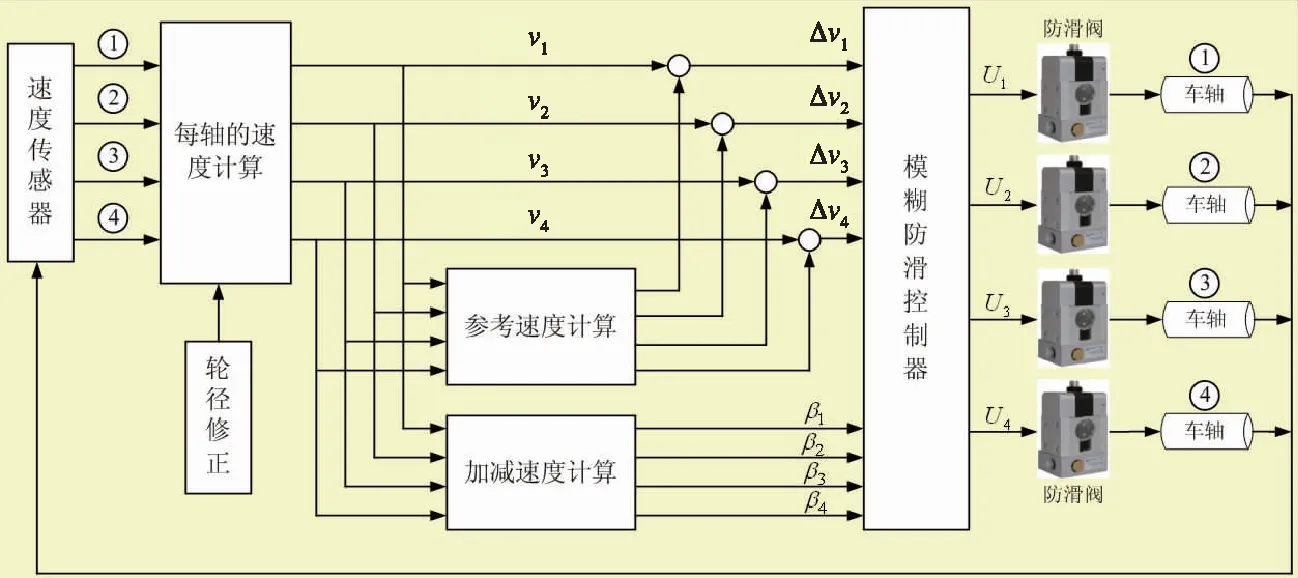
图3 模糊防滑控制系统结构

图3中的模糊防滑控制器主要由4个部分组成，包括模糊化、知识库、模糊推理和清晰化[9]，如图4所示。

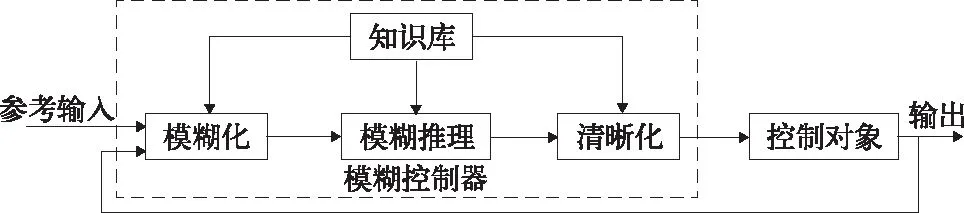
图4 模糊控制器结构

(1)模糊化

这部分的作用是将输入的精确量转换成模糊化量，具体过程如下：

① 首先对输入量进行处理变成模糊控制器要求的输入量；

② 将已经处理过的输入量进行尺度变换，使其变换到各自的论域范围；

③ 将已经变换到论域范围的输入量进行模糊处理，使原先精确的输入量变成模糊量，并用相应的模糊集合来表示。

(2)知识库

知识库中包含由数据库和模糊控制规则库两部分组成：

① 数据库包括变量的隶属度函数、尺度变换因子和模糊空间的分级数等；

② 规则库是一系列控制规则，反映了控制专家的经验和知识。

(3)模糊推理

模糊推理是模糊控制器的核心，用来模拟人的推理能力，该过程是基于模糊逻辑中的相互关系及推理规则来进行的。

(4)清晰化

清晰化的作用是将模糊推理得到的模糊控制量变换为实际控制量，包括两部分内容：

① 将模糊控制量经清晰化变换成论域范围的清晰量；

② 将表示在论域范围内的清晰量经尺度变换变成实际控制量。

3 模糊防滑控制器设计

文中所设计的模糊防滑控制器为双输入单输出结构，速度差Δv和减速度β作为输入，制动压力P作为输出，详细的模糊防滑控制器设计如下。

3.1 输入输出模糊论域划分

(1)输入量变换

(3)

其中，k为比例因子：

(4)

设定速度差Δv的论域范围为[0，5]，根据速度差实际输入量范围，量化等级为0, 1, 2, 3, 4, 5。减速度β的论域范围为[-4，3]，根据减速度实际输入量范围，量化等级为-4, -3, -2, -1, 1, 2, 3。

(2)输出量变换

输出量的变换方式与输入量的变换基本相同，设定输出制动压力 的论域范围为[-3，3]，量化等级为-3, -2, -1, 0, 1, 2, 3，但量化等级仅表示制动压力P的控制状态变化。

(3)输入输出空间的模糊分割

根据输入输出的量化等级，输入输出的空间模糊分割如下：

对应速度差 输入的量化等级0, 1, 2, 3, 4, 5，设定模糊分割空间为ZO、PSS、PS、PM、PB、PBB，分别表示零、正极小、正小、正中、正大、正极大。对应减速度 输入的量化等级-4, -3, -2, -1, 1, 2, 3，设定模糊分割空间为，NB、NM、NS、NSS、PS、PM、PB，分别表示负大、负中、负小、负极小、正小、正中、正大。

制动压力 输出的量化等级为-3, -2, -1, 0, 1, 2, 3，设定对应的模糊分割空间为NB、NM、NS、ZO、PS、PM、PB，分别表示制动压力 的控制状态变化，如表1。

表1 制动压力输出变化

表中：V1 阶段排风(小)；V2 阶段排风(大)；V3 全排风；H 保压；C1 阶段充风(小)；C2 阶段充风(大)；C3 全充风。

3.2 输入输出隶属度函数

设定速度差输入Δv、减速度输入β和制动压力输出P的隶属度函数都采用三角形隶属度函数，如图5。

图5 输入输出隶属度函数

3.3 模糊控制规则库

模糊控制规则是模糊控制的核心，一般由一系列“If-Then”型的模糊条件句所构成，条件句的前件为输入和状态，后件为控制变量，例如：

If Δvis ZO andβis NB，ThenPis NB

If Δvis ZO andβis NM，ThenPis PS

If Δvis PBB andβis PB，ThenPis NS

根据速度差输入模糊分割数为6和减速度输入模糊分割数为7，则模糊控制规则为维数6×7的矩阵，共有42条控制规则。基于专家知识获得的模糊控制规则矩阵如表2所示。图6是采用Matlab的Fuzzy模糊库得到的模糊控制规则三维模型。

表2 模糊控制规则矩阵

图6 模糊控制规则库Matlab三维模型

3.4 模糊推理及清晰化计算

根据模糊控制器的输入模糊量 和 以及表2中的模糊控制规则库进行近似推理，可以得出输出模糊量 。模糊推理过程中与运算采用求交(取小)的方法；合成运算采用最大—最小的方法；蕴含运算采用求交的方法，清晰值计算采用加权平均法。利用Matlab的Fuzzy模糊库，得到输出量 的控制表，如表3。

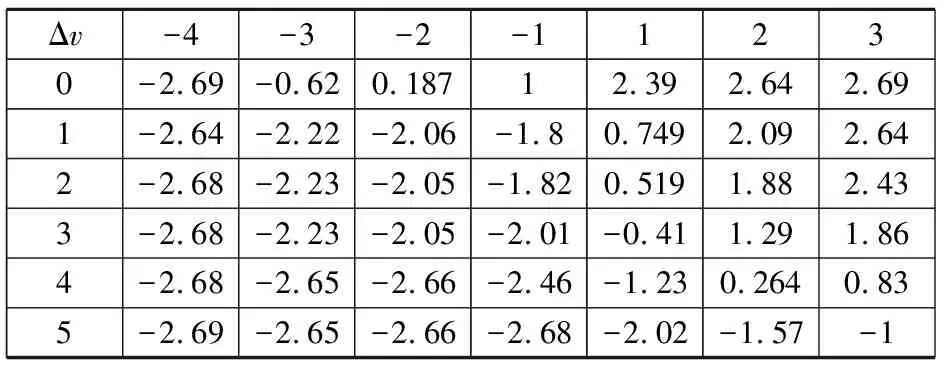
表3 输出量控制表

3.5 输出状态的确定

根据表1，将表3中的输出量P换算到模糊分割空间(表4)，并确定输出量P的控制状态(表5)。

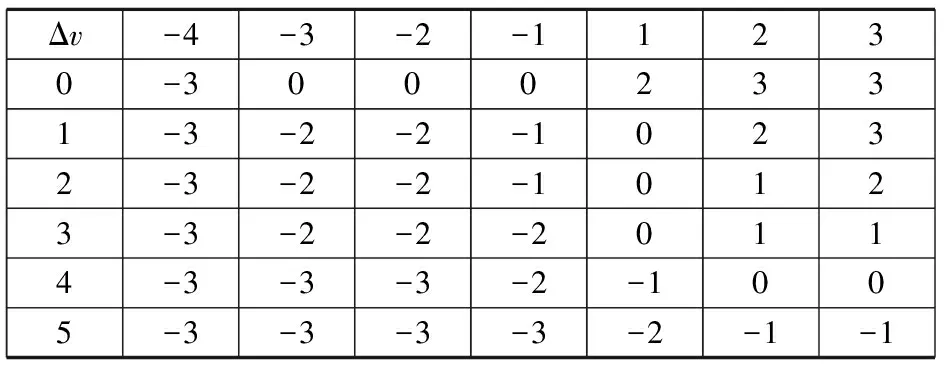
表4 输出量的模糊分割空间

表5 输出量的控制状态表

4 模糊防滑控制器的仿真测试及优化

为了验证文中设计的基于模糊控制的防滑控制器有效性和可靠性，在仿真测试平台上对其功能进行了测试，并根据实车防滑测试数据对模糊控制规则进行了优化。

4.1 仿真测试平台

采用专用开发工具建立了模糊防滑仿真模型，主要包括参数模块、速度模块和主控制器模块、黏着模块等。在实时硬件平台上对模糊防滑控制器进行了仿真测试。图7为模糊防滑仿真模型及实时硬件平台。

4.2 防滑仿真测试及优化

在实时硬件平台上，进行了基于专家知识库的模糊防滑仿真测试，其测试结果如图8所示。

从图8可以看出，虽然模糊防滑控制器能有效抑制轮对滑行，防止轮对抱死，但其黏着利用较差，延长了制动距离，因此需要对模糊控制规则进行优化。可采用现车测试数据对模糊控制规则库中较差的模糊控制规则进行优化。现车测试数据是基于传统设计的防滑控制器而获得的，一般包括轴速、轴减速度、制动缸压力等，如图9。由于一些现车防滑测试数据并不适合作为训练样本(例如，防滑控制效果较差)，因此只采用防滑控制效果较好的现车测试数据(例如，既能有效抑制轮对滑行又能充分利用黏着)作为训练模糊控制规则的样本。经100组以上样本训练优化后的模糊控制器输出量控制状态如表6。优化后的模糊控制器防滑仿真测试结果如图10所示。

图7 模糊防滑仿真模型及 ES1000硬件平台

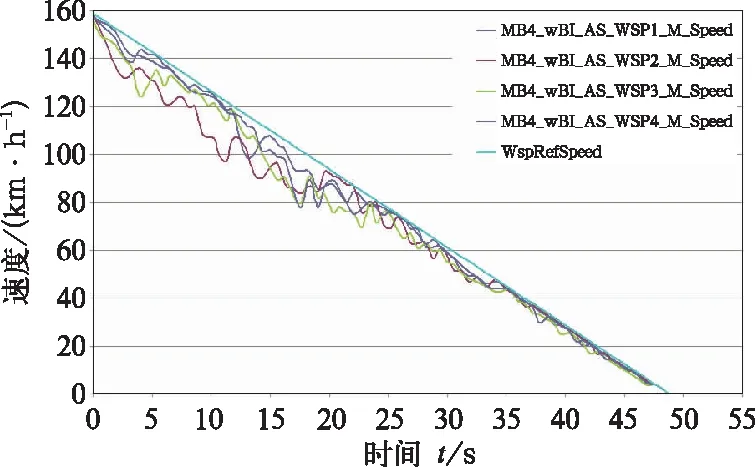
图8 基于专家知识库的模糊防滑仿真测试

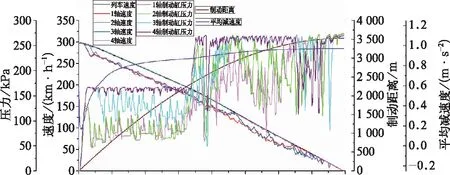
图9 基于传统防滑控制器的现车防滑试验数据

Δv-4-3-2-11230全排保压保压保压阶充快全充全充1全排阶排慢阶排慢保压阶充慢阶充快全充2全排阶排快阶排慢保压保压阶充慢阶充快3全排阶排快阶排快阶排慢保压阶充慢阶充慢4全排全排全排阶排快阶排慢保压保压5全排全排全排全排阶排快阶排慢阶排慢

图10 优化后的模糊防滑控制器仿真测试

从图10可以看出，优化后的模糊防滑控制器具有好的控制性能，不但能有效抑制轮对滑行又能充分利用黏着，缩短了制动距离。

5 结 论

在深入分析黏着理论、防滑控制、模糊原理的基础上，结合前期高速动车组防滑控制系统的设计和开发经验，设计了一种基于模糊控制的防滑控制方法。模糊控制规则采用专家知识和实际试验数据相结合的方式获得，并在实时仿真平台上对模糊控制器进行了仿真测试。仿真测试结果表明模糊控制器能有效抑制轮对滑行，并能最佳利用黏着，缩短制动距离，验证了模糊防滑控制器的有效性和可靠性。与传统的防滑控制器相比，模糊防滑控制器具有设计简单、性能高、成本低、周期短等优点。下一阶段的工作就是将模糊防滑控制器应用于实际轨道车辆，并进行线路试验验证，为今后模糊防滑控制器的工程应用推广奠定基础理论基础和技术支持。