基于量子Fisher信息的量子计量进展*

任志红 李岩 李艳娜 李卫东

(山西大学,理论物理研究所,量子光学与光量子器件国家重点实验室,极端光学协同创新中心,太原 030006）

量子计量是超冷原子气体研究中的一个热点领域.超冷原子体系独特的量子性质(量子纠缠)和量子效应有助于大幅度提高待测物理量的测量精度,这已经成为量子精密测量中的共识.量子Fisher信息对该领域的发展起了非常重要的作用.本文首先介绍量子Fisher信息的基本概念和量子计量的主要内容;然后简要回顾这些理论在提高测量精度方面的应用,特别是多粒子量子纠缠态的产生及其判定;再介绍线性和非线性原子干涉仪的相关进展;最后论述量子测量过程中的统计方法的研究进展.

1 量子计量简介

量子计量研究如何利用量子属性、量子效应来提高物理量的测量精度,以期突破散粒噪声极限 (shot noise limit,SNL)(或者标准量子极限(standard quantum limit,SQL)),趋近海森伯极限 (Heisenberg limit,HL).大多数需要精密测量的物理量(如电磁场场强、微弱惯性力以及时间频率标准等)都能被投影到相位上,而这些相位可以利用干涉仪进行推断估计.因此,干涉仪的设计是量子计量中的核心内容之一.由于没有与相位对应的厄米算符,因此其不能直接被实验测量,只能通过估计的方法获取.因此,相位估计 (phase estimation)就成为精密测量(量子计量)中的一个重要内容.一个完整的相位估计过程(如:引力波测量、原子钟以及重力测量仪等)一般由如下几部分组成:N粒子探测态制备、相位累积、可测物理量(M)的测量以及相位估计(如图1所示).换言之,量子计量的目的就是研究如何在探测粒子数给定、相互作用(相位累积)时间有限的前提下,尽可能获得精确 (小涨落) 的参数估计.噪声 (noise)是决定大小的重要因素,通常可分为经典噪声和量子噪声[1].一般地讲,经典噪声是非本质的,总是可以被克服(或抑制),而量子噪声由量子力学的基本原理决定[2],是本质的、不可克服的.目前双模式的原子干涉仪的√测量精度已经接近标准量子极限,即,其中是探测态中非关联的粒子数[3].标准量子极限来源于测量的统计属性,是中心极限定理的直接结论[4,5].早期的理论研究表明,标准量子极限是可以被突破的[6−8].利用超冷原子系统的量子特性,实验上已经在突破标准量子极限的方向上取得了显著的进展(见图2）.如何在有限的量子资源下突破标准量子极限、趋近海森伯极限是量子计量学研究的核心问题之一[9−21].

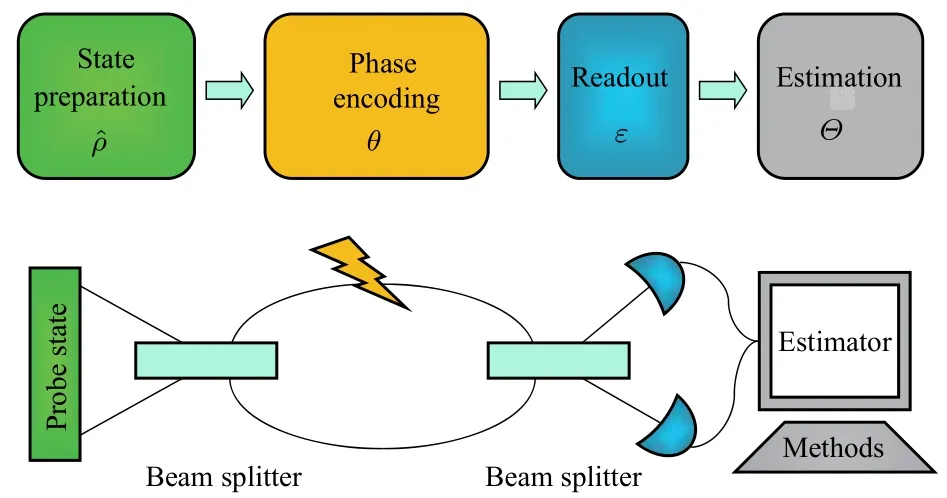
图1 相位估计的流程示意图 (1）探测量子初态 的制备;(2） 待测相位 的编码,量子初态演化为 ;(3）正定的测量算符(POVM)对末态进行测量;(4）待测相位的统计估计 .图的下部分是马赫曾德 (Mach-Zehnder,MZ)干涉仪的应用实例.图取自文献[4]Fig.1.Here we schematically plot the elements of complete phase estimation:(1）the preparation of prob state ;(2） the encoding of phase shift ,which transform the probe state to ;(3）the readout measurement of the POVM and finally(4）the mapping from the measurement results to the phase provided by the estimator .The phase sensitivity crucially depends on all these operations.The lower panel shows the application to Mach-Zehnder interferometry.Adapted from Ref.[4].

基于量子力学原理的物质波干涉仪的发明是量子计量中的一个重要进展.继电子、中子干涉仪之后,原子干涉仪也已经发展了20多年.特别是随着对超冷原子的操控与测量技术的进步,原子干涉仪在近十年来有了非常快速的发展[22].目前原子干涉仪在重力[23−26]、惯性力[27−34]等方面的测量已经达到了很高的精度.国内的相关进展,可参见近期《物理学报》关于“精密测量的专题”[35].

利用原子的内部能级作为双模干涉仪的模式,通过Ramsey干涉仪技术[36]对原子跃迁频率的测量是近代原子钟频率基准的核心技术之一[37,38].超冷原子系统不仅在推动精密测量方面具有非常重要的意义,而且对深入理解量子力学的基本问题(比如:量子力学非定域性、量子纠缠等)也有重要的促进作用[39](某种意义上也促进了对量子理论基本问题的进一步思考,比如:量子力学诠释问题的重新讨论[39]).传统的量子计量存在一些缺点：一方面,量子计量原则上要求多粒子(通常成百上千)组成的量子态作为探测态,但是对这些粒子同时进行单独测量是非常困难的;另一方面,多粒子量子态重构所要求的独立测量次数呈指数形式增加,这也是一个难以克服的困难.因此,需要发展一种全新的、基于有限次测量的多粒子量子纠缠态刻画的理论方法.目前,对多粒子量子体系的操作(或测量)基本上都是同时的集体(collective)操作(或测量),新方法需能够从集体操作过程中汲取多粒子量子关联态的信息.

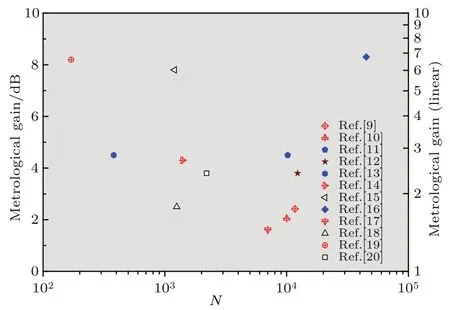
图2 近年来利用超冷原子体系取得的超越标准量子极限的实验进展.对数增益 (左): 和对应的线性增益 (右): ,其中 或者 为 自 旋 压 缩 参 数 , 为 量 子 Fisher 信息.空心图标为净增益,即去除测量误差的增益;实心图标为可能增益，即实验纠缠态的可能增益;十字交叉图标为干涉仪增益，即通过干涉仪验证的增益. 为实验中所用的总粒子数目(或平均数目).图取自文献[5]Fig.2.Gain of phase sensitivity over the standard quantum limit achieved form recent Bose-Einstein condensates experiments.The logarithmic gain is shown in left, and the linear gain is in right,The measured phase precision is obtained by spin-squeezing parameter ,i.e., ,or from ,i.e., .Open patterns are inferred values,being obtained after subtraction of detection noise;Filled patterns report witnesses of metrologically useful entanglement measured on experimentally generated states,representing potential improvement in sensitivity;Cross patterns show the measured phase sensitivity gain obtained from a full interferometer sequence.Here is the total number of particles (or mean total)used in experiments.Adapted from Ref.[5].

近年来,基于量子Fisher信息的基本概念,我们小组以冷原子系统为对象,较为系统地开展了量子计量相关的研究工作.本文以时间频率测量为主线,简要回顾量子计量的历史进程;介绍基于量子Fisher信息的量子计量的主要内容;阐述在此基础上发展的多粒子量子纠缠态的产生及其判据;简析新型原子干涉仪工作原理以及相位估计过程中新的、可控量子过程的设计思路.

1.1 历史回顾

早在 1873 年,Maxwell(麦克斯韦)[40]就提议将波长为长度单位的光波的振动周期作为时间单位.但是当时的技术水平无法测量如此短的时间周期.一直到1937年,一系列新发明和技术进步(如:O.Stern改进了分子束控制技术和Stern-Gerlach实验[41])才使得原子内部能级的跃迁频率作为时间标准成为可能[37].同年,Rabi(拉比)[42]首次观测到中性分子的磁共振效应,并建议利用这种效应发展时间频率标准.1939年,实验上首次观测到了分子内部能级磁共振现象[41].这些工作为后来原子束磁共振频率钟的研究奠定了基础[37].1945年,第一台原子钟研制成功,尽管其精度不如同时期的机械(Mechanical)钟和石英(Quartz)钟,但是由于原子内部能级具有稳定性和一致性,所以对原子钟的研究并未停止.随着1949年Ramsey干涉仪原理的揭示[36],实现原子钟道路上的最后一个科学堡垒终于被攻克了.1967年,对铯-133原子的基态超精细能级(钟能级)跃迁频率的测量已经可以精确到约,较机械钟和石英钟的提高了近个数量级.因此,铯-133原子钟的跃迁周期被重新定义为秒的国际单位[43],这真正意义上完成了利用量子系统(或量子效应)实现时间标准的设想.从一定意义上讲,对频率(时间)测量精度的不断追求推动了量子计量的发展[44],时间测量精度提高的进程与量子计量发展的过程密不可分.目前所有的可测物理量中,时间测量的精度最高[43].事实上,得益于时间测量的超高精确度,对相关物理量的测量(长度、速度以及电压等)也可以达到非常高的精度.

关于量子计量的综述文献有很多[4,36,37],下面简要回顾量子计量理论发展过程中几个里程碑式的重要进展:1981 年,Caves[45]指出在光学 Michelson-Morley干涉仪的闭置端输入压缩真空态可以突破标准量子极限;随后的二十年里,人们逐步认识到将探测的量子态改为具有一定量子关联的非经典态可以大幅增加测量的精度,突破散粒噪声(标准量子)极限[4,7,46].近些年的研究[3]表明突破标准量子极限需要将探测态改为量子纠缠态.然而,并非所有的量子纠缠态都对提高量子计量的测量精度有益,只有那些可以被量子Fisher信息识别、对量子计量有用的多粒子量子纠缠态才可以真正地增强量子测量的测量精度[5,47,48].因此,如何甄别和利用量子态(特别是多粒子量子纠缠态的量子属性[5]和其他量子效应[49])来提高量子测量的测量精度,成为了量子计量的重要研究内容.本文将针对这些内容进行介绍.需要指出的是,量子Fisher信息作为甄别幺正操作下量子态纠缠特性的重要基本概念,在量子相变等其他热点问题中也有广泛的应用[50−59],但这部分内容不在本文的讨论范围之内.

如前所述,本文主要以量子干涉仪为模型进行讨论.一方面,物理学的进步某种程度上得益于人们对物理量的精密测量,而量子纠缠态是进一步提高测量精度并且研发下一代高灵敏探测仪器的关键;另一方面,量子干涉仪是研究量子力学基本问题的重要模型之一.

1.2 相关的基本概念

统计估计的精度到底是多少？是否存在一个基本的极限？这是统计推断(statistical inference)中的核心问题之一.早在20世纪40年代,Rao[60],Cramér[61]以及 Fréchet[62]就分别独立证明了对于单变量的统计估计存在一个最低的极限(随后由Darmois[63]将上述结果推广到多变量情况).这个极限就是 Cramer-Rao下界 (Cramer-Rao lower bound,CRB),其与 Fisher[64]早些年提出的 Fisher信息有直接关系(在相位估计理论中,还存在许多其他极限.特别是在有限测量次数时,有些比CRB更为严格,本文将在第四部分简单介绍).因此,Fisher信息是相位估计理论中的核心概念.考虑所有可能的量子测量条件,Fisher信息的最大值被称为量子Fisher信息[1,65].相应地可定义量子Cramer-Rao 下 界 (quantum Cramer-Rao lower bound,QCRB)[2,66,67].

本节首先对Fisher信息和量子Fisher信息的定义、基本性质以及与此相关的相位估计理论进行简单的介绍.关于Fisher信息和量子Fisher信息的相关综述可以参阅文献[68,69].在介绍和证明QCRB之前,先介绍似然(likelihood)函数和估计子.

1）似然函数和估计子.如图 1 所示,一个完整的相位估计单元包括:初始的探测态的制备;一种可参数 (实数)化的、对探测态的操作 (如:干涉仪的转动操作,参见第三部分内容);利用末态(输出态)获得可测物理量的测量值 ();对待测参数的估计(通过对多次测量结果的统计分析而获得).这里的测量结果既可以是分离变量(如MZ干涉仪中的粒子数),也可以是连续变量(如双缝干涉仪中的干涉条纹).一般地,量子测量用一个正定的测量算符(positive-operator valued measure,POVM)表示(测量理论中的算符在一定程度上具有测度的意义,因为它不只是一个力学量,同时还将概率算符与测度相联系.因此,严格地说此算符为测度算符).POVM算符是一个厄米算符,需满足两个基本要求:1）概率测量值非负;2）.给定时,获得测量值为的条件概率分布函数(亦被称为似然函数)定义为

1.3 Fisher信息和Cramer-Rao lower bound (CRB)

CRB是相位估计理论中一个非常重要的概念,其受中心极限定理的保证.对于任意的估计子而言,其涨落 ((7）式)存在如下极限

其中求和是对所有可能的测量值进行求和.(9）式是CRB的一般表达式.对于无偏差估计而言,即,CRB表明测量的涨落与Fisher信息成反比.CRB可以通过考虑涨落的定义(7）式、似然函数的归一化条件和柯西-施瓦茨(Cauchy-Schwartz)不等式来证明,详细过程参见附录A1.

由附录A1的推导可知,有效估计需要满足

1.4 量子Fisher信息与量子CRB

1）量子 Fisher信息.对所有可能的 POVMs而言,Fisher信息((10)式)的最大值就定义为量子Fisher信息[1](本文将视情况使用不同的记号:如果只是计算Fisher信息,由于对所有测量值进行了求和,此时 Fisher将只是参数的函数,记为;而由于概率分布函数或是条件概率函数也与末态以及 POVMs相关,强调这些关系

量子Fisher信息的最大值((13）式)与具体的测量算符并无明显的依赖关系.对于所有可能的POVMs而言,至少存在一个POVM同时满足条件(16）式和(17）式,使得Fisher信息取最大值.如果是可逆的,对所有的而言,两条件可以等(17）式成立的充分但不必要条件.如果考虑是厄米算符,则存在一组完备的量子态,使得,其中是实数.如果选取由组成的 POVM,显然当时条件 (17） 式成立,同时为实数,即(16）式也成立.这就证明了至少存在一个可以用的正交归一基底组成的POVM,可以使Fisher信息取到最大值,即量子 Fisher信息.如(15）式所示,即使对最优化的 POVM,Fisher信息和量子 Fisher 信息一样,都是与相关的.这在某种程度上产生了矛盾,因为要找到一个优化的POVM使Fisher信息取最大,需要事先知道未知参量的准确值,这看起来是不可能的.但是,文献[70]表明,可以利用一种渐近的方法来克服这个困难.最近的研究[71]也表明,在一定条件下,最优测量是不依赖于待测参数的.

这个性质((20)式)表明,将量子态进行线性混合并不能增加已获得的测量精度.

相应的CRB((9）式)可以写为

对于非满秩的密度矩阵,(29）式存在奇点,将造成求解的困难.此时,量子Fisher信息仍存在严格的求解方法[73−75].对称对数导数在量子Fisher信息的计算中起重要的作用,因而对称对数导数的本征态又与最优测量有密切的关系[76].

需要指出的是,纯态的量子Fisher信息(31）式还可以利用在探测初态与其垂直空间的投影测量,在下,渐近地得到.具体证明见文献 [4].

6）幺正演化下的量子Fisher信息.考虑如下的幺正演化算符:

8）最大似然估计子.最大似然估计子(maximum likelihood estimator,MLE)是指与测量值相关的似然分布函数的最大值所对应的相位值:].当测量的次数趋于无穷时,最大似然算子的估计值满足以真实值为中心的高斯分布,且其方差为Fisher信息的倒数:

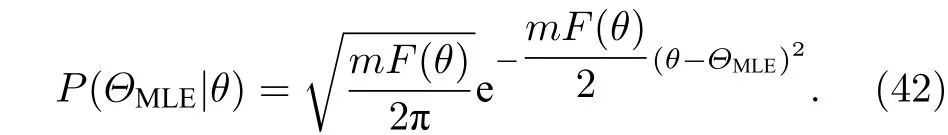
因此,最大似然估计子是渐近无偏的,它的方差总是可以达到 CRB,.中心极限定理保证了最大似然估计子比其他的估计子都要好.

正如文献[47]所表明的,通常情况下(43）式并不是最佳的,即,即使在中心极限定理条件下,也不一定可以达到CRB.只有当统计分布函数为高斯型时,

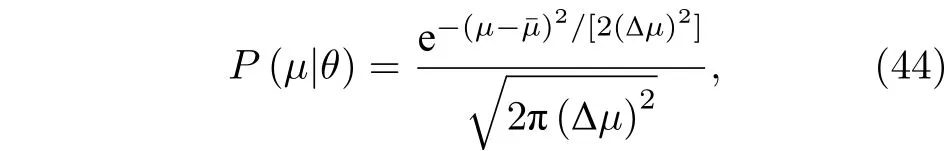
2 多粒子量子纠缠态的制备与判别

利用量子Fisher信息与待测物理量测量精度的关系,基于量子Fisher信息的多粒子量子纠缠判据已经得到了广泛的应用,比如连续变量的纠缠判定[82].本节首先解释为何多粒子量子纠缠态可以提高量子计量的测量精度.在上节介绍的量子Fisher信息基本概念的基础上,给出一个关于多粒子(分离变量)量子纠缠态的判据,进而给出对提高量子计算精度有用的多粒子量子纠缠态的定义.利用条件概率分布函数,介绍一种可以直接从实验数据中提取Fisher信息的方法;利用实验结果对所提出的方法进行验证.最后,介绍一种利用光与原子相互作用产生不同自由度量子纠缠的新方案.

2.1 统计距离与相位精度

被映射在量子态中的参数估计(或是相位估计)问题,在很大程度上等价于如何有效区分参数空间中相邻量子态的能力[1,83].因此,从这个角度来讲,干涉仪的相位估计精度可以认为是其对可能的最小相位差导致的输出量子态与初始探测态的分辨能力.这个性质可以通过定义在统计空间中的量子态的统计距离(statistical distance)来描述[84]

(47）式表明,Fisher信息可以理解为某种统计速度或者在最优测量条件下写为.它反映了统计分布函数在(或者)时随参数变化的某种速率.必须指出的是,在所有分析量子测量极限的问题中,条件概率分布函数是一个共同的出发点[85].实验上,固定待测参数(),对测量量子态进行多次测量,原则上可以得到在给定参数条件下测量值空间中的分布函数,如图3所示.对待测参数进行改动,重复之前的测量过程,可以得到以为参考点的邻近条件统计分布函数.因此,原则上 (47）式提供了一种直接从实验数据中获取Fisher信息的方法[13,84].显而易见,(45）式和(46）式与具体的测量方式相关,因此会有不同的统计距离定义.比如,也可利用信息论中描述两个邻近统计分布关系的物理量[86]来表示,即 Kullback-Leibler(KL)熵

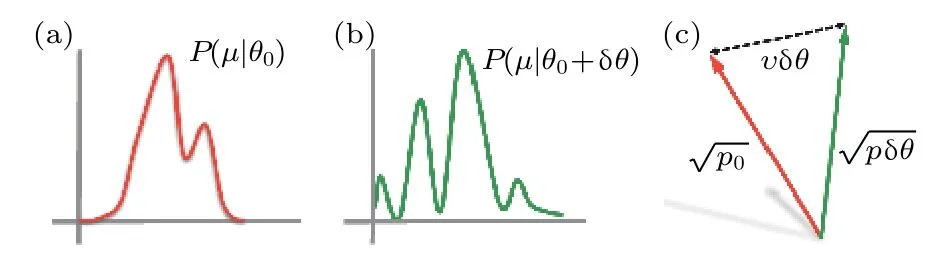
图3 统计区分度和统计速度的示意图.在给定 的条件下,分析测量数据可得分布函数 (图(a)红线)和调节 后 得 分 布 函 数 (图 (b) 绿 线 ).图(c) 示 意 由 和 定义的态矢量及其欧几里得距离(统计距离),其 中 是 衡 量 统 计 区 分 度 的统计速度.图取自文献[84]Fig.3.Here we give the sketch of statistical distinguishability and statistical speed. The probability distribution is obtained by collecting the measurement results for different values of the parameter,here chosen to be (red line)(a)and(green line)(b). (c) to quantify the statistical distinguishability between the two distributions we introduce unit vectors (red)and(green), then we obtain the Euclidean distance between them: .Here the denotes the statistical speed.Adapted from Ref.[84].

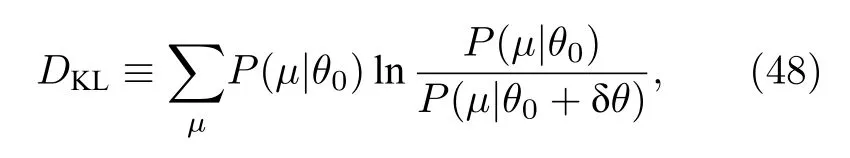
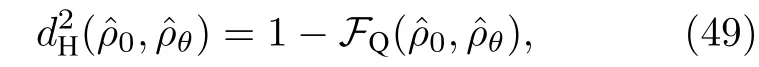
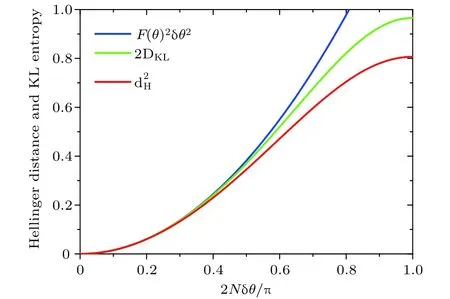
图4 海林格距离 (红线) 和 KL 熵 (绿线),以及他们共同的二阶展开项 (蓝线)的比较.图取自文献[84]Fig.4.Hellinger distance, (red line),KL entropy,(green line),and their common low-order approximation,(blue line),as a function of .Adapted from Ref.[84].

利用统计距离从实验中读取量子Fisher信息囚禁的离子体系,由于其与周围环境很好地隔离,可以成功地实现诸如相干控制、独立寻址和高效率量子态测量等操作,是成功产生与探索多粒子纠缠态的重要系统之一.由于篇幅所限,这里不作详细介绍,有兴趣的可以参考文献[5,89,90].这里采用6个[91]和14个[92]离子的最大纠缠态(薛定谔猫态)

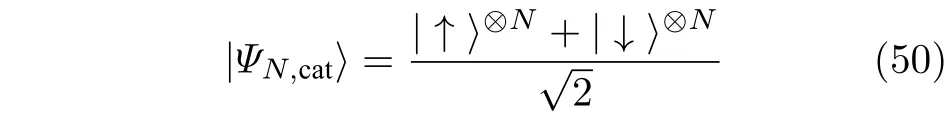
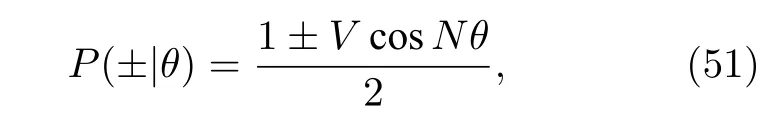
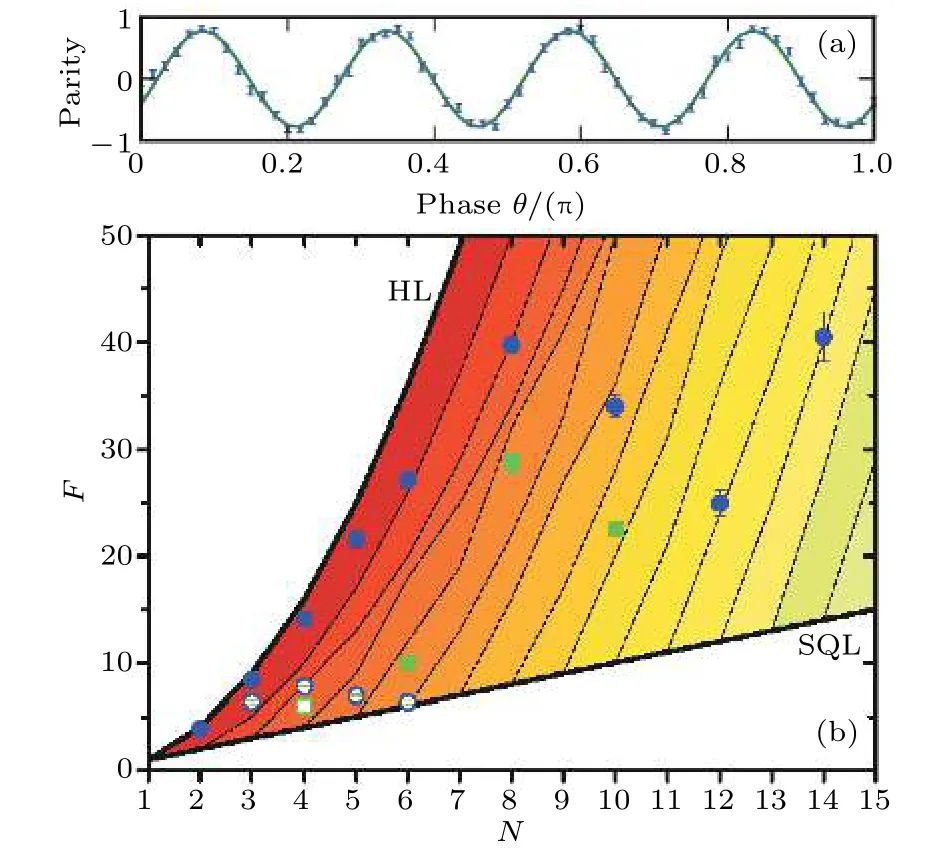
图5 宇称振荡的测量结果和提取的 Fisher信息 (a)GHZ( )的宇称测量图,周期为 ,取自文献[92];(b)基于近期实验结果得到的Fisher信息与总粒子数 的关系 ,其中 为实验中的对比度.上边界粗线为海森堡极限,即 ,下边界黑色粗线代表标准量子极限, .图中其他的细线分别表示 粒子纠缠的边界,即方程 (60).其中 的圆圈表明 粒子纠缠.图取自文献[84]Fig.5.Experimental results based on parity measurement and extracted Fisher information： (a) Typical parity oscillations obtained with cat states.The period is .Adapted from [92]; (b) summary of the experimental achievements,ions(circle)and photons(square).Here we show the Fisher information as a function of the number of qubits , , obtained from the extracted experimental visibilities .The upper thick line is the Heisenberg limit , the lower thick line is the standard quantum limit, .The different lines are bounds for useful -particle entanglement,Eq.(60).For instance, the filled circle at reveals useful -particle entanglement.Adapted from Ref.[84].

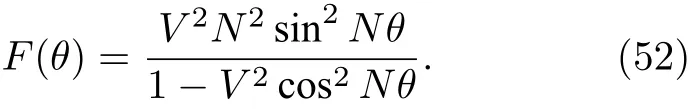
2.2 量子纠缠与相位精度

该极限与测量的估计子、测量方法等无关,但是受限于对系统中各粒子的局域操作.有意思的是,(58）式中测量次数与探测态中粒子数有相似的作用,只使用一个粒子作为探测态重复次相同的测量,与使用具有个粒子作为探测态测量一次有着相同的测量精度.这实际上是另一种与量子纠缠无关的量子增强测量理论的核心理念[49].

3）有 用 的 量 子 纠 缠 态 .如 果 某 量 子 态在(68）式描述的操作下所得到的量子Fisher信息不满足 (57）式,也就是说

则表明该量子态具有多粒子量子纠缠特性,因此,(59）式是量子态是多粒子量子纠缠的充分条件.更准确地讲,(59）式可以作为判定有利于量子计量精度提高的量子纠缠态的一个充分必要条件:对于一个满足条件(59）的量子态而言,如果利用它作为探测态对某个小的相位进行估计,假定该相位通过某种干涉仪的相互作用((68）式)引入,所能得到的测量精度将超过标准量子极限(58）式.这也意味着,并非所有的量子纠缠态都对提高测量精度或是超越标准量子极限有用[47].而对测量精度提高不大的多粒子量子纠缠态可能有助于其他量子技术.实际上,量子技术依赖于对量子态的测量,即依赖于对量子态自由度的操控.同时,即使是对测量有用的量子纠缠态,对测量精度的提高也不尽相同:具有较大量子Fisher信息的量子态,同时也具有更深的纠缠深度.对于组份的纠缠态((56）式),其量子Fisher信息满足如下不等式[100]

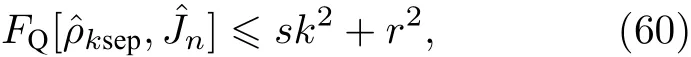
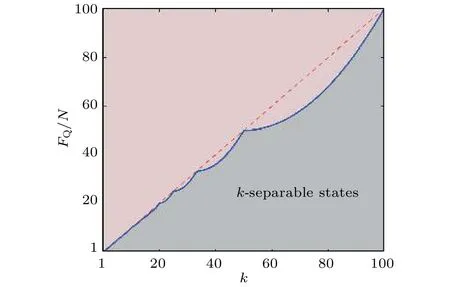
图6 有利于量子计量的 粒子纠缠判据.图中蓝色的实线由方程 (60)给出: 粒子纠缠态的量子 Fisher 信息.虚线为 ,其中粒子数 .该图取自文献[100]Fig.6.Useful -particle entanglement for quantum metrology. -separable states have a quantum Fisher information bounded by the solid line,Eq.(60).The dashed line is .Here .Adapted from Ref.[100].

因此,(61）式确定了由量子理论决定的相位测量的新极限[3],称之为海森堡极限 (Heisenger limit,HL)(海森伯极限最早在1993年由Holland和Burnett[105]引入,纪念海森伯不确定关系,将它用在粒子数与相位的测不准关系中.这里所说的海森伯极限特指)(也可以将输入干涉仪的粒子数与独立测量的次数一起进行优化[85,106,107].这样可将海森伯极限写为,其中,是在给定测量粒子数时,使测量精度最大的最优测量次数.由于该测量次数可能与测量态粒子数相关,因此,尽管可能测量态的Fisher较大,但其测度精度较标准极限好).不难看出√,(58） 式与 (62） 式对的依赖关系不同,相差倍,并且这个差别是不可能通过经典关联(或是可分的)态来克服的.但需要注意的是,克服标准量子极限(58）式还可采用Multi-round的方法[3,5].

3）多粒子纠缠判据与量子Fisher信息.自旋压缩态是指一类量子态,它在沿某一给定方向上的自旋测量值的涨落较小,同时,在垂直方向上的自旋测量值具有较大的涨落,但是,两者的乘积满足海森堡测不准关系.自旋压缩态是一类已经被证明在突破标准量子极限方面非常有用的量子纠缠态.通常用Wineland等[7,46]在1992年左右提出的自旋压缩因子

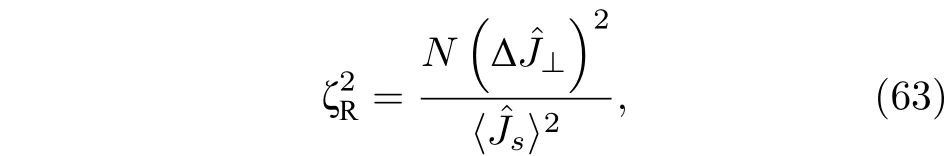
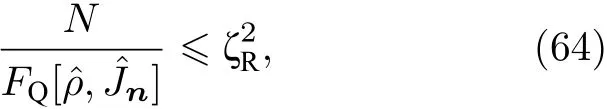
利用直接从实验数据中获得的量子Fisher信息值,以及关于有利于量子计量的组份的多粒子量子纠缠判据(60)式,我们得到了图5.图中黑色的圆点为从实验中获得的宇称性测量结果的量子Fisher信息值[92].依据我们的计算,这个实验结果声称得到了14个离子的多粒子纠缠态,从量子Fisher信息的多粒子纠缠判据的角度来看,它大约得到了6个离子的纠缠态.有意思的是,随后实验小组利用Bell测量判据给出了新的判断,表明他们也只得到了与我们结果相同的6离子纠缠态[108].利用(52）式可以看到,粒子量子纠缠态的量子Fisher信息识别,对测量值的对比度也有要求,即

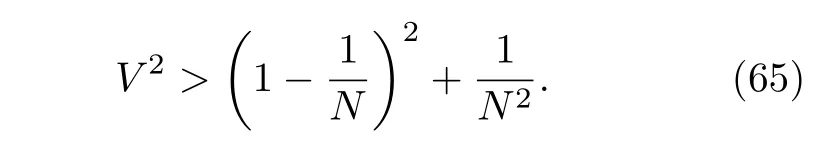
这就在一定程度上表明,退相干因素也是提高量子测量精度需要克服的因素.最后需指出,有一些具有纠缠性质的量子态(比如态),不能利用线性操作下的量子Fisher信息进行识别[5].

2.3 多原子量子纠缠态的制备

如前所述,多粒子量子纠缠态是进一步提高量子测量精度,甚至是关乎所有量子新技术的关键.因此,如何有效地产生多粒子量子纠缠态是目前量子物理中的一个关键问题和技术.由于粒子之间的纠缠,本质上是粒子的量子态(某种意义上是标记量子态的自由度的量子数,或者好量子数的某种纠缠,亦或可理解为是一些自由度之间的纠缠)之间的纠缠,因此,控制粒子的量子态(或自由度)之间的相互作用是有效产生多粒子量子纠缠态的核心要素.光学晶体中的光学非线性相互作用,即自发参 量 下 转 换 (spontaneous parametric downconversion,SPDC)方法,是实现纠缠光子对 (实现对偏振或模式的控制)以及压缩光场的重要手段,其中光子双数态以及连续变量的压缩光都是已经被证明的、有利于量子计量的量子纠缠资源.图2表明冷原子物理必将是一种在量子计量及量子信息中起重要作用的新量子资源(作为与光子完全不一样的量子体系正在引起人们的注意:1）静止质量;2）与外环境隔离比较彻底;3）可控的自由度高;4）已经在一些重要的测量方面取得相当大的成绩,如时间标准、重力测量等).超冷原子体系中可控的原子间弹性碰撞相互作用、囚禁外势是在其内态或是空间模式间产生量子纠缠的重要手段[5],比如:玻色约瑟夫森结的纠缠基态[20]以及非自旋压缩的量子纠缠态[13]等;超冷原子体系中的自旋相互作用是产生超冷原子对或是大量原子之间量子纠缠的重要手段(原子的双数态[9,109]和自旋压缩态[17,19]等);原子与光场的相互作用也可产生非定域原子之间的量子纠缠关联;利用里德堡原子偶极-偶极相互作用产生异核原子量子纠缠[110]等.另外,在离子体系中,静电相互作用和离子与光场的相互作用也是目前多离子体系产生多粒子量子纠缠态的有效方法[92],相关的综述可见文献[111−115].

1）原子双数态与量子相变.在大多数的原子体系中,多原子量子纠缠态的产生依赖于系统的动力学特性,即:通过初态制备并严格控制动力学演化时间来得到所需的多粒子(原子)纠缠态.近年来,考虑超冷原子系统的多体量子能谱特征,可以通过系统参数的绝热调节,实现系统在不同量子基态的转变(即量子相变)进而实现多粒子量子纠缠态的制备(明显的优点:1）产生可预知确切的量子态;2）一种全新的纠缠态制备方法).以自旋为的超冷自旋原子气体为例,相应的哈密顿量[116,117]可写为

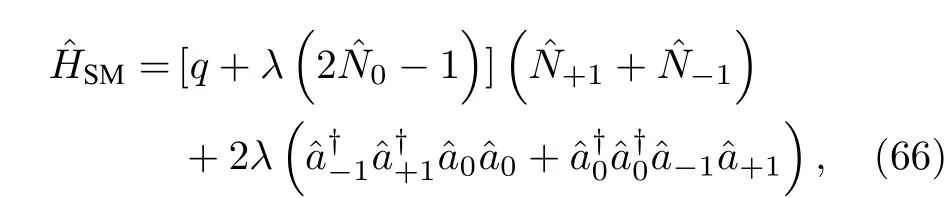
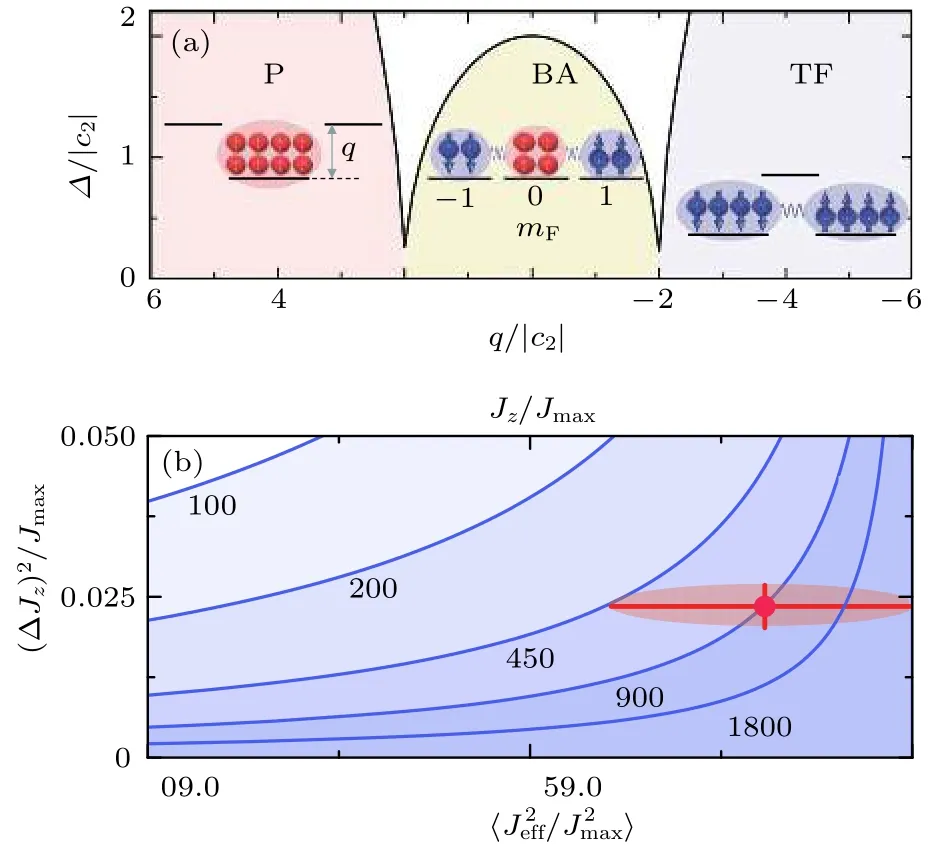
图7 (a)量子相变产生双数态过程;(b)纠缠宽度分析表明双数态纠缠宽度约为 原子.图取自文献[109]Fig.7.(a)Generation of twin-Fock state by quantum phase transition;(b) analysis of entanglement breadth for the Twin-Fock state samples,and it shows the entanglement breadth is at least atoms.Adapted from Ref.[109].

2）不同自由度的非定域特性.原子系统中多粒子量子纠缠态的研究不仅局限于多粒子量子纠缠态的产生,而且在理解诸如Einstein-Podolsky-Rosen(EPR)关联或是Bell非定域性方面也有重要的意义[5].Bell不等式是甄别粒子间关联特性的重要判据,不满足其要求的量子态之间的关联被称为最强量子关联[121].量子体系中这种非定域的关联特性是发展量子信息和量子计量等量子新技术的核心要素.相同自由度之间的量子纠缠或者非定域特性是一个被研究了很长时间的问题,特别是在光子体系中取得了非常大的进步.近年来,由于不同自由度之间的量子纠缠(非定域)特性在量子信息等领域中的重要作用,比如增加通讯的容量或增强量子通讯能力等,引起了人们的广泛注意[122].有意思的是,寻求不同自由度之间的相互作用不仅是量子计量,而且也是凝聚态物理中的重要课题.这在一定程度上促进了超冷原子体系中的另一个研究热点,人造量子规范势相关问题的量子模拟[123,124].因此,产生不同自由度量子态的量子纠缠的关键是要寻找连续自由度(动量)和分离自由度(自旋)之间的相互作用.

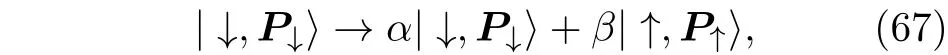
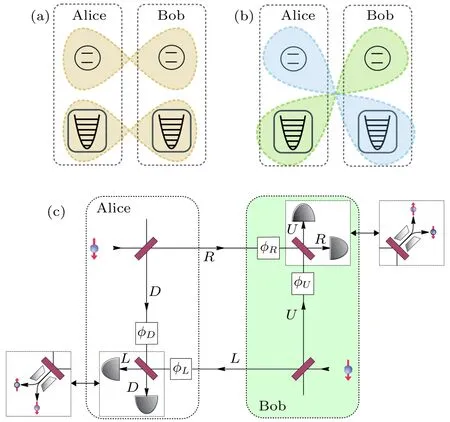
图8 两空间分离的粒子的相同自由度(a)和不同自由度(b)之间的非定域关联(Bell关联);(c)产生和验证自由度间非定域关联的实验方案.Alice和Bob各自制备自旋态为 的原子并使其通过混合分束器.分束器的两个输出分别与本地和对方的分析仪器相连.第二个混合分束器作为各自的分析仪器的一部分,将所得信号组合,在两个粒子的不同自由度中产生了非定域关联.通过CHSH不等式来区别,此时两探测器的信号同时响应.图取自文献[122]Fig.8.(a) Hypernonlocality represents the simultaneous presence of Bell correlations among more than one DOF of two spatially separated particles;(b) hybrid nonlocality identifies Bell correlations among the discrete DOF of one particle and the continuous DOF of another distant particle;(c)experimental scheme for the generation and verification of inter-DOF entanglement.Alice and Bob both prepare one particle in a spin- state and submit it to a hybrid beam splitter.One of the output ports is sent to their local laboratory while the other is send to the opposite party.By mixing the local and the received copy using a second hybrid beam splitter,the desired correlations are established. Both parties now measure either spin or external d.o.f of their received particles,as depicted by the interchangeable measurement devices (white boxes).The recorded data from the events in which both parties receive exactly one particle violate a suitable CHSH inequality,independently of the measured DOF Adapted from Ref.[122].

3 量子增强的原子干涉仪

即使不考虑多原子体系中的量子纠缠特性,利用超冷原子体系作为量子计量的载体,就已经充分利用了它的一个基本量子属性——全同性.因此一定意义上实现了具有量子增强的量子计量:由于全同的超冷原子体系本身就是一个非常难得的、与参数测量要求完全相同的多粒子统计初态[49].利用其完成一次测量所获得测量精度的提高与系统中原子数的根号成正比(频率或时间测量中利用光格子将原子分开,亦是相同的道理).这也是利用超冷原子气体的原子干涉仪进行重力、微磁场以及时间频标或者原子钟等进行计量研究的一个原因.无论在光子还是原子体系中,对精密测量而言,干涉仪都是一个非常重要的工作框架.因此,本小节将简要回顾有关SU(2）干涉仪的工作原理,再对我们建议的多模式原子干涉进行简要介绍.

3.1 SU(2）干涉仪

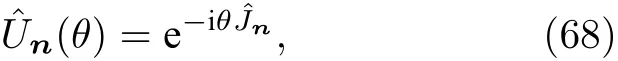
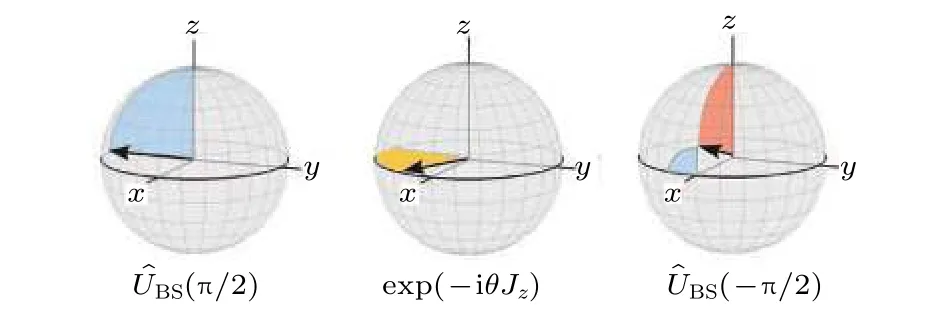
图9 广义 Bloch 球上马赫-曾德干涉仪和拉姆齐干涉仪对集体自旋的操作.图取自文献[5]Fig.9.Representation of Mach-Zehnder and Ramsey interferometer operations as rotations of the collective spin on the generalized Bloch sphere.Adapted from Ref.[5].

一个标准的线性、无损的SU(2）干涉仪通常有两个输入和两个输出端口,可用下面的矩阵运算来表示

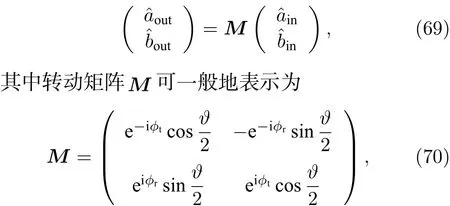
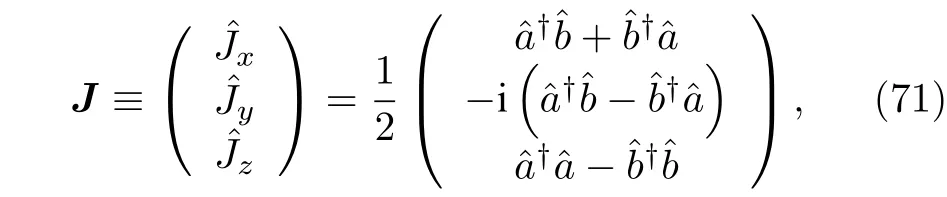
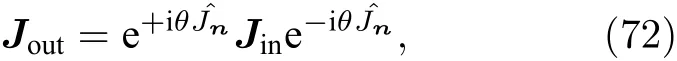
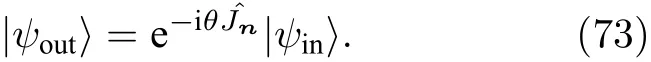
1）对称分束器.对于一个完全对称的分束器,对两个不同输入态有完全相同的作用,可以利用(69）式来表示.其对称矩阵(70)式中的两个角度分别为,,

3.2 原子干涉仪

相较于光学、电子以及中子干涉仪,原子干涉仪具有原子种类多,光学散射截面大,对电、磁环境灵敏度高和易于测量等特点.从上世纪70年代开始,在对原子的波动特性和其质心运动的相干控制有了一定积累之后,对原子干涉仪[22]的相关研究取得了长足的进步.目前原子干涉仪已经成为基础量子理论、精密测量以及原子分子物理研究中的重要手段[22,126].原子干涉仪的实验实现一定意义上展现了人们对原子波动性相干操控的能力.关于它的相关研究和综述很多,有兴趣的读者请参考文献[22,126,127].本文扼要介绍其工作原理以及一些主要进展.

1）主要组成过程.基于上述SU(2）干涉仪的原理,原子干涉仪是将原子特定量子态(内态或动量态)上累积相位精确读出的仪器,主要由以下几部分组成:I)初态(长寿命内态或是动量态)的选取;II)相干原子分束,通过光栅衍射方法实现;III)自由演化阶段,即相位差累积过程(在这个过程中,将待测量的物理量与原子内态或动量态进行耦合);V)相干复合过程,将不同路径上的原子进行态叠加;VI)测量过程,通过测量不同态上的粒子数,获得干涉条纹并读取相位差信息.需要注意的是,依赖于不同测量物理量的原子干涉仪进行相干操控的量子态并不相同,比如:测量时间频率标准时,关注的量子态为原子的内态;而在重力等惯性力的测量中,则是其平动量子态(动量态)[22,126].

2）相干原子分束.通过降温和速度选择等方法,原则上可以得到具有较好空间分布的原子初态.根据不同原子干涉仪的用途,还需对原子云进行进一步的操作以获得理想的原子初态.一般来讲,原子相干分束通过衍射(diffraction)过程来实现.早期的原子衍射选用特定的晶体或微纳结构的光栅器件来实现[22].近年来,光与原子相互作用成为原子相干分束的主要手段,下面对其中的两类相互作用进行简单介绍:Raman-Nath近似的光格子作用和速度选择的受激拉曼跃迁作用.在原子束与光场的相互作用中观察到原子的衍射现象[128,129]以后,原子与光的相互作用才被认为是一种相干原子分束的有效手段[22],即光格子对原子束也可起到光学镜片对光一样的作用.一个两能级原子与光场的相互作用的有效势函数可以写为

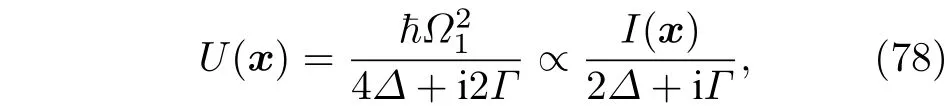
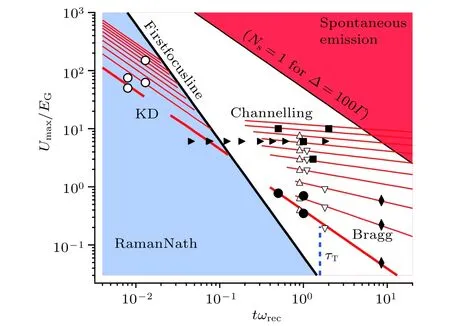
图10 无量纲参数下的原子衍射图:KD 衍射和 Bragg 衍射所满足的条件.图取自文献[22]Fig.10.Dimensionless parameter space for atom diffraction,KD labels curves corresponding to conditions that maximize Kapitza-Dirac diffraction,and Bragg indicates curves that correspond to conditions for Bragg reflection.Adapted from Ref.[22].

3）受激拉曼型的原子干涉仪.由于上述的双光子拉曼过程对原子平动动量有一个小的改动,因此这个过程也被称为与速度依赖的拉曼转移过程.将这个过程用来对超冷原子进行相干分束、复合等操作,就是目前原子重力干涉仪的工作原理[44,126,130].如图11所示,简单地说,利用第一束拉曼光,将处于的初态原子平均分束为和;经过时间的自由飞行,再利用一个脉冲将两个内态上的原子进行交换,即;再经过相同的自由飞行时间,两原子团将回到相同的地方,再进行另一个拉曼光作用,即完成了该原子干涉仪的基本过程.上述相同的自由飞行时间可以在原子喷泉中得到保证.利用原子干涉仪还可以实现微观粒子弱等效原理检验[131−138].

3.3 多模式原子干涉仪

为了进一步提高原子干涉仪的测量精度,除将量子初态制备为量子纠缠态之外,还可以考虑一些其他的量子效应,达到提高量子测量精度的目的.但是,这种精度的增加,仍然受到标准量子极限的限制,而远未达到海森伯极限的量级.本小节将介绍利用Kaptiza-Dirac(KD)方法对原子进行相干分束操作,同时介绍利用谐振子运动的特性而发展的一种新的多模式原子干涉仪[140].

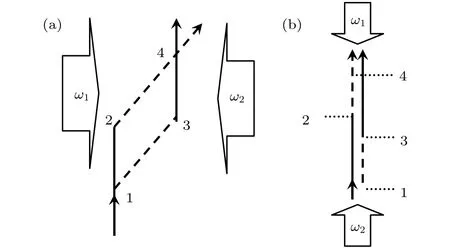
图11 (a)马赫-曾德原子干涉仪示意图;(b)重力计原理示意图.图取自文献[139]Fig.11.(a) Schematic plot of Mach-Zehnder atom interferomery; (b) schematic plot of Gravimeter configuration.Adapted from Ref.[139].

1）多模式干涉仪.标准量子极限(58）式表明,增加统计独立的测量次数或者增加参与测量初态的粒子数均可以有效地提高测量的精度.在光学干涉仪中,还可以通过提高入射激光的功率来提高测量精度(已经在LIGO的引力波测量中被提及,当然也特别采用了非经典光来提高测量精度),因为激光功率增加相当于输入了更多的光子.相较于提高光子数目,在实验中增加原子初态的原子数目就没那么容易了.有别于输入非经典态或量子纠缠态,利用多模式或是多通道干涉仪的方法来提高测量精度也逐步引起人们的注意[141,142].在光学干涉仪中,通过多模式的分束器、或是多路的干涉光源,已经发现类似的测量精度的提高,其中是模式或者光源的数目[142].这样的测量精度的提高虽与突破散粒噪声极限无关,但是由于比多原子量子纠缠态稳定、易操作,还是受到人们的关注[49].利用光格子囚禁的超冷原子气体,也被建议用来实现模式的原子干涉仪[143],此时为囚禁冷原子的光格子的数目.处在不同格点位置的原子,自然成为探测不同点重力参数的探针,计算表明其测量的精度可以达到.

2）Kaptiza-Dirac 多模式原子干涉仪.如前所述,KD光脉冲提供了一种将超冷原子在不同动量态上进行重新相干分布的方法.同时,虽然光与原子的作用时间相对短,但是KD效应已经在很多实验室被观察到,如图11所示.在原子喷泉实验[144]中,要保证更多的原子处于完全相同的动量初态,原则上也需要更低的实验温度.相对较长的作用时间也在一定程度上增加了原子量子相干性保持的难度.特别是原子的扩散过程,会造成有效原子数目的减少.综合考虑上述原因,我们在2014年建议了一种新的多模式原子干涉仪的实验方案,特别考虑了KD光与原子相互作用的特性以及在谐振势中粒子运动的特点.如图12所示,利用谐振势中粒子运动的周期性,可以有效减少由于光脉冲相互作用导致的光子数损失.

2）主要过程:I)初态制备,处于谐振势中的超冷原子气体(无相互作用);II)KD相互作用的原子分束器,纯相位器件;III)自由演化,多路的相位累积过程,相邻两路之间的相位差设为相同();IV)在时刻(为谐振子势阱的囚禁频率),加另一束KD光相干叠加不同路径的原子;V)在测量,处于不同动量态的原子数的测量.由于初始原子之间并无相互作用,该动力学过程可以精确求解.利用量子Fisher信息的计算,可以得到对于相位的估计精度[145]为

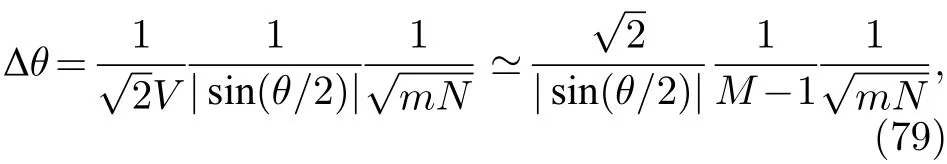
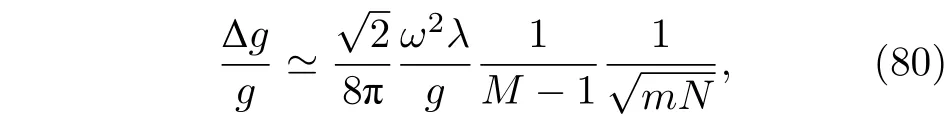
3.4 非局域相互作用的原子干涉仪

1）非局域相互作用.通常情况下原子干涉仪与待测物理量之间的耦合相互作用都是局域的,或者与粒子数成正比,是线性关系,可用幺正变换(68）式来表示.但在一些特定情况下,粒子间的非线性或非局域相互作用也起重要的作用,此时,相位测量精度与探测态中粒子数之间的关系,与这些非线性相互作用的大小与形式均相关,可以满足不同于的关系,其中(SQL)或是1(HL)[147−153].需要指出的是,尽管非线性或非局域相互作用可以导致测量精度与粒子之间新的幂次关系,但仍然满足标准量子极限和海森伯极限(参见文献[5]及其参考文献)(本质上讲,由于这些非线性或非局域相互作用也是产生纠缠或增加Fisher信息的主要原因,因此,我们认为在累积相位的过程中也增加了测量初态的量子Fisher信息或量子纠缠;另外,线性相互作用不会造成量子Fihser信息的增加或量子纠缠).

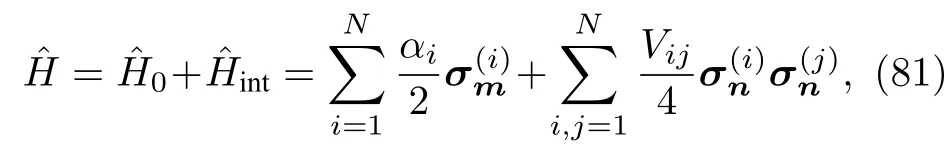
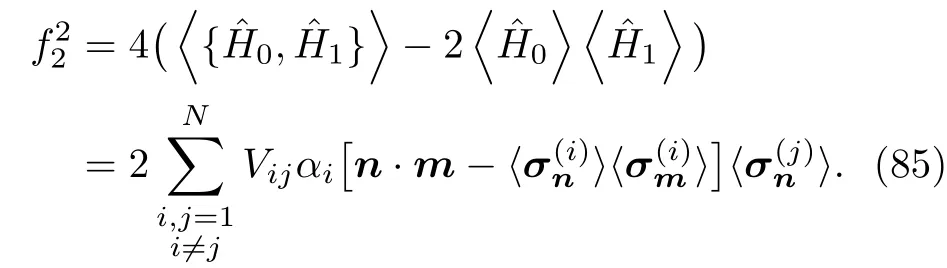
为简单起见,以均匀体系的两种非线性(非局域)相互作用说明这些相位计量精度与非线性相互作 用 强 度 的 依 赖 关 系 .因 此 ,选 择,,这种情况对应于线性原子干涉仪(68）式.同时,将格点相互作用强度并入到相位中,此时非局域相互作用的贡献实际上由其与线性或是局域相互作用量的比值决定.

3）Ising型的原子干涉仪.考虑近邻相互作用且外场与格点自旋方向相同(顺场Ising),即信息的定义,使(82）式取最大值的、可分的量子纯态可写成[84]

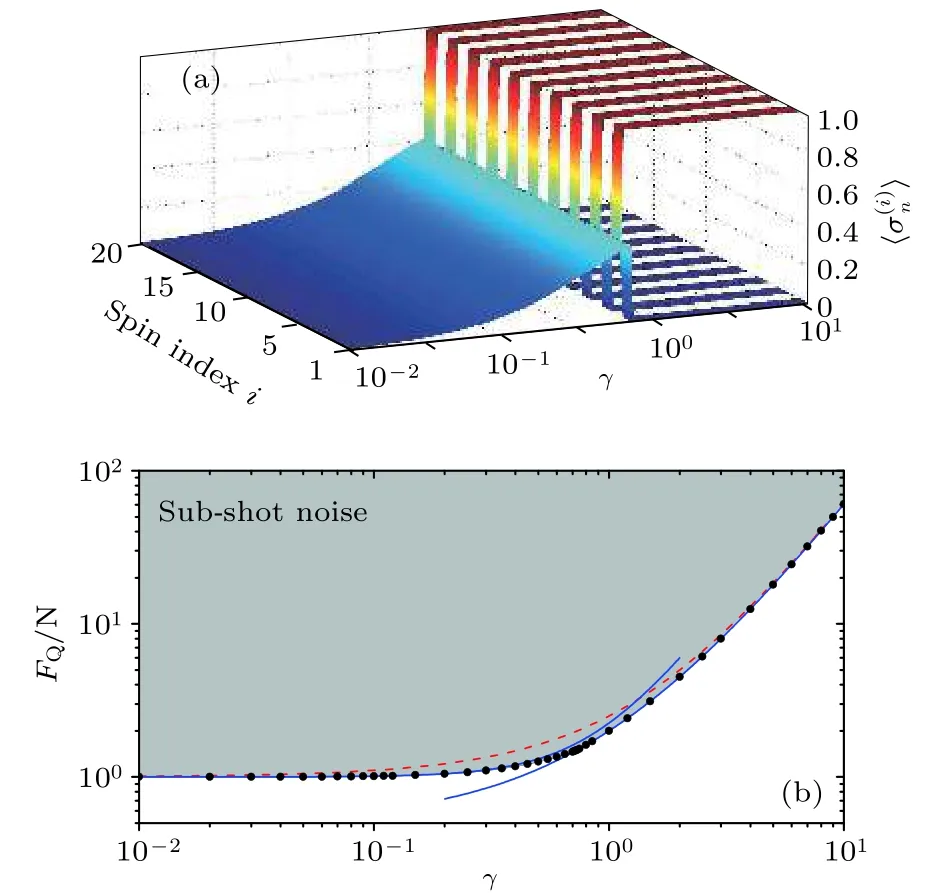
图13 (a)在 Ising 模型中,平均自旋 随 的变化情况;(b) 随 的变化情况,以及标准量子极限和亚散粒噪声极限的边界,同时其也是判定有用量子纠缠态的边界[84].灰色区域为亚散粒噪声区域.图取自文献[84]Fig.13.we show the with respect to ;(b)with respect to the and give the boundary between standard quantum limit and sub-shot noise, which also witnesses the useful entanglement in Ref.[84].The gray region denotes the sub-shot noise region.Adapted from Ref.[84].

图13 及(87）式表明:近邻相互作用下,量子Fisher信息随相互作用强度的变化呈单调关系.尽管在时呈现非线性关系,但是,仍可作为判断多粒子量子纠缠的判据,详细可参见文献[84].同时考虑(87）式以及CRB(15）式可以知道,相位测量精度将依赖于非局域相互作用强度,即

4）LMG型的原子干涉仪.另一种极限情况为,(81）式中的任意两个格点之间存在相等的非局域相互作用,即,同时.该模型最早在核物理研究中提出[155−157],近些年在量子纠缠[158−160]、自旋压缩[113,161]以及量子计量方面[162]都有较为广泛的应用.与Ising情况不同,对于任意给定的耦合强度,不同格点上的自旋平均值相等,即(图 14(a)),使 (82） 式最大.也就是说,系统的量子Fisher信息(82）式可以写为[84]

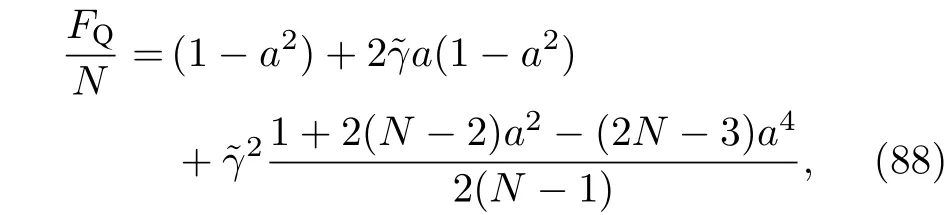
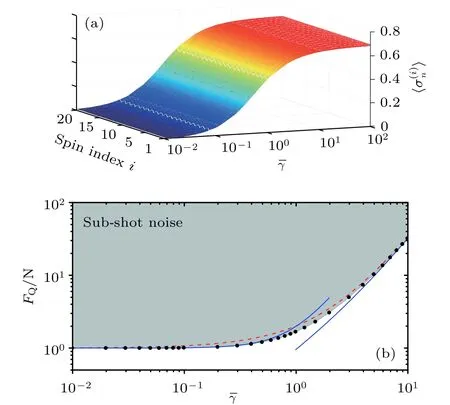
图14 (a)在 LMG 模型中,平均自旋 随 的变化情况;(b) 随 的变化情况,以及标准量子极限和亚散粒噪声极限的边界,同时其也是判定有用量子纠缠态的边界[84].图取自文献[84]Fig.14.(a)We show the with respect to in LMG model;(b) with respect to the and give the boundary between standard quantum limit and sub-shot noise,which also witnesses the useful entanglement in Ref.[84].The gray region denotes the sub-shot noise region.Adapted from Ref.[84].

由对Fisher信息(82）式中各项分别最大化得到,如图14(b)中红色的虚线表示.显然,在给定非局域相互作用以及原子数的条件下,LMG型原子干涉仪可以进一步提高相位测量的精度,因为.利用这种量子Fisher信息与粒子数的单调关系可以区分不同多粒子量子纠缠态的纠缠特性[84].

4 量子计量中的统计方法

相位估计是量子计量,甚至是量子精密测量中的核心环节之一,也是经典统计推断(statistical inference)中的一个重要分支.如果待测参数在测量过程中不随时间变化,这类参数估计问题为静态参数估计问题[163],比如重力、引力常数等;当然还存在测量过程中变化的参数估计,此类问题不在本文讨论的范围(典型的问题应为时间频率标准中的估计,此类问题被称为warm-function估计).对于第一类问题,即待测参数在测量过程中为常数,通常有两类不同的估计方法:一种称为贝叶斯(Bayesian)估计,另一类称为频率(frequentist)论估计或Fisher估计,也被称为非贝叶斯估计.由于两种估计方法处理数据的出发点完全不同,因此,不同的方法可能导致不同的结论甚至悖论式的结论.相位估计所处理的数据都具有随机数的特性,它的主要任务是要从这些具有随机特性的实验数据中,将所关心的待测物理量高精度地估计出来.一般将测量数据的随机性归结为噪声(noise).有两类完全不同的噪声:一类为经典噪声;另一类为量子噪声.其中第一类噪声是固有的,由仪器或操作的不完善造成,是可以压缩到零的;而第二类噪声是本质的,由量子力学原理所决定,是不可克服的[164].

4.1 频率论估计

来评估[166].注意 (93） 式中,待测量相位值并不事先可知,因此,与 (92）式比较就有

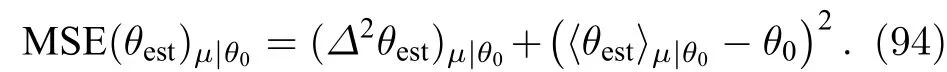
从这个角度上讲,(92）式更具有实验的可操作性.对于无偏差的估计子而言,(92）式和(94）式是等价的.由于 (94）式中,所以有.也就是说,任何小于

2）Barankin 极限.经典统计理论给出 (92）式的方差存在一个极限,称为Barankin极限[167,168]

4.2 贝叶斯估计

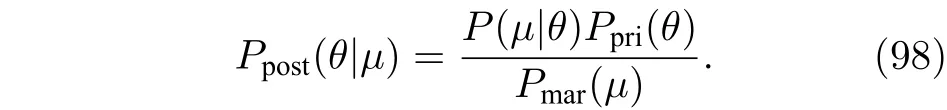
需要指出的是,后验分布函数对先验分布函数有非常强的依赖性.如果对待估计参数一无所知,那么选取一个合适的先验分布函数并不是一件容易的事情.也就是说,并非简单选择一个常数作为分布函数即可,详细的讨论参见文献[164].但是,如果得到(98）式的后验分布函数,可以利用找极值的方法得到估计的:.当先验分布为常数时,此法与最大似然估计∫相同,也可以通过对后验分布求平均值来获得估计值.

与频率估计方法不同,利用贝叶斯估计方法,可以得到一个关于估计值的置信区间(confidence interval)(在测量次数很大时,它与涨落具有相似的含义)

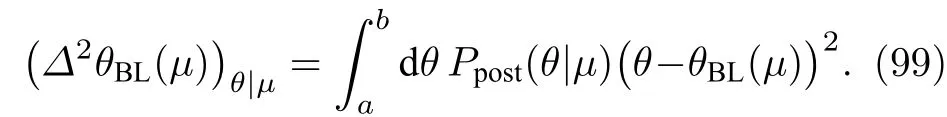
2）Ghosh 极限.1993 年,Ghosh[172]证明 (99）式存在下限

4.3 数值验证

1）最大似然分布函数.下面采用与离子实验[92]相关的宇称测量结果(51）说明前两节中提到的各种统计极限.考虑?离子的 GHZ 纠缠态,,作为初态,再对其进行 (68）式描述的的转动操作.对于转动相位,通过对宇称性 (,为在上的粒子数) 的测量来估计.测量值的条件概率函数由(51）式给出,因此,经过次独立测量所得到的似然函数为

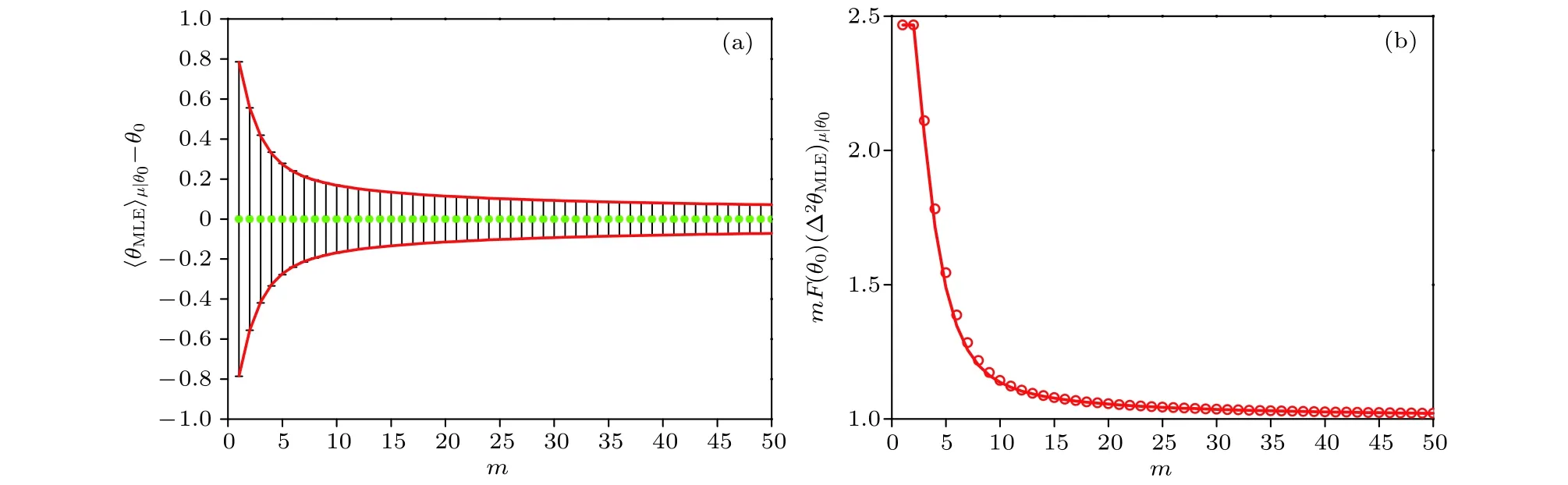
图15 (a)最 大 似 然 估 计 偏 差 (绿 色 圆 点 ) 随 独 立 测 量 次 数 的 变 化 ,误 差 为 ;红 色 曲 线 为;(b) (空心红圈) 随 的变化.红色实线为 .图取自文献[164]Fig.15.(a)Bias (green dots)as function of with error bars .The red lines are (b) variance of the maximum likelihood estimator multiplied by the Fisher information,(red circles),as a function of the sample size .It is compared to the bias (red line).We recall that and here.Adapted from Ref.[164].

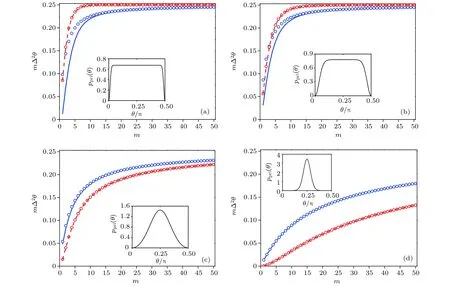
图16 不同先验概率下,频率论方法得到相位估计值的方差( ,红色圆圈) 及其边界 CRB( ,红色虚线),和贝叶斯相位估计的方差 ( ,蓝色圆圈) 及其边界 ( ,蓝色实线) 随样本 的变化(a) ;(b);(c) ;(d) .每张图中内嵌的图是先验概率 的分布图.图取自文献 [164]Fig.16.Comparisons of phase estimation variance as a function of the sample size for Bayesian and frequentist data analysis under different prior distributions:(a) ;(b) ;(c) ;(d) .In all figures,Red circles(frequentist)are,the red dashed line is the CRB. ,Eq.(124）.Blue circles(Bayesian)are ,the blue solid line is the likelihood-averaged Ghosh bound ,Eq.(103）.The inset in each panel is .Adapted from Ref.[164].

5 总结与展望

利用超冷原子系统突破标准量子极限是一个充满生机与挑战的多学科交叉研究领域.在实验方面,已经完成了若干利用多粒子纠缠态提高测量精度、趋近海森堡极限的验证性实验,未来的研究可能集中到将其扩展到具体的物理参数测量的系统中.理论方面,基于量子Fisher信息的多粒子量子纠缠态判据以及相关的量子计量基本理论仍需进一步发展,同时也需要关注相关的量子效应,以提高物理量的测量精度.由于该领域发展很快,这里简单介绍一下最近在理论方面的几个进展.

1）连续变量纠缠判据.量子 Fisher信息已成功地应用在分离变量的量子系统中的多粒子纠缠判据和量子参数估计中[4,174].考虑到Fisher信息与测量物理量测量精度之间的关系((9）式),Fisher信息已经被推广到连续变量的纠缠判定[82,175].考虑一个模式的连续变量系统相空间.相应的算符矢量为义为

因此(110)式及(112）式就是连续变量条件下的多粒子纠缠判据.该判据的有效性,已经得到利用2–-4不同组份压缩光实验结果的证实[176].

2）多变量参数估计.前面关于标准量子极限、海森堡极限的进展是基于单参数的相位估计理论.同时对多个参数估计的研究才刚刚开始,由于其在量子成像和探测等方面有重要应用前景,多变量的相位估计正在引起人们的关注[177−180].在多变量的参数估计问题中,要考虑对一个维的矢量进行估计.此时要讨论的条件概率分布函数也是多变量的,此时无偏估计子满足相应的CRB写为

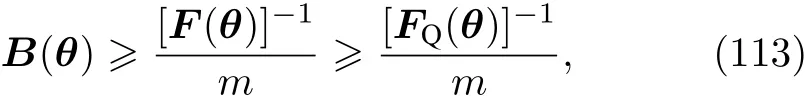
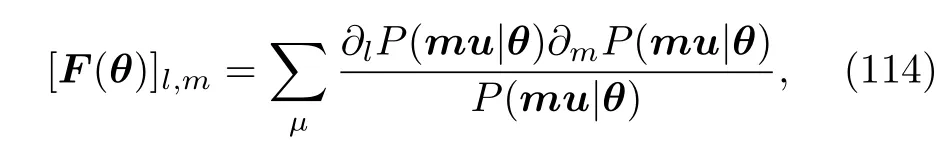
3）含时参数估计问题.在测量时间内,如果待测物理量是随时间变化的,那么是否存在一个测量极限？如果存在的话,它是多少?随时间变化的待估计相位在引力波测量、磁场力、光力系统等过程中都是常见的,因此,近几年引起了人们的关注(参见文献[181],及其参考文献).随时间变化的相位也被称为波形(waveform)问题,连续的测量才可能提取其随时间变化的信息.Tsang等[181]2011年将Bayesian分析方法引入到含时问题的估计中,并给出一个量子 CRB.需要指出的是,对光频率钟的测量过程中也存在相应的问题.由于钟激光不可避免地存在随时间的频率变化,因此,如何对其随时间的变化进行测量是对其实现稳定性控制的关键问题.一般地,含时待测物理参数更具有一般性,如何发展具有普适性的、严格的计量理论仍是一个开放的问题.

4）关于统计方法.由前面的讨论可以知道,在有限次测量的条件下,要达到统计允许的最佳测量精度是比较困难的,或者说对测量数据的分析方法有较强的依赖性.对实验测量数据的统计分析有很多种方法,不同的统计方法可能导致不同的边界.如何在统一的标准量子极限或海森堡极限下理解这些极限,也是一个有挑战的研究课题.如前所述,若测量算符为有偏差测量时,上述极限原则上不正确,需要更一般的讨论[182].近年来,非高斯情况下的统计特性逐渐成为研究的热点,与此相关的量子Ziv-zakai边界是其中的热点之一[183].在考虑非渐近的体系时,则需要考虑Weiss-Weinstein边界[184].

简而言之,超冷原子体系中的量子计量不只是一个技术问题,还与许多基本的量子效应、甚至量子理论的基本概念息息相关.因此,它是一个非常有活力的研究领域,是下一代精密测量仪器产生的源泉.

感谢山西省百人计划专家、意大利科学院光学研究所Smerzi研究员,山西省百人计划青年学者、意大利科学院光学研究所Pezze博士,以及意大利科学院光学研究所Gessner博士的讨论与建议.

附录A1

附录A2

附录A3

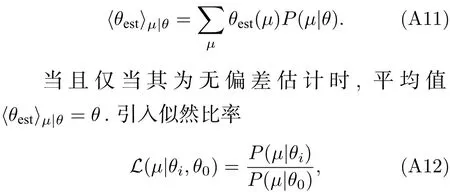
可以得到

这样(95）式得证.