福州市中心城区交通拥堵程度识别研究
2019-03-15赵银柱谢幸林涂锦程李承洲
■赵银柱 谢幸林 涂锦程 李承洲 王 锋
(福州大学土木工程学院,福州 350116)
1 绪论
近年来,城市化水平快速提高、机动车保有量爆炸式增长,道路基础设施无法满足出行需求,城市交通拥堵越发严重。而城市的中心城区作为城市的政治文化中心和重要经济功能集中体现的地区[1],是交通流最为密集复杂的区域,它所面临的交通拥堵问题也更为严峻棘手。通过大量新建道路基础设施以及扩大原有道路车道数等手段,将会加剧机动车的增长,使交通流量持续上升,恶化交通出现拥堵。因此准确识别中心城区拥堵程度,对交通管理、交通疏导、提高道路通行能力具有重要的意义。
Hawas等[2]以模糊性数学理论为基础,通过计算聚类隶属函数来监测城市道路交通事件,可行性高且缓堵作用显著。Bauza等[3]基于对车辆联网、车辆感知范围等研究,借助模糊分离器分析描述路段交通拥堵程度。Kong等[4]基于卡尔曼滤波理论,对道路检测器与车辆GPS检测器的原始数据进行预处理,通过GIS系统匹配速度与流量以识别交通状态。黎符忠[5]建立了城市道路交通拥堵评价体系,包含交叉口、路段、区域指标,结合信息熵权值法与灰色理论,构造灰色关联度评价模型,方案实施效果良好。刘志刚、金升[6]运用博弃论理论分析城市拥堵问题的产生原因,指出拥堵根源是“囚徒困境”,以及总结了四种城市拥堵解决对策。龙建成[7]构建动态的路网交通流传播模型,研究交叉口的紧急交通流的传播,构建了交叉口交通模型以及动态随机路径选择模型。
本文在数据调查分析的基础上,以模糊数学为基础、隶属函数为工具,建立模糊综合评判模型,对中心城区拥堵状态进行识别,为交通拥堵管理提供依据。
2 中心城区的相关问题
2.1 中心城区的界定
中心城区是所在行政区域城镇体系中处于主导地位的城市建成区范围,是具有城市政治、经济、文化、社会引导功能的集中承载地区[1]。2017年11月3日通过的《福州中心城区空间发展规划》,福州中心城区总面积约2881km2,范围为:福州市辖五区,长乐全域,闽侯县9个乡镇街道,以及连江县琯头镇[8],论文研究范围为主城中心区。
2.2 中心城区道路系统
中心城区道路系统是城市道路系统的重要组成部分,可以依照《城市道路交通规划设计规范》,将其划分为:快速路,主干路,次干路,支路。
以上四个等级城市道路的可达性与机动性关系见图2。
交叉口是道路与道路的相交节点,将各条道路相联结形成路网。交叉口是道路通行能力的瓶颈,制约道路甚至路网的服务水平。结合本文的研究内容,将研究对象定位为中心城区的主干路。
3 中心城区交通拥堵的模糊综合评判模型
3.1 评价指标集的确定
结合评价指标选取原则,确定该模型评价指标集为:U={u1,u2,u3,u4}={D,S,Z,T}={路段拥堵延时指数,路段饱和度,交叉口饱和度,交叉口延误时间},中心城区交通拥堵度的评价指标体系如图3所示。

图1 福州中心城区空间结构示意图
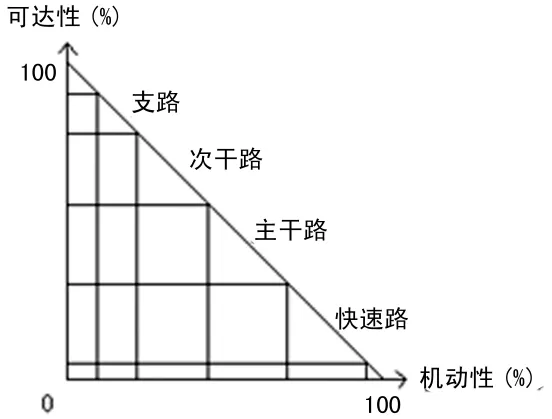
图2 不同等级道路的机动性与可达性
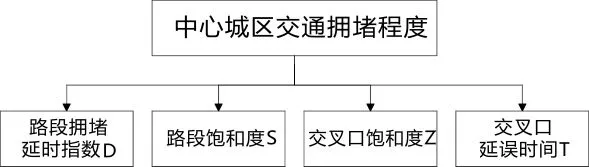
图3 中心城区交通拥堵评价指标体系
3.2 评判标准的建立
根据交通拥堵等级评判的标准,将中心城区交通拥堵程度划分为畅通、缓行、拥堵、堵塞,即确定该模型的评判标准集为:V={v1,v2,v3,v4}={畅通,缓行,拥堵,堵塞}。
3.3 隶属函数的构造
隶属函数是基于模糊集合而发展的,模糊集合运用隶属函数rA(x)来描述元素对模糊集合的隶属程度,隶属程度的取值是[0,1]。隶属函数可以表示属于的概念,即rA(x)=1;也可以表示不属于的概念,即rA(x)=0;还可以表示模糊临界的概念,即rA(x)∈(0,1)[9]。隶属函数的数学表达公式如下:
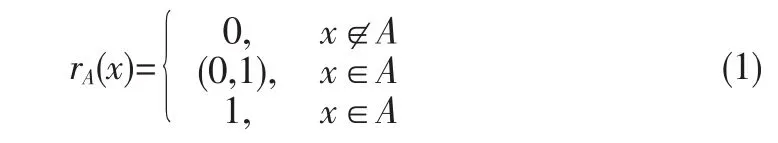
在模糊性数学理论中,常用的隶属函数有梯形函数、三角形函数、S型函数和正态函数等。由于梯形隶属函数具有容易理解、计算简单、分辨率高、性质稳定等优点,故选取梯形隶属函数。
3.3.1 梯形隶属函数的构造方法
隶属函数的精确度取决于模糊分级,即精确划分属于区间、模糊临界、不属于区间。如图4的梯形隶属函数,Fk的属于区间为,模糊临界为与,不属于区间为与
3.3.2 中心城区交通拥堵程度的模糊分级
借鉴目前正在使用的交通拥堵量化标准,运用模糊分级的方法,对中心城区交通拥堵程度做出如下的量化分级,如表1所示。

图4 梯形隶属函数的一般形式

表1 中心城区交通拥堵程度的模糊分级
3.3.3 路段拥堵延时指数的隶属函数
由表1可知,路段拥堵延时指数为D∈[1.0,1.4]时呈现畅通状态,D∈[1.6,1.8]时呈现缓行状态,D∈[2.0,2.2]时呈现拥堵状态,D∈[2.4,+∞]时呈现堵塞状态。其余区间为相邻交通状态的模糊临界,呈现“亦此亦彼”的交通状态。路段拥堵延时指数的隶属函数如公式(2)如所:

因此路段拥堵延时指数D的模糊关系向量R1=(r11,r12,r13,r14),其中每个r1j分别代表路段拥堵延时指数 D对畅通、缓行、拥堵、堵塞的隶属程度。
3.3.4 路段饱和度的隶属函数
路段饱和度的隶属函数如公式(3)所示,r21、r22、r23、r24用以计算路段饱和度S对畅通、缓行、拥堵、堵塞等状态的隶属程度。
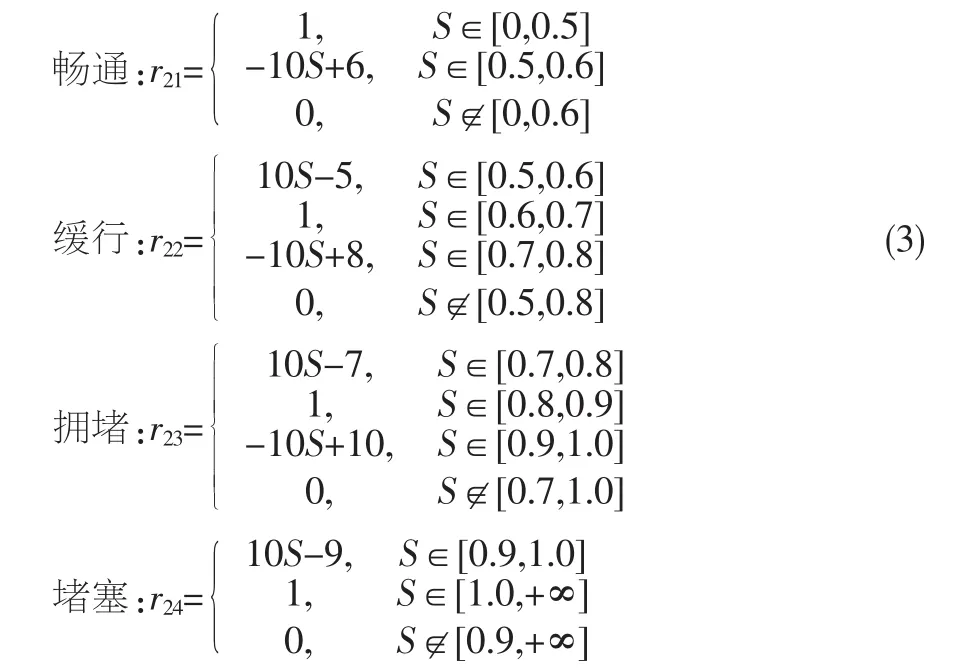
3.3.5 交叉口饱和度的隶属函数
由表1可知,交叉口饱和度Z与路段饱和度S的量化分级取相同数值,所以除了自变量的定义与取值不同之外,交叉口饱和度Z的隶属函数图象、公式与路段饱和度S基本一致,交叉口饱和度的隶属公式如式(4)所示。


故,交叉口饱和度Z的模糊关系向量R3=(r31,r32,r33,r34),其中每个r3j依次代表交叉口饱和度Z对畅通、缓行、拥堵、堵塞的隶属程度。
3.3.6 交叉口延误时间的隶属函数
交叉口延误时间如公式(5)所示。

故交叉口延误时间T的模糊关系向量R4=(r41,r42,r43,r44),其中每个r4j依次代表交叉口延误时间T对畅通、缓行、拥堵、堵塞的隶属程度。
3.4 指标权重的确定
在考虑用于评价中心城区交通拥堵程度的指标时,交叉口饱和度最为重要(34%),继而依次为交叉口延误时间(32%)、路段饱和度(18%)、路段拥堵延时指数(16%)。 通过判断矩阵一致性检验,可以确定评价中心城区交通拥堵程度的指标权重集为:W={w1,w2,w3,w4}={w路段拥堵延时指数,w路段饱和度,w交叉口饱和度,w交叉口延误时间}={0.16,0.18,0.34,0.32}。
3.5 模糊合成值的计算方法
模糊合成值的计算模型为 ,式中δ称为广义模糊算子。在数学理论中存在无穷多种广义模糊算子,实际运用中常见有以下4种。

表2 广义模糊算子
故,选择M(●,⊕)进行模糊合成值的计算,它综合考虑主次因素且得到的模糊合成值B具有归一性。
3.6 模糊综合评判结果的确定方法
两种确定模糊综合评判结果的方法见表3,本文选最大隶属度法。

表3 模糊综合评判结果的确定方法
4 模型的运用
4.1 数据调查
本文选取福州鼓楼区位于劳动大厦附近的一条城市主干路——古田路作为研究对象,路段(含交叉口)长度为0.784km。调查时段取工作日晚高峰,每15min统计一次交通数据。在调查路段的起终点各安排调查人员,读取车辆经过路段的时间以及记录车牌的后三位。数据整理阶段将观测数据按照相同车牌号进行匹配,车辆通过路段首尾时间得到行驶时间相减,结合路段长度,多组数据取平均值得到行程车速。以停车线为观测断面分车种分流向进行交叉口交通量调查。通过记录在停车线后面的车辆数及经过停车线的停驶数和不停驶数进行交叉口延误时间调查。统计结果如表4所示:
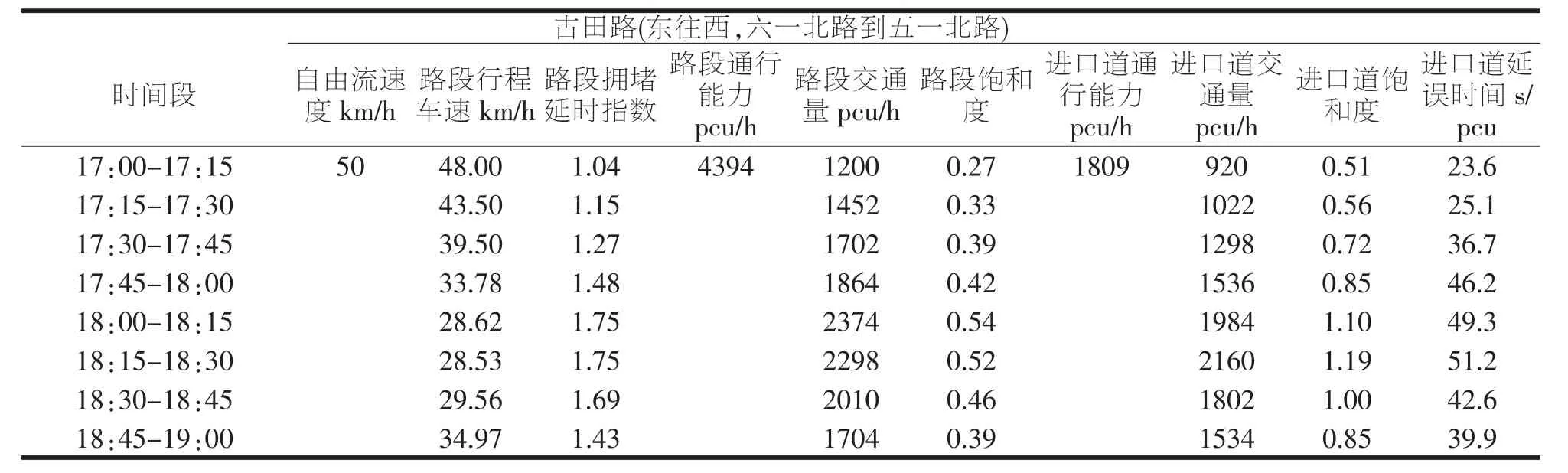
表4 交通数据汇总表
4.2 模型分析
将统计数据带入模糊综合评判模型中计算,计算过程如下:
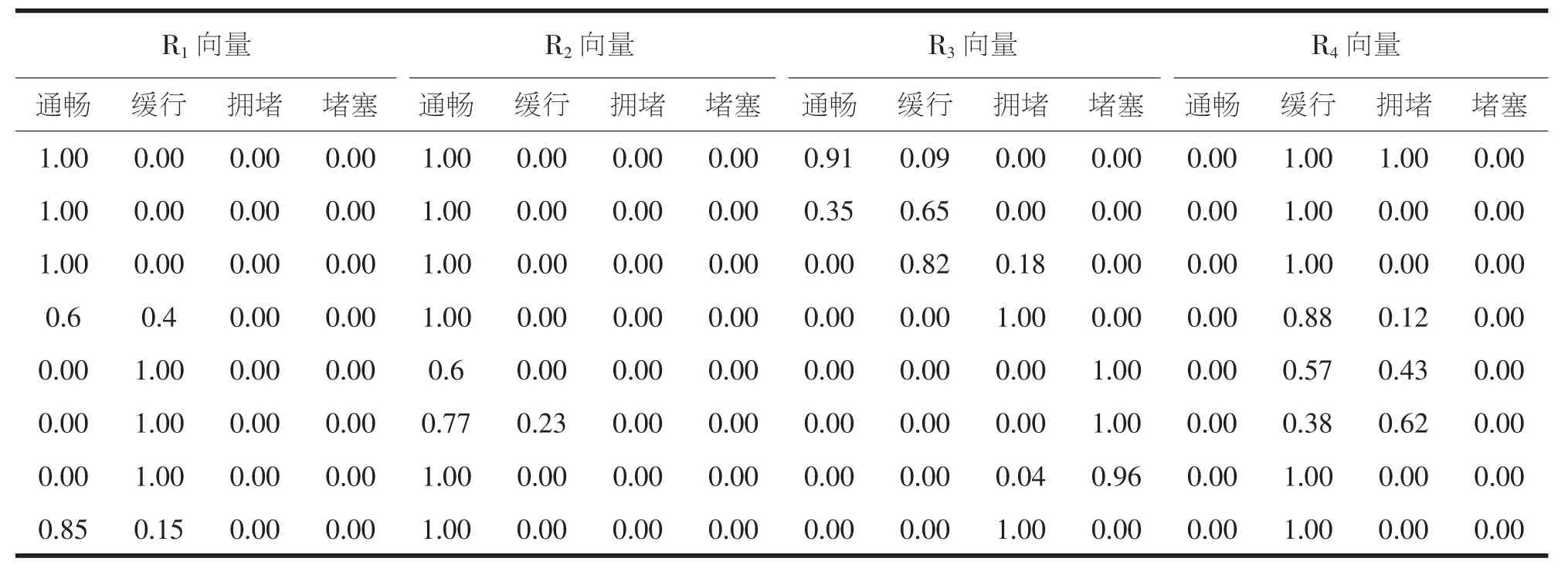
表5 计算模糊合成值

表6 模糊综合评判结果
4.3 结果对比
最终用模糊综合评判模型统计分析的交通拥堵情况下,将其与福州交警app公布的实时路段及交叉口交通状态进行对比,评判结果基本一致,故该模型具有一定可行性.

表7 模型计算结果
4.4 模型运用
用该模型计算鼓楼区其他路段的拥堵程度,见下表8:
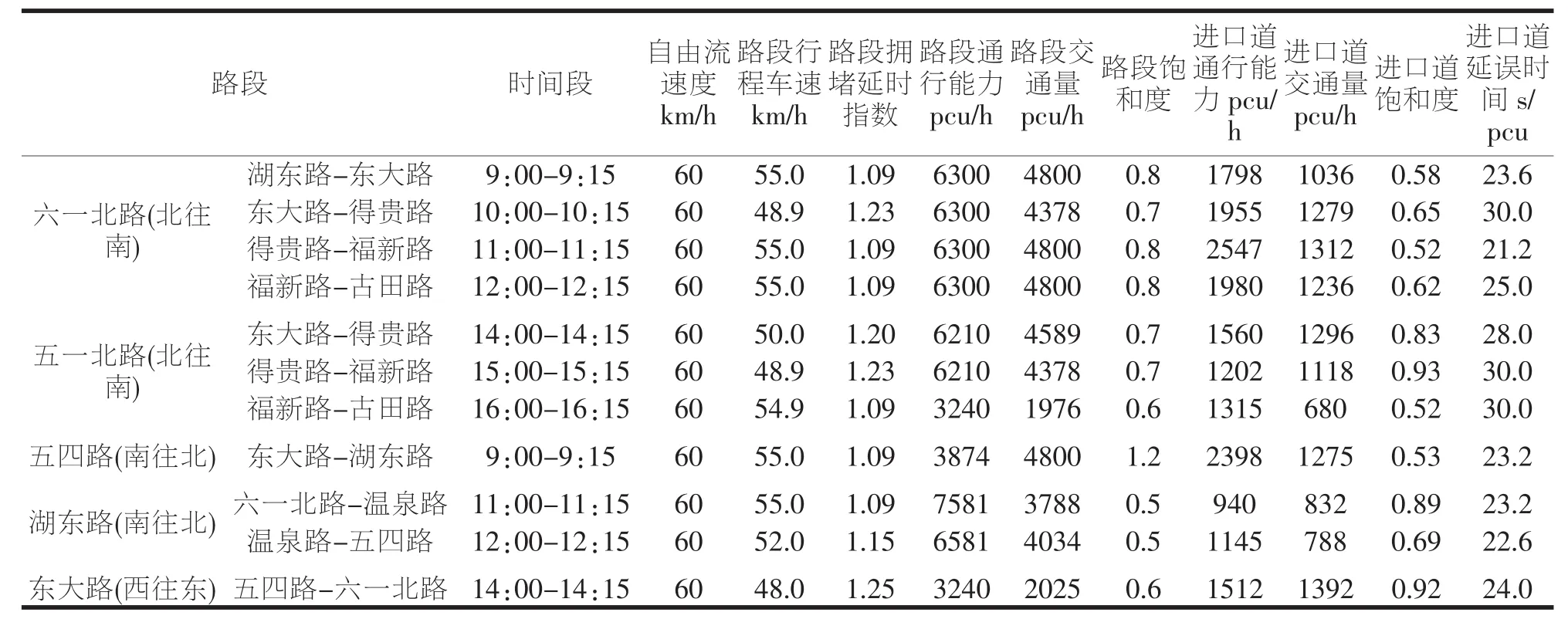
表8 计算模糊合成值
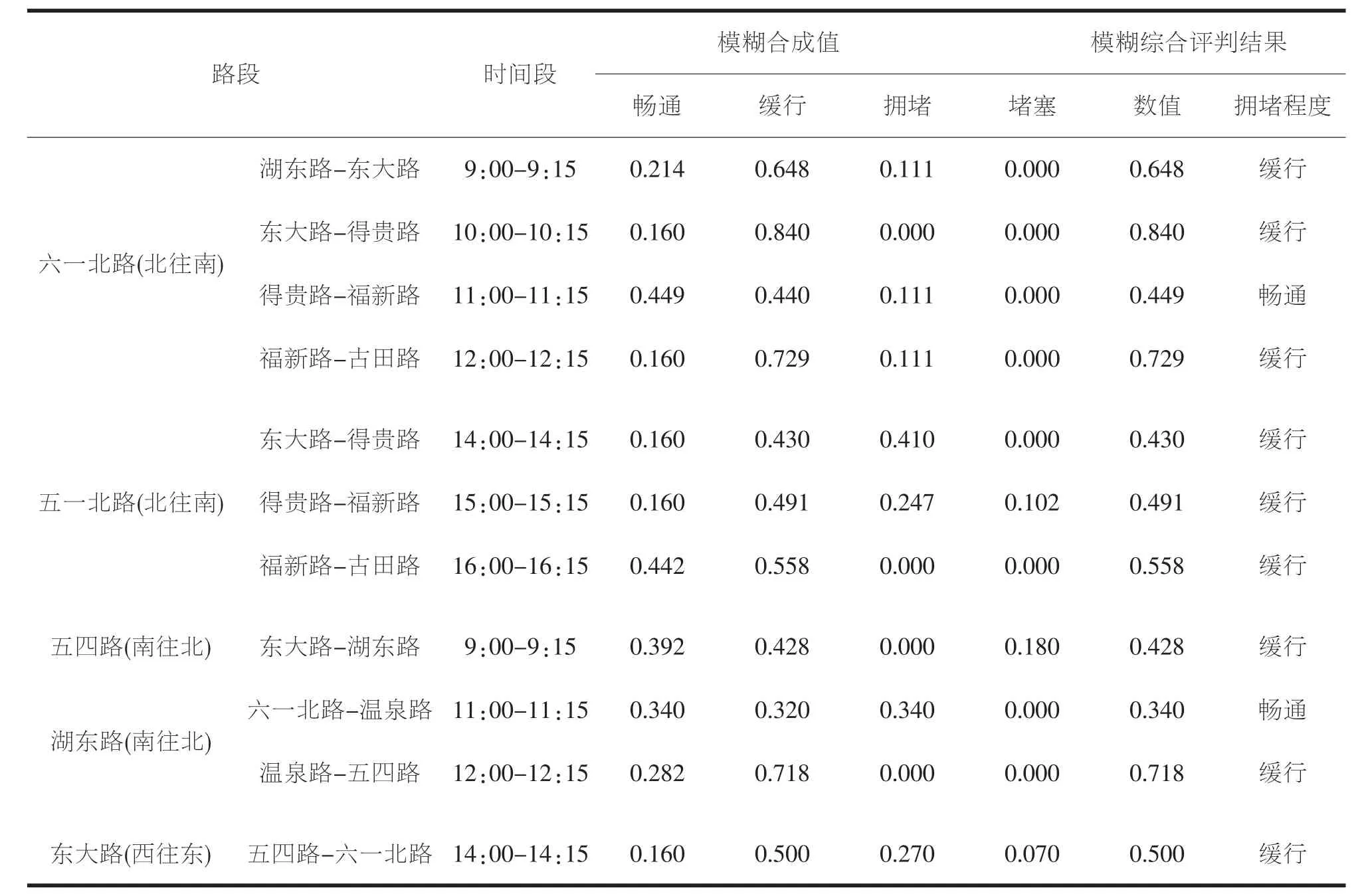
表9 模糊综合评判结果
5 结语
中心城区交通畅通的作用和重要性日益凸显,其拥堵程度识别的研究存在很大的价值,通过模糊综合评判法的模糊综合评判模型对主城中心区交通拥堵等级进行评价,主城中心区几条主干道在工作日晚高峰基本处于缓行和拥堵的状态。
