南京南站振动响应特性研究*
2019-03-15崔聪聪雷晓燕
崔聪聪 雷晓燕 张 凌
(江西省交通设计研究院有限责任公司,330052,南昌//第一作者,助理工程师)
高架车站既不是单纯的房屋建筑,也不是单一的桥梁结构,而是房建与桥梁融汇在一起的一种特殊结构。按照结构体系不同,轨道交通高架车站可分为“建桥合一”和“建桥分离”两大类。作为一种特殊的建筑形式,有必要对其振动特性进行研究。
文献[1]以天津西站为研究对象,建立列车-轨道-站房耦合系统整体力学分析模型,考虑列车与客运站之间的动力相互作用,研究列车高速过站时列车和站房的动力响应。文献[4]考虑了车辆与结构的耦合作用,通过动力仿真软件对新杭州东站进行数值模拟分析,求得结构的振动响应。文献[5]通过将“车辆-桥梁-结构”相互作用系统分解为“车辆-桥梁”系统和“桥梁-结构”两个系统对新长沙站进行结构仿真,并提取车站结构在列车荷载作用下的振动响应。
本文以南京南站为研究背景,从模态分析、谐响应分析两方面研究综合枢纽车站自身的特性。采用无砟轨道双层梁模型进行数值模拟,并将轮轨力加载到有限元模型上来研究车致振动的响应特点。
1 南京南站的动力特性分析
1.1 有限元模型的建立
南京南站主体结构由下到上依次为地下层、轨道层、高架层和高架夹层。建筑外墙南北长450 m,东西宽156 m。候车厅层位于整个站房结构地上二层。
南京南站有限元模型(见图1)中的钢轨采用空间梁单元 BEAM 188模拟,钢轨扣件和轨道板支座采用弹簧阻尼单元COMBIN 14模拟,轨道梁采用实体单元SOLID 45模拟,上部结构中的梁、柱和杆件采用 BEAM 181单元模拟,各层楼板采用SHELL 163单元模拟。

图1 南京南站有限元模型图
1.2 模态分析
根据南京南站有限元模型得到结构层的自振频率与振型,如表1所示。
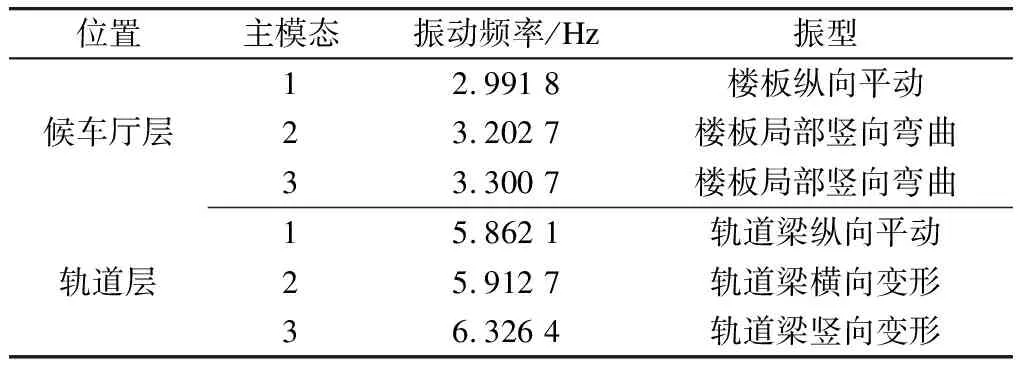
表1 南京南站自振频率与振型
1.3 谐响应分析
采用Rayleigh阻尼(比例阻尼)进行结构动力计算,根据模态分析计算得到α为0.314,β为0.007 9(α、β分别代表与质量、刚度成比例的阻尼系数)。
谐响应分析在有限元模型上的具体加载形式为:全线考虑1个轮对,每个轮对各施加1个幅值为10 kN的作用力;取荷载频率变化范围为0~80 Hz,并按1 Hz求解一次。提取车站结构楼板振动敏感点,并对楼板关键点在谐响应下的位移、速度和加速度进行分析。
本文仅选取跨度为24 m楼板的跨中位置进行分析,相应的位移导纳、速度导纳、加速度导纳随着频率的变化如图2所示。
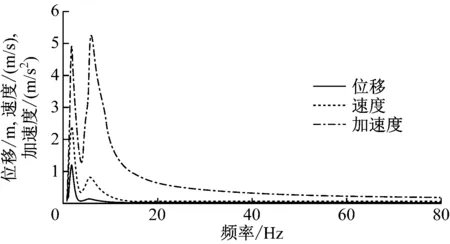
图2 车站楼板跨中位置谐响应分析图
由图2可知,楼板的振动敏感频率范围为0~20 Hz,其位移导纳、速度导纳、加速度导纳的变化趋势一致。谐响应分析在3.3 Hz附近第一次出现振动峰值,其结果与模态分析相符。
1.4 确定性列车荷载作用下结构振动响应分析
利用无砟轨道双层梁模型对轮轨力进行数值模拟,车轮动压力数值响应如图3所示。图3中,车轮动压力在量级上与多数文献结果相符,说明加载与计算方法均具有可靠性。
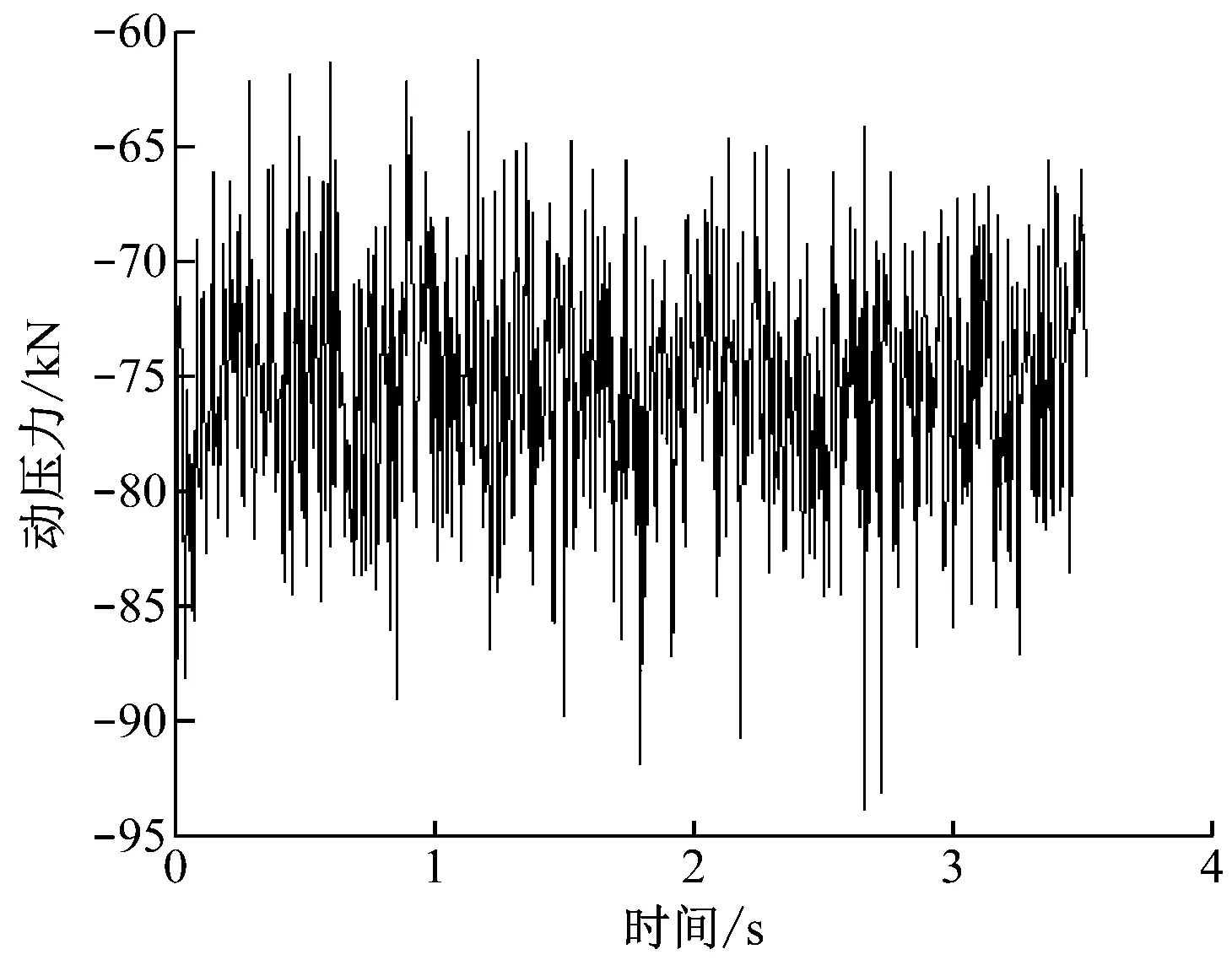
注:列车速度为180 km/h
本文所选取的具体线路布置如图4所示,具体工况详述如下。车站站台响应点如图5所示。
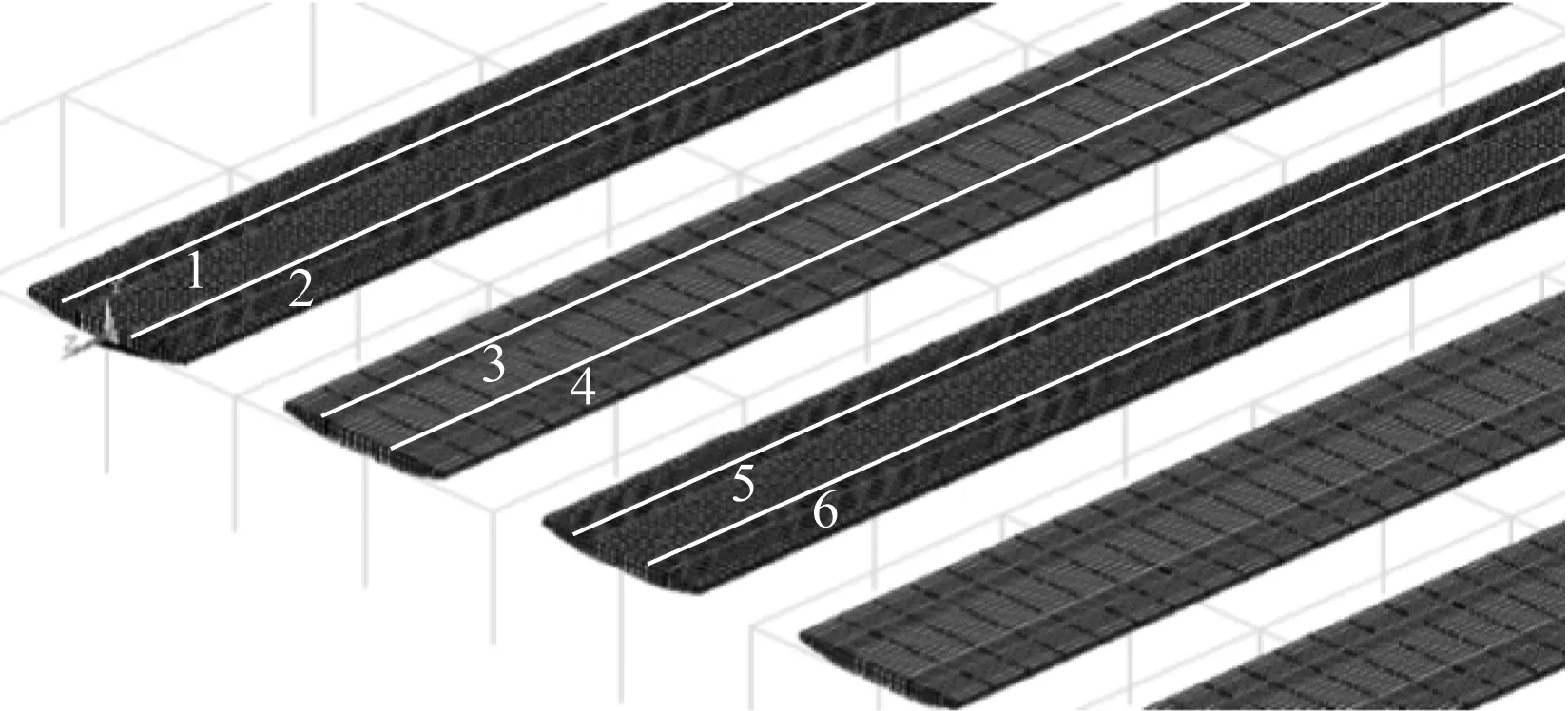
注:1、2、3、4均表示到发线;5、6均表示正线
(1) 工况1:线路1的列车以不同速度匀速通过枢纽车站,线路5的列车以不同速度匀速通过枢纽车站。
(2) 工况2:线路1的列车以240 km/h分通过枢纽车站,线路1、2的列车同时以240 km/h通过枢纽车站。
(3) 工况3:线路5的列车以240 km/h通过枢纽车站,线路5、6的列车以240 km/h通过枢纽车站。
(4) 工况4:线路6的列车以240 km/h通过枢纽车站,线路2的列车以240 km/h匀速通过枢纽车站。
(5) 工况5:4条相邻正线的列车以240 km/h匀速通过枢纽车站。
(6) 工况六6:不相邻到发线双线行车,即线路2、4的列车以240 km/h通过枢纽车站。
(7) 工况7:相邻到发线双线行车,即线路2、3的列车以240 km/h通过枢纽车站。
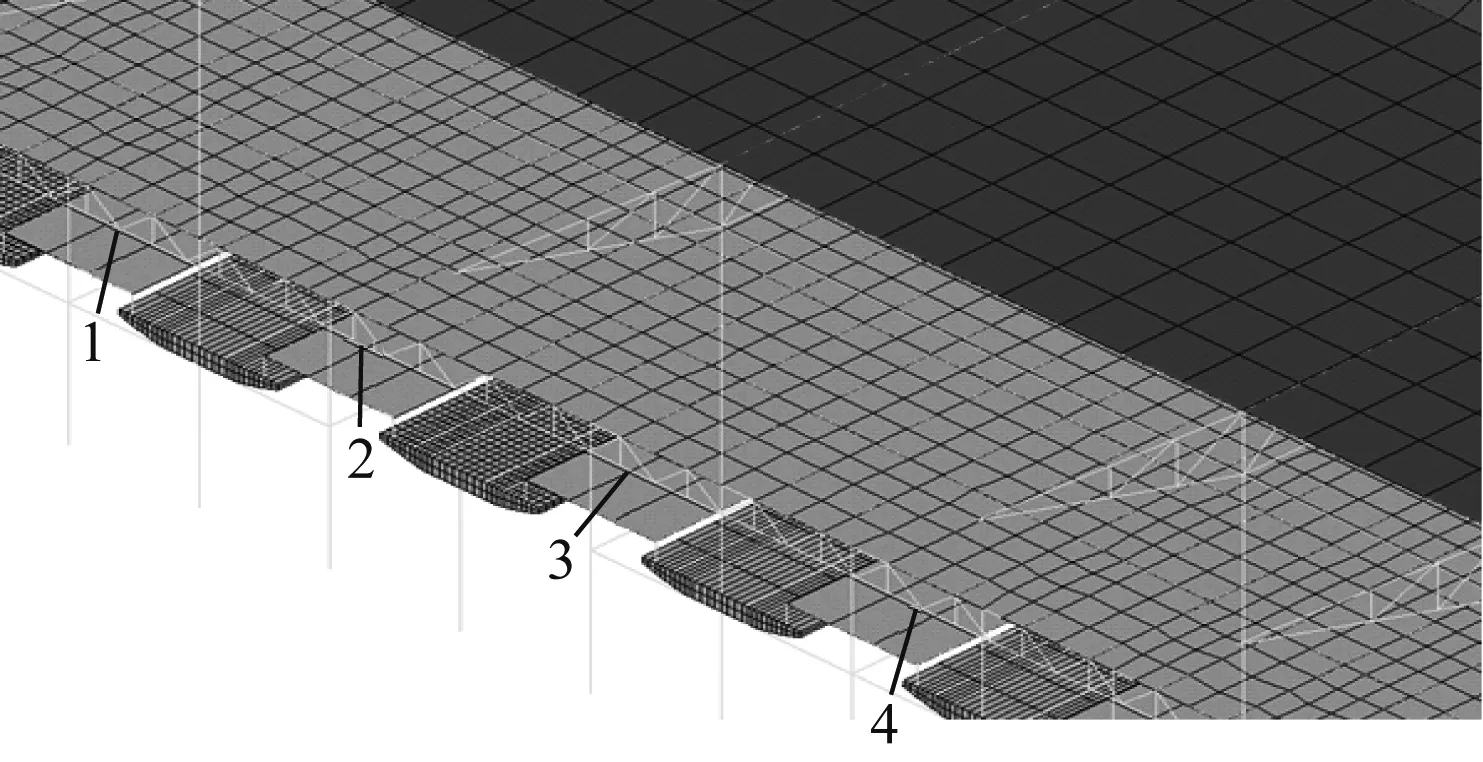
注:1、2、3、4表示4个站台的位置
1.4.1 不同列车工况下振动衰减规律
(1)到发线列车以不同行驶速度匀速通过南京南站时,不同结构层的竖向加速度响应如表2~3所示。
(2)正线列车以不同行驶速度通过南京南站时在不同结构层的竖向加速度响应如表4~5所示。

表2 到发线列车不同行驶速度时楼板结构的响应 cm/s2
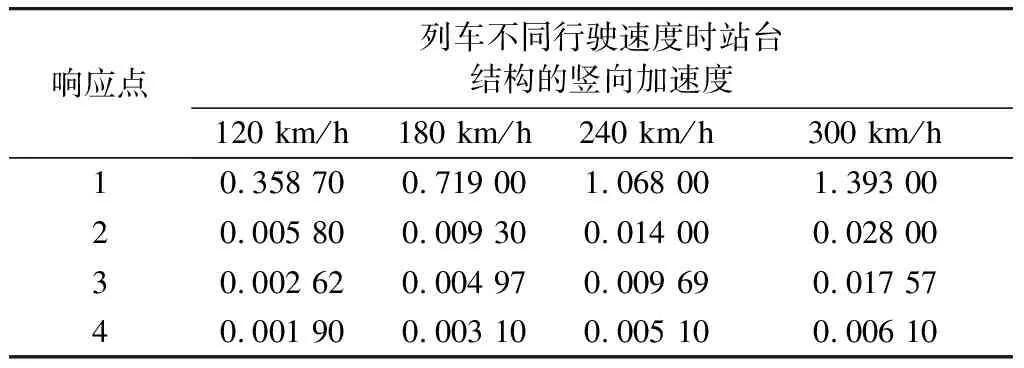
表3 到发线列车不同行驶速度时站台结构的响应 m/s2
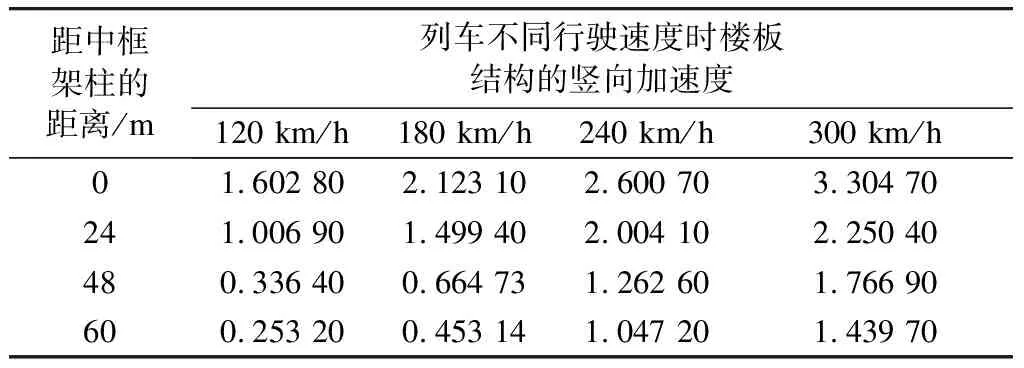
表4 正线列车不同行驶速度时楼板结构的响应 cm/s2
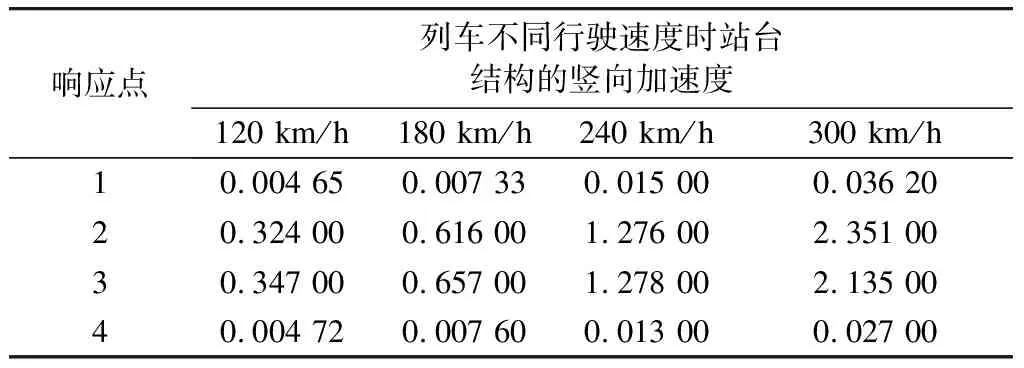
表5 正线列车不同行驶速度时站台结构的响应 m/s2
(3)正线列车、到发线列车以240 km/h在单、双线行车时,不同结构层的竖向加速度响应如表6所示。由表6可知:正线列车行驶工况对楼板的振动响应远小于到发线列车行驶引起的楼板振动响应。双线行车工况下,候车厅层楼板竖向加速度约为单线行车工况的两倍,正线列车由于无竖向支撑与上部结构连接,即使双线行驶,传递给上部结构的振动响应亦偏小。正线列车在不同的行驶速度下,楼板关键点在不同位置的衰减特性如图6~7所示。由图6~7可知,不同结构层的振动响应在水平方向离振源距离的增大呈现指数型衰减的趋势。
(4)不同工况下到发线的楼板关键点(关键点位于框架柱正上方的跨中楼板处)的振动响应如表7所示。由表7可知:正线列车由于间隔距离较远,激励叠加程度较小,竖向响应有所增加但程度不大;不相邻线路同时行车引起的振动响应并不是单独线路行车的2倍,说明相离线路之间的影响不大;相邻线路行车引起的车致振动对楼板层的振动响应有一定的影响。

表7 到发线列车不同行驶工况下楼板结构关键点的振动响应 cm/s2
1.4.2 柱网附近关键点的响应
当到发线列车以240 km/h的速度匀速通过南京南站时,可将柱网附近的响应采用图8直观表示。图8中,响应点1为中框架柱对应的楼板响应关键点,响应点2、3、4、5、6、7、8、9、10、11距中框架柱的水平距离分别为6 m、12 m、18 m、24 m、32 m、36 m、42 m、48 m、54 m、60 m。
通过图8可以直观地看出,随着距行车轨道中心线距离的增大,振动响应快速衰减,且位于相应楼板柱网附近的响应点,振动响应有所增加。
1.4.3 结构的振动衰减特性
选取南京南站有限元模型不同结构层的关键点进行分析,关键点的位置仅在高度方向有所差别。
当到发线列车以240 km/h的速度通过南京南站时,各结构层关键点在横向和竖向的振动响应如表8所示。衰减图像如图9所示。
由表8和图9可知,横向振动响应远小于竖向振动响应,且沿着车站高度的方向,车致振动呈指数衰减的趋势。
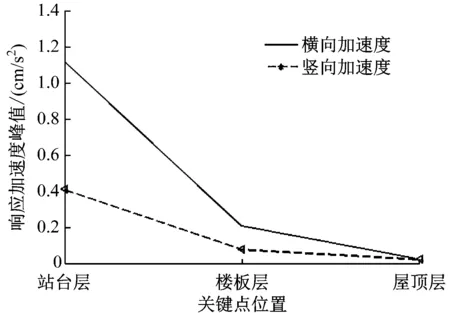
图9 关键点沿高度方向的衰减规律
2 振动水平评价
2.1 频谱分析
为了分析车站结构振动特性的传播规律,本文选取到发线列车以240 km/h的行驶速度通行南京南站时,对楼板层与站台层的响应进行频谱分析,如图10所示。
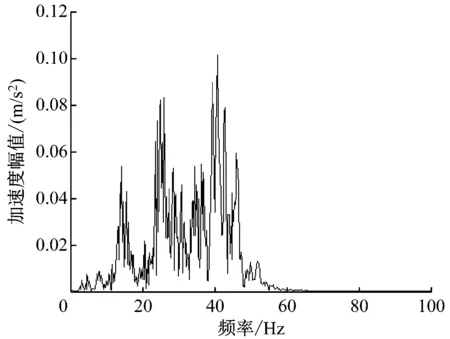
a) 站台层
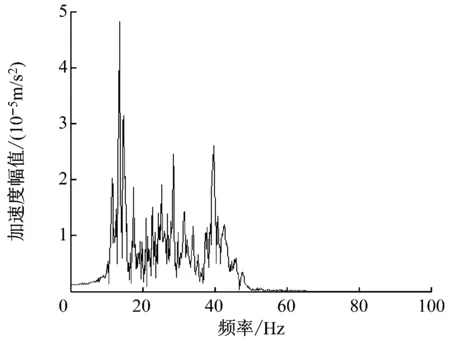
b) 楼板层
由图10可知,到发线列车在站台层的频谱特性较候车厅层丰富,站台层楼板的振动频谱为集中在1~60 Hz的低频振动,传至候车厅楼板时,频谱主要为集中在1~40 Hz的低频振动。
2.2 振动水平
为了分析列车通过时楼板振动水平在频域上的分布,对振动响应信号进行1/3倍频程分析,得到振级频谱曲线。
到发线列车以240 km/h的速度在单线线路上行驶时,站台层和候车厅楼板层的竖向加速度振级频谱如图11所示。
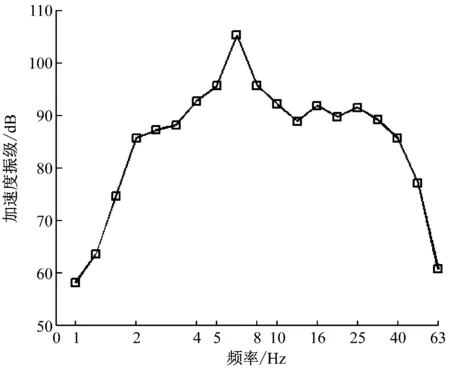
a) 站台层
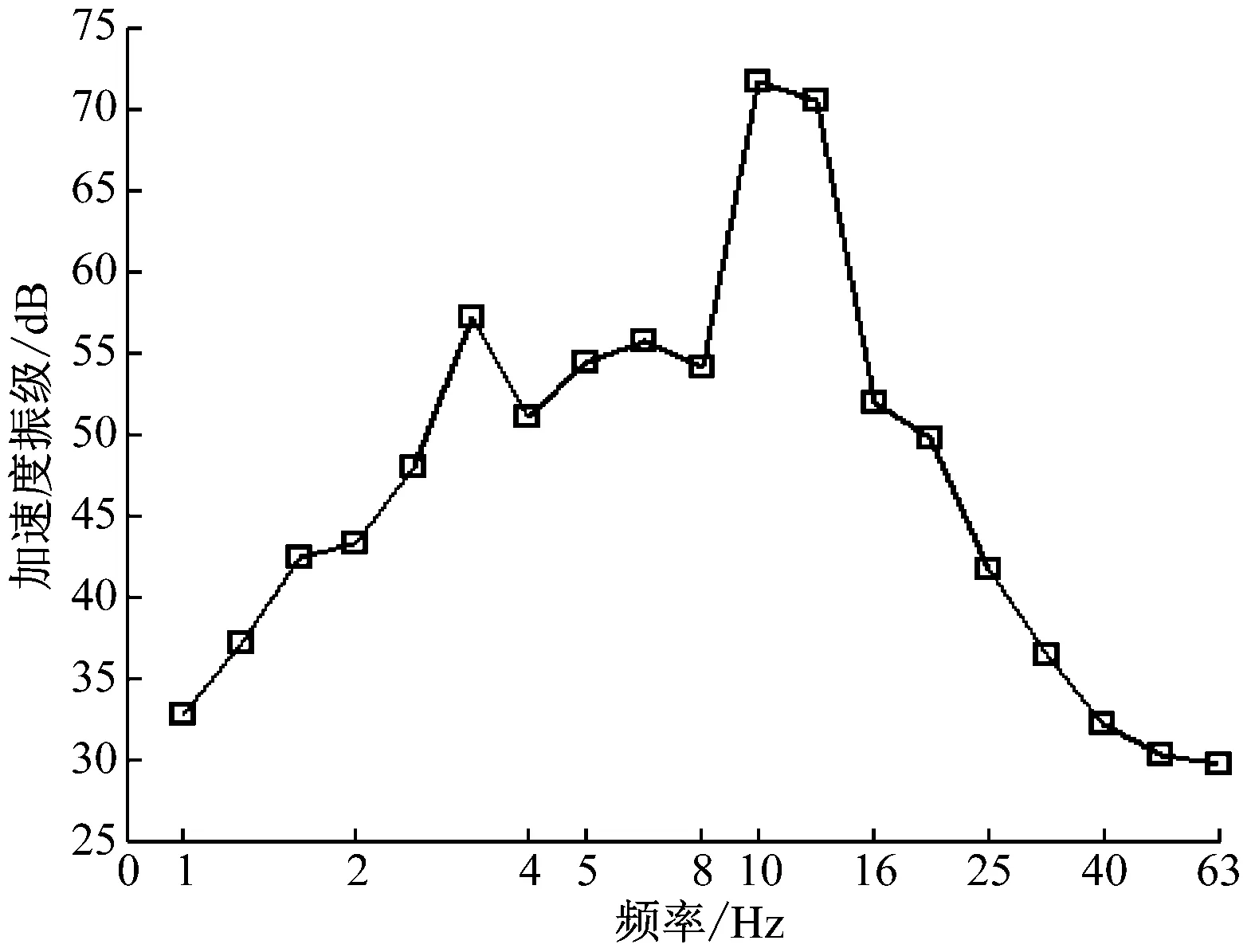
b) 楼板层
由图11可知,楼板在频率为3 Hz时,竖向振动加速度振级出现第一次峰值;而站台层楼板在频率为6.3 Hz时,竖向振动加速度振级出现第一次峰值。其最大的竖向加速度振级分别为72 dB和108 dB,这说明南京南站属于上柔下刚的结构体系;车致振动在竖向迅速衰减,与前面的研究基本吻合。
3 结论
(1)通过模态分析可以看出,南京南站属于上柔下刚的结构体系,楼板的一阶竖向自振频率与人行荷载的步行频率相接近,人致振动舒适度应该得到重视。
(2)选取关注的楼板关键点进行谐响应分析,楼板的卓越频率主要集中在0~10 Hz。
(3)正线列车的车致振动响应远小于到发线列车的车致振动响应。非相邻线路同时行车引起的振动响应并不是单独线路行车的2倍,非相邻线路之间的影响不大;相邻线路行车引起的车致振动对楼板层的振动响应存在一定的影响。
(4)南京南站各结构层关键点在横向振动响应远小于竖向振动响应。沿着楼层高度方向,车致振动呈现指数型衰减的趋势。距离行车轨道中心线不同距离处车致振动也呈现指数型衰减的趋势。
(5)研究了南京南站振源的传递特性,结果表明,由列车传至候车厅楼板的振动以0~40 Hz的低频振动为主,站台层的振动以0~60 Hz的低频振动为主,说明振动频谱中较高频率的成分沿着车站高度的方向迅速衰减。
