类矩形盾构隧道与圆形盾构隧道振动特性对比分析

2019-03-15张啟乐冯立力王建立

城市轨道交通研究 2019年3期

张啟乐冯立力王建立王建张斌

(1.隔而固(青岛)结构设计事务所有限公司，266108，青岛；2.宁波市轨道交通集团有限公司，315101，宁波//第一作者,工程师)

城市轨道交通在给人民群众的出行带来便利的同时，其运营过程中所诱发的环境振动及二次结构噪声问题对人们的影响亦越来越大。国际上已把环境振动列为七大环境公害之一，很多专家和学者对城市轨道交通振动的产生、传播及控制机理做了大量研究。

文献[1- 4]均仅限于对常规断面隧道振动特性及传递规律的研究，而针对异形盾构隧道,目前并未有任何公开的研究成果。

宁波地铁3号线一期工程首次采用类矩形盾构。该隧道为国内首条且为世界上最大的类矩形盾构隧道。本文以宁波地铁3号线一期工程为背景，对类矩形盾构隧道和圆形盾构隧道的振动特性进行对比分析。其结论可为宁波地铁4号线及后续城市线路规划及轨道结构设计提供参考。

1 钢轨振动荷载

目前,列车荷载的确定方法主要有模型分析法、经验分析法和试验分析法。本文基于试验分析法来获取钢轨振动荷载，即通过实测的钢轨振动加速度来反演得到钢轨振动荷载。

1.1 振动加速度数定

经小波分解和重构后的钢轨加速度时程可认为是一个具有零均值的各态历经的平稳高斯过程[5]，因此可以将钢轨振动加速度波形分解为一系列不同频率的谐波，即可用傅立叶级数表示为：

(1)

(2)

(3)

式中：

x(t)——钢轨加速度时程；

T——记录时长或截断时长；

N——加速度波形离散点的数量；

ω——基频，ω=2π/T。

对钢轨竖向振动加速度波形进行离散采样，即将加速度波形离散成单个点后得到：

(4)

1.2 钢轨振动荷载求解

将列车简化为一系、二系弹簧质量系统模型的组合[6]，并假定该组合沿隧道纵向均匀分布，简化模型如图1所示。假设列车车体重心在纵向、横向都是对称的，故在计算一侧钢轨上的列车荷载时，可只分析整车模型的1/4。

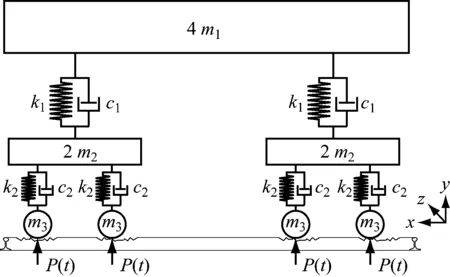
注:m1为1/4车体质量；m2为1/2转向架质量；m3为一个轴重质量；c1,k1为二系悬挂阻尼与刚度;c2,k2为一系悬挂阻尼与刚度；P(t)为轮轨接触力

根据图1 中的坐标系，选取简化列车模型的1/4为研究目标，利用直接平衡法建立车体竖向运动平衡方程为：

(5)

令y1-y0=ξ1,y2-y1=ξ2。经过推导可得：

(6)

式中：

g——重力加速度。

沿纵向均匀分布的列车线荷载F(t)可按照下式计算：

F(t)=KNMP(t)/L

(7)

式中:

K——修正系数；

N——每节车厢的转向架数量；

M——列车车厢数量；

L——列车长度。

宁波地铁车辆为B型车，则N取2，M取6，L取117.12 m。当K为1时，普通整体道床的轮轨振动荷载时程及频谱如图2～3所示。

图2 普通整体道床的轮轨振动荷载时程曲线

图3 普通整体道床的轮轨振动荷载频谱曲线

2 盾构隧道有限元模型建立

将隧道假定为平面问题进行有限元模型的建立。土层参数如表1所示，单元网格尺寸确定原则参见文献[7]。

模型中,土层和隧道衬砌结构等均采用PLANE 82单元。扣件采用Combine 14单元，扣件竖向刚度假定为33 kN/mm；钢轨仅考虑其单位长度上的质量，不考虑其弯曲和扭转变形，故钢轨采用Mass 21质量单元模拟。有限元模型横向长度为150 m，竖直方向长度为60 m。计算域边界采用人工粘弹性边界[8]。系统阻尼采用Rayleigh阻尼，其中α取3.94，β取1.25×10-4。

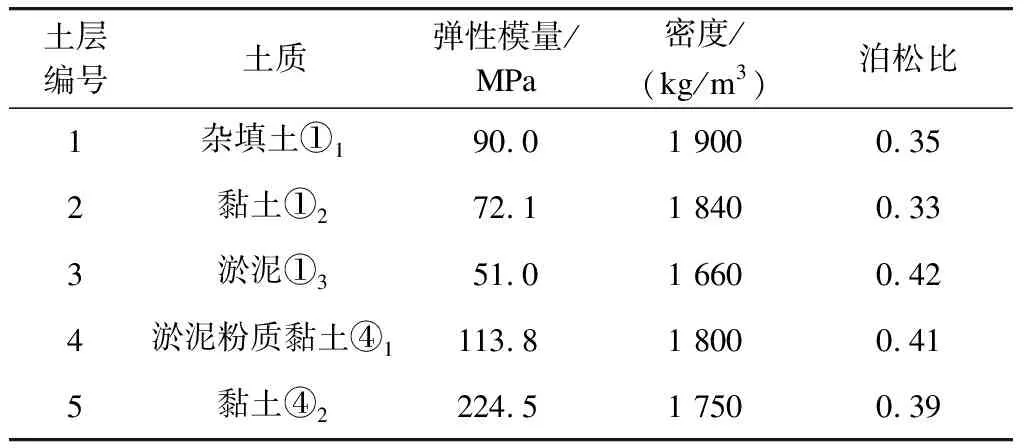
表1 土层参数表

3 两种盾构隧道计算结果分析

3.1 模态分析

分别建立单位长度的类矩形盾构和圆形盾构的管片模型，并对两种模型进行模态分析，计算结果如图4所示。

图4 盾构管片振型

由图4可知，类矩形盾构管片的竖向敏感频率为127 Hz，圆形盾构管片的竖向敏感频率为82 Hz，由此可知,类矩形盾构管片的敏感频率相对圆形盾构管片更高。由轮轨振动荷载频谱图(见图3)可知，轮轨振动的能量主要集中在50～80 Hz，与普通圆形盾构管片相比，类矩形盾构管片的自振频率与轮轨振动的卓越频率重叠区域更小，这对控制隧道管片结构的共振更为有利。

3.2 两种盾构隧道结构相同位置振动特性对比

选取类矩形盾构隧道和圆形盾构隧道的道床中心、隧道壁(距离轨面1.25 m)及线路正上方地面点作为振动输出点，对比两种隧道结构的振动加速度及1/3倍频程加速度级。

3.2.1 振动加速度

两种盾构隧道振动加速度峰值对比如表2所示。由表2可知，圆形盾构隧道的振动要大于类矩形盾构隧道;在道床位置，两种隧道振动差别最大，圆形盾构隧道道床振动加速度峰值比类矩形盾构隧道大2.32 m/s2；在线路正上方地面位置两者差别相对较小，圆形盾构隧道道床振动加速度峰值比类矩形盾构隧道大0.072 m/s2。这是由于与圆形盾构隧道相比，类矩形盾构隧道断面更大，因而其质量和整体刚度均较大，在相同振动荷载作用下更不容易被激振，所以类矩形盾构隧道的振动相对较小。

表2 振动加速度峰值对比 m/s2

3.2.2 振动加速度级

1/3倍频程谱是一种频域分析方法，具有谱线少、频带宽的特点。两种盾构隧道的道床、隧道壁和线路正上方地面点的振动加速度级,如图5所示。

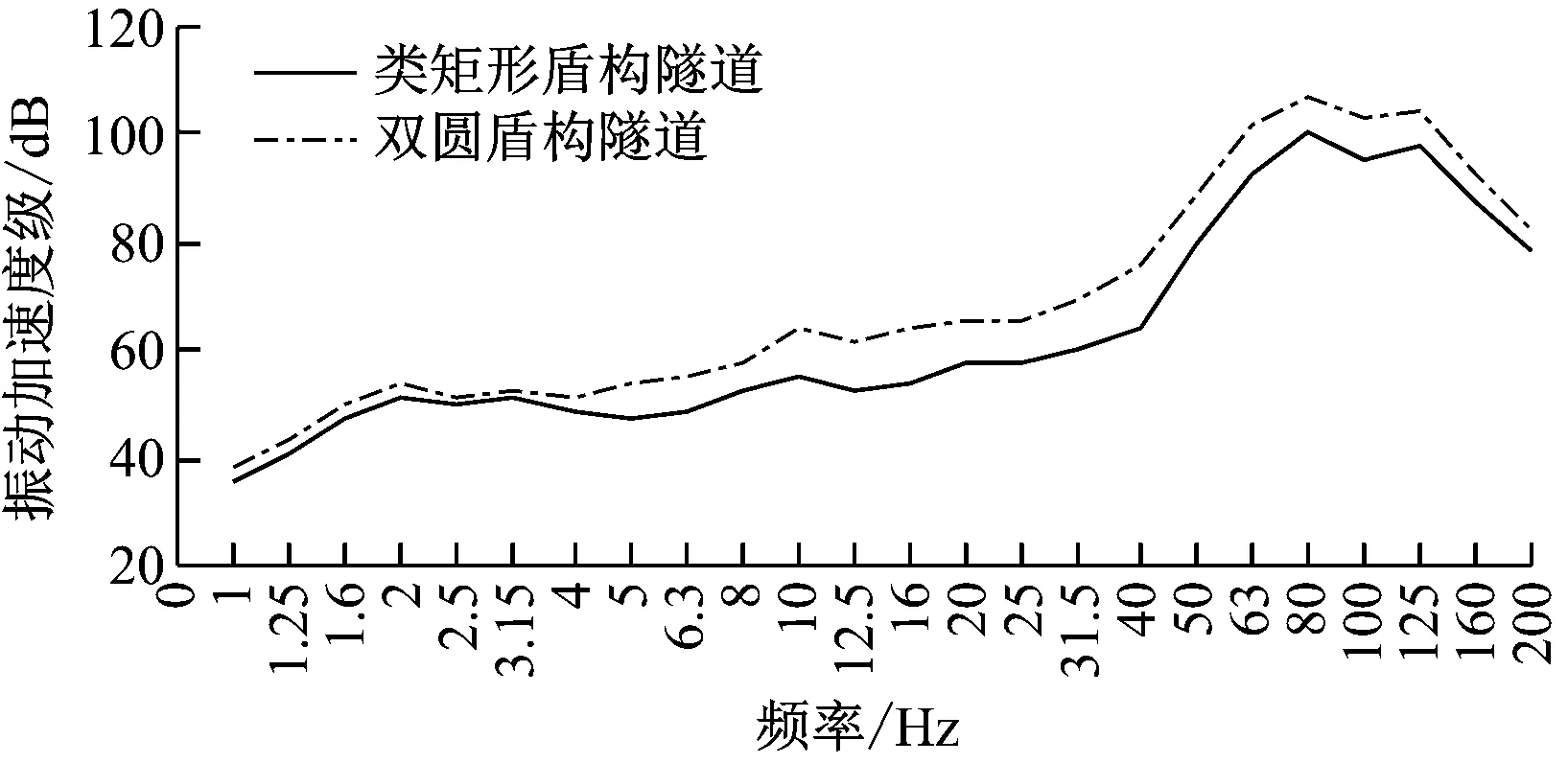
图5 道床中心振动加速度级

图6 隧道壁振动加速度级

图7 线路正上方地面振动加速度级

由图5～7可知，在道床中心位置，圆形盾构隧道与类矩形盾构隧道在频域内的振动特性几乎一致，频率为50 Hz以下时轮轨振动较小，振动较大的频段集中在63～80 Hz，这与轮轨振动荷载的主频一致。同时可以发现,两种隧道轮轨振动荷载均在80 Hz达到最大值，类矩形盾构隧道振动加速度级最大值为104 dB，圆形盾构隧道振动加速度级最大值为112 dB，圆形盾构隧道要比类矩形盾构隧道大8 dB，圆形盾构隧道的振动加速度级在大部分频段均大于类矩形盾构隧道。

在隧道壁位置，两种隧道的振动加速度级同时在63 Hz处达到最大值，类矩形盾构隧道振动加速度级最大值为94.2 dB，圆形盾构隧道振动加速度级最大值为97.5 dB，圆形盾构隧道要比类矩形盾构隧道大3.3 dB；两种隧道在100 Hz时的振动加速度级差值最大，圆形盾构隧道比类矩形盾构隧道大16.23 dB；在10 Hz以下的低频区间，两种隧道的振动水平差别不是很明显。

在线路正上方地面位置，对于4～20 Hz的振动，类矩形盾构隧道略大于圆形盾构隧道；对于25～63 Hz的振动，圆形盾构隧道要大于类矩形盾构隧道。

由此可见，隧道内部不同位置及隧道内外的振动在频域内的特性都是不同的。隧道内部不同位置的振动特性差异主要是由隧道结构局部模态与轮轨荷载的共振导致；而隧道内外的振动特性差异是由于振动经过土层的滤波，某些频率的振动出现不同程度的衰减而导致的。

3.2.3 振动加速度级传递损失

图8为隧道壁到线路正上方地面的振动加速度级传递损失。由图8可知，对于低频振动，两种隧道的传递损失几乎相同，即虽然两隧道结构形式不同，但是低频振动衰减规律却一致；无论圆形盾构隧道还是类矩形盾构隧道，均呈现出振动频率越高，传递损失越大的趋势。但是对于80～200 Hz的高频振动，圆形盾构隧道的传递损失明显要大于类矩形盾构隧道。这是因为圆形盾构隧道质量较轻，列车经过时更能激发高频振动，而高频振动衰减较快，所以圆形盾构隧道的传递损失较大。

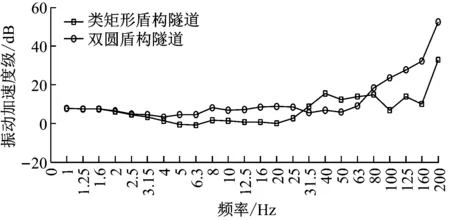
图8 隧道壁到线路正上地面的传递损失

3.2.4 Z振级

圆形盾构隧道与类矩形盾构隧道在道床、隧道壁与线路正上方地面位置的Z振级如表3所示。

表3 各计算点Z振级 dB

由表3可知，圆形盾构隧道道床中心位置Z振级要比类矩形盾构隧道大7.2 dB；圆形盾构隧道壁Z振级比类矩形盾构隧道大1.7 dB；线路正上方地面位置，圆形盾构隧道Z振级比类矩形盾构隧道大1.2 dB。

3.3 考虑选线因素的环境振动对比

与圆形盾构隧道相比，类矩形盾构隧道在进行规划选线时具有更强的灵活性。表4为两种隧道的选线对比。

表4 两种隧道的选线对比

选择圆形盾构隧道右线正上方地面作为振动评价点，计算评价点的Z振级见表5。

表5 计算点Z振级对比表 dB

由表5可知，如果隧道采用类矩形盾构，且按照工况1进行选线，则由地铁运行引起的评价点的振动为65.2 dB，该值要比圆形盾构隧道环境振动小4.0 dB；如果按照工况2进行选线，则由地铁运行引起的评价点的振动为62.1 dB，该值要比圆形盾构隧道环境振动小6.9 dB。由此可知，类矩形盾构隧道的特殊断面形式使选线更灵活，从而减轻了对地铁环境振动的干扰。

绘制两种选线工况振动评价点的1/3倍频程振动加速度级，见图9～10。

图9 选线对比工况1时1/3倍频程振动加速度级

图10 选线对比工况2时1/3倍频程振动加速度级

由图9～10可以发现，无论按照工况1还是工况2进行选线，与圆形盾构隧道比较，类矩形盾构隧道振动频率降低了20～120 Hz，且在50～80 Hz降低较为明显。研究发现，地铁振动二次结构噪声频率范围一般为20～200 Hz，且峰值一般出现在50～80 Hz，1/3倍频程加速度级为35～45 dB[ 10-11]。由此可见,如果采用类矩形盾构隧道，且按照工况1或者工况2选线，将会降低建筑二次结构噪声。而二次结构噪声和建筑结构的局部模态相关，因此二次结构噪声量的降低值，应根据具体的建筑结构形式进行计算。