神经网络技术在柴油加氢精制装置生产中的应用
2019-03-15刘亚利
肖 强,刘亚利,国 庆
(中海油石化工程有限公司,山东 青岛 266101)
随着人们生活水平的提高,国内汽车保有量也在急速增加。柴油由于具有挥发度低、经济性好、着火点高、使用安全、稳定性好等特点,备受消费者关注。但是柴油车尾气污染问题却在不断加重,柴油燃烧产生的硫氧化物能够造成严重的大气污染,因而车用柴油的硫含量问题日益受到关注。根据国家标准GB 19147—2016的规定,从2017年1月1日起,全国范围内需实施车用柴油国Ⅴ标准,柴油硫质量分数要求不大于10 μg/g。因此,国内石化企业必须按照标准要求,进行柴油加氢精制装置的升级改造和先进控制优化,以生产符合标准的柴油产品,实现良好的生产效益。
国内某石化企业为生产符合国Ⅴ标准的柴油,2017年底完成了对1.0 Mt/a柴油加氢精制装置的改造升级,并于2018年初开车运行。为了使新生产工艺能够达到先进控制和在线优化,以达到节能降耗和提高生产效益的目的,有必要建立一个能够预测柴油加氢反应系统工艺条件或者柴油产品硫含量的模型。文献[1-2]报道的反应动力学模型虽能较好地模拟柴油馏分加氢反应过程,但准确度较低,因此考虑采用人工神经网络技术进行建模。
作为一种黑箱模型,人工神经网络可以忽略过程机理,通过模拟过程的输入与输出之间的关系,达到对系统的建模。周轶峰等[3]采用实验室平台数据,应用人工神经网络方法建立了用于柴油馏分加氢脱硫反应的预测模型,取得了良好的预测效果。但是基于工业实际生产数据的研究尚未见报道。本研究基于国内某石化企业1.0 Mt/a柴油加氢精制装置的实际生产数据,采用人工神经网络建立能够预测柴油加氢产品硫含量的模型,用于指导装置生产操作。
1 装置概况
国内某石化企业1.0 Mt/a柴油加氢精制装置加氢反应系统原有1台加氢精制反应器,2017年底经过改造后,新增1台加氢精制反应器,新增加氢反应器与原反应器串联运行,加氢反应系统流程示意如图1所示。原料柴油与循环氢混合后,经加热炉升温后依次进入反应器R-101和R-102进行催化加氢精制反应,最终得到加氢精制柴油。两台反应器内部各有3段床层,通过急冷氢控制各段床层的反应温度。
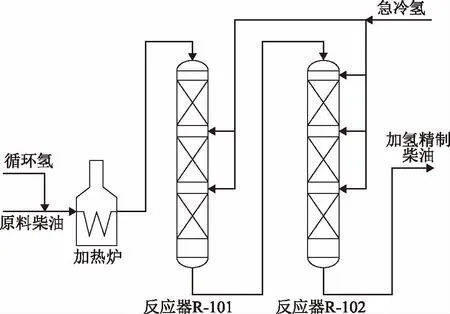
图1 加氢反应系统流程示意
该套装置的原料由厂区直馏柴油、焦化柴油和催化裂化柴油混合而来,2018年1月2日开车运行,开始生产符合国Ⅴ标准的柴油。收集2018年1月5日至5月31日生产工艺数据,筛选出生产过程中对加氢脱硫反应影响较大的工艺参数,最终确定了140组生产数据。产品柴油的硫含量不仅与原料柴油的性质有关,还与加氢反应工艺条件有关。部分原料柴油的性质如表1所示。不同工艺条件下的加氢精制柴油产品性质如表2所示。根据文献[4-6]的研究结果和模型本身的性能优势,动量BP神经网络、LMBP神经网络和RBF神经网络在化工过程中均有良好的预测效果。因此本研究应用采集的数据,分别采用上述3种神经网络技术对柴油加氢反应系统进行建模,考察用于预测柴油加氢产品硫含量的最佳模型。
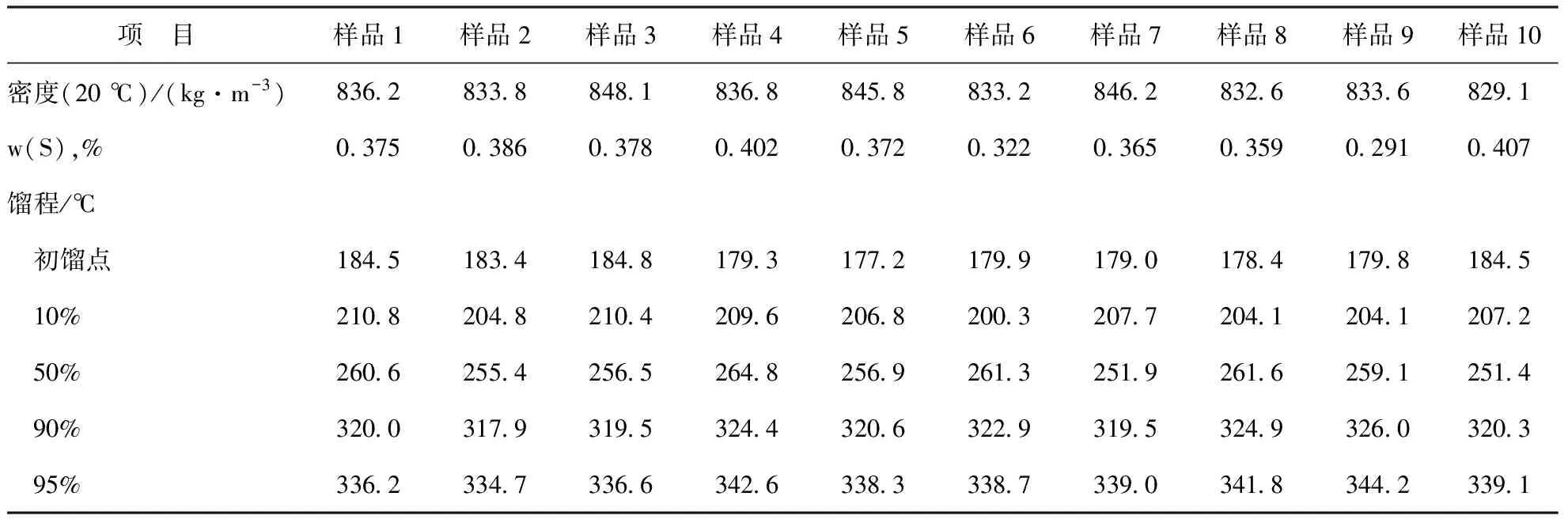
表1 部分原料柴油的性质
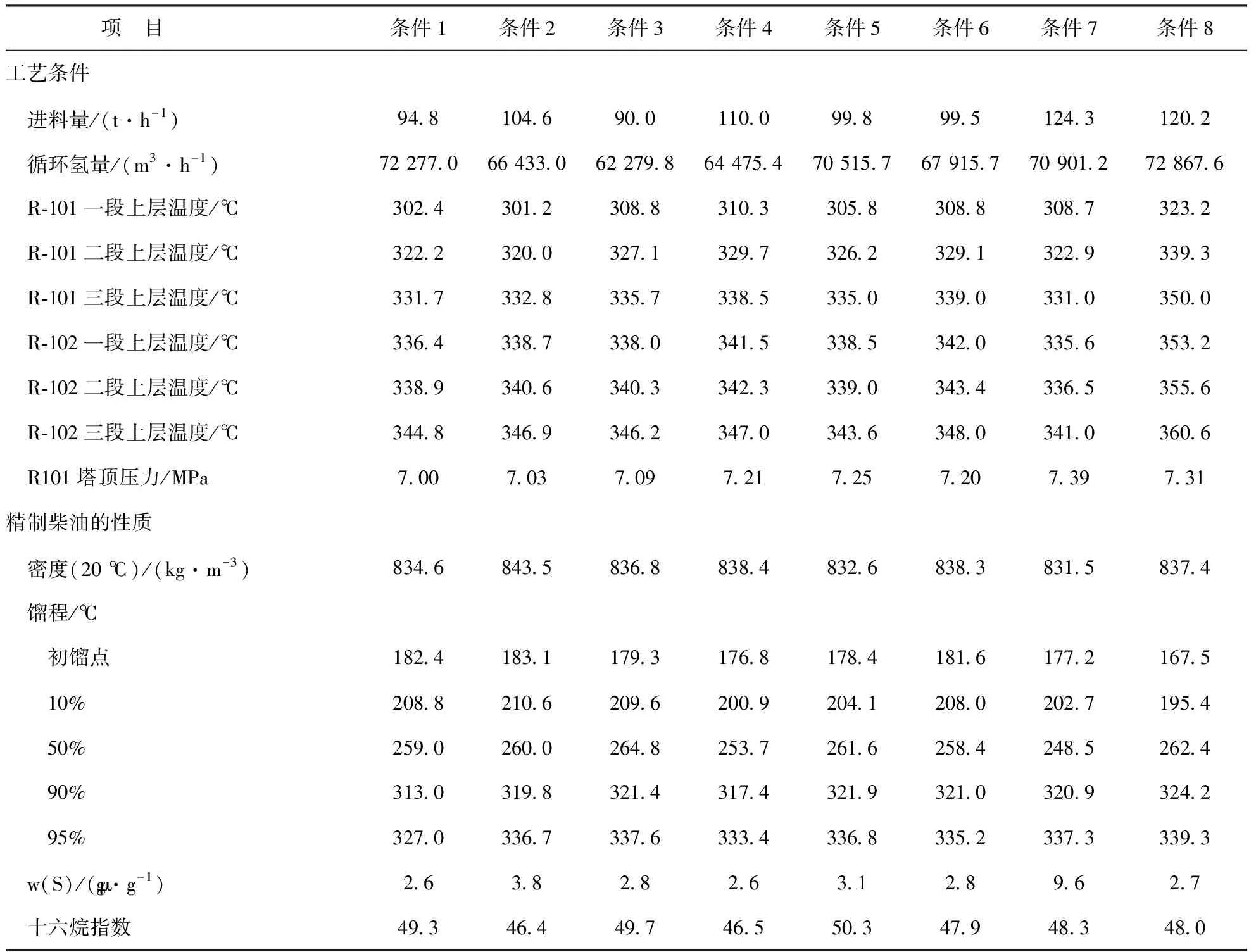
表2 不同工艺条件下精制柴油的性质
2 模型的建立
人工神经网络通常由输入层、隐层和输出层3层构成,能否采用人工神经网络建立准确的用于预测柴油产品硫含量的模型,模型输入层的确立至关重要。柴油产品硫含量主要受原料柴油性质和加氢反应工艺条件决定。实际生产中,原料柴油硫含量、95%馏出温度、密度、进料量、循环氢量、R-101一段上层温度、R-101二段上层温度、R-101三段上层温度、R-102一段上层温度、R-102二段上层温度、R-102三段上层温度、R101塔顶压力共12个变量对柴油加氢脱硫影响较大。因此选择这12个变量作为输入层,同时,使用产品柴油硫含量这一单一变量作为输出层建立模型。
MATLAB软件中含有神经网络工具箱系统,它为神经网络的应用设计、分析、计算等提供了极大的方便。因此,本研究选择使用MATLAB2016a编程建立预测柴油产品硫含量的人工神经网络模型。
2.1 动量BP神经网络的建立
BP神经网络通常采用启发式学习算法进行改进,以克服收敛速度慢、局部极值难以确定的问题[7-10]。动量BP算法作为一种启发式学习算法,对表现函数梯度加以分析,从而改进了算法。
2.1.1网络隐层神经元数的确定动量BP神经网络模型的结构方面关键是确定隐层神经元数,通过设定相同训练次数(8 000次)和学习速率(0.4),改变隐层神经元数,进行训练,不同隐层神经元数的神经网络的训练误差结果见表3。可以确定最佳隐层神经元数为7,因此建立用于预测柴油产品硫含量的12×7×1单隐层动量BP神经网络。

表3 不同隐层神经元数的神经网络的训练误差
2.1.2网络的训练将筛选出的140组生产数据分为两组,随机选出120组数据作为训练集,其余20组数据作为预测集。采用MTALAB2016a进行编程,调用神经网络工具箱中的newff函数建立网络。对动量BP网络的参数进行设置,学习速率设为0.4,动量因子设为0.8,最大迭代次数设为8 000,最大迭代误差为0.001,输入层与隐层以及隐层与输出层之间的传递函数均选择sigmoid型函数中的tansig。将训练集120组数据归一化后,首先对动量BP神经网络进行训练,训练结果见图2。由图2可以看出,训练结果较好,模型的参数设置较为理想。
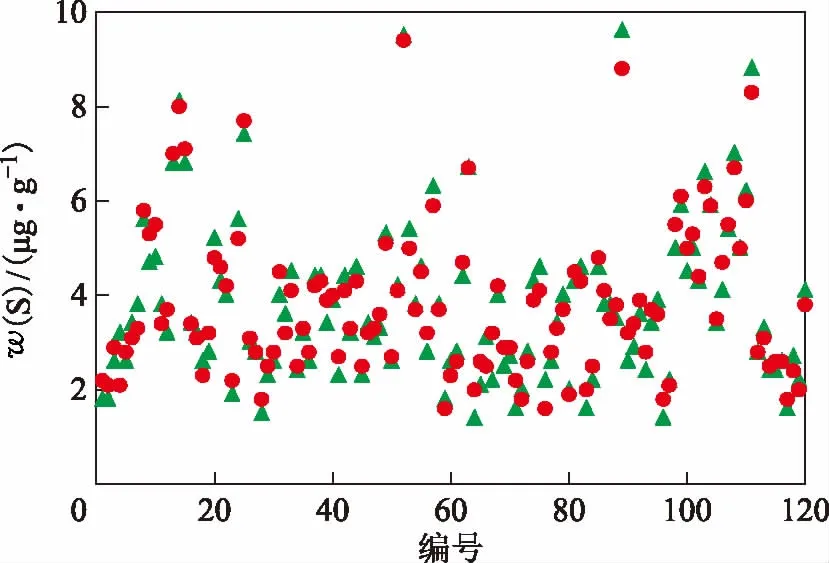
图2 动量BP神经网络对柴油产品硫含量的训练结果●—预测值; ▲—实际值。图3、图4同
2.1.3网络的预测通过调用sim函数对预测集20组数据进行仿真预测,然后应用postmnmx函数完成对数据的反归一化,得到预测结果。预测结果与实际值的偏差见表4。由表4可以看出,20组数据中预测值与实际值的最大相对偏差为6.67%,最小相对偏差为0.95%,平均相对偏差为3.50%,表明所建立的动量BP神经网络对柴油产品硫含量的预测性能较好。

表4 动量BP神经网络对柴油产品硫含量的预测结果
2.2 LMBP神经网络的建立
LM算法是应用Levenberg-Marquardt方法对BP算法进行的改进。该方法的引入能使BP算法在以近似二阶的训练速率进行修正时,避免计算Hessian矩阵,使过程避免复杂化,从而加快BP神经网络的训练速度,提高训练精度[11-12]。
2.2.1网络隐层神经元数的确定通过设定相同训练次数(500次),改变隐层神经元数,进行训练,不同隐层神经元数的神经网络的训练误差结果见表5。可以确定最佳隐层神经元数为8,因此建立用于预测柴油产品硫含量的12×8×1单隐层动量BP神经网络。

表5 不同隐层神经元数的神经网络的训练误差
2.2.2网络的训练与动量BP神经网络建立时相同,将随机选出的120组数据作为训练集,其余20组数据作为预测集。采用MTALAB2016a神经网络工具箱中的newff函数建立网络,调用trainlm函数建立LMBP神经网络。对网络的参数进行设置,最大迭代次数设为500,最大迭代误差为0.001,输入层与隐层之间的传递函数选为tansig,隐层与输出层之间的传递函数选为purelin。将训练集120组数据归一化后,首先对LMBP神经网络进行训练,训练结果见图3。由图3可以看出,训练结果较好,模型的参数设置较为理想。
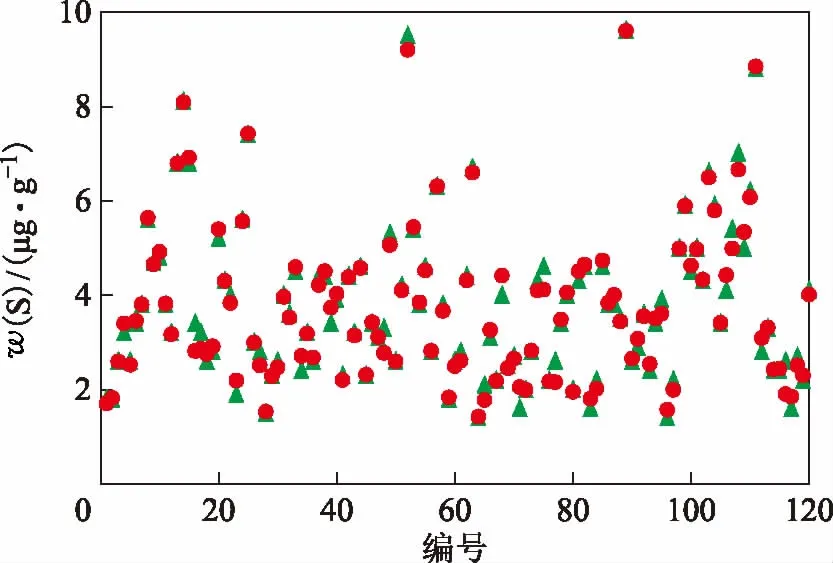
图3 LMBP神经网络对柴油产品硫含量的训练结果
2.2.3网络的预测调用sim函数对预测集20组数据进行仿真预测,然后应用postmnmx函数完成对数据的反归一化,得到预测结果。预测结果与实际值的偏差见表6。由表6可以看出,20组数据中预测值与实际值的最大相对偏差为4.32%,最小相对偏差为-0.51%,平均相对偏差为2.30%。表明所建立的LMBP神经网络对柴油产品硫含量的预测精度较高。
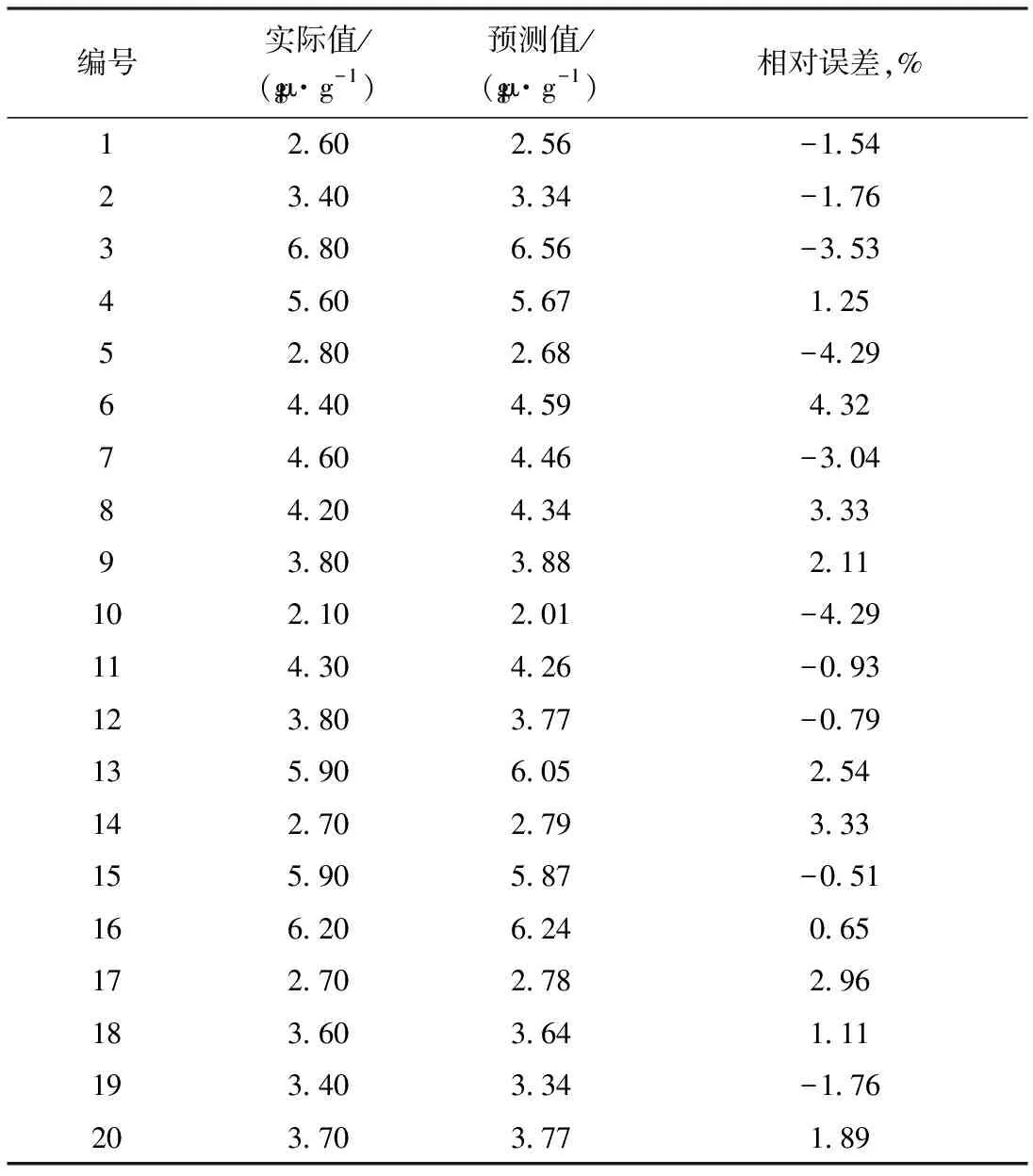
表6 LMBP神经网络对柴油产品硫含量的预测结果
2.3 RBF神经网络的建立
RBF神经网络即径向基函数神经网络,它是在高维空间进行差值的一种技术,RBF作为一种局部逼近的神经网络,在逼近能力、分类能力和学习速度等方面更具优势[13-14]。
2.3.1网络结构的确定在RBF神经网络模型的建立过程中,最重要的是径向基函数的分布常数spread的选取,spread值的选取决定了模型的运算性能和预测精度。因此,选取不同的spread值,对训练误差进行考察,结果见表7。由表7可以看出,当spread为1.80时,网络的均方误差最小,所以spread值选定为1.80。
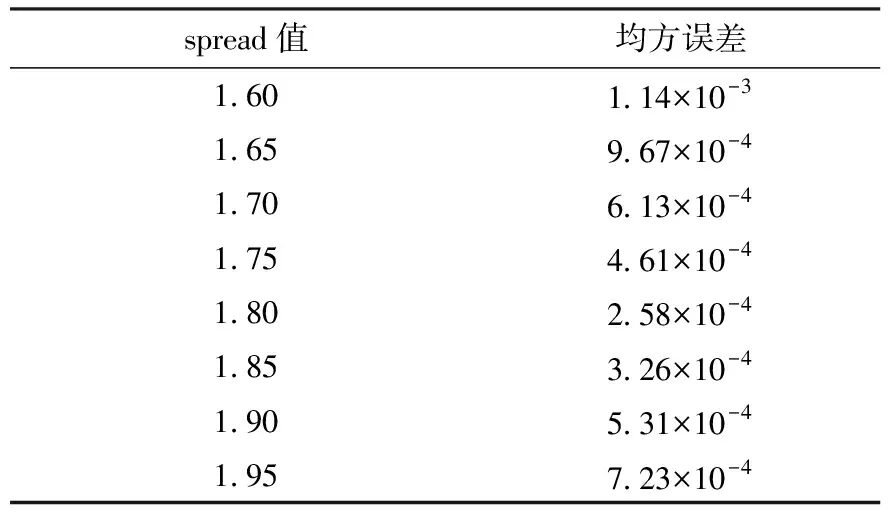
表7 不同spread值对应的均方误差
2.3.2网络的训练与前两种神经网络建立时相同,将随机选出的120组数据作为训练集,其余20组数据作为预测集。通过调用newrb函数建立RBF神经网络模型。对各项参数进行设定,spread值为1.80,训练精度设为0.001,隐层最大神经元数为100,每次训练增加的神经元数为1。对预测集的120组数据进行训练。前120组数据训练结果如图4所示。由图4可以看出,训练结果较好,参数设置理想。
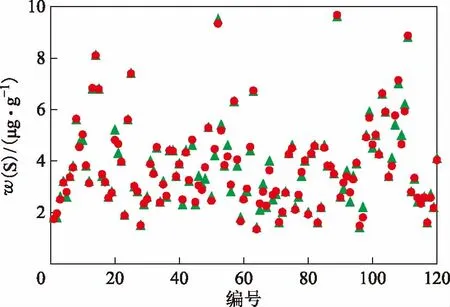
图4 RBF神经网络对柴油产品硫含量的训练结果
2.3.3网络的预测调用MATLAB2016a中的sim函数对预测集20组数据进行仿真预测,应用postmnmx函数完成模拟数据的反归一化,得到预测结果。预测结果与实际值的对比见表8。20组数据中预测值与实际值的最大相对偏差为5.00%,最小相对偏差为0.17%,平均相对偏差为2.18%。表明所建立的RBF神经网络对柴油产品硫含量的预测精度较高。
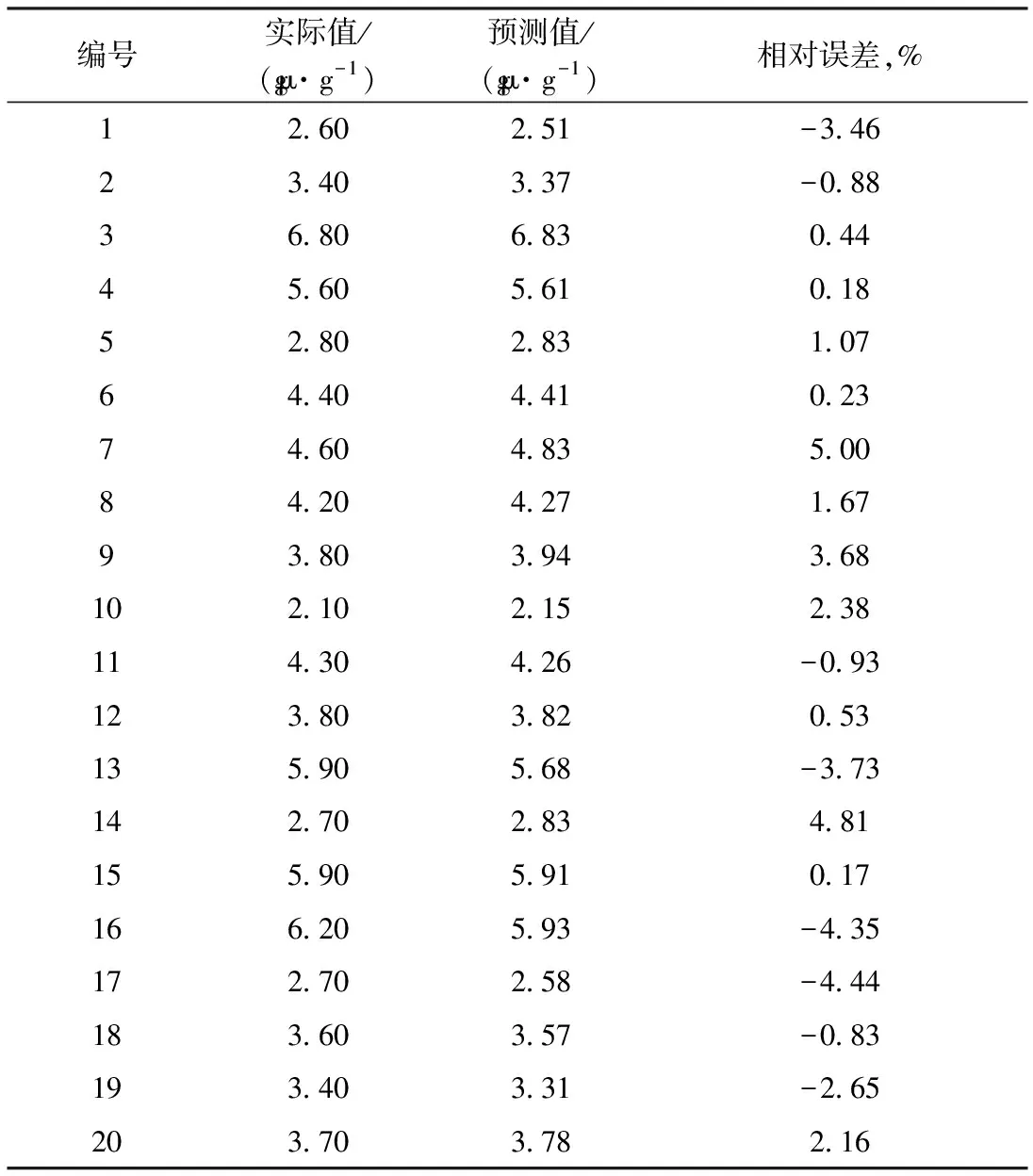
表8 RBF神经网络对柴油产品硫含量的预测结果
2.4 3种神经网络的对比
通过以上对3种模型的分析可以看出,使用动量BP神经网络、LMBP神经网络和RBF神经网络均能够成功地建立起预测柴油加氢产品硫含量的模型。3种人工神经网络对产品柴油硫含量预测的平均相对误差分别为3.50%,2.30%,2.18%,均小于5%,预测效果较好,能够达到工业预测的要求。但是通过对比可以看出,RBF神经网络对产品柴油硫含量预测的平均相对误差最小,其预测性能是3种人工神经网络中最佳的,因此,最终选用RBF神经网络作为该套柴油加氢精制装置的预测模型。
3 模型泛化能力的确定
泛化能力体现了人工神经网络用于对未知数据预测的性能。已建立的神经网络模型是基于已收集的生产操作数据,但是实际生产过程中再现已有的生产数据是不可能的,而且未来的生产数据还可能超出已有数据所覆盖的范围。因此,为了使用人工神经网络更准确地指导生产操作,必须对人工神经网络的泛化能力进行检验。
原料柴油的硫含量高低直接决定了油品中硫的脱除难易程度,原料柴油硫含量越高,脱硫难度相对越大。因此,为了检验所建立RBF神经网络的泛化能力,以原料柴油硫含量为例进行考察。
采集2018年6月3日至6月27日的生产数据,筛选出20组生产数据,该20组数据中原料柴油硫质量分数界于0.412%~0.430%之间,而原训练集生产数据中原料柴油硫质量分数介于0.291%~0.407%之间。同时,其他神经网络输入变量均在原训练集数据覆盖范围以内。
将筛选出的20组生产数据代入原RBF神经网络中,通过RBF神经网络进行仿真预测,得到预测数据与实际数据的对比结果,如表9所示。由表9可以看出,硫含量的预测值与实际值的相对误差最大为-6.67%,平均相对误差达到3.79%。预测值与实际值的平均相对误差小于5%,在工业要求的误差范围内,说明该模型对原料柴油产品硫含量具有较好的泛化能力。
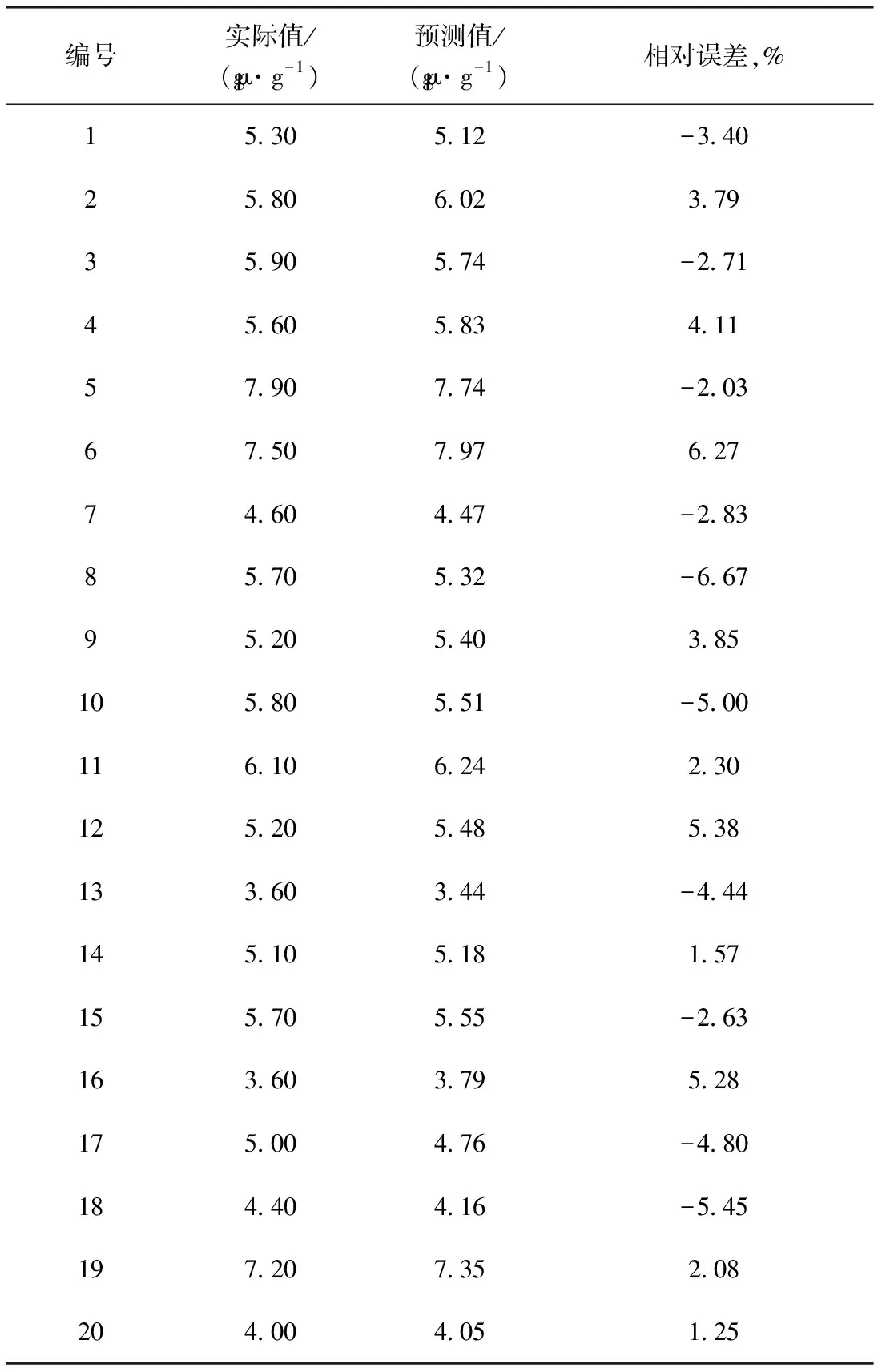
表9 另取20组柴油产品的硫含量预测结果
4 结 论
(1)分别应用动量BP神经网络、LMBP神经网络和RBF神经网络为国内某石化企业1.0 Mt/a柴油加氢精制装置建立用于预测柴油加氢产品硫含量的模型,有利于优化指导生产,保证柴油产品合格,达到国Ⅴ柴油标准。
(2)动量BP神经网络、LMBP神经网络和RBF神经网络对柴油加氢产品硫含量预测的平均相对误差分别为3.50%,2.30%,2.18%,RBF神经网络的预测性能最佳,最终选定RBF神经网络作为该套柴油加氢精制装置的预测模型。
(3)通过原料柴油硫含量对所建RBF神经网络的泛化能力进行了考察,结果表明模型的泛化能力较强,具有良好的适应能力。
(4)所建RBF神经网络模型对柴油产品硫含量具有较好的预测能力,可以对该套柴油加氢精制装置反应系统进行先进控制和在线优化。
