深基坑开挖对临近既有地铁隧道的纵向影响分析

裴 行 凯

(广州地铁设计研究院股份有限公司， 广东 广州 510010)

随着地铁沿线地块开发的日益增多，深大基坑对临近运营中的地铁隧道影响与保护成为工程关注和研究的重点。目前，利用数值模拟研究基坑开挖对地铁隧道的影响是进行工程评估和研究的主要手段[1-6]。

文献[7-8] 通过在临地基坑的地铁隧道上进行自动化监测和数值模拟的对比，分析了基坑开挖对临近隧道位移和变形的影响趋势。文献[9-10]结合现场实测数据分析，研究了基坑开挖整个施工过程中隧道变形的发展轨迹，并针对不同阶段提出了相应的控制措施。文献[11-13]对于地铁隧道正上方基坑开挖的保护措施进行数值分析，锯齿状连续墙结构可以起到有效的抑制土体隆起的作用，进而减少了对地铁隧道的影响。文献[14]利用简化理论计算方法和数值模拟联合，研究了上海某基坑工程对地铁的影响，并将分析结果与现场实测进行对比，隧道的变形规律基本吻合。

本文基于软土地区基坑开挖对地铁隧道影响的数值模型，着重分析受基坑开挖影响的隧道纵向衬砌断面应力和弯矩分布规律，为后续工程的设计施工提供明确的理论和计算依据。

1 模型的建立

结合已有工程实例，拟建一基本分析模型，该模型中考虑基坑平面尺寸为长方形，取基坑开挖尺寸为 26 m×40 m，考虑对称性取1/4作为研究模型。分析模型(见图1)中考虑基坑深20 m。临近地铁区间与基坑最近净距5 m，隧道埋深17 m。

由于基坑边沿到模型边界的距离是建模时必须考虑的重要因素。取基坑开挖深度的4倍～5倍，对四周竖向边界面的垂直方向水平位移进行约束，对底部边界面约束竖向位移和水平位移。开挖基坑尺寸为26 m(宽)×40 m(长)×20 m(深)，整体建模范围取130 m(宽)×140 m(长)×90 m(深)。

土体模拟考虑上海软土地区典型地层(见表1)，利用修正剑桥模型。连续墙结构和隧道衬砌结构的计算参数如表2所示[15-16]。

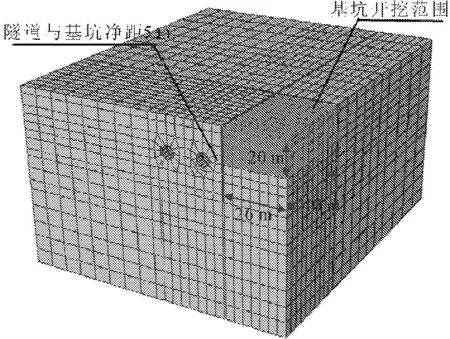
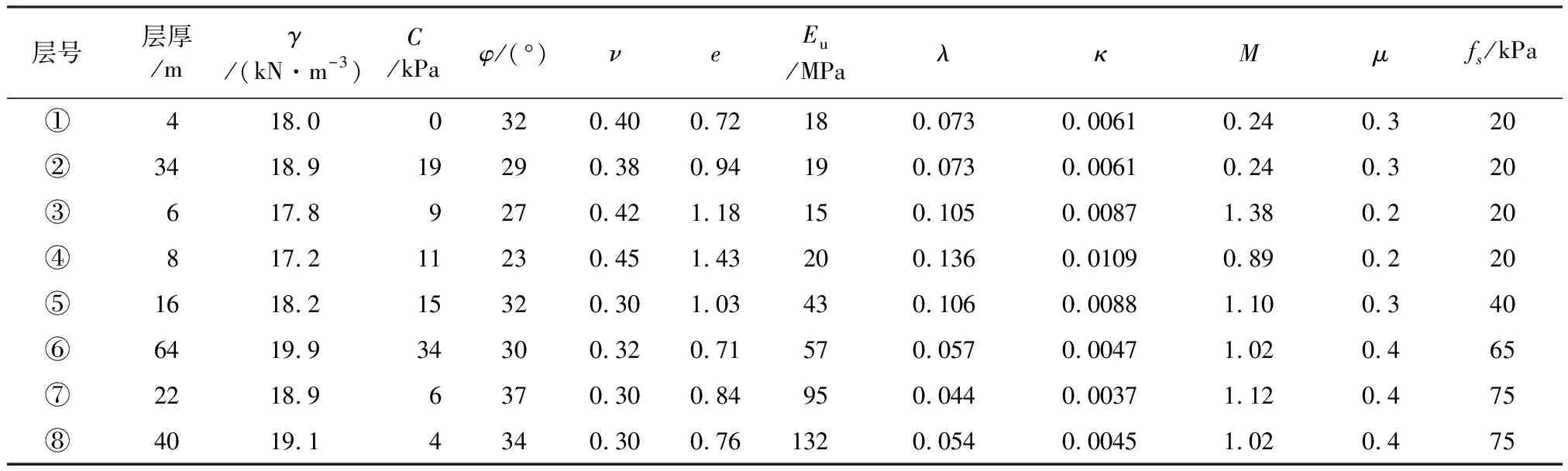
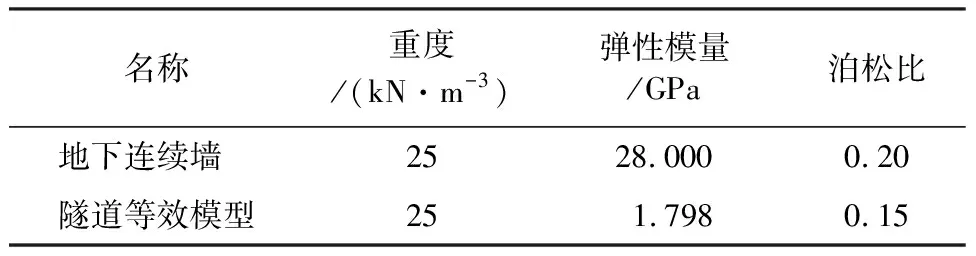
表2 结构计算参数

此外，连续墙和土体之间的接触采用面-面接触算法，考虑实际开挖分析步建立模拟实施的过程。

2 隧道衬砌纵向受力分析

在基坑开挖以前，既有隧道受上部土体和周围土体的作用，隧道衬砌在横断面上沿隧道纵向表现为受压状态，由于邻近基坑开挖的作用，原有的衬砌横断面受压状态将被打破，出现应力重新分布。

2.1 隧道纵向应力整体分析

本算例中，基坑沿隧道纵向开挖范围为40 m，由基坑开挖对隧道轴向应力沿纵向分布云图(见图2)可知，隧道横断面的正应力沿隧道纵向方向主要存在于距基坑开挖中心60 m范围内，即基坑沿隧道纵向开挖长度1.5倍。在影响显著的56 m范围内，根据隧道横断面应力重分布明显的区段，将隧道纵向分为A、B、C、D四个区域，其中，A、D为受拉趋势区，B、C为受压趋势区。

当基坑开挖后，隧道纵向在基坑开挖长度范围内出现向基坑一侧变形，这种变形导致了隧道衬砌在A、D两个区域的横断面正应力呈受拉趋势，而B、C两个区域的隧道横断面呈受压趋势。由于隧道衬砌在基坑开挖之前沿纵向有整体的受压应力，因此，在基坑开挖后，隧道衬砌A、D区域的受压应力将得到缓解，并可能表现为受拉状态，而B、C两个区域的受压应力则呈现加剧趋势。

结合实际隧道衬砌的状况，如果A、D区域出现受拉应力，该拉应力将由链接隧道衬砌的螺栓承担，若拉应力过大，链接螺栓将发生受拉屈服。如果B、C区域的压应力进一步加大，混凝土衬砌将承受被局部压碎的危险。

沿隧道纵向取三个典型断面(见图3、图4、图5)研究横断面正应力分布，图3中截面左侧呈现明显受压趋势；当隧道距离基坑开挖中心截面40 m处时(见图4)，隧道左侧表现出受拉趋势；之后，随着隧道继续远离基坑开挖中心截面，隧道衬砌断面应力逐渐趋于均匀，且整个横断面表现为受压状态，如图5所示。

图6为基坑开挖对邻近地铁隧道横断面弯矩影响图。由图6可看出，隧道沿纵向距离基坑开挖中心截面0～32 m范围内弯矩为正，即邻近基坑一侧隧道正应力有受拉趋势；在距离基坑开挖中心截面32 m～60 m范围内弯矩为负，即远离基坑一侧隧道正应力有受拉趋势；60 m以后弯矩基本为零，即隧道衬砌正应力恢复开挖前的应力状态。另外，隧道横截面弯矩沿纵向出现的两次峰值，分别位于距离基坑开挖中心截面20 m和44 m处，最大弯矩值分别为2 631 kN·m和-2 109 kN·m。

因此，根据隧道衬砌的受力状态及其最可能发生破坏的位置，将隧道沿纵向分为三个区域危险区Ⅰ、危险区Ⅱ和无影响区，具体位置如图2所示。

2.2 隧道纵向路径正应力分析

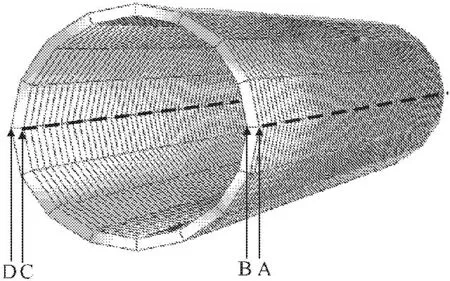
为了进一步研究隧道衬砌横截面所受正应力沿隧道纵向的分布状态，在隧道纵向方向上，沿隧道纵向建立如图7所示的四条分析路径(即横断面上某点沿隧道纵向上的连续节点)，路径A位于隧道最右端外侧、路径B位于隧道最右端内侧、路径C位于最左端内侧和路径D位于隧道最左端外侧，每条路径上选取间隔，分别考虑每条分析路径隧道衬砌的正应力状态，得到不同路径正应力沿隧道纵向分布图，见图8。

考虑四条路径下内外两侧横截面所受应力，整体而言，在距离基坑开挖中心前60 m范围内，隧道衬砌横截面应力变化较大，当距离基坑开挖中心超过60 m后，隧道衬砌横截面应力基本没有波动，表现为隧道衬砌开挖前的自身受力状态。

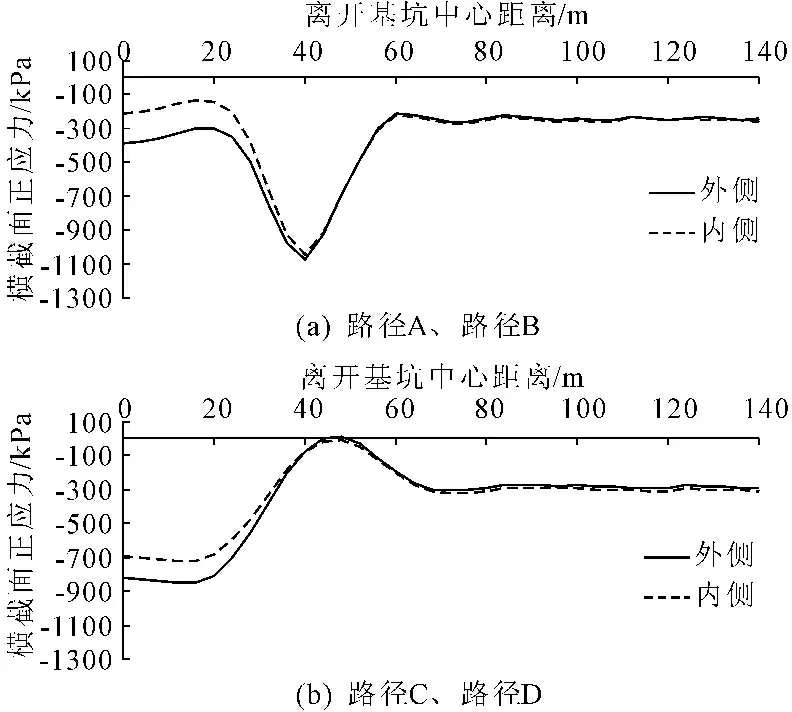
图8 不同路径横截面正应力沿隧道纵向分布曲线

(1) 图8(a)为路径A隧道衬砌内外两侧所受正应力沿隧道纵向的分布。该路径上，隧道衬砌开挖前承受300 kPa左右的受压应力。

在危险区Ⅰ范围内，隧道受拉趋势区(A区)内侧的压应力小于外侧承受的压应力，且内侧压应力在130 kPa左右，外侧压应力在320 kPa左右。可见，在该范围内衬砌内侧表现出明显的受拉趋势，而外侧反而受压趋势加强。这是由于在基坑开挖前，隧道在周围尤其是上部土体作用下，呈现横向鸭蛋变形的趋势，这种变形使得隧道最左侧和最右侧衬砌对周围土体的挤土作用非常明显。当基坑开挖以后，隧道危险区范围Ⅰ有向基坑一侧侧移的趋势，这种侧移加剧了隧道右侧对周围土体的挤土作用，作为反作用力，这种局部的土体对隧道右侧衬砌的作用使得隧道内外侧衬砌的应力出现了重新分布，最终使得隧道右侧衬砌的内表面表现出受拉趋势，而未表明的受拉趋势被削弱，甚至表现为受压趋势。

在危险区Ⅱ范围内，隧道衬砌内外表面所受应力基本相同，且受压趋势明显加强，最大受压应力位于距离基坑开挖中心断面40 m处，最大受压应力为1 079 kPa。

(2) 图8(b)为路径B隧道衬砌内外两侧所受正应力沿隧道纵向的分布。与路径A相同，该路径上，隧道衬砌开挖前同样承受300 kPa左右的受压应力。

在危险区Ⅰ范围内，隧道受压趋势区(B区)衬砌内侧压应力在700 kPa左右，外侧压应力在900 kPa左右。衬砌外侧承受的压应力趋势比内侧明显，这与隧道局部弯曲后衬砌截面的内力分布趋势相同。

在危险区Ⅱ范围内，隧道衬砌内外侧所受应力基本相同，且衬砌受拉趋势显著。此时，并未出现衬砌内侧拉应力趋势显著的现象，最大受拉趋势表现在隧道衬砌外侧，这是由于此处未出现隧道左侧的位移，未产生对隧道左侧土体的挤土作用，因此，受拉趋势在衬砌截面上按照正常分布。在距离基坑开挖中心截面48 m处出现拉应力，该拉应力发生在衬砌外侧，大小为12.68 kPa。

(3) 综合图8(a)和图8(b)可以看出，隧道衬砌在距离基坑开挖中心截面20 m和44 m处，最左端和最右端的应力差最大，该现象与隧道衬砌截面弯矩沿隧道纵向分布一致，此两处位置的弯矩出现两次峰值。

2.3 局部分析

为了进一步明确隧道横断面局部的应力分布，沿隧道纵向分别选取沿隧道纵向距基坑中心0 m、8 m、16 m、24 m、32 m、40 m、48 m、56 m、64 m、72 m和80 m处的横断面正应力进行分析。可以明确的看出不同隧道衬砌截面下的内力分布，以及其沿隧道纵向距离基坑开挖中心截面的位置不同而发生的变化。具体对以上不同截面的内力分布研究分析如下：

(1) 整体而言，沿隧道纵向衬砌的内力分布趋势合乎前节已定义的隧道三个区域。在危险区Ⅰ内，截面0°位置的受压应力小于180°位置；在危险区Ⅱ内，截面180°位置的受压应力小于0°位置，在图9(g)中180°位置出现了受拉应力；在无影响内，截面不同受压应力逐渐趋于平衡。

(2) 在危险区Ⅰ内的截面，0°和180°附近处(向上和向下各45°)的内侧受压应力均小于外侧受压应力，但其原因不同。0°处所出现的内侧受压应力小于外侧受压应力是由于隧道衬砌右侧土体对隧道的反作用力导致，而180°处所出现的内侧受压应力小于外侧受压应力则是由于整体受弯变形趋势引起。

(3) 在横断面上，0°和180°处的应力差在某种程度上反映了该截面上弯矩的大小。在此11个断面应力分布中，距离基坑中心截面40 m处断面的0°和180°应力差最大，此处弯矩也最大，该趋势与横断面弯矩沿隧道纵向分布趋势相一致。

(4) 从横断面距基坑中心40 m后，隧道衬砌内侧与外侧应力基本一致，这是由于沿隧道纵向在距基坑中心断面40 m后没有出现局部土体对隧道衬砌的挤压作用。

3 隧道纵向等效刚度对隧道结构纵向受力的影响

本节重点考虑隧道等效刚度在基坑开挖对隧道纵向影响中的作用，在基本模型中，隧道纵向等效刚度折减系数为0.069 5，另外，分别考虑隧道纵向等效刚度折减系数为0.380 0、0.690 0和1.000 0时的隧道模型，此三种情况同样考虑隧道横向等效刚度折减系数为0.750 0，因此，除基本模型外，分别建立隧道等效刚度为9.833 GPa、17.854 GPa和25.875 GPa的计算模型。

3.1 隧道横截面弯矩沿隧道纵向分析

图9为隧道不同等效刚度对隧道横截面弯矩的影响。从图9中可以看出，随着隧道刚度的增大，隧道横截面弯矩出现明显的增幅，尤其是隧道离开基坑中心截面20 m至40 m区间内，隧道衬砌承受了方向更为剧烈的弯矩突变，这表现在内力上，即隧道衬砌沿轴向的应力变化更为加剧。当等效刚度为1.798 GPa时，隧道横截面最大弯矩出现在距基坑中心截面20 m处，当等效刚度增加为9.833 GPa时，隧道横截面最大弯矩出现在距基坑中心截面44 m处。

针对四种不同隧道等效刚度，取距离基坑中心截面44 m处，当等效刚度逐步增大时，隧道横截面最大弯矩值分别为-2 109 kN·m、-8 562 kN·m、-11 589 kN·m和-14 246 kN·m，增量分别为6 453 kN·m、3 027 kN·m和2 657 kN·m，随着隧道等效刚度的增加，隧道横截面弯矩随呈收敛趋势，但增量非常巨大。这是由于，隧道刚度的增大，隧道抵抗周围土体对其作用力所导致的变形能力增强，其必然要承受更大的弯矩作用。可见，上小节分析隧道刚度增大后隧道纵向位移有较明显的减弱，这种纵向位移的减弱是以隧道衬砌承受更大的内力作为代价。

另外，由于本节所采用不同的等效隧道刚度是由连续体隧道刚度乘以不同的折减系数得到，可见隧道等效刚度折减系数的选取非常重要，其直接决定了数值模拟结果中隧道衬砌内力的分布。

3.2 隧道横截面正应力沿隧道纵向分析

通过对不同隧道等效刚度下隧道四条典型纵向路径的应力分布进行分析可以发现：

(1) 不同隧道等效刚度下，对于危险区域I内，隧道衬砌内侧受压应力均小于外侧受压应力。这是因为隧道变形对右侧土体局部的挤土作用，导致隧道右侧土体对隧道衬砌产生的反作用力导致，使得隧道内侧反而表现出更为强烈的受拉趋势。该结果再一次印证了此前的结论。

(2) 隧道衬砌内外侧的应力差仅存在于危险区域I内，沿隧道纵向距离基坑开挖中心截面距离大于30 m后，隧道衬砌的内外侧应力趋于一致。

(3) 整体来看，隧道衬砌的最大受拉趋势发生在距离基坑开挖中心截面20 m(此处位移隧道断面右端内侧)和44 m(此处位移隧道断面左端外侧)位置处，在这两个位置容易发生衬砌链接螺栓的受拉屈服。同样，隧道受压趋势也发生在这两个断面，不过距离基坑开挖中心截面20 m处的最大受压趋势发生在隧道断面左端外侧，距离基坑开挖中心截面44 m处的最大受压趋势发生在隧道断面右端外侧。

(4) 在隧道等效刚度较弱时，隧道衬砌断面应力的差异幅度较小，随着隧道等效刚度的加强，衬砌断面上应力差异的幅度增加明显，即相应断面的弯矩随着开挖深度加深而加大。值得注意的是，隧道受拉趋势区域出现了明显的大范围受拉应力，而且隧道等效刚度越大，受压趋势区域的受拉应力也越大，这种现象对于隧道的变形和稳定是十分不利的。这也说明，隧道纵向变形随着等效刚度的增强而减小，这一过程是以隧道衬砌或链接螺栓承受更大的应力作为前提的。因此，隧道等效折减系数的选取，在整个基坑开挖对邻近隧道纵向影响分析中有着重要的意义。

4 结 论

(1) 利用三维数值模型系统研究了软土地区基坑开挖对地铁隧道纵向影响规律，将隧道沿纵向分为危险区Ⅰ、危险区Ⅱ和无影响区。无影响区内，隧道由于既有应力的作用，衬砌断面处于受压状态；在危险区Ⅰ，邻近基坑一侧隧道衬砌断面有受拉趋势，另一侧呈受压趋势；在危险区Ⅱ，邻近基坑一侧隧道衬砌断面有受压趋势，另一侧呈受拉趋势。因此，危险区Ⅰ和危险区Ⅱ的衬砌截面弯矩相反。

(2) 通过对隧道衬砌的局部应力分析发现，在危险区Ⅰ范围内，隧道衬砌截面最左端和最右端附近的内侧受压应力均小于外侧受压应力；危险区Ⅰ以外的区域，隧道衬砌截面内侧和外侧应力一致。在危险区Ⅰ内隧道衬砌截面，0°和180°附近处(向上和向下各45°)的内侧受压应力小于外侧受压应力，但其原因不同。0°处所出现的内侧受压应力小于外侧受压应力是由于隧道衬砌右侧土体对隧道的反作用力导致，而180°处所出现的内侧受压应力小于外侧受压应力则是由于整体受弯变形趋势引起。

(3) 基坑开挖对临近地铁隧道的影响中，隧道等效刚度折减系数的选取尤为重要，其直接决定了数值模拟结果中隧道衬砌内力的分布。