让学生选择喜欢的方法来探究

王俊琴

教材分析：“植树问题”是人教版数学教材五年级上册第八单元的内容。本单元主要目的是向学生渗透有关植树问题的一些思想方法。教材将“植树问题”分为两端都栽、只栽一端、两端都不栽、环形情况以及方阵问题等几个层次，本节课主要是教学两端都栽的植树问题。教材以学生比较熟悉的植树活动为线索，让学生选择喜欢的方法来探究栽树的棵数和间隔数之间的关系，经历猜想、试验、推理等数学探索的过程，并启发学生透过现象发现其中的规律，建立数学模型，再利用规律解决生活实际问题。

学情分析：从学生的思维特点看，五年级学生仍以形象思维为主，但抽象思维能力也有了初步的发展，具备了一定的分析综合、抽象概括、归类梳理的数学活动经验。

教学目标：

1.通过分析、假设、操作等活动，使学生初步体会两端都栽的植树问题的规律，构建数学模型，解决生活中的有关问题。培养学生的数学应用意识和解决实际问题的能力。

2.培养学生的探究能力和研究意识，感悟一一对应、数形结合、变中不变、模型、化归、抽象、推理等数学思想方法。

3.使学生经历数学模型建立的过程，积累活动经验，提高数学素养。

教学重点：发现并理解两端都栽的植樹问题中间隔数与棵数之间的规律。

教学难点：建立植树问题的数学模型，运用“植树问题”的解题思想解决生活中的实际问题。

教学准备：课件、助学单、小树和小路模型

教学过程：

一、创设情境，引入新课

左右手反应能力训练。

师：经常活动手指可以使大脑更加灵活，而且一双手上隐含着许多的数学问题，每两个手指之间的空在数学中叫“间隔”，数一数你的手上有几个间隔？间隔数是4，对吧？今天我们就一起研究和间隔有关的问题。（板书课题）

设计意图：本环节以学生最熟悉的手引入，来理解“间隔”“间隔数”的含义，以此作为本节课学习语言的铺垫，让学生初步体会两端都植树，棵数比间隔数多1的问题。

【评析】利用一个人人自带的免费“学具”：伸出一只手，展示“五指四空”，简约形象而又不失典型性的数学模型，这样的引课学生喜欢，久用不衰。

二、充分经历、探究新知

1.出示校园图及大队部招聘广告。

（1）读一读，说一说

师：你是如何理解这句话的？（借助小树和小路的教具模型理解“一边”“两端都栽”的含义）

生：在马路的一边栽，两端都栽。（学生上黑板拿老师准备好的马路和小树演示“在一边栽”和“两端都栽”的意思）

师：如果你是小设计员，你会考虑什么问题？

生1：总长是多少？

生2：每隔多长栽一棵？

生3：一共要栽多少棵树？

引导学生变被动为主动，提出数学信息和数学问题，同时理解“总长”“间隔长”“间隔数”“棵数”等概念。

设计意图：布鲁纳认为：“学习是主动的过程，对学生学习兴趣的最好激发是让其对所学材料感兴趣，即主要来自学习活动本身的内在动机，就是直接推动学生主动学习的心理动机。”

我国著名数学家华罗庚也指出：“人们对数学早就产生了枯燥乏味、神秘、难懂的印象，原因之一就是脱离了生活实际。”

本课从学生最熟悉的校园生活引入，以大队部招聘信息为素材激发学生学习兴趣和探究欲望。引导学生站在设计师的角度上理解情境，提出数学信息及数学问题。开放的情境创设既激发了学生兴趣、调动了学习的积极性，同时也培养了学生发现问题、提出问题的能力，培养了学生的创新意识。

【评析】借助现实情境让学生充分感知“两端都栽”的含义，同时理解间隔长和间隔数与总长之间的关系，体会数学来源于生活的理性精神。

2.借助操作，探究规律。

（1）假设

师：以小组为单位，自己假设一个总长和一个间隔长，并求出棵数。

（2）小组操作探究

①通过画一画的方法找到自己小组假设情况下的“间隔数”和“棵数”分别是多少。

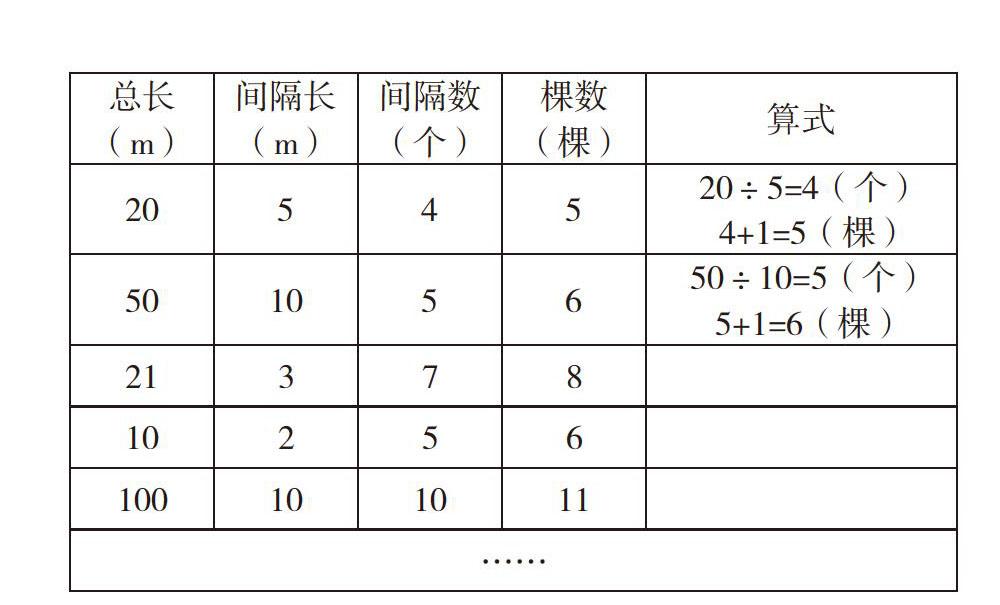
②汇报填表（五组学生上台填写汇报）

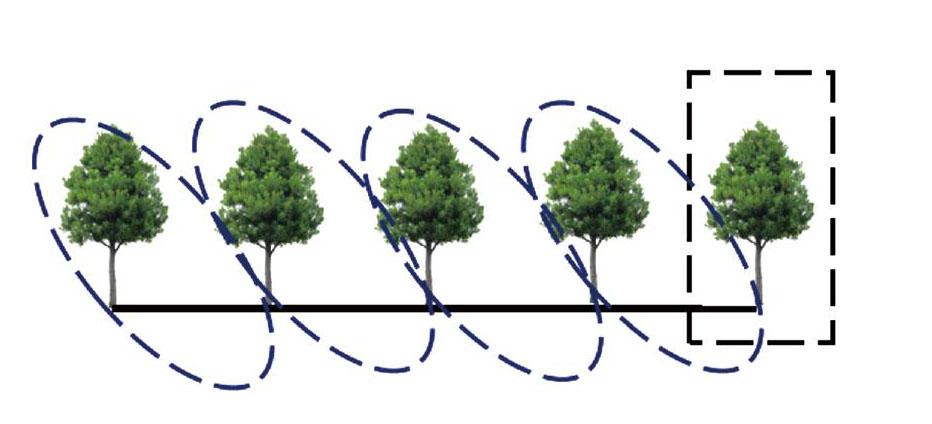
第一组学生：我们组假设总长为20米，每隔5米栽一棵，这是我们组画的图，一共有4个间隔，5棵树。

第二组：……

预设：a.学生选择的“总长”可能会较大，“间隔长”较小，在操作的过程中亲身感受研究的繁琐，主动调整数据，体会化繁为简思想。

b.学生选取的“总长”和“间隔长”不是倍数关系，这种情况下不能保证两端都栽树，培养学生的数感。

设计意图：数学家弗赖登塔尔认为，数学学习唯一有效的方式是“再创造”。本环节充分放手，运用几何直观性，让学生用画图的方法模拟植树，描述和分析问题，借助几何直观性把较复杂的问题变得简明、形象，让学生经历了知识形成的过程，感知植树问题在两端都栽的情况下，间隔数和棵树之间的关系。同时，使学生在“做”的过程和“思考”的过程中积累数学活动经验，提高数学素养。

【评析】学生自主选择一个总长和一个间隔长并求出棵数，尊重学生的主体地位。同时通过小组操作探究，让学生体会复杂问题简单化的数学思想，也为后面发现规律做了很好的铺垫。

（3）观察发现规律

师：总长、间隔数、间隔长、棵数都在变化，但有一个规律是不变的，你发现了吗？（体会变与不变思想）

生：棵树总比间隔数多1。

师：棵数为什么总比间隔数多1呢？

借助所画图理解一一对应思想。（讨论、汇报）

生1：因为根据我们组画的图发现，第一棵树后面有5米，又一棵树又有5米，又一棵树后面又有5米……最后还有一棵树。

生2：因为一个间隔对应了一棵树，最后还有一棵树。

借助课件动画演示理解一一对应思想。（演示见下图）

设计意图：古希腊哲学家苏格拉底认为，虽然特殊的事件或事物在某些方面变化或消逝，但它们在某些方面是同一的，从不变化、从不消逝。小学数学学习的规律、性质等都是运用不完全归纳法得出的，即从大量变化的数据中发现不变的数学本质。因此，在教学中应创造机会让学生在变化的数据中找到不变的规律，体会变与不变的辩证关系，渗透变中不变的数学思想。

（4）抽象算式

师：在刚才的探究中，间隔数和棵数是数出来的，你能通过计算得出来吗？（填写算式）

小组内写出自己的算式。

第一组：20÷5=4（个）     4+1=5（棵）

①为什么用除法？（生：20除以5表示20米里面有几个这样的间隔）

②第一个算式中的商和第二个算式中的第一个加数分别表示什么意思？

生1：商的4表示4个间隔，加数4也表示4个间隔

生2：商的4表示4个间隔，加数4表示4个间隔对应的4棵树。

③为什么加1？

生：因为一个间隔对应一棵树，最后还多的一棵树，所以要再加1。

第二组：50÷10=5（个）     5+1=6（棵）

第三组：……

（5）抽象公式

师：在今天研究的两端都栽的植树问题中，你认为怎样求所植棵数？

生：总长÷间隔长=间隔数      棵数=间隔数+1

教师板书：总长÷间隔长=间隔数     棵数=间隔数+1

（6）前后呼应、回归例题：同学们在全长100米的小路的一边植树，每隔5米栽一棵（两端要栽）。一共要栽多少棵树？

生：100÷5=20（个）

20+1=21（棵）

答：一共要栽21棵树。

设计意图：抽象性是数学的基本特征之一。引导学生将几何直观的过程抽象成算式，培养学生的抽象思维。

3.抽象模型。

①师：生活中像这样的问题还有哪些？

生：路灯、挂灯笼、楼房、排队等等。

②师：这些物体，我们可以去掉他们华丽的外衣，以灯笼为例，无限缩小，最后变成数学中的点，这个点可以表示什么？（同时课件演示灯笼缩小变点）

③揭示本质：植树问题就是点和线之间的关系问题。

点数=线段数+1

设计意图：《义务教育数学课程标准（2011版）》指出：“教师要揭示知识的实质及其体现的数学思想。”“模型思想的建立是学生体会和理解数学与外部世界联系的基本途径。”植树问题的本质其实是数学中点与线关系的问题。本环节揭露数学本质，形成数学建模，渗透模型思想。

【评析】在发现规律、理解算式的意义，以及抽象出数学模型的过程中，让学生经历“每隔5米、10米、3米……栽一棵树”“每5米、10米、3米……一个间隔”“一个间隔对应一棵树”，三次层层递进的认识，也充分体现一一对应的数学思想，整个过程都是算式与图形结合，也体现了数形结合的数学思想。通过合作交流，发现几组算式中的变与不变，自然而然地找到棵数与间隔数之间的关系，透过现象看到本质：植树问题就是点和线之间的关系问题，点数=线段数+1。建立数学模型，培养学生言必有据的科学态度和严谨的思维习惯。

三、回归生活，实际应用

在一条全长2千米的街道两旁安装路灯（两端也要安装），每隔50米安一盏。一共要安装多少盏路灯？

四、课堂小结、提炼经验

1.今天你学到了什么？

2.活动过程梳理：分析→假设→操作→结论

3.拓展植树问题的另外两种情况，进行知识迁移。

设计意图：《义务教育数学课程标准（2011版）》指出：“推理能力的发展应贯穿于整个数学学习的过程中。推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。”通过本节课的学习与探究，引导学生能凭借经验和直觉，通过归纳和类比等方式推断出植树问题在其他情况中的间隔数与棵树之间的关系，培养学生的推理能力。

④詩词鉴赏：兴庆湖畔景色娇，一行垂柳一行桃。绕湖周长两千米，间隔五米全栽到。漫步湖边赏春色，可知桃柳各多少？

设计意图：《义务教育数学课程标准（2011版）》指出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系。”课后诗词鉴赏能使学科体会到生活中处处有数学，数学与其他学科的紧密联系。让学生带着问题来到课堂，带着问题离开课堂。

【评析】通过提供生活中的不同情境，让学生体会生活中的一些问题是与植树问题相同的，有利于让学生养成用数学的眼光观察现实世界的习惯，也有利于学生发展用数学的思维分析实际问题的能力。

机动练习：园林工人沿着一条笔直的公路一侧植树，每隔6米种一棵，一共种了36棵（两端都种），从第一棵到最后一棵的距离有多远？

【总评】

本节课的教学主要有以下几个特点：

1.从植树问题到建构植树模型需要一个“以小见大”的渐进过程。植树问题模型的建构不是一蹴而就的，需要让学生经历渐进过程。这节课通过三个层次帮助学生建构模型。

层次一：初步建构点段之间的一一对应关系。

师：以小组为单位，自己假设一个总长和一个间隔长并求出棵数。学生通过小组操作探究，用图示画出不同“总长”与不同“间隔长”，并算出对应的不同间隔与棵数。这样学生在操作的过程中初步建构点段之间一一对应的关系，而且能主动调整数据，体会化繁为简的思想。

层次二：发现模型关系。

学生从自己选择的10米、15米、25米、50米……的小路两端都栽树，每隔5米栽一棵，一共能栽多少棵树？借助画图进行验证，学生发现：无论是10米、15米、25米、50米，长度虽然不同，两端都栽，总长÷间隔长=间隔数，棵数=间隔数+1，多样的数据和丰富的认识有助于帮助学生深化点段之间一一对应的关系。

层次三：抽象出模型关系。

当学生有了丰富的认识后，教师提出了问题：生活中像这样的问题还有哪些？生：路灯、挂灯笼、楼房、排队等等。师：这些物体，我们可以去掉他们华丽的外衣，以灯笼为例，无限缩小，最后变成数学中的点，这个点可以表示什么？（同时课件演示灯笼缩小变点）揭示本质：植树问题就是点和线之间的关系问题，点数=线段数+1。

上述三个层次的设计，就是让学生经历“以小见大”的渐进过程。使学生在研究问题中由浅入深慢慢建构植树模型。

2.开放的学习方式让学生学得轻松愉快。

曾经听过其他教师执教这节课，总感觉教师带着学生一步一步地研究，学生确实不出差错，但是看得出学生学得很累。而这节课的教学，老师为学生提供有目标的小组合作与自主研究的空间，让学生交流发现了计算方法，且让学生自主经历建构植树模型的过程，学生学得轻松愉快。

3.巩固练习凸显植树模型的结构化。

这节课老师将植树问题拓展到相应的一类生活情境，如路灯问题、挂灯笼问题、排队问题，侧重点是巩固不同情况下点与段数之间的对应关系，使学生发自内心地感受到“看起来情境不同，但是它们都是一类题”，凸显模型的结构化，既达到举一反三的教学效果，又有利于培养学生透过现象揭示本质的洞察能力。