具有随机分形自适应搜索策略的蚁狮优化算法*

赵克新，黄长强，王 渊

（空军工程大学航空航天工程学院，西安 710038）

0 引言

蚁狮优化算法［1］（Ant Lion Optimizer，ALO）作为一种新的群智能优化算法，是澳大利亚学者Seyedali在2015年提出来的。相比于遗传算法［2］、粒子群算法［3］、人工蜂群算法［4-5］（Artificial Beecolony Algorithm，ABC）、蚁群算法［6］，由于蚁狮优化算法包含蚂蚁游走和蚁狮捕猎两种行为，在求解复杂函数优化问题时表现出了更强的探索能力和开发能力［7］。同时该算法具有调节参数少，易于实现等优点，引起了很多学者的关注。在建立离散滤波器模型［8］、解决无线传感网络的数据收集［9］问题、可再生分布式产能的优化配置［10］、解决无人机航迹规划［11-12］问题等方面表现出优越的性能。

ALO算法作为新的群智能优化算法，本身还有很多待优化的方面，蚂蚁在精英蚁狮的周围随机游走，步长随着算法迭代次数的增加而减小，算法在后期容易出现陷入局部最优［13］、收敛速度慢、搜索精度不高等问题，从而给算法的实际应用带来了负面影响［14-15］。针对这一问题，本文提出了一种具有随机分形自适应搜索策略的蚁狮优化算法（Ant Lion optimizer With Stochastic Fractal and Self-adaption Searching Strategy，SFSALO）。仿真结果表明，SFSALO算法很好地平衡了全局开发与局部探索能力，能够有效解决复杂多维函数的优化问题。

1 标准ALO算法

蚁狮优化算法的灵感来源于蚁狮幼虫捕食蚂蚁的行为：蚂蚁为了寻找食物在空间内随机游走，蚁狮在沙丘内利用设计好的锥形陷阱猎捕蚂蚁，当随机游走的蚂蚁落入陷阱，蚁狮便捕捉到了蚂蚁并重新挖好陷阱等待另外的蚂蚁。算法首先按照下式进行初始化：

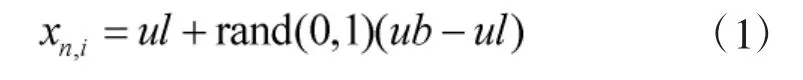
蚂蚁和蚁狮分别随机生成SN个初始解，并计算每个蚁狮位置的优劣或者适应度值，同时进行排序，全局最优值。式（1）中，xn，i表示蚂蚁或者蚁狮的位置，，ul和ub分别表示游走空间的下界和上界。蚂蚁随机游走数学表达式为：

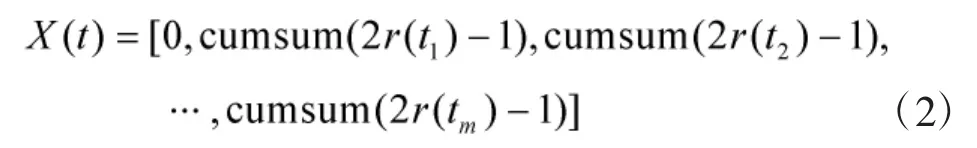
式（2）中，cumsum表示计算数组累；m为蚂蚁的数量；t为当前的迭代次数；r（t）是一个随机函数，如下：

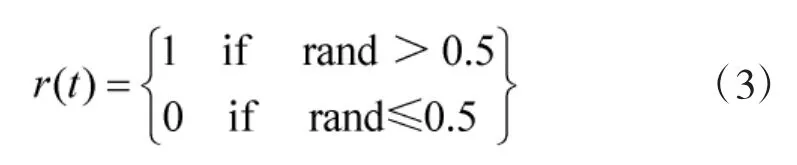
式（3）中，rand表示0到1之间的随机数。

下列矩阵保存蚂蚁的位置：

式中，d表示变量的维度，Ai，j表示第i只蚂蚁在第j维上的位置。通过适应度函数评价蚂蚁位置的优劣，蚂蚁的适应度值保存在如下函数矩阵：

蚁狮的数量与蚂蚁一致，其位置与适应度函数用下列矩阵表示：

式（4）中，d表示变量的维度，通过适应度函数MAP评价蚁狮的位置。蚂蚁在第i维的位置更新公式：

式（8）中，ai和bi为第i只蚂蚁随机游走的最小步长和最大步长；cti和dti分别为蚂蚁第t次迭代时的变量的最小值和最大值。cti和dti分别定义如下：

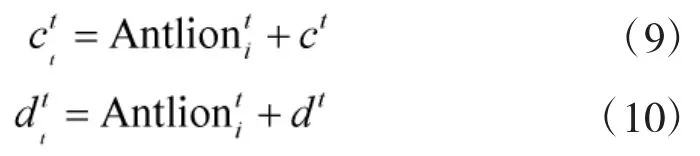
式中，ct表示蚁狮第t次迭代时变量的最小值和最大值。ct、dt的数学表达式如下：

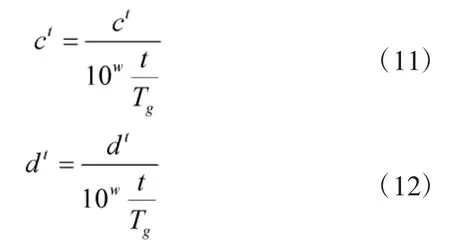
式中，w为常值，t表示当前迭代次数，Tg表示最大迭代次数。

ALO算法将每次迭代的精英蚁狮个体EAntlion保存下来，蚂蚁通过轮盘赌［20］的方式对蚁狮进行贪婪选择并和蚂蚁一样在自身周围随机游走，表达式如下：

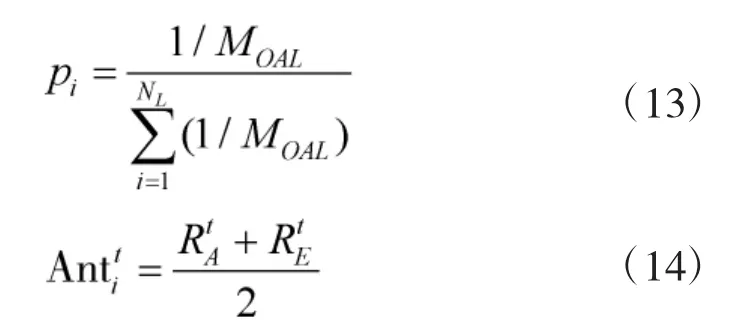
蚁狮在捉到蚂蚁后的位置更新公式如下：

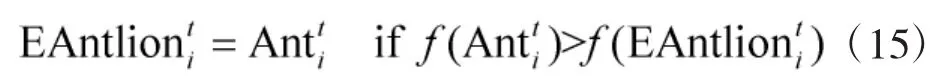
2 具有分形自适应搜索策略的蚁狮优化算法

群智能优化算法的探索与开发能力是决定算法效率的关键。开发能力指的是算法在特定区域内寻找并提取较优的解，探索能力是指在搜索空间内确定较优解的能力。ALO算法的蚂蚁和蚁狮位置更新方程因选择精英蚁狮进行游走而具有较强的开发能力。但同时可以看出，ALO算法的探索能力较弱，因而存在易陷入局部最优的问题。针对这一问题，提出了随机分形自适应搜索策略，该策略主要是根据蚂蚁的游走行为，提出了增强探索能力的随机分形搜索方程；根据蚁狮重挖陷阱的行为，提出了增强开发能力的自适应搜索方程。下面对提出的策略进行详细说明。

2.1 蚂蚁随机分形搜索方程

分形现象是自然界很常见的一种现象，例如植物的生长、山河的形成以及大脑皮层等，这种部分以某种方式与整体相似的形式称为分形。随机分形一般由不同的随机原则反复迭代产生。常用的随机原则有高斯游走（Gaussian Walk）、列维飞行（levy Flight）、自回避游走（Self-avoiding Walks）。列维飞行具有较强的全局搜索能力，将列维飞行与蚁狮优化算法中蚂蚁的搜索行为相结合，提出了蚂蚁随机分形搜索方程：

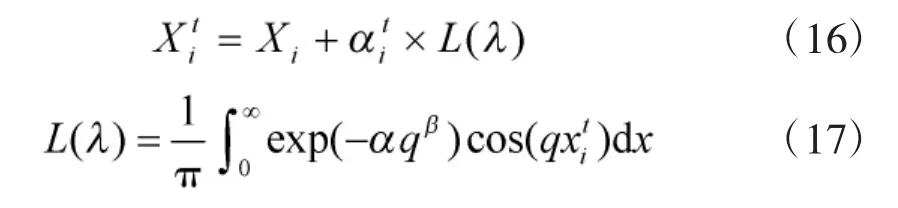
式中，q表示种群数量，α表示比例因子，Xi表示最初的蚂蚁位置。通过上述改进有效地提高了蚂蚁对整个解空间的探索能力。

图1 单个粒子随机分形示意图

2.2 蚁狮自适应搜索方程

标准ALO算法中蚁狮根据蚂蚁进行陷阱位置的调整，蚁狮与蚂蚁采用相同的搜索方程，经过对算法的原理分析得到：蚁狮的行为方式影响了算法对解的精细化搜索。所以受到文献［15］的启发，提出了蚁狮自适应搜索方程：

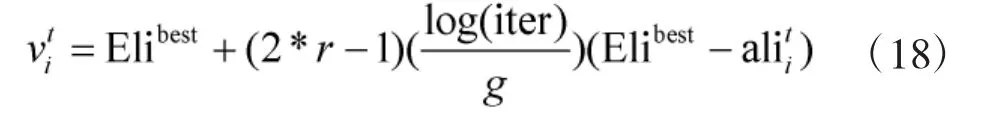
式中，r是0到1之间的随机数，Elibest表示蚁狮全局最优位置，表示种群i中第t只蚁狮的位置，iter表示当前迭代的次数。随着迭代次数的增加，蚁狮搜索范围自适应减小，在全局最优位置附近进行精细开发。

2.3 改进算法的分析与步骤

在标准的ALO算法的基础上引入随机分形自适应搜索策略，首先针对蚂蚁的行为引入随机分形原则，对其游走方程进行了改进，该方程利用列维飞行能够很好地对搜索空间进行探索。其次在蚁狮设置陷阱行为的基础上引入自适应因子，随着循环次数的增加，自适应地平衡算法的开发与探索能力。算法的具体步骤如下：

1）初始化算法的各个参数；

2）计算每个蚁狮对应位置的适应度值并记录全局最优值；

3）while结束条件不满足；

4）蚂蚁根据式（16）进行随机分形游走，并计算更新后的适应度值，与全局最优值进行比较，采用贪婪选择机制进行更替；

5）位置最佳蚁狮根据式（18）进行自适应陷阱设置，应用贪婪机制更新蚁狮最优位置；

6）判断当前迭代次数是否超过极限值，如果条件不满足，转至第4）步；否则进入第7）步；

7）结束循环，输出最优解。

3 仿真实验

3.1 实验环境与参数设置

为了验证本文提出的SFSALO算法的特性，选取了3个单峰，3个多峰基准函数作为被测函数，并与ABC算法、ALO算法的测试结果进行比较。实验硬件条件为 Inter（R）Core（TM）i5-6500，CPU，3.20 GHz，4 GB，RAM，Win7操作系统，仿真软件为MATLAB R2013a。3种算法种群规模SN设置为50和100，迭代次数macycle为300次，试验次数100次。通过对比100次独立实验的最优值、平均值、最差值、方差等参数，评价各个算法的优化能力。

3.2 结果分析

下页表1为6个基准函数的数学公式、理论最优值、搜索空间。为单峰测试函数，为多峰测试函数。图2是在50维下6个标准测试函数的收敛过程，表2为测试结果（100维收敛过程省略）。

表1 测试函数

从图2可以看出，改进后的SFSALO算法比标准的ALO算法具有明显的优势。分析图2（a）、2（b）、2（c）可知，在对单峰测试函数进行寻优时，SFSALO算法的收敛速度明显快于ALO算法，并总能够找到理论最优值，而标准ALO算法却很难达到理论最优值；分析图 2（d）、2（e）、2（f）可知，在对多峰测试函数进行寻优时，SFSALO算法在对测试函数4和5寻优时，可以在较少的迭代次数内收敛到理论最优值，寻优的寻优精度强于标准ALO算法。在对函数6进行寻优，虽然SFSALO算法没有收敛到理论最优值，但是收敛精度和速度明显优于ALO算法。

通过下页表2可以看出，改进后的算法无论是收敛精度还是稳定性，都优于标准的ALO算法，SFSALO算法对于单峰还是多峰函数都具有较好的适应性。在对复杂函数进行寻优时，蚂蚁的随机搜索具有很好的探索性，不容易陷入局部最优值；蚁狮的自适应搜索具有很好的开发性，能够在适应度较高的位置附近进行精细搜索。改进后的算法很好地平衡了开发能力与探索能力。

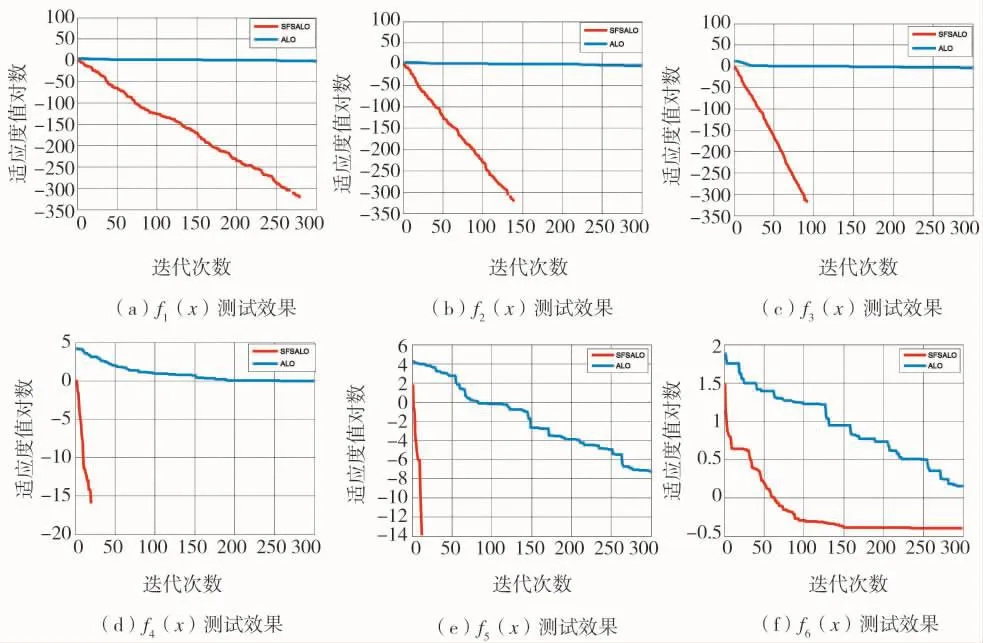
图2 不同基准函数的测试收敛过程

为了进一步说明SFSALO算法的优越性，对ABC算法，PSO算法，GWO算法进行了比较，维度设为50，最大迭代次数为300。图3和图4分别是4种算法对Sphere函数、Griewank函数的收敛过程对比。

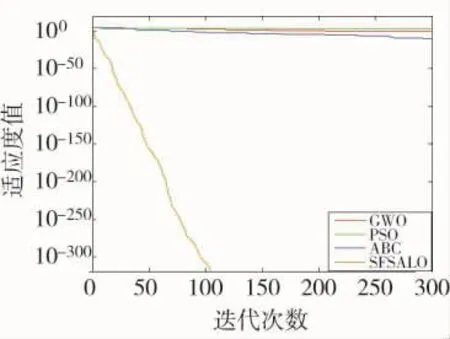
图3 Sphere函数收敛曲线

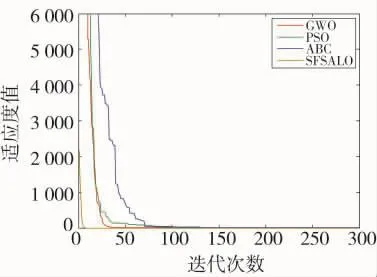
图4 Griewank函数收敛曲线

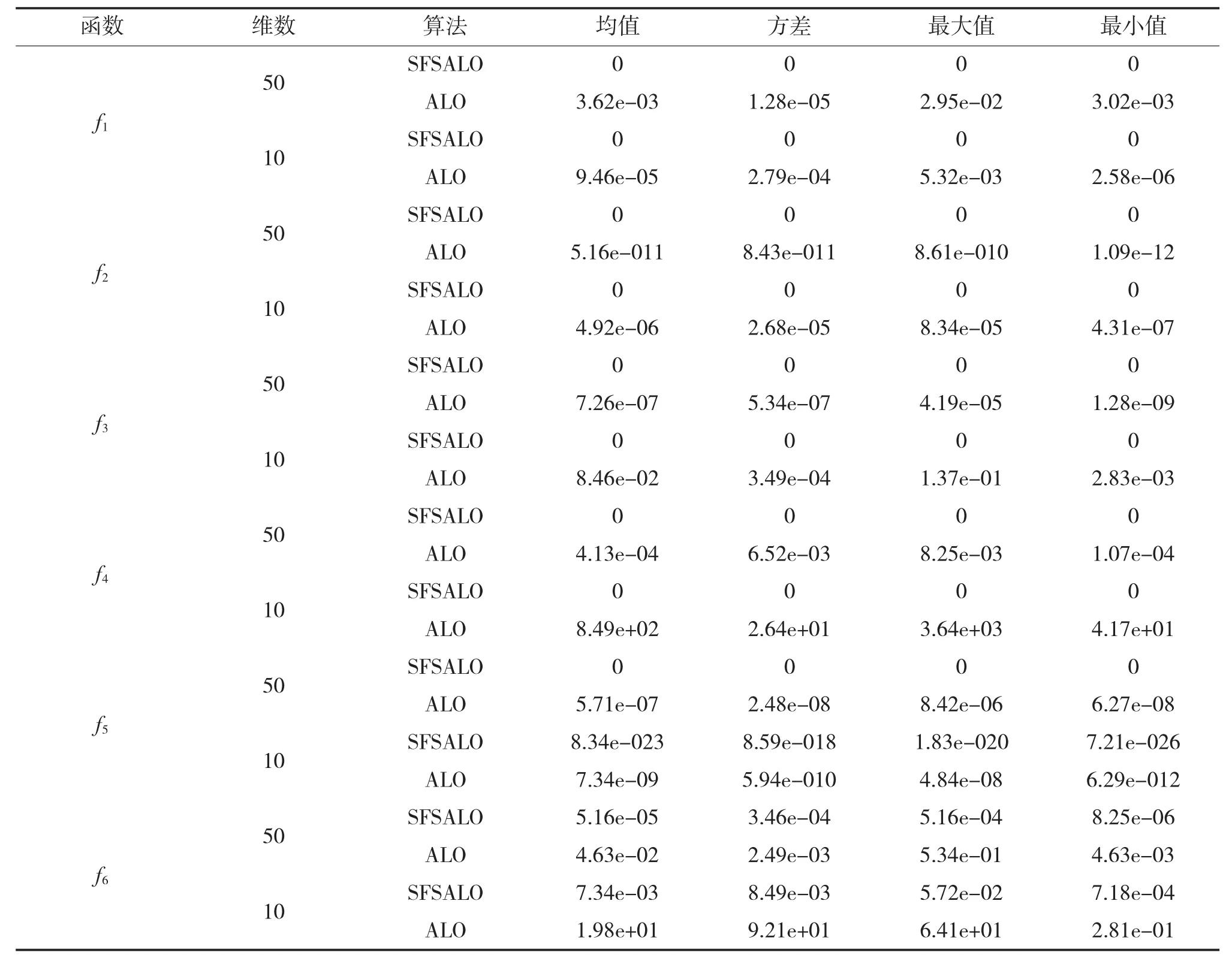
表2 6个标准测试函数仿真结果比较（50维）

仿真结果分析表明SFSALO算法的收敛精度和收敛速度明显比其他3种算法效果显著。对Sphere高维单峰函数和Griewank多峰函数进行优化时，SFSALO算法在较少的迭代次数内都可以搜索到理论最优值。

4 结论

为了解决标准ALO算法易陷入局部最优值和收敛速度慢等缺点，更好地平衡算法的开发与探索能力，在随机搜索思想的启发下，结合自适应策略，提出了具有随机搜索自适应蚁狮优化算法。改进后算法中的蚂蚁通过随机搜索方程提高了探索能力；蚁狮利用自适应搜索的方式对自身进一步精细开发，两者协作共同提高了算法的全局搜索能力。通过对单峰、多峰函数进行测试，并且与其他常见的几种算法进行比较，充分表明了SFSALO算法具有收敛速度快、寻优精度高、适用广泛等优越的性能。