机械臂设计方案选择的模糊综合评价方法*
2019-03-14张继明李宪华
张继明 ,张 军 ,李宪华 ,疏 杨 ,袁 翔
(1.安徽理工大学机械工程学院,安徽 淮南 232001;2.公牛集团,浙江 宁波 315000)
0 引言
随着机械臂越来越多地应用在生产工作中,必须设计出更符合实际情况的机械臂,这就需要从众多方案中选出更适合的设计。而目前先进设计技术的理论方法种类繁多,不同的研究人员对所选对象性能要求不同,则所选设计方案不同。特别是在设计的初始阶段,往往根据设计的目标会形成多种设计方案,在实际过程中如何确定最佳设计方案成为后续工作的关键[1]。
如何使设计出的机械臂,既满足预期功能,又性能好、效率高、成本低,在预期使用期限内安全可靠,操作方便,维修简单和造型美观是每一个设计者设计前必须要考虑的问题。机械臂设计方案的研究是涉及到多个层次、多个目标的综合评价对象,需要来自各种学科背景的专家和决策者,共同参与对机械臂的设计方案进行评价,以保证评价结果的可信度和准确性。沈健[2]借助于层次分析方法,对直角坐标机器人设计方案进行多层次模糊综合评价;唐骏[3]通过熵权法和模糊综合评价法对登陆地点进行选择等。在机械臂设计的初始阶段,方案的多样性和复杂性给方案的选择评价带来了很多的困难。因而,建立机械臂设计方案的评价指标体系,对于方案的评价分析有着重要的意义。
文中提出了基于熵权和层次分析法对机械臂设计方案选择的评价体系,并综合模糊理论,对机械臂设计方案选择进行综合评价。
1 模糊熵权综合评价方法
1.1 模糊综合评价法
模糊综合评价方法具体的步骤为:
3)建立模糊评判矩阵:单因素评判矩阵是指以各单因素评判集的隶属度为行组成的矩阵:
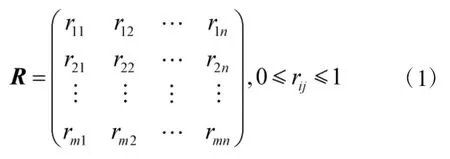
其中,rij为P中因素pi对于V中等级vj的隶属度关系。

从而可以得出目标层的模糊隶属度。
1.2 综合权重的确定
为了在主观赋权的基础上得到更能反映客观要求的权重,本文结合熵权评价法[9-15]和层次分析法[6-8]进行综合权重的确定。
1.2.1 熵权法确定指标权重
如果某评价指标的熵权越小,该指标提供的信息量就越大,在综合评价中所起的作用就越大,权重就越高。熵权表示的意义是在各种评价指标值确定的情况下,各指标在竞争意义上的相对激烈程度系数[4]。其计算方法如下:
1)数据标准化
对于专家给出的权重向量进行合并,得出判断矩阵R:
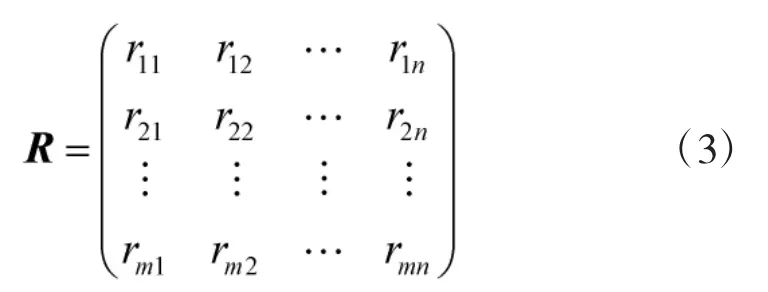
2)将判断矩阵R进行归一化,得到归一化矩阵Q,Q的元素为

3)求各指标的信息熵

4)确定各指标权重(熵权)
根据熵权法定义,则系统数据的熵权wj为:
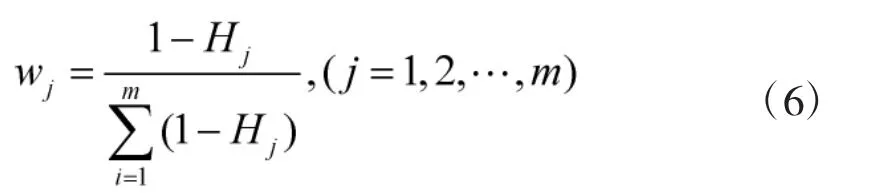
1.2.2 用AHP法确定指标权重
建立层次结构后,通过上下层元素两两比较构造判断矩阵,在构造判断矩阵中,要对判断矩阵进行一致性检验并计算各元素的权重向量。
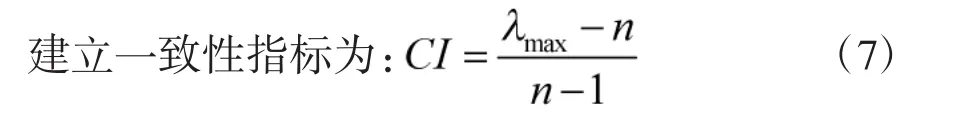
式中,n为判断矩阵的阶数。

若CR越小,表示判断矩阵的一致性越好。当CR<0.10时,认为判断矩阵的一致性是可以接受的,否则应对判断矩阵作适当的修改,直到其一致性可接受为止。
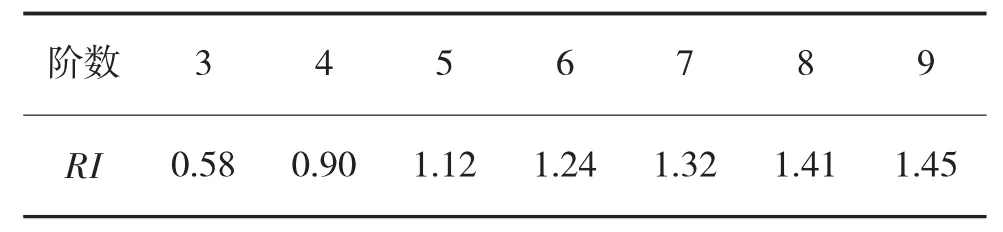
表1 平均随机一致性指标
1.2.3 确定评价指标的综合权重
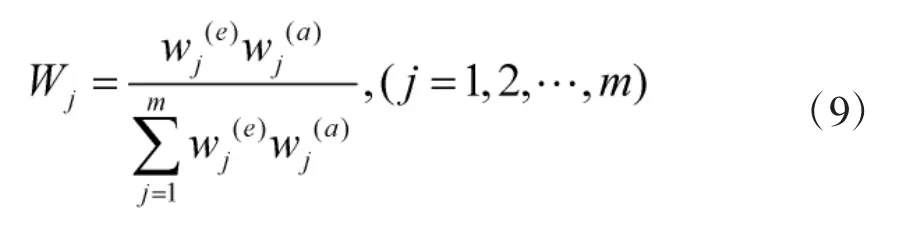
2 基于模糊熵权的机械臂设计选择
2.1 综合评价体系模型建立
通过综合以往的研究结果,结合机械臂设计阶段的特点,提出了以主要性能、经济性、适应性和其他等4个方面作为评价指标体系的准则层,机械臂设计选择的具体评价体系如图1所示。
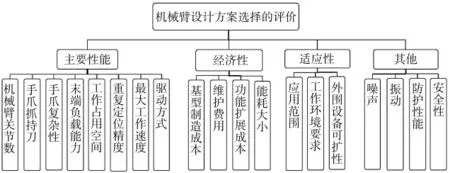
图1 机械臂设计方案选择的综合性能评价层次模型图
为了进一步说明上述模型方法的应用,表2列出了机械臂设计方案各评价指标的评语集合数据,下面均以此表进行计算求解。
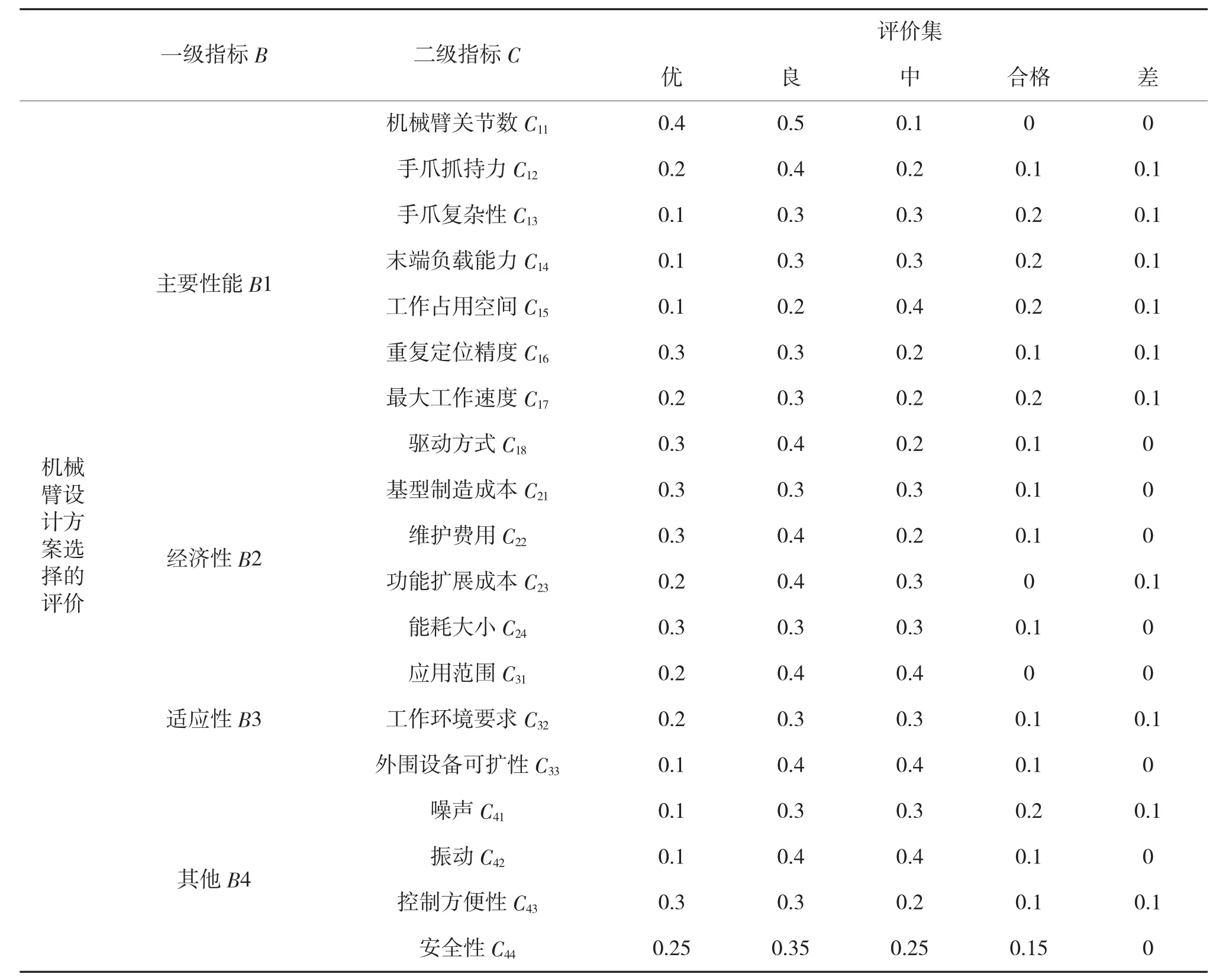
表2 机械臂设计方案评价指标的权重及评语集合数据
2.2 熵权法指标权重的计算
通过专家打分,得出指标主要性能指标下的二级指标的模糊评价矩阵:
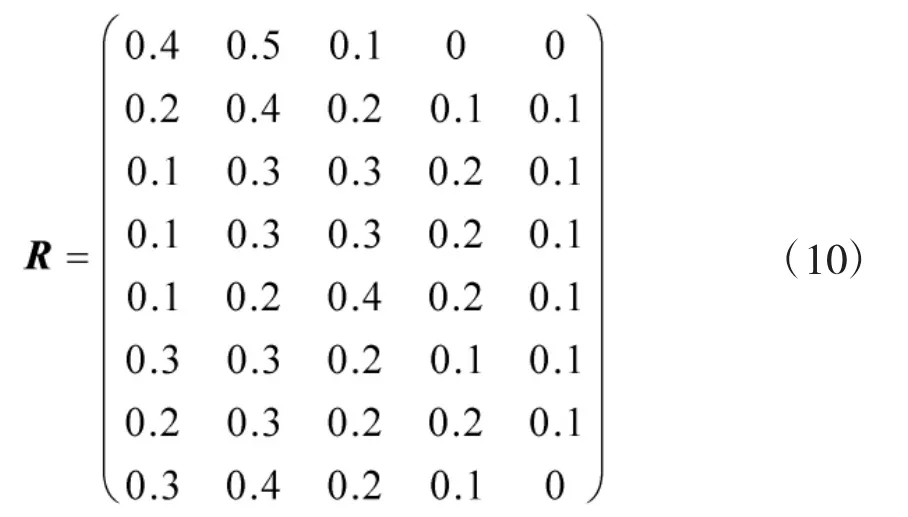
然后求得其熵和熵权,如表3所示。
同理可得经济性指标、适应性指标和其他指标的熵和熵权,如表4所示。
2.3 层次分析法指标权重的计算
根据图1的层次结构,经过专家的讨论,并结合相关指标的度量值,得到主要性能指标、经济性指标、适应性指标及其他指标下的权重及其所包含的二级指标的权重分布。
由表5可知,指标层对准则层的指标权重结果大小情况,且每个矩阵的CR值均小于0.10,则一致性检验均通过。

表3 主要性能指标的熵及熵权

表4 经济性指标、适应性指标和其他指标的熵及熵权
由上述熵权法指标权重的计算结果和层次分析法指标权重的计算结果对比分析得出,假如只选用前者确定权重,则在主要性能指标中机械臂关节数权重最大,其次是驱动方式,若对于层次分析法确定的权重,此性能指标中权重最大的为手爪抓持力,其次为重复定位精度指标,对于其他指标情况类似。这样的话两种方法有两种选择结果,原因就是每一种方法的使用都存在主观性,并不能完全反应指标对方案的影响程度,因此,有必要把两者的结果进行合成,得到更能真实的反应指标的实际情况。
2.4 确定评价指标的综合权重
根据模型中综合权重的式(9),可求出主要性能指标集合中各指标的综合权重为:W1=(0.140 7,0.187 8,0.034 7,0.081 0,0.125 0,0.117 9,0.049 7,0.263 1),则最终的评价结果为 B1=(0.242 2,0.360 7,0.222 5,0.115 0,0.059 6),结果表明,有 24.22%的人认为这种机械臂设计时主要性能指标属于优等级,有36.07%的人认为属于良等级,有22.25%的人认为属于中等级,有11.50%的人认为属于合格等级,还有5.96%的人认为属于差等级。根据隶属度最大原则,这种使用舵机为驱动方式的机械臂设计时主要性能指标属于良等级。
同理,可求出经济性指标的综合权重:W2=(0.525 9,0.28,0.131 9,0.062 2),

表5 指标权重及其一致性检验
最终的评价结果为:B2=(0.2868,0.3412,0.2720,0.086 8,0.013 2)。
适应性指标的综合权重为:W3=(0.745 4,0.097,0.157 7),
最终的评价结果为:B3=(0.1843,0.3903,0.3903,0.025 5,0.009 7)。
其他指标的综合权重为:W4=(0.066 4,0.229 5,0.181 1,0.526 5),
最终的评价结果为:B4=(0.2152,0.3489,0.2781,0.133 0,0.024 8)。
则可以构造出总指标的模糊评价矩阵为:

得出,对主要性能指标、经济性指标、适应性指标及其他指标的总权重大小为:
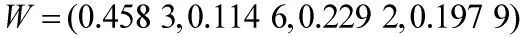
则最终的评价结果为:

由最终的评价结果可得,这款机械臂设计的最终结果表示有22.87%的可能性为优等级,有36.29%的可能性为良等级,有27.76%的可能性为中等级,有9.48%的可能性为合格等级,还有3.6%的可能性属于差等级。根据隶属度最大原则,此款使用舵机为驱动方式的设计机械臂最终结果属于良等级。
根据以上的方法,可以对多个机械臂设计方案进行综合评价,可排序出各个机械臂设计方案选择的优先次序,最终评选出最佳的设计方案。
3 结论
1)结果表明,本文提出的模糊熵权与AHP的综合评价方法,能有效解决难以定量的机械臂设计方案选择问题。
2)本文采用综合权重,即把熵权与层次分析法获得的权重结合起来,利用各个指标权重对所有指标进行加权,从而得到一组较为客观的评价结果,增强权重的可信度,使得确定的权重更科学、合理,从而确保了评判结果的可靠性。
3)利用熵权模糊综合评判方法对机械臂设计方案选择进行了总体评价,从而实现了复杂问题简单化,所选机械臂评价方案结果为良等级,评价结果具有一定应用价值,对多个方案选择时提供一种很好的评价体系,对快速选择方案提供了一定的参考意义。
