顾及有色噪声的卡尔曼滤波在多路径误差削弱中的应用
2019-03-14李川魏世玉刘星刘恋胡祝敏
李川,魏世玉,刘星,刘恋,胡祝敏
(1.重庆市地质灾害自动化监测工程技术研究中心, 重庆 401120;2.重庆大学 土木工程学院, 重庆 400044)
0 引 言
卫星信号在发射和传播过程中受环境等因素影响产生的反射信号将使直射信号能量发生衰减且相位产生延迟,这种现象称为多路径效应,由此产生的定位误差为多路径误差[1].多路径效应为一时空环境效应,其误差大小与卫星高度角、天线周围环境、反射面至接收机距离及天线性能等相关,难以构建准确误差模型对其进行改正.此外,多路径在基线两端不具有空间相关性,通过现有差分技术也很难对其进行削弱.分析表明:多路径效应对C/A码测量影响可达150 m,P码达10 m,对L1、L2载波造成的测距偏差最大分别为4.8 cm和6.1 cm[2].可见,多路径误差是GNSS高精度定位中主要误差之一[3].
国内外学者主要从4个方面研究多路径误差削弱方法:1) 选择良好的观测环境,如远离电磁干扰、大面积水面、高大墙体及山坡等[4].该方法简单有效,但实际观测中,某些观测点不可避免地位于观测环境较差的地方,故该方法存在一定局限性;2) 改善接收机天线硬件,如设置抑径板或抑径圈、天线极化法、天线增益法[1]等.该方法能在一定程度上削弱多路径误差,但改进的接收机往往体积大、造价高、不便于野外作业;3) 改进接收机信号处理,如窄相关技术[5]、多路径估计技术(MET)[6]、多路径消减延迟锁相环技术(MEDLL)[7]、CADLL技术[8]等,上述方法可有效削弱长延迟多路径误差,对于短延迟多路径误差,效果不显著;4) 观测数据后处理,如天线阵列法、反射信号计算法、信噪比法、多路径重复性方法[9]等,该方法可同时削弱长延迟和短延迟多路径误差,且数据处理方法灵活多样,但计算相对复杂、实时性较差.
经大量学者的研究,多路径误差削弱方法已取得长足进展,但在精密工程变形监测、海洋测绘、精密动态导航定位[10]等应用领域中, 多路径误差削弱一直是未能很好解决的问题.本文从观测数据后处理入手,以监测站坐标时间序列中多路径误差为研究对象,建立多路径误差状态空间模型,采用标准卡尔曼滤波和顾及有色噪声的卡尔曼滤波方法,从监测站第一天双差固定解的坐标残差序列中估计多路径误差序列,并根据多路径误差周日重复特性,利用第一天得到的改正模型对之后各天坐标序列进行改正,对比分析两种估计方法的优越性.
1 卡尔曼滤波
1.1 标准卡尔曼滤波
为解决线性高斯系统最优估计问题,卡尔曼等[11]于1960年提出一种递推式滤波算法,即卡尔曼滤波(KF),其递推公式如下[12-15]:
1)状态向量一步预报值及其方差矩阵:
(1)
(2)
2)状态向量滤波值及其方差矩阵:
(3)
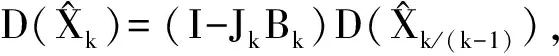
(4)
式中:Xk、Xk-1为状态向量;Φk/(k-1)为状态转移矩阵;Ωk-1为动态噪声;Γk-1为噪声耦合矩阵;Lk为观测向量;Bk为观测矩阵;D(Δk为观测噪声;Jk为滤波增益矩阵;具体形式为

(5)
3)滤波初始状态条件
(6)
KF假设系统在每一时刻的后验概率密度均是高斯型的,它用均值和方差对系统的状态进行描述.对于线性的、正态分布的系统状态估计问题,KF能够很好地解决.当过程噪声或观测噪声为有色噪声,滤波可能会出现发散现象.
1.2 顾及有色噪声的卡尔曼滤波模型
GNSS数据处理中,相邻历元间隔较短,多路径误差在历元间具有一定的相关性,致使系统过程噪声可能为有色噪声.如果把有色噪声当作白噪声处理,势必造成滤波估计精度下降,甚至滤波结果发散.因此,探索顾及有色噪声的卡尔曼滤波方法对提高多路径误差估计精度具有重要意义.

Γk/(k-1)Ωk.
(7)
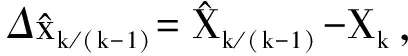
(8)

(9)
于是有:
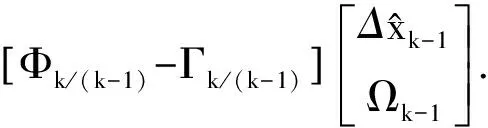
(10)

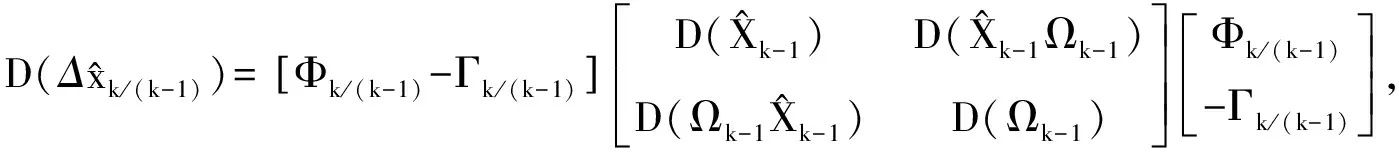
(11)
因为有:

(12)
则:
-(I+Jk-1Bk-1Γk-1)D(Ωk-1,k-2).
(13)
2 基于卡尔曼滤波的多路径误差估计
2.1 多路径误差状态空间模型建立

(14)
式中:Δt为相邻历元时间间隔;Ωk为系统在tk时刻的动态噪声.
记tk+1时刻有观测向量Lk+1=mk+1,则系统在tk+1时刻的观测方程可表示为
(15)
式中,Δk+1为系统在tk+1时刻的观测噪声.
2.2 滤波初始值的确定


(16)
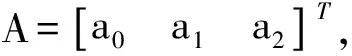

(17)
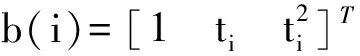
同时得拟合残差中误差:

(18)
拟合系数协方差矩阵:

(19)
取第N点处状态为初始状态,从N+1点处开始进行滤波递推,即:

(20)


(21)
式中,
载波相位测量中,相位测量精度一般为波长的百分之一,即σ=λ/100.由于双差观测值为4个独立观测值线性组合,双差解算结果的观测噪声方差阵为
D(Δk)=4σ2.
(22)
若将多路径误差在相邻历元间加速率的变化看作随机扰动项,有系统过程噪声[10]:
D(Ωk)=36Δt-6·D(Δk)
(23)
式(14)和式(15)构成了多路径误差估计的状态转移方程和观测方程.式(20)和式(21)构成了滤波初始值及协方差,式(22)和式(23)为系统观测噪声和过程噪声.
2.3 多路径误差估计实验设计
采用双差固定解算模型,逐历元解算出监测站各天的坐标序列并计算残差序列后,提取首日多路径误差模型后,将之后各天的坐标序列向前平移,利用相关系数最大法确定最佳平移时间,最后将第一天得到的多路径误差改正模型对平移后的坐标序列进行改正,以此削弱具有周日重复性的多路径误差.其详细步骤如下:
1)数据准备.利用GNSS接收机获取基准站和监测站连续多天同步观测数据.
2)数据解算.将观测数据导入到GNSS数据处理软件,采用双差固定解算模型,逐历元解算出监测站各天坐标序列.
3)计算残差序列.将监测站的已知坐标与解算出的坐标序列求差,得到监测站各天的坐标残差序列.
4)多路径误差估计.利用上述滤波估计模型,从第一天的残差序列中剥离出观测噪声的影响,得到多路径误差改正序列.
5)多路径误差改正.利用第4)步得到的多路径误差改正模型对之后各天坐标序列进行修正,以此削弱多路径误差.
3 实验分析
在距离约300 m的两楼顶分别架设GNSS接收机进行相对定位观测.选择视野开阔,观测条件良好处为基准站,如图1所示.选择周边多路径效应显著(北侧50 m处为高大建筑)处为监测站.同时,为更加凸显多路径效应的影响,人为地在监测站东侧1.5 m处设置一多路径反射面,监测站及周边环境如图2所示.

图1 基准站及周边环境

图2 监测站及周边环境
设置高度截止角10°,釆样间隔5 s.自2017年3月1日(doy60)开始连续观测至3月3日(doy62),选择双差固定解模式,逐历元解算出监测站各天N、E方向的坐标,同时得坐标残差序列,图3示出了监测站连续3天N方向坐标残差序列.由于基线长度非常短,差分解算后,坐标残差序列中主要包括不具有空间相关性的多路径误差和高频随机噪声.
为验证两种方法在多路径误差估计中的准确性和可靠性,分别利用标准卡尔曼滤波和顾及有色噪声的卡尔曼滤波,对监测站第一天(doy60)N方向的坐标残差序列进行滤波处理,得到两种多路径误差改正模型.图4和图5分别示出了两种模型的状态估计(包括多路径误差大小、变化速率及加速率).
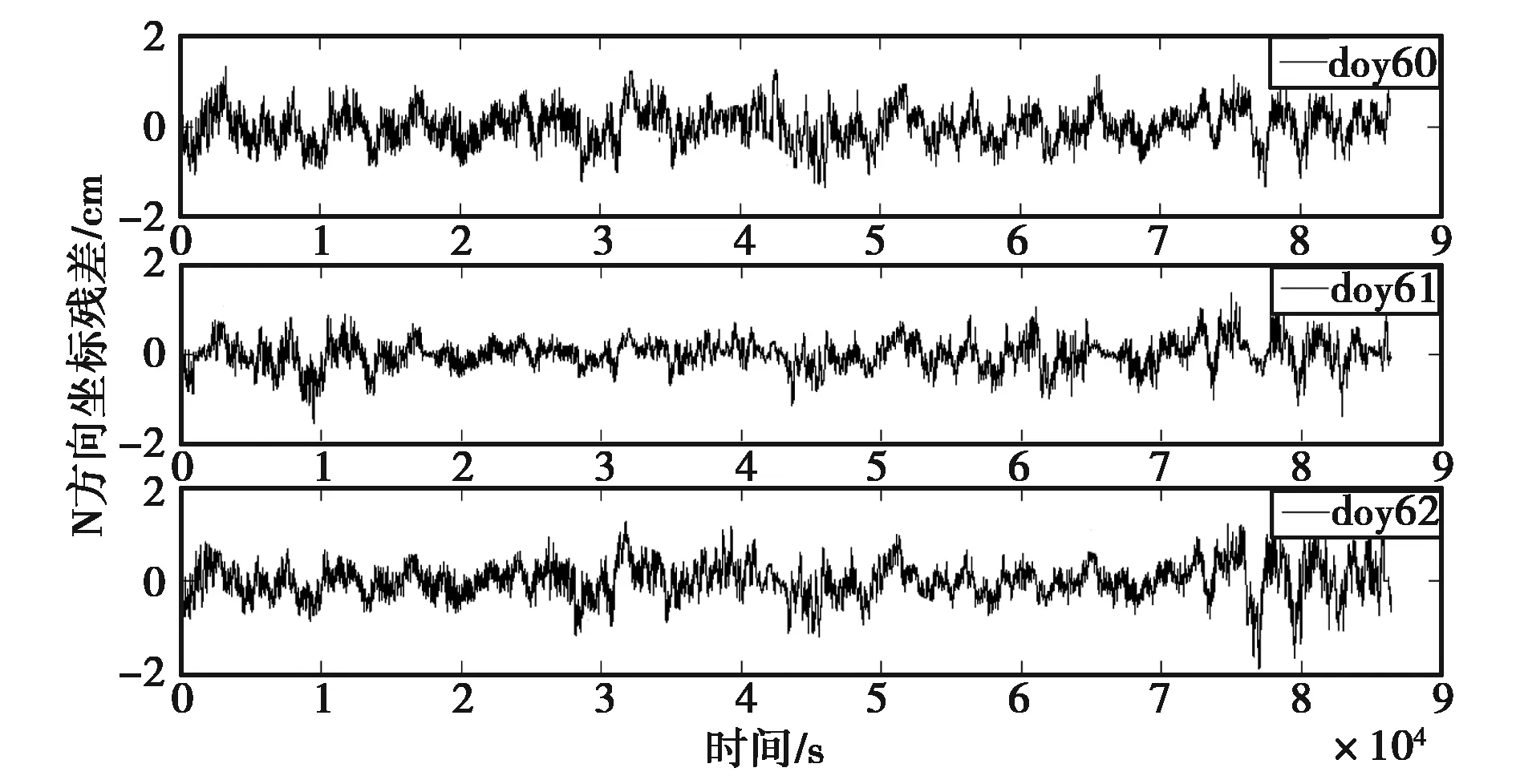
图3 监测站N方向各天残差序列
由图4及图5可知,多路径误差对N方向定位结果影响在2 cm以下,且具有一定的周期性和频率特征.另外,多路径误差在历元间存在一定变化速率和加速率(加速率较小),由此验证了多路径误差在历元间的时变特征.
最后,为分析两种模型估计出的多路径误差序列对原始坐标序列的改正效果,根据多路径误差的周日重复特性(相邻两天提前约236 s重复出现),对第二天和第三天坐标残差序列向前整体平移(平移时间为150~350 s),平移步长为1 s.每完成一次平移,将平移后的残差序列与前一天相对应的残差序列求互相关系数,以互相关系数最大所对应的平移时间来确定多路径重复出现的时间.表1示出了最大相关系数与对应平移时间的统计情况.

表1 最大相关系数与平移时间统计表

表2 坐标序列改正前后均方根误差统计cm
利用表2给出的最佳平移时间,对监测站第二天(doy61)和第三天(doy62)N方向的坐标序列进行平移,利用上述两种多路径误差改正模型对两天的坐标序列进行改正.图7和图8分别示出了两种多路径误差改正模型改正前后监测站N方向坐标序列.
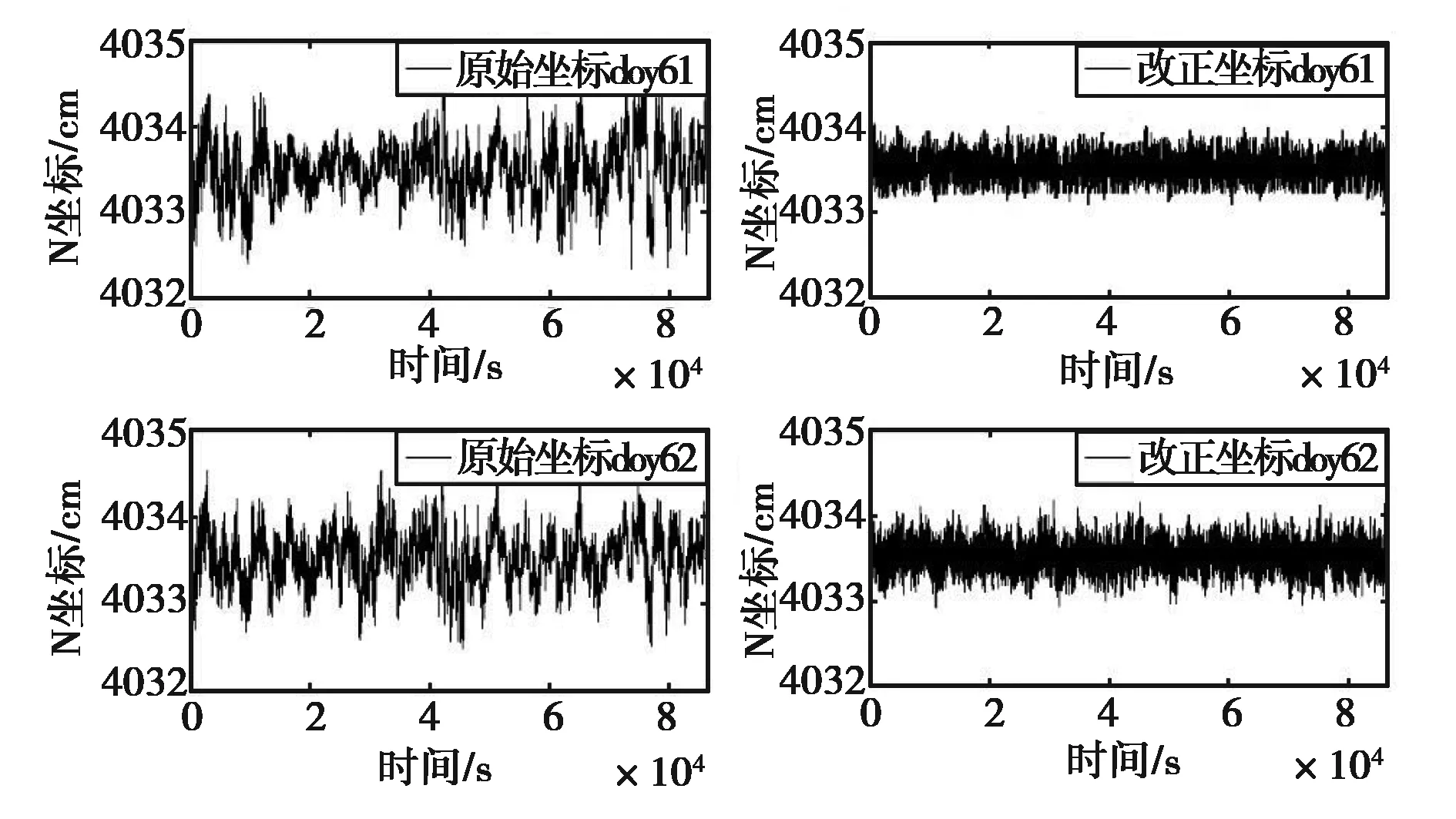
图7 标准卡尔曼滤波模型改正效果

图8 有色噪声卡尔曼滤波模型改正效果
由图7和图8可知,坐标序列在经多路径误差改正模型改正过后,具有时变特征的多路径误差得到大幅度削弱,改正后坐标序列中主要为观测噪声的影响.为分析两种多路径误差改正模型对之后各天坐标序列的改正效果,表2统计两种多路径误差改正模型改正前后坐标序列均方根误差.
由表2可知,经多路径误差改正模型改正后,坐标序列均方根误差得到大幅度削弱,且利用顾及有色噪声的卡尔曼滤波提取出的改正模型较标准卡尔曼滤波效果更优,另外,两种模型在第二天(doy61)改正后的均方根误差均小于第三天(doy62),由此说明多路径误差的周日重复特性会随着相邻天数的增加而减小.
多路径误差在历元间具有相关性,致使系统过程噪声在历元间也具有相关性.标准卡尔曼滤波假设过程噪声和观测噪声为不相关的高斯白噪声,因此利用标准卡尔曼滤对多路径误差进行估计时,很难保证其估计精度.实验表明,过程噪声为有色噪声时,基于有色噪声卡尔曼滤波估计方法优于标准卡尔曼滤波估计方法.同时结合多路径误差的周日重复特性,利用第一天多路径误差估计模型对之后各天坐标序列进行改正,坐标序列均方根误差得到大幅度削弱,且利用顾及有色噪声的卡尔曼滤波提取出的改正模型较标准卡尔曼滤波效果更优.
4 结束语
本文以坐标残差序列中多路径误差为研究对象,从观测数据后处理入手,采用卡尔曼滤波和顾及有色噪声的卡尔曼滤波方法对多路径误差进行研究,探讨多路径误差削弱方法.得出如下结论:
1)建立了多路径误差状态空间模型.根据多路径误差在历元间的时变特性,以多路径误差大小、变化速率、加速率作为状态变量,建立多路径误差状态空间模型,利用标准卡尔曼滤波及顾及有色噪声的卡尔曼滤波从双差固定解的坐标残差序列中估计出多路径误差.
2)顾及有色噪声的卡尔曼滤波误差估计方法效果要优于标准卡尔曼滤波.其主要原因是多路径误差在历元间具有相关性,致使过程噪声在历元间也具有相关性.标准卡尔曼滤波假设过程噪声和观测噪声为不相关的高斯白噪声,因此利用标准卡尔曼滤波对多路径误差进行估计时,很难保证其估计精度.
3)多路径误差改正方法.本文以GPS载波相位测量中的多路径误差为研究对象,利用上述多路径误差估计方法从监测站第一天的坐标残差序列中估计出多路径误差,并根据多路径误差的周日重复特性,对之后各天的坐标序列进行改正,以此削弱多路径误差的影响. 但多路径误差的周日重复特性是建立在监测站周边环境不变或者变化很小的基础上,因此本文的研究方法仅适用于测站周边环境保持不变或者变化很小的情况,如水库大坝、滑坡及高大建筑物等的变形监测.
