改进的平方根UKF在再入滑翔目标跟踪中的应用

2019-03-14叶泽浩毕红葵谭贤四曲智国张裕禄

宇航学报 2019年2期

叶泽浩，毕红葵，谭贤四，曲智国，张裕禄，程杨

(空军预警学院，武汉 430019)

0 引言

临近空间通常指海拔在20～100 km的高空[1-3]；临近空间高超声速飞行器指飞行于临近空间，飞行马赫数大于5的飞行器[4-5]。其具有飞行速度快飞行距离远，机动能力强，轨迹形式复杂多变等特点[6]。这对于该类目标的跟踪提出了严峻的挑战。

由于临近空间飞行器的运动状态相互之间、状态与观测量之间存在严重的非线性关系，因此需要用非线性滤波技术来得到其状态变量的最优估计[7]。目前，普遍应用的非线性滤波方法有：扩展卡尔曼滤波(EKF)以及无迹卡尔曼滤波(UKF)。文献[8]针对助推—滑翔飞行器提出了一种基于空气动力模型的扩展卡尔曼跟踪算法，该算法具有较好的跟踪精度，且可以有效估计助推—滑翔弹道的机动参数。文献[9]针对高超声速滑翔目标提出了一种基于气动力模型的交互多模型(IMM) EKF跟踪算法，当目标发生机动时，该算法具有更强的适应性和鲁棒性。但是EKF存在自身的理论缺陷：对于强非线性系统，EKF存在滤波性能极不稳定，甚至发散的问题；其在线性化处理时需要计算雅克比(Jacobian)矩阵，计算过程繁琐复杂且容易出错[10-12]。UKF则不需要计算Jacobian矩阵，在相当运算量下具有估计精度和鲁棒性更高等优点[13]。但是UKF需要对协方差矩阵进行Cholesky分解，这要求协方差矩阵必须为对称正定矩阵。文献[14]则提出了一种平方根UKF滤波方法，利用协方差的平方根代替协方差参加递推运算，从而解决了由于协方差矩阵负定而不能求其平方根的问题，同时还提高了滤波精度。文献[15]将平方根UKF用于航天器的测角导航系统中，相比于传统的EKF和UKF，具有计算速度快、稳定性好、导航精度高等优势。

本文根据临近空间高超声速目标的特点，采用了气动力模型，并进行了变换；同时将平方根UKF滤波算法应用到此类目标跟踪中，并对其从权系数和sigma点的选取、平方根矩阵的分解方法以及在协方差矩阵中引入稳定因子三方面进行了改进。该算法能在保证较高滤波精度和稳定性的同时大大减少了计算量加快了计算速度。

1 再入滑翔目标系统模型

设非线性系统的状态方程和量测方程：

(1)

式中：x为n×1维状态变量，f(x)为系统的非线性状态方程，z为m×1维观测向量，h(x)为非线性的测量方程；wk为过程噪声，Vk为测量噪声，且wk及Vk均为均值为零协方差矩阵分别为Qk和Rk的高斯白噪声。

1.1 系统状态方程

对此类目标，通过动力学来建模，可以较好的匹配其运动特性，达到精确稳定跟踪的目的。

在雷达站ENU(East north-up)坐标系下，传统的空气动力学模型可以表示为[16]：

(2)

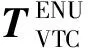
(3)

(4)

f(xk)=

(5)

wk=[wx,wy,wz,wvx,wvy,wvz,wd,wt,wc,wM]T，式中wx,wy,wz,wvx,wvy,wvz,wd,wt,wc,wM均为零均值高斯白噪声。

式中μ为地球引力常数；ω为地球自转速度，B为雷达站所在纬度，R0为地球半径，r为目标地心距。

1.2 系统观测方程

雷达的观测量建立在雷达地面球坐标系内，位置信息主要由观测距离d，俯仰角β和方位角θ三个参数进行描述。由上可得，系统的状态方程式建立在雷达地面直角坐标系内。因此，需要对雷达的观测量进行转换至直角坐标系下的位置坐标。用转化后的间接观测量来替代实际的观测量不仅可以与状态量实现统一还能大大简化运算。

目标的位置矢量与观测距离d，俯仰角β和方位角θ有如下关系：

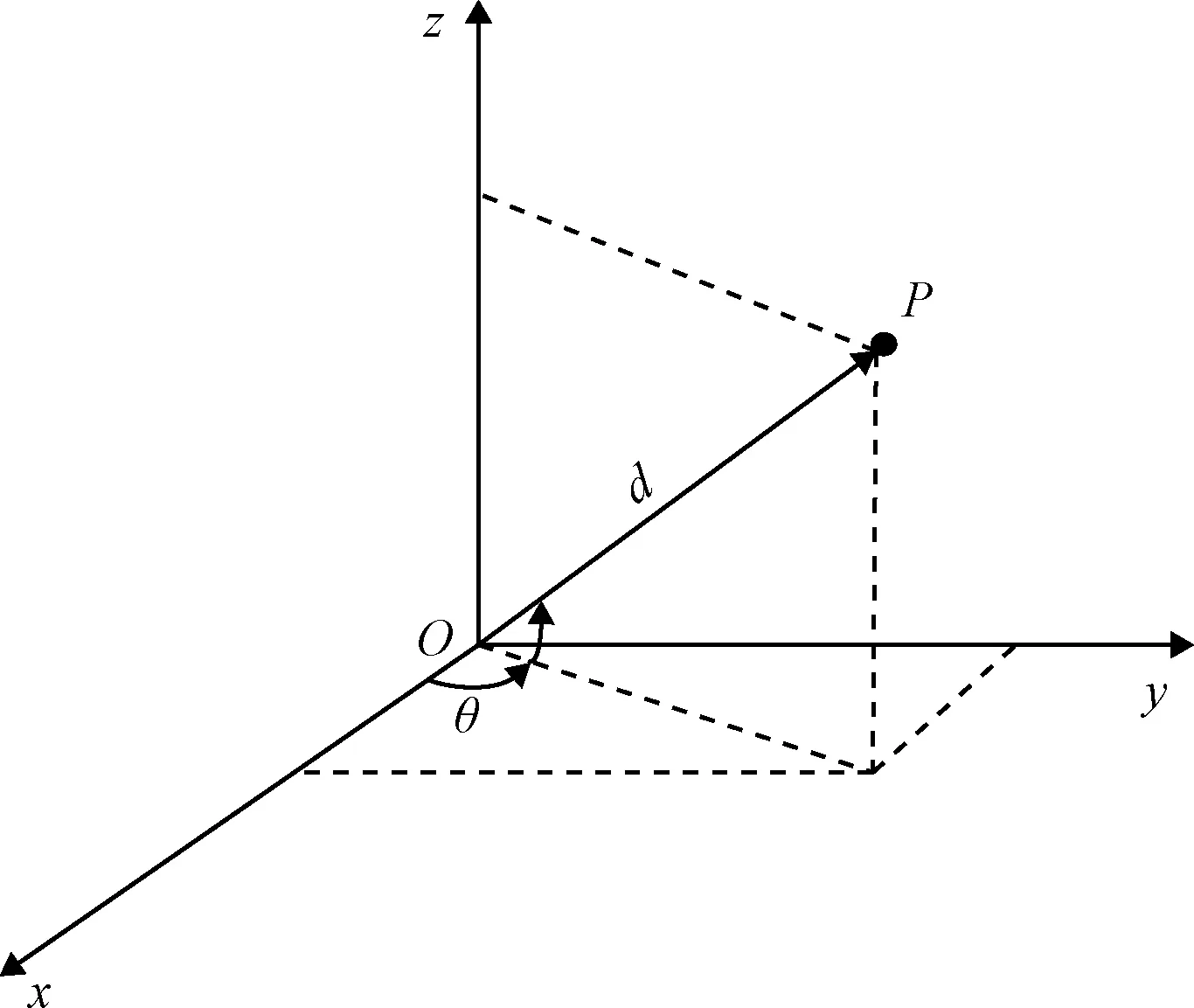
图1 转换关系示意图Fig.1 Schematic diagram of conversion relationship

则可得：

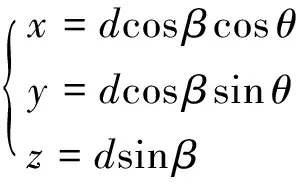
(6)

将位置x、y、z作为间接观测量来代替实际观测量r、θ和β，可得伪观测方程为：

(7)

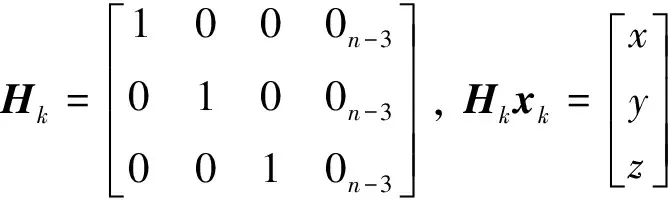
此时，还需要对观测协方差矩阵进行转换，假设观测距离标准差为σd，方位角和俯仰角标准差为σθ和σβ，则对应的协方差矩阵为：

(8)

则根据协方差传播理论可得转换后的观测协方差矩阵为：

(9)

(10)

2 平方根UKF滤波算法的改进

2.1 标准的平方根UKF滤波算法

(11)

(12)

式中，“Fchol(·)”表示Cholesky分解。

2)sigma点的计算选取：

(13)

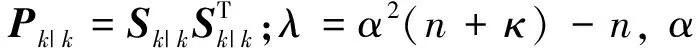
3)权系数的计算选取

(14)

式中，γ≥0为一个与状态的先验分布信息有关的参数，调节γ可以提高协方差矩阵的精度。对于高斯分布来说，γ=2是最优的。

4)时间更新：

(15)

(16)

(17)

(18)

式中，“Fqr(·)”和“Fcholupdate(·)”分别表示QR分解和Cholesky分解一阶更新。

5)量测更新

(19)

(20)

(21)

(22)

(23)

6)滤波结果更新

(24)

(25)

U=KkSz

(26)

Sk+1|k+1=Fcholupdate(Sk+1|k,U,-1)

(27)

2.2 算法的改进

2.2.1球形无迹变换选取权系数和sigma点

标准的平方根UKF算法中的sigma点和权系数的计算选取，涉及参数种类多，各参数调节过程较为繁琐；而且，对于n维的状态向量无迹变换需要2n个sigma点，而球形无迹变换只需要(n+2)个sigma点就能达到一般无迹变换的精度和数值稳定度，其对于权系数的选择也比较容易确定。因此，采用球形无迹变换选取权系数和sigma点能在保持数值精度和稳定度的同时大大加快计算速度。

1)权系数的选择：

W0∈[0,1)

(28)

(29)

则以式(28)和(29)对式(14)进行替换。

2)计算sigma点：

(30)

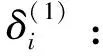
(31)

(32)

则以式(30)、(31)和(32)对式(13)进行替换。

2.2.2平方根矩阵的分解改进

在标准的平方根UKF算法中对于求向前一步预测的估计协方差平方根Sk+1|k由式(17)与式(18)给出，但按式(18)实际的可表达为：

(33)

运用cholupdate更新协方差矩阵有一定的要求，其需要等式(33)的右边必须是正定的。

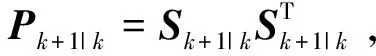
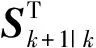
(34)

则进一步可令：

Sk+1|k=rT

(35)

根据向前一步预测的估计协方差矩阵计算公式：

(36)

即：

(37)

则由式(35)、(36)、(37)可直接推得到Sk+1|k的更新方程如下：

(38)

(39)

同理对于式(21)和(22)的量测估计协方差的平方根矩阵更新方程可以改为如下：

(40)

(41)

另外，在标准的平方根UKF滤波算法中对于状态误差协方差矩阵的更新按式(26)、(27)可实际表示为：

(42)

这要求式(42)的右边必须是正定的，但是在计算过程中，等式的右边由于含有相减的项，对舍入误差十分敏感，很容易因为舍入误差的积累，使结果失去正定性。因此还需对状态估计协方差的平方根矩阵作如下修改：

(43)

(44)

因此可以根据式(38)和式(39)的处理方法来得到改进的更新状态估计协方差的平方根矩阵：

(45)

(46)

2.2.3设计引入多重次稳定因子

由于平方根UKF中，sigma点的选取与协方差密切相关，因此本文设计了在协方差更新中引入多重次稳定因子Dk+1来直接调节协方差，其具体形式如下：

Pk+1|k+1=Dk+1(E-KkHk)Pk+1|k(E-KkHk)T·

(47)

其中，Dk+1=diag(d1,d2,…,dn)。则式(45)和(46)应进一步改为：

(48)

(49)

dn设为各稳定因子。对于有测量输入量的对应因子取为1，即不需要调节该位置的协方差，假若取值大于1，更容易发散，使增益估计出现奇异值；而对于没有测量输入量的取为0.95～1之间，来减少对应的协方差量，因为一开始这些参量的估计误差不大，只是恶性循环使误差呈现指数式增长，因此，对应的稳定因子的取值不需要过小，而且取值小了还会影响滤波精度。

3 仿真及分析

为了验证改进后的气动力模型和算法的有效性，分别设计了临近空间高超声速再入飞行器跳跃滑翔轨迹和平衡滑翔轨迹，如图2所示。

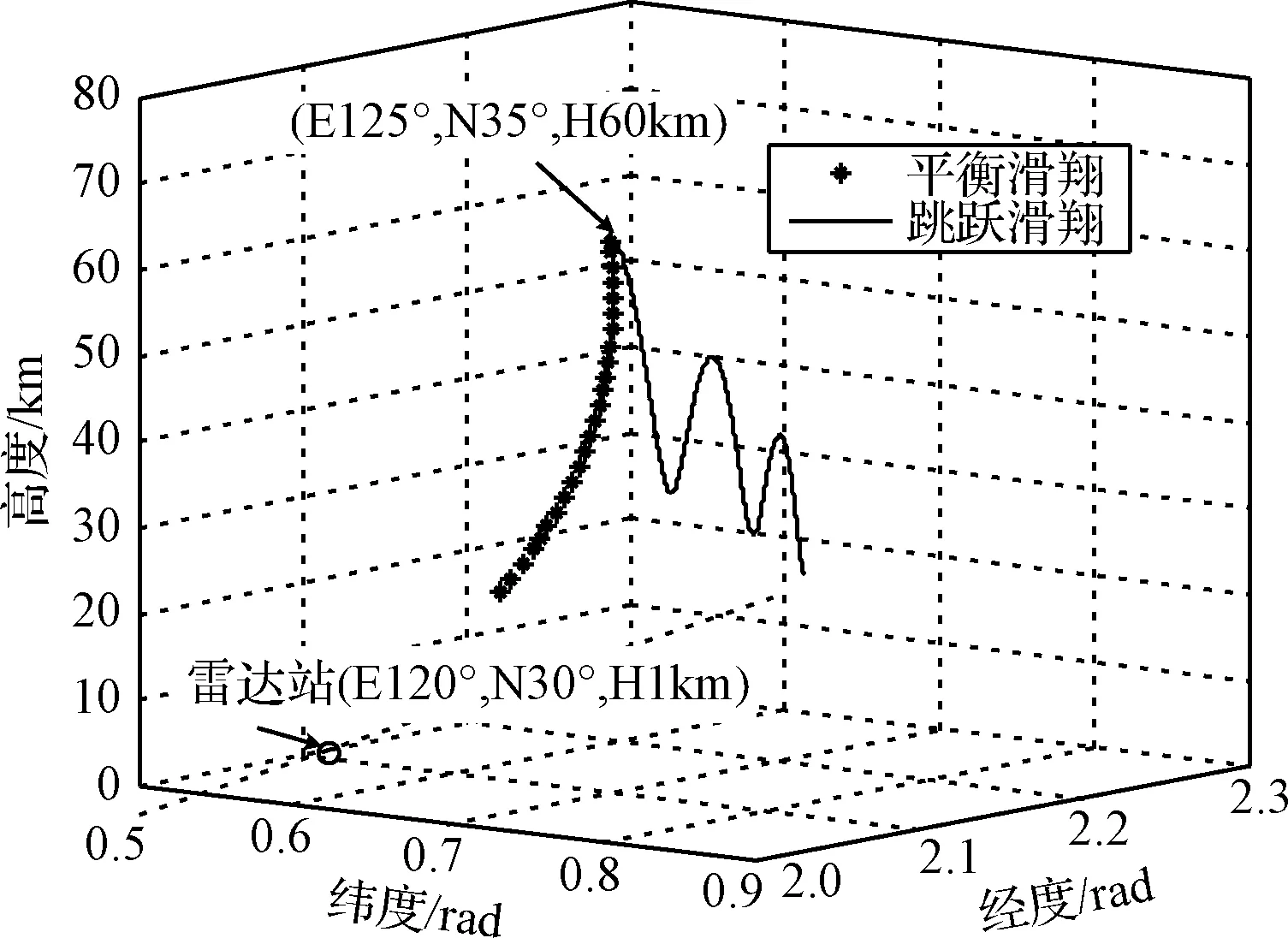
图2 目标再入轨迹仿真Fig.2 Target reentry trajectory simulation

将新气动力(new aerodynamic force)的ISR-UKF算法(NISR-UKF)、原气动力(traditional aerodynamic force)的ISR-UKF算法(TISR-UKF)、新气动力的SR-UKF算法(NSR-UKF)以及原气动力的SR-UKF算法(TSR-UKF)对上述轨迹进行跟踪滤波。设置仿真时长为500 s，跟踪采样间隔0.1 s，雷达测距精度100 m，测角精度0.0015 rad，进行50次蒙特卡洛仿真，结果如下。

其中在仿真中，NSR-UKF和TSR-UKF两种算法，需要设定合适的初始状态值、初始过程噪声和初始协方差才能正常运行出结果，即未出现奇异值。因此这两类算法的可靠性比较差。而同时为了保证结果有效性，将NISR-UKF算法与NSR-UKF算法(状态变量都为十维)的初始值设置相同，将TISR-UKF算法与TSR-UKF算法(状态变量都为九维)的初始值设置相同；并且，由于他们的状态变量(无论是十维还是九维)，前六维都为位置量和速度量，因此，相对应的初始值设置都相同。

3.1 平衡滑翔轨迹的跟踪结果

图3 目标位置估计均方根误差Fig.3 Target position estimation root mean square error

图4 目标速度估计均方根误差Fig.4 Target speed estimation root mean square error

为了可以进一步定量地分析四种算法的性能，对仿真的各状态的RMSE估计结果做统计平均及算法的耗时情况进行比较，结果如下：

由图3和表1可以发现，在位置估计上四种方法均具有良好的估计精度、收敛性和稳定性。那是因为气动力模型与目标的运动特性匹配度比较高；而且平衡滑翔轨迹的轨迹相对较平缓，机动性较弱。但是还是存在较明显的优劣：算法NISR-UKF的估计精度最高，收敛性和稳定性也好于其他三个；表现最差的是TSR-UKF算法；算法TISR-UKF与NSR-UKF相当，但是前者还是略好于后者。由图4和表1都可以发现，在速度估计上，存在明显的优劣势，估计效果最好的是NISR-UKF算法，其次是TISR-UKF算法，之后是NSR-UKF算法，最差的是TSR-UKF算法。那是因为速度的估计精度与气动参数估计精度直接相关，而TSR-UKF算法无任何改进，其对于气动参数的估计误差较大。在算法的耗时上，NISR-UKF与TISR-UKF显著好于NSR-UKF与TSR-UKF，那是因为前两者采用球形无迹变换能显著减少计算量，加快计算速度；而同时因为新气动力的算法将状态量维度比原气动力方程又扩展了一维，因此在耗时上，NISR-UKF大于TISR-UKF，NSR-UKF大于TSR-UKF。

表1 各算法的跟踪性能比较Table 1 Comparison of tracking performance of each algorithm

3.2 跳跃滑翔轨迹的跟踪结果

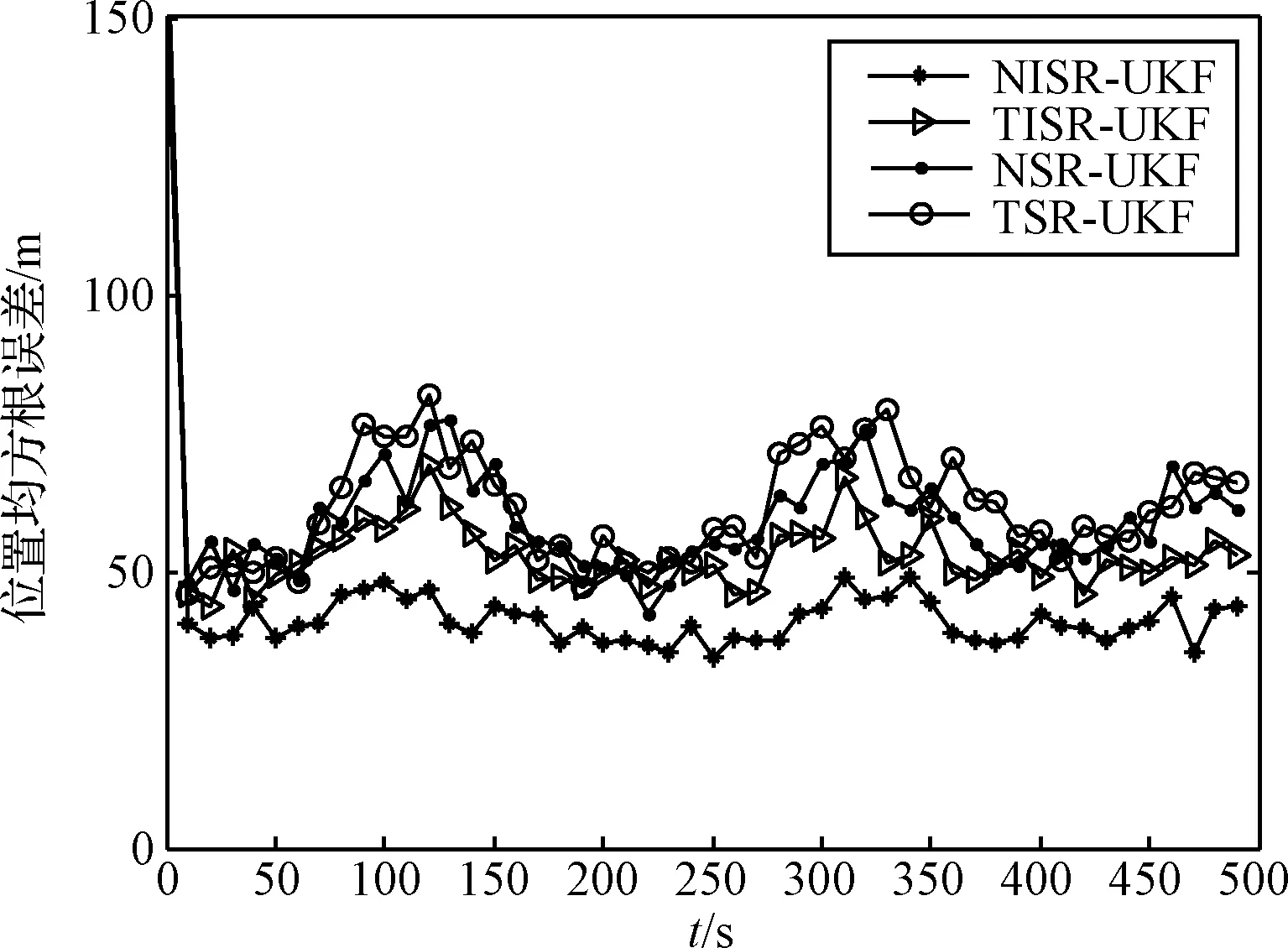
图5 目标位置估计均方根误差Fig.5 Target position estimation root mean square error

图6 目标速度估计均方根误差Fig.6 Target speed estimation root mean square error

为了可以进一步定量地分析四种算法的性能，对仿真的各状态的RMSE估计结果做统计平均及算法的耗时情况进行比较，结果如下：

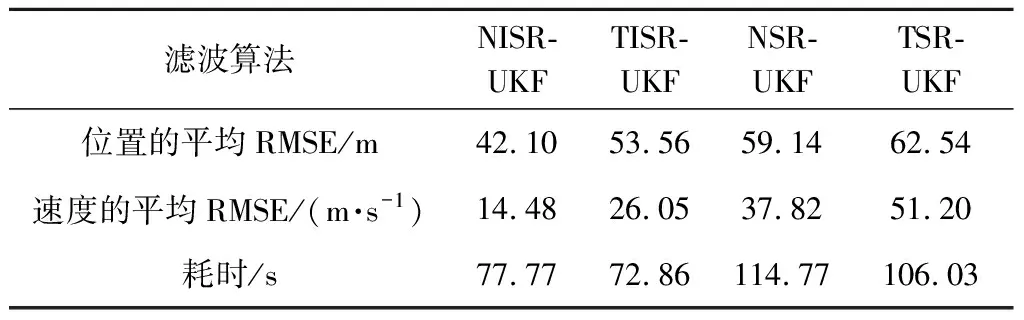
表2 各算法的跟踪性能比较Table 2 Comparison of tracking performance of each algorithm

由图5和图6以及表2可以发现，在位置估计和速度估计上，均存在三处波动起伏(100～150 s、300～350 s、500 s左右)，那是因为该跳跃滑翔轨迹存在跳跃机动，轨迹变化比较剧烈，尤其在100～150 s、300～350 s、500 s左右位于轨迹跳跃的最低点。但是，NISR-UKF的估计效果明显要好于其他三种，而且，总体走势较为平缓，体现了良好的跟踪性能。其次仍然是TISR-UKF算法、NSR-UKF算法，效果最差的仍然是TSR-UKF算法。在耗时上，与仿真1结论相同。

综上所述，对于再入滑翔轨迹，本文的气动力模型变换、引入的球形无迹变换、改进的平方根分解方法以及引入的稳定因子能不同程度地改善滤波性能，最主要是能避免奇异值问题的出现，算法的可靠性更强；而且引入的球形无迹变换还能显著提高滤波的速度。NISR-UKF算法无论在计算速度、滤波精度、收敛速度、稳定性以及可靠性上都具有良好的表现，仿真结果验证了算法的有效性。