复杂动态环境下无人飞行器动态避障近似最优轨迹规划

郭 行，符文星，付 斌，陈 康，闫 杰

(西北工业大学航天学院，西安 710072)

0 引 言

如何在复杂动态环境中利用探测信息规避各种障碍并高效完成飞行任务是无人飞行器路径规划质量的重要衡量标准。

目前，无人飞行器避障轨迹规划主要分3类：第一类为通过几何方法进行路线规划，保证飞行路线与障碍没有交集，但曲率限制不直接对应控制约束，代表方法有PH[1]、dubins等[2]；第二类为将避障问题融入性能指标，依据Hamilton原理求解，代表方法有比例导引法[3]、模型预测控制等[4-5]；第三类为依据概率论进行避障，通过计算概率分布密度函数确保避障概率超过门限值，但其依赖大量数据样本或者近似概率分布函数[6]。

针对动态避障近似最优路径规划问题，本文采取第二类方法。Han等[3]基于传统比例导引法推导避障飞行制导律，然而没有解决过载发散缺点；Singh[4]依据模型预测控制设计自主规避轨迹，但忽略控制约束且算法效率低；Gagnon等[5]依据模型预测控制研究无人飞行器避障轨迹，但情形较为简单；Watanabe等[7]通过给定中间点研究能量最少避障制导律，但中间点难以确定；Keith等[8]设计混合整数线性规划(MILP)迭代算法，完成固定区域避障；Smith等[9]利用直接正交配置法求解最优避障走廊，但结果有概率性；Snyder等[10]设计轨迹生成、轨迹跟踪和时间协调的协作任务系统完成避障，但不具最优性；冯丽程等[11]基于有限时间滑模变结构控制与人工势函数实现航天器安全交会，但障碍运动形式较为简单；羊帆等[12]基于障碍物伪距离技术实现避障规划-跟踪一体化控制，但仅描述障碍形状，障碍运动描述比较简单。

本文在以往无人飞行器规避简单障碍基础上进一步研究其规避动态障碍近似最优路径规划。首先依据OMPSP算法解决终端约束与控制约束，然后提出松弛变量与滑模变结构的组合方法应对安全避障的不等式约束，最后采取RHDDP算法进行轨迹优化，得到动态避障近似最优轨迹。

1 无人飞行器动态避障问题描述

本文研究二维平面动态避障轨迹规划，然而其可扩展至三维情形。假设无人飞行器匀速率运动，其运动学模型和控制约束为：

(1)

|a|≤amax

(2)

式中,(x,y)为无人飞行器前向和横向位置,V和γ分别为其速度和轨迹倾角,a和amax分别为其转弯加速度和最大转弯加速度。

对于动态障碍，其典型运动模式如下：

1)匀速直线运动

该运动形式下，动态障碍的运动学为：

(3)

式中,(xo,yo)为动态障碍前向和横向坐标,Vo为其速度,γo为其轨迹倾角。

2)斜向匀速简谐运动

该运动形式即为横向简谐运动与斜向匀速直线运动的叠加，可以描述为：

(4)

式中,Vo为动态障碍斜向匀速直线运动速度,γo为其斜向匀速直线运动轨迹倾角,Ao为其简谐运动幅值,fo为其简谐运动频率,其它变量含义与式(3)中对应相同。

3)匀加速转弯运动

该运动形式下，动态障碍的运动学为：

(5)

式中，ao为动态障碍转弯加速度，其它变量含义与式(3)中对应相同。

为保证对动态障碍的安全规避，无人飞行器需要满足以下不等式约束：

(6)

式中，Ds为安全距离。

假设动态环境中无人飞行器终端约束为(x,y,γ)f=(xf,yf,γf)，由于终端时刻难以确定，因而对于此“有限时间”，本文以坐标x代替时间t作为自变量，同时引入约束：

(7)

无人飞行器动态避障问题的数学描述为：

(8)

(9)

式中,h为步长,下标k表示k时刻状态值。安全避障的不等式约束具体为：

(10)

无人飞行器状态、控制和终端约束分别为：

(11)

|ak|≤amax

(12)

(13)

式中,N为总步数，满足：

N=(xf-x1)/h+1

(14)

式中,x1为初始时刻无人飞行器x坐标。轨迹规划的性能指标为能量最少，即：

(15)

由此，无人飞行器轨迹规划状态向量xk=(tk,yk,γk,xo1k,yo1k,xo2k,yo2k,γo2k,xo3k,yo3k)T，控制向量uk=ak，输出向量yk=(yk,γk)T。相关基本运动参数如表1。

2 无人飞行器动态避障近似最优轨迹规划

2.1 初始轨迹生成

MPSP[13-14]收敛速度快、精度高、算法简便，其优化算法同时解决控制和终端约束[15-16]，因此本文用其进行初始轨迹生成。

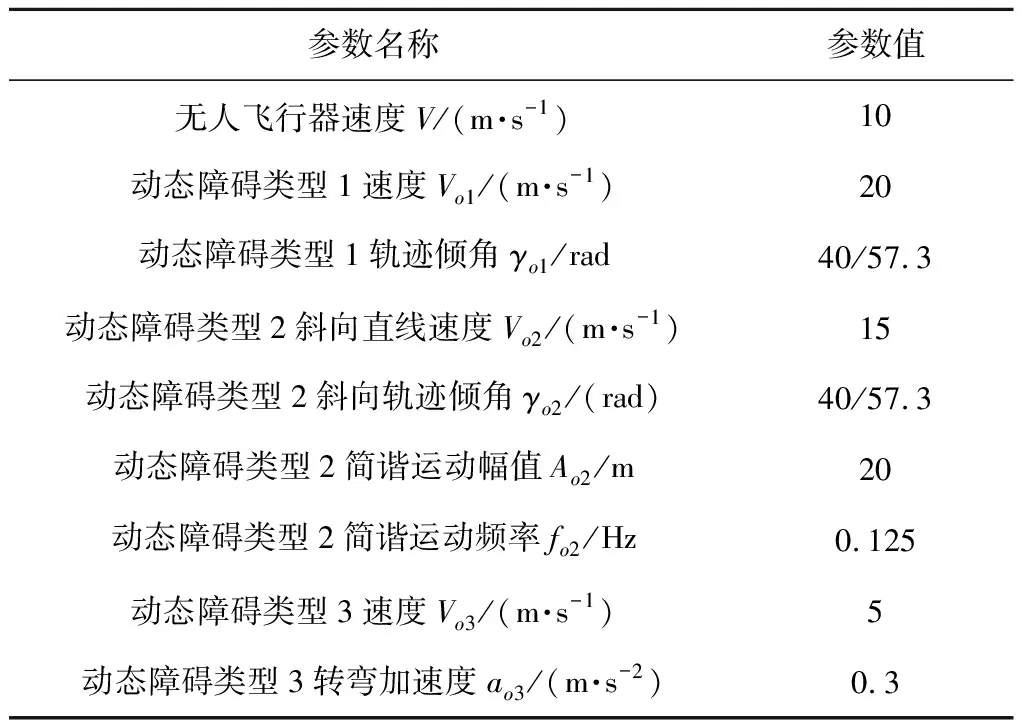
表1 无人飞行器和动态障碍基本运动参数Table 1 Basic kinetics parameters for the UAV and dynamic obstacles

假设系统数学模型和期望终端状态为

(16)

(17)

最优问题的性能指标为能量最少，即：

(18)

式中,Rk为正定权重矩阵。则最优控制为：

(19)

为保持算法简便并保证收敛速度，依据文献[16]，在收敛后根据控制约束更新控制量，并同时自适应调整Rk，促进下一次收敛时满足控制约束。初始轨迹记为(x0,u0)。

2.2 动态障碍规避轨迹设计

1)规避部分设计

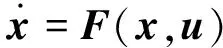
E(x;t)≤0

(20)

(21)

连续对式(21)进行求导直至出现控制u：

(22)

式中,上标表示求导阶数。则控制u为：

(23)

由此系统状态方程转化为

(24)

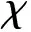
(25)

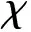
(26)

式中,k1>0,ε1>0,δ1>0。由式(25)、式(26)有：

-cm-1χ(m-1)

(27)

i=1,2,3

(28)

式中,ps≥1为安全系数。对上式连续求导：

(29)

式中,

(30)

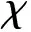
(31)

并且松弛变量子系统可以描述为：

(32)

式中,

(33)

由式(26)、(31)、(32)联立可得：

(34)

将无人飞行器规避区域划分为预警规避区(橙色区域)、执行规避区(紫色区域)和绝对规避区(红色区域)，如图1所示。

图1 无人飞行器规避区域划分示意图Fig.1 Partition of UAV’s avoidance region

(1)无人飞行器进行预警规避的条件为：

(35)

(36)

式中,

(2)无人飞行器进行执行规避的条件为：

(37)

(4)无人飞行器进行绝对规避的条件为：

(38)

(39)

当无人飞行器需要同时规避多个障碍时，将其统一为单个障碍并扩大安全距离。以同时规避三个障碍为例，则有：

(40)

2)恢复部分设计

依据上述方法可以实现避障，然而避障完成后仍需轨迹恢复。因此，本文设计滑模面s2将轨迹恢复至初始轨迹，即：

s2=d1(tk-tk 0)+d2(yk-yk 0)+(γk-γk 0)

(41)

由于避障消耗额外的时间，因此取d1=0,d2>0。对于s2仍采取指数趋近律，并以饱和函数sat(·)代替符号函数：

(42)

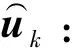
ε2sat(s2)]=ak 0-V2cosγk[d2(tanγk-

tanγk 0)+k2s2+ε2sat(s2)]

(43)

在轨迹恢复过程中，控制量uk仍需确保安全规避，因而其选择标准设置为：

(44)

综合轨迹设计部分(1)和(2)可得规避轨迹，记为(xc,uc)。

2.3 动态障碍规避轨迹优化

2.2节不仅设计规避轨迹，同时也得到避障的危险区域，因此轨迹优化性能指标为：

(xN-xf)TQN(xN-xf)

(45)

式中，QN、Qk为非负定权重矩阵。在危险区域内Qk较大，保证动态规避。由于RHDDP[19-20]搜索能力强、收敛速度快、收敛精度高，因此依据此算法进行优化。

对于系统描述式(16)，定义逆序控制量Uk≜{uk,…,uN-1}，定义剩余性能指标为：

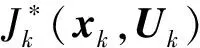
(46)

则最优剩余性能指标为：

(47)

令G(xk,uk)=l(xk,uk)+Vk+1(F(xk,uk))，则其在(xk,uk)附近的变分为：

G(xk+δx,uk+δu)≈G(xk,uk)+(Gx)kδx+

(48)

式中：

(49)

根据变分法可得：

(50)

将式(50)代入式(48)可得：

(51)

Vk(xk)在xk附近的变分可表示为：

(52)

由式(51)、(52)可得以下近似关系：

(53)

式(49)和式(53)构成RHDDP逆向优化递推方程。其前向优化递推方程为：

(54)

式中，0<ρ≤1为算法可调节系数。

3 动态避障轨迹规划仿真校验

仿真条件如表2所示。

3.1 初始轨迹生成仿真

通过OMPSP算法，初始轨迹进行8次迭代后收敛，无人飞行器终端状态为(tN,xN,yN,γN)=(30.50,300.00,50.05,9.33×10-7)。

由仿真结果可得：OMPSP算法能够在满足控制约束和终端约束情况下高效完成能量最少的近似最优初始轨迹生成。

3.2 规避轨迹设计仿真

规避轨迹仿真所得到的最终状态为(tN,xN,yN,γN)=(33.15,300.00,50.60,3.90×10-3)。

由仿真结果可得：动态避障方法能够同时规避多个动态障碍；控制量存在较大波动；规避轨迹显著消耗能量并增加飞行时间。

表2 相关仿真参数值Table 2 Values of relevant simulation parameters

图2 无人飞行器初始飞行轨迹Fig.2 UAV’s initial flight trajectory

图3 初始轨迹控制量随时间变化曲线Fig.3 Control input’s profile for initial trajectory

图4 无人飞行器动态规避飞行轨迹Fig.4 UAV’s avoidance flight trajectory

图5 规避轨迹控制量随时间变化曲线Fig.5 Control inputs’ profile for avoidance trajectory

3.3 轨迹优化仿真

无人飞行器终端状态为：(tN,xN,yN,γN)=(31.92,300.00,50.01,-1.80×10-3)。

图8 无人飞行器优化飞行轨迹Fig.8 UAV’s optimized flight trajectory

图9 优化轨迹控制量随时间变化曲线Fig.9 Control profiles for optimized trajectory

图10 无人飞行器与各障碍距离变化曲线Fig.10 Profiles for the distances between UAV and obstacles in optimized flight trajectory

由以上仿真结果可得如下结论。

优化轨迹仍能规避动态障碍且能量消耗明显减少；优化轨迹综合考虑动态避障约束、能量最少性能指标和终端状态约束，是促使式(45)性能指标最小的近似最优轨迹。

3.4 算法计算效率说明

本文仿真平台为CPU：Inter(R) Core(TM) i5-3470，主频：3.2 GHz，内存：4 GB。程序运行耗时如表3。

表3 各个轨迹计算耗时情况表Table 3 Time consumption for each trajectory

根据表3，算法整体具备很高的计算效率，具备一定的在线实时规划潜力。

4 结 论

本文针对无人飞行器复杂动态环境下动态避障问题，创新地提出动态避障近似最优轨迹规划方法。它将动态障碍威胁、控制约束、终端约束等分解处理，依次设计初始轨迹、规避轨迹、优化轨迹以使最终飞行轨迹具备近似最优特性，并保证动态避障和满足各种约束。同时，本文算法简洁高效，充分利用各子算法优势。此外，本文动态障碍模型极具代表性，包含同时规避多个动态障碍的特殊情况，因此本文轨迹规划方法具有很强的应用性，为将来无人飞行器避障轨迹规划提供了新的思路与借鉴。