钢轨模态阶数对高速铁路轮轨高频动力响应的影响研究

韦 凯 王 平 牛澎波

(西南交通大学， 成都 610031)

我国高速铁路建设经过多年的创新发展，成功建立了时速250 km与350 km两个高速铁路建造体系[1]。随着行车速度的提高，再加上轨道不平顺和轨道结构的变形[2]，轮轨高频振动也逐渐加剧。

为了分析轮轨系统的高频振动特性，国内外学者从轨道结构的多个方面做了大量的相关研究。徐志胜[3]等人通过对高速铁路车辆-轨道耦合振动仿真分析，对比了Timoshenko梁与Euler梁模型对轮轨高频振动仿真结果的影响。高建敏、翟婉明[4]等人分析了轨道几何不平顺波长变化对高速车辆系统动力响应影响。刘子煊[5]将描述扣件胶垫幅变相关的Berg摩擦模型和频变相关的分数阶Zener模型应用到车辆-轨道耦合系统动力学模型中，对比分析了胶垫的幅频变特性对轮轨系统动态响应的影响，但是其动力仿真计算模拟的钢轨模态阶数未能准确地反映扣件胶垫幅频变特性在中高频的动力特性，导致轮轨系统的动力响应结果偏大。

随着高速铁路行车速度的提高，为更准确地分析轮轨高频动力响应，本文选用能够更准确描述扣件胶垫高频动力特性的幅频变模型模拟其动态力学特性，对比计算了高频随机振动激励下钢轨模态阶数对动力仿真计算结果的影响，为准确的分析在车辆-轨道耦合系统高频随机动力学中轮轨系统的动态响应提供参考依据。

图1 扣件胶垫幅频变动力性能的力学本构模型图

1 扣件胶垫幅频变特性的本构模型

扣件系统中的扣件胶垫属于粘弹性材料(橡胶材料)，主要表现为与温度、激振频率以及激励振幅的非线性特性[6]。高速铁路轮轨系统振动为宽频振动，扣件胶垫变形最大应变可达到30%～40%，这样的变形已经超出了橡胶材料的线性应变范围，采用线性模型不能准确表征其动力性能，需在高速铁路扣件系统中采用更精确的模型去描述扣件胶垫的动力特性。扣件胶垫幅频变动力性能的力学本构模型，如图1(a)所示，模型中包括摩擦元件和粘弹性元件，总应力分为摩擦力和粘弹性力，用公式表示为：

F=Fve+Ff

(1)

式中：Fve——频变相关的粘弹性力;

Ff——幅变相关的摩擦力。

1.1 频变相关性力的数学描述

本文采用的分数阶Zener模型能够用4个参数有效描述扣件胶垫的频变动力性能[7]，其模型图如图1(b)所示，时域本构方程为：

(2)

式中:Fve(t)——扣件胶垫的粘弹性力;

x(t)——扣件胶垫的位移;

α——分数阶数;

τ——高聚物松弛时间;

K0——当激振圆频率ω趋于0时的储能刚度;

K∞——当激振圆微率w趋于正无穷时的储能刚度。

通过进行傅里叶变换得模型的复刚度，表达式：

(3)

由式(3)可得到分数阶Zener模型与激振频率相关的储能模量与损耗因子。

(4)

(5)

式中：Δt——数值积分步长；

N——积分步数；

Ai+1——Grünwald系数。

Ai+1满足公式：

(6)

把式(4)、式(5)带入式(3)中，经化简得到扣件胶垫粘弹性力的表达式：

(7)

采用分数阶Zener模型计算每一个积分步的扣件支反力时，需计算所有时刻扣件胶垫的动态位移，随着积分步数的增加，会影响数据存储空间与计算效率。针对此问题Spanos等人指出，在积分计算时，只需求出当前时间步之前160步的位移，便能得到满意的结果[9]。基于此，本文在用式(7)积分计算时，当总积分步数小于160时，取N=N；当积分步数大于160时，取N=160。

从式(7)可以看出，分数阶数值积分不仅与当前积分步的值紧密相关，且整个积分过程中每一步的计算结果紧密相关，所以能更好地描述扣件胶垫的动力学特性。

1.2 振幅相关性力的数学描述

M Sjoberg[10]等人认为表现为振幅相关性的力主要是橡胶内部大分子运动之间的摩擦造成的，表现为摩擦力。这种摩擦力仅与振幅有关，与激振频率无关。本文对扣件胶垫中的摩擦力采用Berg摩擦模型进行表征，其表达式为：

(8)

式中：ffmax——扣件胶垫的最大摩擦力;

x2——摩擦力达到最大摩擦力一半大小时板的最大位移;

ffs——摩擦力；

xs——每次位移方向发生变化参考点的位移。

1.3 模型参数

文献[7]测试了Vossloh300型扣件系统的动态粘弹性动力性能。根据试验结果对幅变相关的Berg摩擦模型和频变相关的分数阶Zener模型的参数进行识别，得到较好的拟合结果。本文在其基础上采用同样的测试方法，在忽略扣件胶垫幅变特性的情况下，将实测力认为是粘弹性力，直接用分数阶Zener模型对实测数据进行拟合，用于对比分析有无幅变摩擦特性对扣件胶垫动力特性的影响。有无幅变摩擦特性对测试结果进行参数识别结果，如表1所示。

表1 幅频变模型参数识别结果

2 钢轨模态阶数对车辆-轨道垂向耦合系统高频振动的影响

本文以我国高速铁路无砟轨道为例，建立车辆-轨道垂向耦合动力学模型，如图2所示。其中车辆选用我国CRH380型高速客车，轨道选用长枕埋入式无砟轨道型式。以本文选用的分数阶Zener模型和Berg摩擦力模型计算扣件胶垫垂向支反力，计算分析了车辆-轨道垂向耦合系统高频随机振动仿真分析中钢轨模态阶数对轮轨系统振动响应的影响。

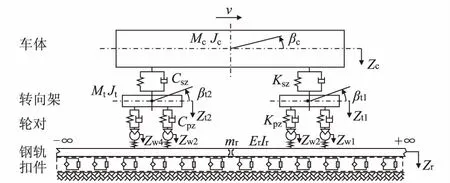
图2 车辆-轨道垂向耦合动力学模型图

2.1 计算工况

将高速客车简化为垂向具有10个自由度的车体模型，钢轨采用离散点支承的有限长Euler梁模型模拟。车辆和轨道的动力参数可参考文献[11]。在轮轨垂向耦合系统中，轮轨关系采用Hertz非线性弹性接触理论进行计算。

本文模拟高速客车运营车速350 km/h，轨道不平顺采用TB/T 3352-2014《高速铁路无砟轨道不平顺谱》进行仿真计算。该不平顺谱波长范围为2～200 m，激振频率最高只有48.6 Hz，远不能满足本文研究的频率范围，因此，将最短波长延伸到0.1 m，使激振频率最高达到972.2 Hz，然后再对轮轨动力响应进行计算。

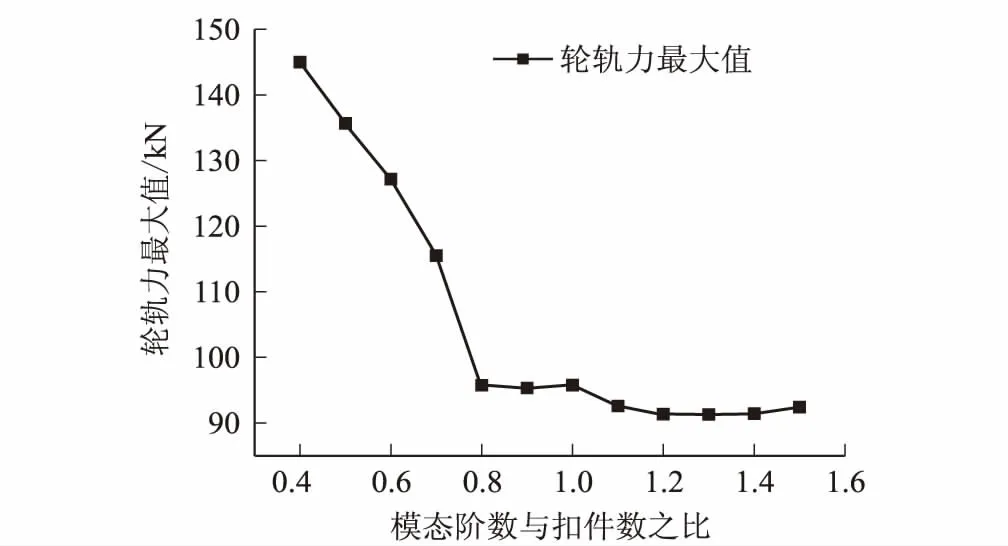
图3 不同模态阶数下的轮轨力幅值

2.2 模态阶数的选取

已有的文献研究结果表明，钢轨模态阶数与轨道扣件支点数Nf存在某种匹配关系[12]。本文先数值计算了钢轨模态阶数取扣件支点数的0.4～1.5倍范围内的轮轨力最大值变化曲线，如图3所示。从图中可以看出，当模态阶数从0.4Nf增大到0.8Nf时，轮轨力最大值从144.9 kN减小到了95.8 kN，减小幅度为33.9%；当模态阶数从0.8Nf增大到1.5Nf时，轮轨力变化幅值不大。因此，本文在动力仿真中，选取钢轨模态阶数0.5Nf、Nf、1.5Nf3种计算工况，对比分析不同钢轨模态阶数对轮轨系统仿真计算的影响。

2.3 模态阶数对轮轨系统仿真计算的影响

通过试算发现，动力仿真中钢轨模态阶数对车辆系统垂向振动产生的影响很小，因此本文着重研究3种钢轨模态阶数取值对轨道结构的动力响应。

(1)轮轨力对比

本文计算了3种钢轨模态阶数取值下轮轨力时/频域曲线，如图4、图5所示。从图4中可以看出，模态阶数取0.5Nf时，轮轨力时域计算值明显偏大，钢轨模态阶数取Nf和1.5Nf计算得到的轮轨力时域结果相差不大。在频域结果中，3种计算条件的轮轨力振幅值在1/3倍频程中心频率50 Hz以下的频带内几乎没有变化；而在60 Hz和800 Hz处的主频范围，钢轨模态阶数取0.5Nf计算的轮轨力振幅明显大于取Nf和1.5Nf，特别是在800 Hz处的高频范围，轮轨力振幅随模态阶数的取值变化更大。

图4 轮轨力时域图

图5 轮轨力频域图

(2)轮对垂向振动加速度对比

轮对垂向振动加速度时/频域计算结果对比，如图6、图7所示，从图中可以看出，钢轨模态阶数对其仿真结果的影响与轮轨力的影响相似。时域结果的加速度最大值随钢轨模态阶数的增大而降低；在频域中，高频范围的加速度振级随钢轨模态阶数的增大而减小。

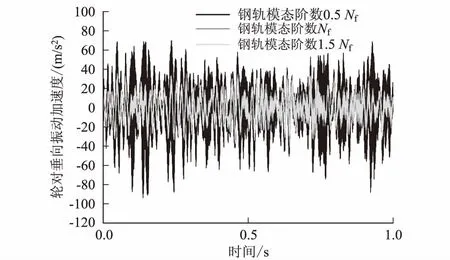
图6 轮对垂向振动加速度时域图

图7 轮对垂向振动加速度频域图

(3)钢轨垂向响应对比

3计算条件下的钢轨位移时程曲线，如图8所示，从图中可以看出，钢轨模态阶数对钢轨垂向位移最大值影响不大，且均未超过钢轨垂向位移基准值1.5 mm和最大允许值2 mm。由于粘弹性材料中内摩擦力的作用，在列车车轮驶过的时刻，钢轨位移没能立刻恢复到0 mm。

图8 钢轨垂向位移时域图

钢轨垂向振动加速度的时域仿真结果，如图9所示。从图中可以看出，钢轨模态阶数分别取0.5Nf、Nf和1.5Nf时，计算得到的加速度最大值分别为480.73 m/s2、302.28 m/s2、303.89 m/s2。对比发现钢轨模态阶数取值较小时，计算的钢轨振动加速度值偏大。钢轨垂向振动和加速度振级频域仿真结果，如图10所示。从图中可以看出，钢轨模态阶数的取值主要影响中心频率在400 Hz的钢轨垂向振动加速度振级。

图9 钢轨垂向振动加速度时域图

图10 钢轨垂向振动加速度振级频域图

3 结论

为更准确地分析高频激振条件下的高速铁路无砟轨道仿真计算的轮轨动力响应，本文通过采用扣件胶垫幅频变相关的Berg摩擦模型和分数阶Zener模型代替传统的线性模型，建立了高速铁路无砟轨道的车辆—轨道垂向耦合模型，在此基础上分析了钢轨模态阶数的取值对轮轨垂向系统时频域动力响应仿真结果的影响，得出以下主要结论：

(1)在轮轨动力响应的时域仿真结果中，钢轨模态取值较低会使轮轨力、轮对加速度和钢轨加速度计算得到的最大值偏大，随着钢轨模态阶数的取值增大，轨动力响应的最大值逐渐减小并趋于稳定，而钢轨的垂向位移变化不大。

(2)钢轨模态阶数取值主要影响轮轨系统在中高频范围的动力仿真结果。存在高频激振的情况下，钢轨模态阶数取值的不足，在中高频段的主频范围内使轮轨的动力仿真结果被放大。

(3)由时频域计算结果可知，为确保轮轨动力仿真得到更加准确的结果，需要根据激振频率的大小，对钢轨模态阶数进行合理的取值，对于激振频率较高的高速铁路动力仿真计算，本文建议将钢轨模态阶数最低取到轨道中的扣件个数。