时速400 km宽轨距高速铁路道岔设计关键技术

王 平 徐井芒 刘大园 庞 玲 姚 力

(1.西南交通大学， 成都 610031；2.中铁二院工程集团有限责任公司， 成都 610031)

道岔是实现列车转线运行的关键轨道设备，其结构与轮轨界面关系复杂、状态多变、病害繁多，集成了轨道结构的所有薄弱环节与技术特征。作为高精密度的机电一体化系统，道岔涉及铁道、机械、电气和控制工程等学科领域，是高速铁路建设发展中的核心技术之一。本文结合俄罗斯莫喀(莫斯科-喀山)高速铁路的技术需求，开展了时速400 km宽轨距高速铁路道岔的研制。

目前，世界上能自主设计、生产时速300 km及以上高速道岔的国家仅有德国、法国、日本和中国。法国Cogifer公司以有砟轨道高速道岔技术为主，其最高直向和侧向通过速度可达330 km/h和230 km/h，采用表面0.3 mm厚NiCr镀层和可调辊轮的减磨滑床板，减小转换阻力和不足位移。德国BWG道岔采用了缓圆缓线型及FAKOP动态轨距优化技术，研制了高弹性的橡胶垫板系统，形成了无砟轨道基础上的高速道岔成套技术，满足西班牙等国时速350 km高速铁路的建设需求。中国先后攻克了时速250 km和350 km的18号、42号和62号客运专线道岔理论研究，提出了适应客货共线运行需求的相离式半切线型，通过缩短轮载过渡范围优化了尖轨降低值，开发了特种断面翼轨和双肢弹性可弯心轨结构，并研制了道岔融雪和监测系统[1]。

各国高速道岔的设计及运营经验为莫喀高速道岔的设计提供了可供借鉴的成果。然而，世界范围内尚未有直接建设 1 520 mm宽轨距高速铁路的先例。尽管中国高速道岔的试验速度达460 km/h，但缺乏长期运营的经验，高速道岔设计尚未突破时速400 km的禁区且莫喀高铁为位于高纬度高寒地带的客货共线线路，道岔设计的结构复杂性、部件耐久性问题突出。为满足高速列车过岔安全性和平稳性的要求，需解决以下关键技术问题：(1)与运营条件相适应的道岔平面线型；(2)满足低动力设计要求的道岔轮轨关系和轨道刚度合理匹配；(3)适应跨区间无缝线路高平顺性的无缝道岔优化设计；(4)确保道岔可靠性与稳定性的转换设计。

1 道岔平面线型

为满足莫喀高铁高速道岔侧向容许通过速度120 km/h的要求，拟定了4种25号道岔线型方案，如表1所示。方案一中尖轨尖端和道岔末端的圆曲线半径为 2 800 mm，导曲线部分圆曲线半径为 2 230 mm，中间采用缓和曲线过渡；方案二和方案三均采用单圆曲线侧股线型，并采用相割量分别为10 mm和20 mm的半割型曲尖轨；方案四在方案三的基础上将道岔后长延长了3.047 m。

表1 宽轨距25号单开道岔平面线型参数对比

1.1 高速道岔运动学控制指标

为提升列车过岔的行车舒适性，保持道岔结构和列车运行的稳定性，并控制构件磨损速率，延长道岔使用寿命，需在准静态条件下，控制高速道岔平面线型评价参数，宽轨距25号单开道岔平面线型评价参数，如表2所示。各方案均满足规范限值要求[2-3]，动能损失仅与行车速度和冲击角有关，中国规定高速道岔设计时，其值不大于0.65 km2/h2，经计算可得冲击角容许值0°23′5.81″，方案一始转辙角最小，列车侧逆向进岔的冲击角和轮轨撞击动能损失最小，但辙叉侧股跟端处存在冲击角；方案三未被平衡离心加速度及其增量最小，但辙叉跟端固定和电务设置的空间较小，不利于传递心轨温度力和减小扳动力；方案四道岔全长较长，造价较高。

表2 宽轨距25号单开道岔平面线型评价参数

1.2 车辆-道岔耦合动力学响应对比

根据四种线型的设计方案，应用多体动力学软件SIMPACK建立车辆—道岔耦合动力学模型，在不同线型方案下，计算列车以检算速度130 km/h通过莫喀高铁25号交叉渡线道岔的轮轨动态相互作用、列车运行安全性、平稳性和磨耗功率评价指标。

相比于方案三，方案四仅将道岔后长延长了3.047 m，主要是解决可动心轨辙叉电务系统及跟端固定问题。由于线间距均为5 m的情况下，列车通过线型方案三与线型方案四的动力响应相同，故以下图中只列举线型方案一～方案三的计算结果。

1.2.1 轮轨动态相互作用

轮轨力峰值对比结果，如图1、图2及表3所示。由对比结果可知，对不同线型，轮轨垂向力在列车通过夹直线并冲击第二道岔辙叉时出现峰值，不同线型下轮轨垂向力峰值差别较小。方案一轮轨垂向力最大值最小，方案三(四)轮轨垂向力最大值最大。

图1 轮轨垂向力

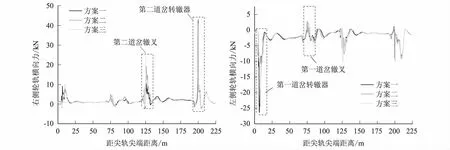
图2 轮轨横向力

计算位置第一道岔转辙器第一道岔辙叉第二道岔辙叉第二道岔转辙器线型方案方案一方案二方案三方案一方案二方案三方案一方案二方案三方案一方案二方案三轮轨垂向力/kN85.00 85.64 84.38 97.85 98.23 97.25 107.90111.44113.1990.1089.8890.34轮轨横向力/kN26.30 24.15 18.98 4.96 4.60 4.9910.5019.4028.7542.1043.3940.94

列车侧逆向进入第一道岔转辙器时，方案一在尖轨尖端所接线型为圆曲线，故轮轨横向力较大；同理，方案三(四)在导曲线起点处导曲线半径较大，故轮轨横向力最小。当列车通过夹直线进入第二道岔辙叉部分时，方案三(四)比方案二的夹直线长度短，故列车过岔的轮轨横向力响应较大；方案一夹直线与第二辙叉跟端连接位置的圆曲线半径最大，列车过岔的轮轨横向力最小。列车通过第二道岔后，轮缘在尖轨尖端附近与钢轨发生碰撞，引起较大的轮轨横向力，不同线型下轮轨横向力幅值差别较小。

1.2.2 列车运行安全性

列车运行安全性评价指标，如图3、图4及表4所示。由评价指标可知，脱轨系数分布规律与轮轨横向力相似。当列车侧逆向进入第一个道岔时，方案一线型下脱轨系数最大，方案三(四)线型下脱轨系数最小。当列车通过夹直线进入第二道岔辙叉时，综合考虑夹直线长度和第二辙叉跟端圆曲线半径的影响，方案一线型下脱轨系数最小，方案三(四)线型下脱轨系数最大。当列车离开交叉渡线，并冲击第二道岔尖轨前端时，脱轨系数迅速增大，方案二线型下脱轨系数最大。各方案中，轮重减载率的最大值相近。

图3 脱轨系数

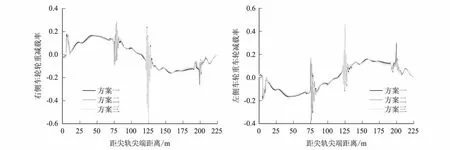
图4 轮重减载率

计算位置第一道岔转辙器第一道岔辙叉第二道岔辙叉第二道岔转辙器线型方案方案一方案二方案三方案一方案二方案三方案一方案二方案三方案一方案二方案三脱轨系数0.320.290.240.070.060.070.140.230.260.550.580.50轮重减载率0.180.180.160.270.280.270.420.450.470.300.320.32

3种方案下脱轨系数最大值为0.58，轮重减载率最大值为0.47，均满足TB/T 3301-2013《高速铁路道岔技术条件》脱轨系数≤0.8、轮重减载率≤0.65的要求。

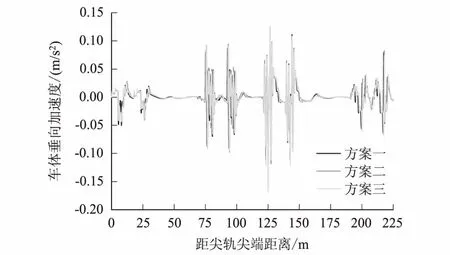
图5 车体垂向加速度

1.2.3 列车运行平稳性

车体振动加速度最大值如图5、图6及表5所示。由加速度最大值可知，不同线型下车体振动加速度差别较小。3种方案下，车体垂向加速度最大值为0.17 m/s2，横向加速度最大值为0.76 m/s2，分别满足TB/T 3301-2013《高速铁路道岔技术条件》车体垂向加速度≤2.0 m/s2、车体横向加速度≤1.5 m/s2的要求。由此可知，此平面线型舒适度较高。

图6 车体垂向加速度

线型方案方案一方案二方案三垂向加速度/(m/s2)0.150.160.17横向加速度/(m/s2)0.760.700.74

1.2.4 磨耗功率

车体磨耗功率如图7及表6所示。列车侧逆向进岔时，方案一由于尖轨前端工作边为圆曲线，故列车进岔时，车轮与位置更靠前、顶宽更小且结构更薄弱的曲尖轨界面发生碰撞，轮缘接触引起较大的磨耗功率。方案一在第一道岔转辙器位置的磨耗功率最大。列车侧顺向通过第二道岔出岔时，右侧轮缘冲击曲尖轨，并出现磨耗功率峰值。在方案二线型下，轮缘冲击曲尖轨前端使其磨耗功率最大。列车通过辙叉时磨耗功较小，侧股可动心轨辙叉可不设置护轨。

应用列车-道岔空间耦合动力分析仿真系统分析了列车通过单开渡线道岔时，夹直线长度对行车安全性和舒适性的影响，最终选用平面线型方案一。

图7 磨耗功率

计算位置第一道岔转辙器第一道岔辙叉第二道岔辙叉第二道岔转辙器线型方案方案一方案二方案三方案一方案二方案三方案一方案二方案三方案一方案二方案三磨耗功率/(Nm/s)4 8104 7174 7351 4321 3621 5505 1345 5845 2669 1459 3387 987

2 道岔轮轨关系设计

为提高列车通过道岔的平稳性，提出了基于接触迹线外移的低等效锥度直基本轨轨顶廓形设计方案；为减缓高速列车通过道岔时轮轨动态相互作用，提升行车安全性，形成了翼轨垂向抬高结构设计方案；为实现高速道岔低动力设计，开展了道岔刚度均匀化设计。

2.1 基本轨结构优化设计

列车直逆向通过道岔且轮载过渡至直尖轨前，由曲基本轨弯折引起的固有结构不平顺使尖轨侧轮轨接触点外移，增大轮对滚动圆半径差，加剧列车横向动力响应。为提升列车过岔平稳性，德国BWG公司基于动态轨距优化设计方案(FAKOP)加宽尖轨轨距，使轮对通过转辙器时两侧车轮的滚动半径趋于相同，减缓了蛇形运动；CATFERSAN方案通过切削直基本轨轨距角，控制滚动圆半径差[4]。

本文通过优化轮载过渡起始位置直基本轨轨顶廓形，使轮载过渡前两侧轮轨接触点同步外移，从而减小滚动圆半径差。考虑长期服役状态下道岔轮轨关系的演变，拟定列车直逆向通过道岔的横移量范围为±8 mm，基于迹线法[5]可知，在顶宽15 mm直尖轨断面(l1=2.492 m)，轮载开始从曲基本轨过渡至直尖轨。设控制截面轨顶廓形的离散坐标为(hi,vi) (i=1, 2, …,n)，其中，hi和vi分别为优化廓形控制离散点的横向和垂向坐标，横坐标hi可视为常数，轨顶廓形可表示为f(vi)。则在指定的轮对横移量yk下，轮对滚动圆半径差Δrk可表示为：

Δrk=Δrk(yk,v1,v2,…,vn)

(1)

假设轮对横移量yk在±12 mm范围内满足正态分布(μ,σ2)，其中，数学期望μ为0，标准差σ2为4，考虑不同轮对横移量yk的权重系数wk，平均滚动圆半径差S可表示为：

(2)

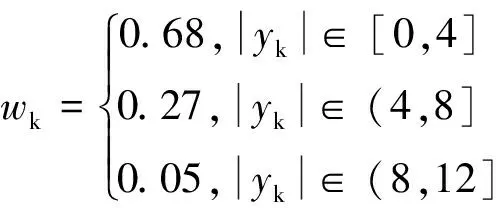
(3)

式中：m——轮对横移量的总计算次数。

由于轮对横移量yk已知，式(2)可改写为以下形式，并作为截面B-B优化轨顶廓形的目标函数：

S=S(v1,v2,…,vn)

(4)

钢轨廓形为严格凸曲线，在优化过程中，为保证钢轨廓形的真实性，定义了约束函数：

(5)

结合钢轨廓形的初始状态和优化能力，变量vi的边界范围可定义为：

ai≤vi≤bi,i=1,2,…,n

(6)

采用结合Quasi-Newton和BFGS方法的二次序列优化法(SQP)[6]对直基本轨C-C断面进行优化。根据式(4)～式(6)，该优化问题可表达为：

min：S=S(v1,v2,…,vn)

st:Gi>0；ai≤vi≤bi,i=1,2,…,n-1,n

(7)

结合莫喀高铁列车的CR15车轮踏面廓形，计算所得控制截面的优化轨顶廓形。假设顶宽71 mm直尖轨(l2=7.869 m)对应里程，通过线性插值得到纵向连续变化的直基本轨廓形，基于迹线法所得转辙器范围内滚动圆半径差变化，如图8所示。可知上述优化方案显著减小了轮载过渡前的轮对滚动圆半径差，但随着尖轨侧轮轨主接触点过渡至内侧尖轨，直基本轨侧接触点外移使滚动圆半径差增大，不利于轮载过渡后的行车平稳性。故提出通过缩小控制截面与截止截面之间的距离l2，降低基本轨侧接触点变化对行车平稳性的影响。

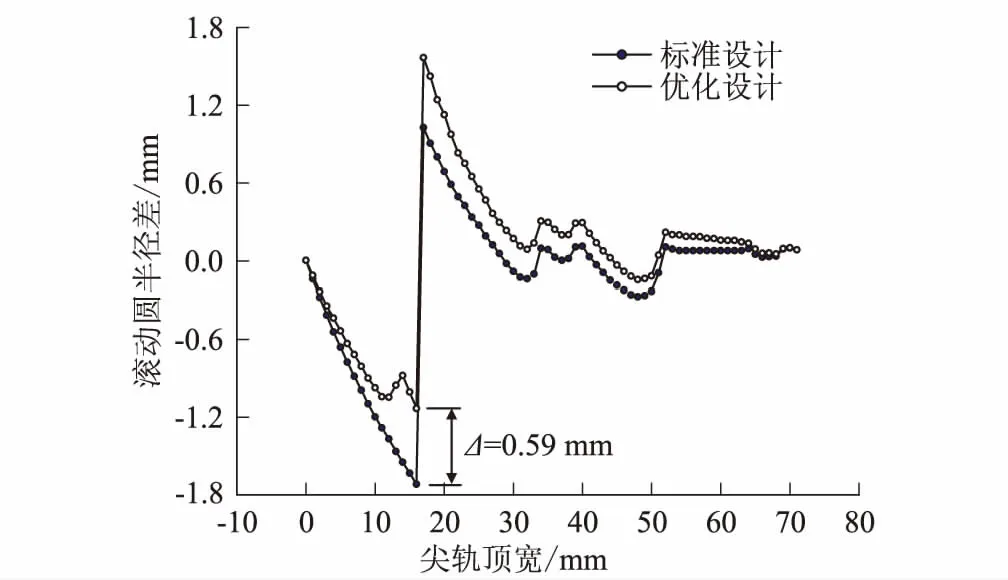
图8 优化前后滚动圆半径差对比图

当分别考虑l2为7.869 m、 2.0 m、1.0 m和0.5 m时，应用多体动力学软件建立高速车辆-道岔系统动力学模型[7]，对比车辆直逆向过岔的系统动力响应变化，如图9所示。优化截止截面设计显著降低了轮载过渡时车体横向振动加速度，由接触迹线外移所加剧的系统横向动力响应随l2减小而减缓；当l2为1.0 m时，相比于标准设计工况，轮对横移量和车体横向振动加速度分别降低了56.2%和50%，直基本轨顶面加工廓形设计显著提高了行车平稳性。

图9 车辆-道岔系统动力响应图

2.2 翼轨结构优化设计

可动心轨辙叉垂向结构不平顺较大，列车以时速400 km直逆向通过道岔时，由轮载过渡引起的轮轨动态相互作用剧烈，轮重减载率接近限值。辙叉轮轨关系设计应减小垂向结构不平顺，因心轨水平藏尖设计受结构限制，对垂向不平顺的减缓作用较为有限。为此，通过翼轨垂向抬高，抵消因心轨降低引起的垂向不平顺，以减缓辙叉部分轮轨动态相互作用，延后轮载过渡位置至心轨粗壮断面。

基于车轮踏面与翼轨或心轨轨顶的接触斑椭圆长轴为10 mm的原则，设计翼轨轨顶廓形。为简化设计，直股与侧股翼轨抬高取值相同，考虑顶宽20～50 mm长心轨为轮载过渡范围，提出了在心轨实际尖端至顶宽50 mm心轨范围内抬高翼轨、顶宽30 mm心轨处翼轨抬高量为最大值2.2 mm的翼轨垂向抬高方案。翼轨抬高前后系统动力响应对比，如图10所示。从图中可以看出，车轮抬升量定义为车轮名义滚动圆与接触踏面的交点相对于基本轨轨顶平面的垂向运动量，反映车辆过岔动态作用下，道岔垂向结构不平顺。翼轨抬高显著减小了垂向结构不平顺，使车辆直逆向和侧逆向过岔时长心轨范围内轮轨垂向力最大值分别降低14.60 kN和16.85 kN。翼轨抬高前后等效锥度对比，如图11所示，从图中可以看出，翼轨抬高延后了轮载过渡至长心轨的位置，有利于减缓心轨前端薄弱断面的磨耗和滚动接触疲劳伤损，延长道岔心轨使用寿命；轮载过渡后等效锥度最大值减小了34.54%，提升了行车平稳性。

2.3 道岔刚度均匀化

建立道岔瞬态有限元模型[8]，分析了道岔轨道整体刚度沿线路纵向分布规律。道岔轨下基础刚度主要由扣件系统和道岔板提供。无砟道岔刚度很大，若改变其刚度需在道床板下设置橡胶垫层，造价高且损坏后难修复；扣件系统的轨下胶垫需保证可动轨件与基本轨、翼轨的动态高差，刚度较大，难以调整其刚度。铁垫板下的橡胶垫板是扣件系统弹性的主要来源，改变其刚度可改变轨道刚度，可通过合理设置板下胶垫的刚度实现岔区轨道刚度的均匀变化。通过改变沟槽、分块、分层等方式可实现，但为了道岔轨道刚度的统一，不宜通过改变板下垫层厚度来实现，同时为了铺设和更换方便，共用垫板下胶垫的刚度宜分级设置，并且尽可能少设。

图10 翼轨抬高前后系统动力响应对比图

图11 翼轨抬高前后等效锥度对比图

道岔刚度均匀化的优化区域划分，如图12所示。其中Ⅰ区为普通板下胶垫，刚度最大；转辙器范围内尖轨与基本轨共用滑床板，考虑沿纵向变化的变截面尖轨刚度，转辙器划分为Ⅱ和Ⅲ两个区域；导曲线中两导轨共用铁垫板的范围划分为区域Ⅳ；将辙叉趾端两根翼轨和辙叉跟端两根心轨共用垫板的范围划分为区域Ⅴ；在辙叉咽喉以后，两根翼轨、长心轨和短心轨共用垫板，在间隔铁的强约束作用下，钢轨抗弯刚度较大，故该区域Ⅵ的板下胶垫刚度值最小。

岔区轨道刚度均匀化目标值为80±5 kN/mm/m，钢轨挠曲变化率应该满足0.3 mm/m的要求，里基刚度比有所下降，道岔刚度均匀化降低了轨道刚度变化引起的动态不平顺，减小了轨道结构振动强度。

3 道岔无缝化设计

莫喀高铁道岔地处高纬度严寒地区，年轨温变化范围大，无缝道岔钢轨易变形，较大的尖轨伸缩量可引起转换卡阻，破坏道岔结构稳定性。通过研发适应大伸缩量的新型钩型可靠锁闭机构，调整尖轨跟端限位器子母块间隙，创新尖轨跟端传力结构，开展道岔无缝化设计。

3.1 新型钩型锁闭机构

传统的尖轨外锁闭装置，如图13所示。尖轨连接铁与锁闭钩通过螺栓相连，为适应牵引点处尖轨伸缩，锁闭钩可在销轴一定长度范围内纵向平动。新型钩型锁闭机构，如图14所示。尖轨连接铁通过双层滑块与锁闭钩相连，锁闭钩可绕双层滑块转动，以适应可动轨件伸缩，满足莫喀高铁道岔钢轨高温差伸缩变形的需求。

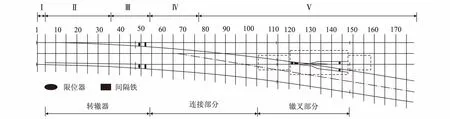
图12 道岔刚度均匀化分区图

图13 传统尖轨外锁闭装置示意图

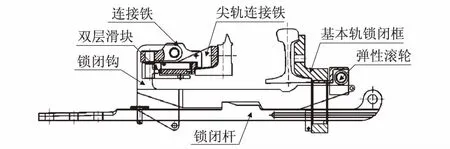
图14 新型钩型锁闭机构示意图

3.2 尖轨跟端传力结构

莫喀道岔尖轨跟端布置了两组限位器，通过建立路基上无砟结构无缝道岔计算模型[9]，分析了无缝道岔纵向力传递机理及横向胀轨规律，如图15所示。传统设计中，不同位置限位器子母块间隙均相等，在当地年轨温差62.5℃下，通过调整限位器子母块间隙值可知，相比于靠近尖轨跟端的限位器，靠近尖轨尖端的限位器所受的集中纵向力增大约100 kN，两组限位器所对应的尖轨与基本轨相对位移差约为1.65 mm。限位器受力不均易破坏道岔的几何状态，在纵向力集中处引起碎弯。因此，本文提出了将两组限位器子母块间隙差值调整为2 mm。在2 mm限位器间隙差下，不同限位器间隙组合的无缝道岔钢轨受力与变形情况，如图16所示。通过调整限位器子母块间隙，两组限位器传递的纵向力差值显著减小，能最大限度满足同步受力的要求。综合考虑限位器均匀受力、减小限位器所受纵向力和控制尖轨尖端伸缩位移的要求，限位器子母块间隙采用12 mm和10 mm的组合。

图15 考虑限位器7 mm间隙下25号道岔中各钢轨的温度力和位移分布图

图16 无缝道岔钢轨受力与变形图

4 道岔转换设计

运用有限元法建立了莫喀高铁25号道岔转换有限元计算模型[10]，对转换牵引点间距及其动程进行优化设计，形成了25号道岔尖轨设置5个牵引点，心轨设置3个牵引点，采用多机多点，牵引点间布置密贴检查器的牵引方案。为控制长大轨件的转换不足位移，预防可动轨件扳动力过大，提出采用减磨滚轮滑床台板方案，以降低摩擦阻力；通过铣削长心轨工作边轨肢和短心轨非工作边轨肢，减少长短心轨可动段的间隔铁数量，将心轨第三牵引点后的间隔铁替换为顶铁等措施，降低可动轨件的横向刚度。

道岔采用新型钩型锁闭机构，能有效克服尖轨在密贴时的转换阻力，并锁闭道岔轨件。以尖轨第三牵引点为例，当道岔转换牵引点存在异物，在不同尖轨转换力下，新型钩型锁闭机构完成锁闭所需要的锁闭杆支反力小于传统外锁结构，该锁闭结构设计更安全可靠。两种锁闭机构的锁闭杆支反力对比，如图17所示。

5 结论

本文综合考虑莫喀高铁速度高、宽轨距、高寒环境、客货共线运营等特点，形成了莫喀高铁25号道岔平面线型、轮轨关系、无缝化和转换设计等设计关键技术，满足行车安全舒适性、道岔低动力设计、 高平顺性和转换锁闭可靠性的要求。得出以下几点主要结论：

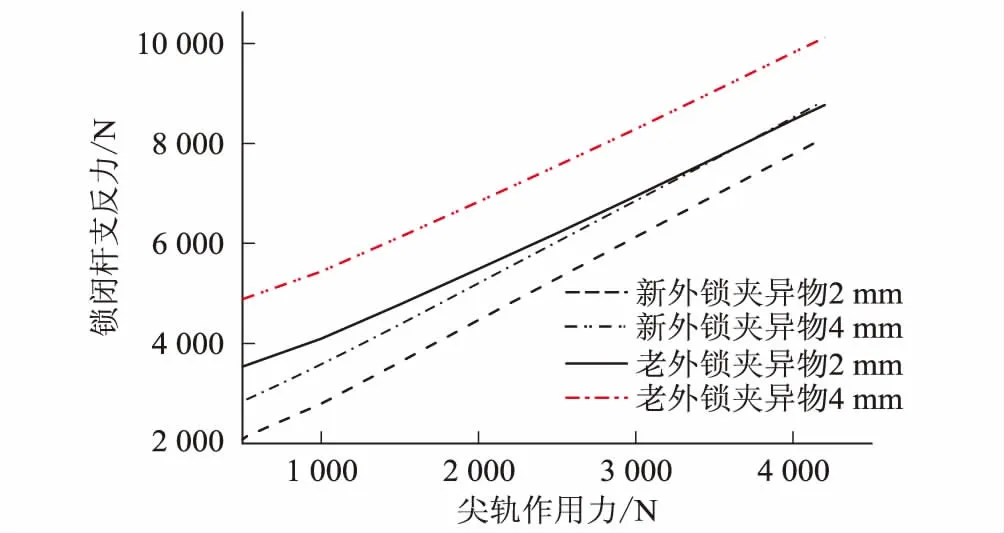
图17 两种锁闭机构的锁闭杆支反力对比图

(1)提出了侧股圆曲线半径为2 800 mm+2 230 mm的圆缓圆25号道岔平面线型方案，其始转辙角较小，轨距线交点距辙叉跟端距离较长，能满足行车舒适性、减缓构件磨耗速率、电务设置和经济性等要求。

(2)基于接触迹线外移的新型轮轨关系设计理念，提出了直基本轨顶面加工廓形方案，显著提高了行车平稳性，转辙器范围内轮对横移量和车体横向振动加速度分别降低了56.2%和50%。为减小辙叉垂向结构不平顺，开展了翼轨垂向抬高结构设计，车辆直逆向和侧逆向过岔时长心轨处轮轨垂向力最大值分别降低了14.60 kN和16.85 kN；轮载过渡位置后移减缓了心轨磨耗等伤损。考虑道岔钢轨间支撑和约束条件差异，提出了弹性均匀的岔区轨道刚度技术。

(3)研制了通过锁闭钩转动，适应可动轨件大伸缩量的新型钩型锁闭机构，并通过调整转辙器跟端两组限位器的子母块间隙，使其满足同步受力要求，保证了无缝道岔的高平顺性。

(4)确定了25号道岔尖轨设置5个牵引点、心轨设置3个牵引点、采用多机多点、牵引点间布置密贴检查器的牵引方案，通过降低摩擦阻力和可动轨件横向刚度，形成控制长大可动轨件转换不足位移、减小扳动力的方案。应用新型钩型锁闭机构能提高高速道岔的锁闭可靠性。