尾矿库洪水漫顶溃坝实验研究及数据分析

李 钢，张 红，杨 曌

(1.中国安全生产科学研究院，北京 100012；2.中国安全生产科学研究院国家安全监管总局矿山采空区灾害防治重点实验室，北京 100012；3.华北科技学院，河北 三河 065201)

截至2015年底，我国共有尾矿库8 869座，其中五等尾矿库占总量的64%，停用尾矿库数量占总量的33%。自2001～2015年间我国共计发生溃坝事故38起，其中洪水漫顶引发的溃坝事故占事故总量的37%，是尾矿库事故的主要原因之一[1]。在加强尾矿库日常安全监管，降低事故隐患的基础上，研究洪水漫顶溃坝的演化过程、下泄流量及冲击距离，对遏制尾矿库事故，降低事故后果严重程度具有重要意义。

在尾矿坝溃坝演化过程及演化机理方面，诸多学者对其进行了研究。HASSAN等[2]研究了筑坝材料和尾矿库库容、库区上下游水位差等对坝体失稳过程的影响；HANSON等[3]研究了黏土坝的漫顶溃坝过程，并将溃坝过程分为4个阶段；敬小非等[4]开展了洪水水位条件下尾矿坝滑塌失稳模型试验，重点研究了由坝体浸润线过高引发的滑坡溃坝模式；郑欣等[5]开展了尾矿坝渗透破坏溃坝模型试验，发现尾矿料沉积分层对坝内浸润线的位置和形状影响较大；秦柯等[6]采用概化模型，以尾砂干燥、湿润状态和溃口形态作为变量进行冲刷试验，对溃口发展形态及速度进行了研究；张力霆等[7]进行了坝体排渗系统失效致使浸润线持续升高而诱发的尾矿库溃坝模型试验，利用坝体位移跟踪测量系统对尾矿库坝体溃决的演进过程进行了观测，总结了试验过程中的溃决模式。王永强等[8]以四川尾矿库为研究背景，以倾斜挡板代替模型坝模拟堆积坝坡，通过溃坝试验研究了尾矿料与水混合物在下游沟谷的演进流动特性。目前国内外在尾矿坝物理模型研究方面普遍缺乏对尾砂下泄流量、过泥深度、冲击距离等内容的研究。

本文基于相似理论建立了尾矿库洪水漫顶溃坝物理模型，在研究坝体漫顶溃坝过程中泥沙演进规律的基础上，进一步研究了尾砂的冲击速度、下泄流体过泥深度、冲击距离等内容，并将实验结果与尾矿库溃坝计算模型结果进行对比，验证了本次溃坝物理模型实验数据的适用性、准确性，实验结果可为洪水期尾矿库的安全管理尤其是库区下游的管理工作提供理论和技术支撑。

1 相似理论

1.1 相似第一定理

若两物理体系相似，则二者必可由同一方程式描述，各变量之间存在一定比例关系(相似常数)。该定理是相似的必要条件。由于相似现象均属于同一类现象，因此，它们具有相同的方程组；用来表征这些现象的一切量，在空间中相对应的各点及在时间上相对应的各瞬间，各自互成一定的比例关系；相似现象必然发生在几何相似的对象里；由于相似对象的一切量各自互成比例，而由这些量所组成的方程组相同，因此可知各量的比值彼此约束。

原形采用方程式(1)描述；模型采用方程式(2)描述；若存在式(3)中的相似比例系数，则式(1)可描述为式(4)；式(4)分解后可表达为式(5)；式(6)与式(5)等价，即原形与模型各相似常数之间应满足的关系式。

f(x1,x2,……xn)=0(1)

f(y1,y2,……yn)=0(2)

xi=aiyi(3)

f(a1y1,a2y2,……anyn)=0(4)

G(a1,a2,……an)·f(y1,y2,……yn)=0(5)

G(a1,a2,……an)=1(6)

1.2 相似第二定理(模拟定理)

令λi为原形与模型的xi变量中的同一数值比，由相似准则可知，λi(i=1,2,……n)之间存在着某种关系，这种关系叫做模拟定理，或者相似条件，λi称为比例因数。

对于长度量纲和应力量纲的变量，均具有相同的比例因数，见式(7)～(8)。

λL=λH=……(7)

λE=λC=λG=……(8)

式中：λL为长度比例因数；λH为高度比例因数；λE为弹性模量比例因数；λC为内聚力比例因数;λG为自重比例因数。

对于无量纲变量，同样具有相同的比例因数，且该比例因数等于1，见式(9)。

1=λμ=λφ=……(9)

式中：λμ为泊松比比例因数；λφ为内摩擦角比例因数。

1.3 相似第三定理(π定理)

众多物理、力学现象，均可用数学方法表示成函数形式，见式(10)。

f(x1,x2,……xn)=0(10)

xi(i=1,2,……n)是描述和影响该现象的变量，n为变量总个数。根据相似原理可写成无量纲形式，见式(11)。

F(π1,π2,……πn)=0(11)

式(11)中πl(l=1,2,……m)是原始变量xi的无量纲乘积组合量，称为无量纲变量。其中π项读数m与原始变量总数n同包含在原始变量xi(i=1,2,……n)中的基本量纲数γ之间存在着如式(12)所示关系。

m=n-γ(12)

若变量xi(i=1,2,……n)彼此之间是相互独立的，则πl(l=1,2,……m)之间也是相互独立的，且完全可以用函数F(πl)来代替f(xi)来描述研究对象。

2 漫顶溃坝实验

2.1 研究目的

尾矿库洪水漫顶溃坝物理模型实验主要研究内容：溃坝过程中溃口的演化规律；尾砂的下泄流量及冲击距离。

2.2 溃坝模型

以我国南方某山谷型尾矿库为例，该尾矿库东、南、北三面环山，为一葫芦状谷地。西部为出口，标高在145～350 m之间。谷地东高西低，谷地坡度约为2%。

尾矿坝坝体为均质土坝，采用水力旋流器分级尾矿按中线法堆积而成，坝高35 m，库区长度60 m，外坡比1∶2.0，内坡比1∶1.8，干滩面长度30 m。根据模型相似理论，尾矿库原型与试验模型主要物理量间的关系见表1。

表1 原型与实验模型主要物理量间的关系Table 1 The relationship between the prototype and the physical quantity of the experimental model

漫顶溃坝试验模型按照1∶100比例尺缩小，尺寸为60 cm×35 cm×30 cm(长×高×宽)，外坡比1∶2.0，内坡比1∶1.8。

2.3 溃坝实验装置

漫顶溃坝装置平台由模型区、冲刷区、注水系统、监测系统等构成。模型区为1.5 m×1 m×3 m(长×宽×高)的立体空间，模型底部铺设防渗垫；冲刷区为4 m×2 m×3 m立体区域，为防止尾砂下泄阶段遇障碍影响溃决效果，模型冲刷区内设置4 m×2 m(长×宽)的下泄区域，下泄区域地面平坦、干燥，可为溃坝后尾砂下泄提供充足的空间，并可用于研究尾砂溃坝过程中的运动轨迹规律及溃坝结束后坝底的过泥深度；注水系统用于模型注水，待达到设计要求水位及流量后通过调节注水量保持库水位高度。

2.4 溃坝尾砂材料

实验尾砂取自库区内堆存的尾砂，尾砂实验参数通过常规三轴实验及尾矿库评估报告中岩土参数共同确定。尾砂详细物理参数见表2。

表2 尾砂物理参数表Table 2 Tailings physical parameters

模型各层尾砂布置依据库区内各层尾砂厚度以1∶100比例进行布置，土层1、土层2岩土参数一致，实验模型中均取库区土层1尾砂搭建，土层3取库区内该层尾砂搭建。结合库区内三层尾砂的厚度，土层3位于模型底端，厚度15.36 cm，其余均为土层1尾砂。

2.5 监测设备布置

实验设备主要包含：尾矿砂、秒表、高画质相机、测量工具(直尺)、尾矿库模具等。

设备布置：①在坝底的坝基底部、距坝基20 cm、40 cm、70 cm、100 cm五个位置分别布置过泥深度测量点JC1-JC5，在坝体薄弱易溃坝位置布置流速监测点LS1-LS7，在水位变化稳定位置布置水位监测点SW1-SW3，监测坝体溃坝过程中水位变化过程及溃坝稳定后坝体下游的过泥深度；②在坝体3 m处布置高像素相机，拍摄坝体溃坝全过程；③在坝体上方设置秒表，自溃坝开始时计时，至溃坝终止后停止计时。尾矿坝监测点布置如图1所示。

在整篇小说中，“我”不管同父亲还是母亲都自始至终进行着看起来完全不在一个维度上的无效对话，“我不能把我要讲的事讲清，哪怕一点点”[3]，所有的对话和沟通似乎也被文中反复出现的大雾所遮蔽，变为一团“更浓的雾”。

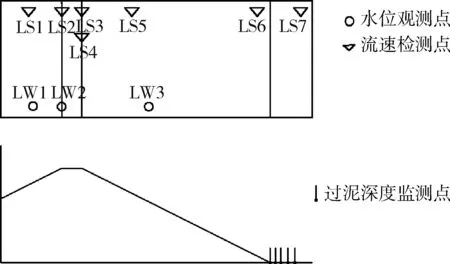
图1 尾矿坝监测点布置图Fig.1 Tailings dam monitoring points layout

3 溃坝实验结果及分析

溃坝模型构建完成后，在模型外坝坡上采用10 cm×10 cm的有限元网格，用于跟踪溃口演化规律。自注水系统向尾矿库库区内注水时起开始计时，至初次注水高度达25 cm(接近项目库区水位线)，停止注水，待充分浸润坝体后，再次注水至高度25 cm后停止注水，循环注水直至水位面不再变化，在该水位面的基础上再次注水(模拟洪水汇入)直至坝体发生漫顶破坏。

3.1 溃坝过程及其演化规律

注水40 min后坝体右侧边缘部位出现溃口，下泄水流自溃口处流出，坝体溃口部位及周边尾砂受水流冲蚀，形成泥石流向坝基流下。溃坝3 s后溃口宽5 cm，水流携带尾砂冲刷至坝底20 cm过泥深度监测点JC2。随着水流冲刷速度的加快，溃坝4 s后尾砂冲刷至40 cm过泥深度监测点JC3。水流冲刷过程中，溃口周边尾砂在水流及重力作用下出现滑移失稳，溃口左侧10 cm处出现3 mm裂隙，并沿坝体向下延伸发展。10 s后，下泄水流持续冲刷使得10 cm裂隙处坝体出现坍塌，溃口进一步扩展，24 s后尾矿坝重新达到平衡状态，最终坝体冲刷距离为148 cm，溃口为11.9 cm。

根据坝体溃口的发展过程可知：在洪水作用下，坝体受水流浸润侵蚀作用，薄弱位置首先出现溃口；随后溃口及周边泥砂与冲刷水流浸润结合形成泥石流沿坝坡冲刷下泄；坝坡表层尾砂在冲刷水流的作用下，不断与之相结合，在坝坡表面形成冲刷路径并沿路径下泄至坝基；随着溃口处水流的持续下泄，溃口及坝坡下泄路径周边泥沙在下泄水流的冲刷及自身重力的作用下，逐渐出现纵向的细微裂缝；随着水流的持续冲刷，裂缝进一步扩展并逐渐形成纵向贯通性裂缝，进而造成溃口周边坝体失稳坍塌；坝坡下泄路径周边泥砂随着下泄泥石流的运动一并被带至坝基，并在水流的冲击作用下，向下泄区域外围发展，直至库区内洪水被完全释放。

3.2 溃坝流量分析

在库区内布置水位尺，自溃坝开始每1 s读取一次库区水位线数据，至溃坝结束时止，统计库区内水位变化数据，通过对库水位下降曲线求导得到溃口流量过程曲线，见图2。

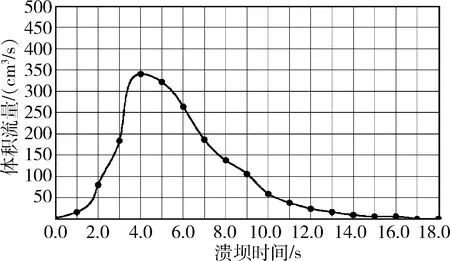
图2 溃口流量过程曲线图Fig.2 Tailings burst flow process curve

如图2所示，尾矿库溃坝开始阶段水流的流速较低，下泄尾砂流量较小，主要原因在于溃坝开始时水流流速低，水流对溃口的冲刷侵蚀速率较慢，溃口发展缓慢；随着水流的持续冲刷，溃口周边尾砂在水流及重力的双重作用下出现滑移失稳，造成溃口增加，而溃口的扩大又会导致溃口流速加快，出现下泄尾砂流量骤增，从而形成一个恶性循环，直至库区水位线下降至最低点，溃口水流逐渐减少，泥沙冲刷速度降低，冲刷流量同时持续降低直至溃口处边坡重回稳定状态。

3.3 溃坝泥深分析

溃坝过程结束后，采用毫米测量尺测量五处监测点的过泥深度，自坝基开始，过泥深度分别为：9.7 cm、8.1 cm、4.8 cm、2.1 cm、0.4 cm，尾矿砂至坝基外五个监测点的时间分别为：0.7 s、3.23 s、4.62 s、7.26 s、20.49 s。溃坝后冲击距离148 cm。根据过泥深度变化值可以看出所测泥深值随着测量距离的增加而降低。这说明溃坝后期下泄泥沙的携砂量逐渐减少，下泄泥沙的冲击力也相应减弱。在距离溃口100 cm(实际约为100 m)处，泥深均值已经降为0.4 cm(实际中约为0.4 m)。

3.4 溃坝模型估算值与测量值分析

本文选取在尾矿库溃坝模型研究中常用的溃坝计算模型，将实验测量到的数据与计算模型结果进行对比，验证试验模型数据的符合性。

3.4.1 尾矿库溃坝计算模型

1) 泄砂总量。在已有溃坝模型计算模拟中，泄砂总量的计算可根据尾砂的物理力学性质利用边坡稳定的分析方法进行估算。由于尾矿坝溃决时往往伴随着暴雨，库区尾矿呈饱和状态，所以一般在模型计算中考虑最不利情况，即泄砂总量取库段的全部库容。

2) 溃坝口平均宽度。据近50个库容在5.3万～55 000万m3、水头在46 m范围内的水库溃坝资料，统计得出溃坝口宽度的计算公式，见式(13)。

(13)

式中：b为溃坝口平均宽度；K为与坝体材料有关的系数，对黏土K值约为0.65，壤土K值约为1.3；W为溃坝时的泄砂总量；B为溃坝时坝前水面宽度；H为溃坝时水头。

3) 坝址最大砂流量。本文选取黄河水利委员会水利科学研究所根据实验求得的公式计算坝址最大砂流量，见式(14)。

(14)

式中：QM为溃坝时坝址最大砂流量；b为溃坝口宽度；B为尾矿库水面宽度；h为溃坝口残坝坝顶至水面的距离；H0为坝前水深；g为重力加速度。

4) 尾砂泄空时间。尾砂泄空时间表达式见式(15)。

(15)

式中，K为尾砂泄空时间系数，对于四次抛物线，K一般取4～5。

3.4.2 计算结果及分析

试验中的泄砂总量数值无法通过测量直接得到，因此采用简化三维溃口模型进行计算。通过测量溃坝过程完成后溃口的各项关键数据，然后简化溃口模型，采用简化的溃口三维模型计算出实际的溃坝泄砂总量，溃口各项尺寸测量数值见表3。

计算模型的泄砂总量采用了库区全部库容进行计算。试验模型及计算模型各项数据计算结果如表4所示。通过对比可知试验模型的溃口平均宽度、坝址最大砂流量和尾砂泄空时间都要小于模型计算值，考虑到模型估算是从最不利的情况进行考虑和分析，因此，通过尾矿坝常用的计算模型验证认为本次实验数据能够比较准确的描述溃坝过程，可用于尾矿库溃坝灾害评估等安全评价技术中。

表3 溃口尺寸数据表Table 3 Tailings burst size data

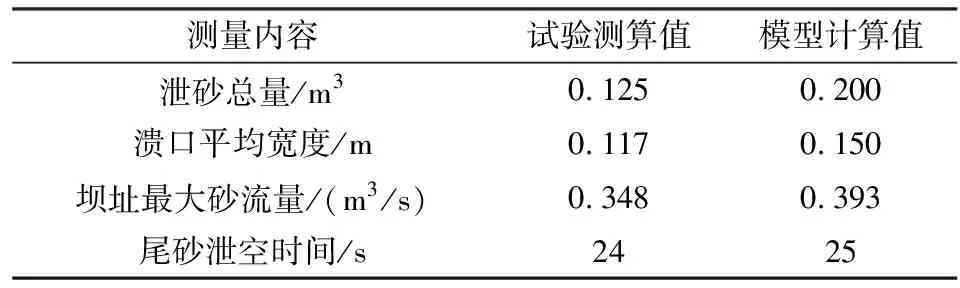
表4 试验模型与计算模型结果分析Table 4 Analysis of test model and calculation model

4 结 论

1) 基于相似理论建议尾矿库溃坝模型，按照1∶100比例尺构建试验模型，模型的尺寸为60 cm×35 cm×30 cm(长×高×宽)，外坡比1∶2.0，内坡比1∶1.8。

2) 通过模拟尾矿坝洪水漫顶溃坝实验，研究了坝体垮塌过程中溃口的发展规律、溃口流量以及下泄流体过泥深度和最终冲击距离。结果表明，坝体溃口的发展程度取决于漫顶水流侵蚀作用，下泄流量曲线受水流侵蚀及溃口扩展的双重影响，随着冲刷速度增高溃口扩大出现泄流量骤升，水流冲刷速度降低溃口稳定则下泄流量缓慢下降最终趋于稳定。

3) 将实验中泄砂总量、溃口平均宽度、最大泄砂量、尾砂卸空时间各项数据与模型计算结果对比分析可知，本次实验数据能够比较准确的反映漫顶溃坝过程。根据模型溃坝后冲击最远距离为148 cm可知，该尾矿库坝体漫顶溃坝冲击距离为148 m。