基于强度折减法的大型露天矿东端帮稳定性分析
2019-03-13康晓鹏韩廷文王金伟纪茜尧
康晓鹏,韩廷文,高 岩,王金伟,纪茜尧
(1.北京工业大学建筑工程学院,北京 100124;2.山东省第二地质矿产勘查院,山东 兖州 272100)
矿产资源露天开采的过程中,开挖边坡的稳定性研究是露天矿安全生产的关键技术问题,也是岩石力学等相关学科的基本命题。而随着矿产资源的开发利用,露天矿向深部开采建设中所遇到的岩质边坡稳定性问题也相应增多,特别是大型露天矿高边坡问题表现尤为突出[1]。近些年来,我国露天矿开采所占的矿石产量比重越来越大,国家对此的投入也越来越多,因此对露天矿开采矿高边坡的稳定性方面的研究也越来越深入。杨天鸿等[2]在收集整理国内外相关资料的基础上,通过对露天矿高陡边坡稳定性研究现状分析,提出了露天矿边坡岩体强度参数识别表征方法和动态稳定性评价方法;刘福明等[3]通过对露天矿排土场边坡降水入渗规律的研究,提出了提高露天矿排土边坡稳定性的建议。然而目前国内对露天矿高边坡稳定性与地下水位的关系分析大多数是建立在饱和岩土体的情况下,而对地下水位以上岩土体的饱和度变化很少考虑[4]。本文通过考虑地下水位以上的岩土体饱和度变化,结合夏日哈木镍钴矿区高陡边坡模拟计算出不同开采坡角的边坡稳定系数与地下水位的关系,确定出同一水位下的最小开采坡角,以及不同开采坡角下的最高地下水位。本次研究即对该地区类似工程具有重要的借鉴意义,也对以后高水位下露天矿的开采具有重要的工程使用价值。
1 露天矿开挖边坡研究区域概况
夏日哈木镍钴矿区地处青海省西部东昆仑山脉西段,镍钴资源量108万t,为大型镍钴硫化物矿床。拟规划建设年产矿石量561万t的露天采矿场,行政区划隶属于青海省格尔木市乌图美仁乡管辖。拟建的露天采场东西长1 670 m,采深一般在300 m以上,最高边坡高度超过600 m,为重要工程。露天采场设计生产服务年限约18年。
1.1 露天矿开挖边坡研究区域选择
根据边坡不同位置的边坡高度、工程地质岩组分布特征、各岩组岩石质量等级、边坡面倾向与各岩体的优势结构面的关系、露天采场边坡岩体完整程度等多项指标对边坡进行了分区,共分为5个区,分别为一区、二区、三区、四区和五区,各分区界线的方位角及主要工程地质岩组见图1。由于该大型露天镍钴矿东端帮即一区所占比重最大,故本文选取一区一号剖面线作为研究对象,其他区域可以以此区域为参考,运用同等方法依次研究。

图1 露天采场地质结构分区与剖面位置图Fig.1 Open-pit field geological structure zoning and profile map
1.2 露天矿开挖边坡研究区域地质特征
通过对此区域的工程地质勘查,该边坡主要分为坚硬-较坚硬块状辉长岩-辉石岩-花岗岩岩组和较坚硬-较软碎块状蚀变辉石岩岩组两个岩组。
坚硬-较坚硬块状辉长岩-辉石岩-花岗岩岩组,新鲜岩体呈块状结构,新鲜岩石致密坚硬,局部蚀变岩石较坚硬。由于辉长岩与辉石岩岩体各力学参数接近,现统一描述。该岩组块体平均密度2.86 g/cm3,岩石平均饱和单轴抗压强度62.45 MPa,软化系数0.92,内摩擦角29.6°,凝聚力5.6 MPa,平均吸水率0.11,平均弹性模量0.39×105MPa,平均泊松比0.18,平均渗透系数为3×10-6m/s。较坚硬-较软碎块状蚀变辉石岩岩组,岩体呈块状、碎块状结构。块体平均密度2.92 g/cm3,岩石平均饱和单轴抗压强度29.95 MPa,平均吸水率0.44%。根据工程地质孔资料,研究区域的主要岩体工程地质特征见表1。

表1 一区边坡主要岩体工程地质特征表Table 1 Geological feature of main rock mass engineering in area 1
2 计算参数的选择
2.1 边坡工程地质剖面分段
在各分区边坡上选择具有代表性的地段绘制边坡剖面图,并进行边坡工程地质岩组或岩体划分。在剖面图上及后文表格中用编号表示主要岩组或岩体,对应编号见表2。
再根据岩体完整程度、裂隙率、压水试验成果(透水率)、风化及蚀变程度等对研究区域1号剖面各岩组或岩体进一步分成各小区,用③-1、③-2等表示,见图2。

表2 各岩组或岩体对应编号表Table 2 Each rock group or rock masscorresponding number
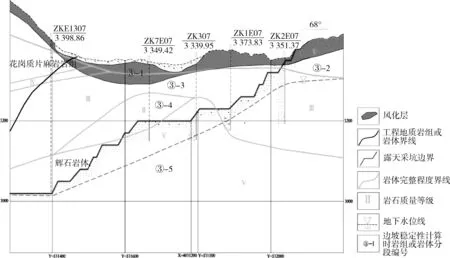
图2 1号剖面工程地质剖面图(一区)Fig.2 Section 1 engineering geological profile (Zone 1)
2.2 岩石强度指标折减计算
2.2.1 折减方法的选择
由于实验室做出的岩石强度指标不能直接应用于实际岩体,需进行折减计算。在岩体稳定性分析中,岩体抗剪强度指标是最重要的计算指标。根据岩块的抗剪强度,本文采用费辛柯法、M GEORGI法对岩体抗剪强度中的凝聚力进行弱化处理,然后求其平均值[5],见式(1)。
Cm=CI×I(1)
式中:Cm为岩体的凝聚力;CI为测试得到的岩石的凝聚力;I为折减系数。
1) 费辛柯法
费辛柯法是考虑岩体结构面间距和岩体破坏高度两个因素对岩块凝聚力进行弱化,其折减系数I由式(2)确定。
(2)
式中:a为岩石强度和岩体结构面分布的特征系数,参照不同分类岩石的a值,此处a取3.0[6];H为岩体破坏高度,根据各部边坡高度确定;L为破坏岩体被切割的原岩石尺寸,即结构面间距,根据各岩体节理裂隙密度确定。
2) M GEORGI法
M GEORGI对坚硬岩浆岩和变质岩岩块的岩体强度研究以后,得出式(3)所示经验关系。
I=0.114e-0.48(i-2)+0.02(3)
式中,i为节理裂隙密度指数,根据各岩体节理裂隙密度确定。
通过上述两种方法进行抗剪强度中的凝聚力折减后,取其算术平均值作为抗剪强度凝聚力值。摩擦角的折减目前还没有相关公式,一般按经验系数折减,参考同类工程取法,摩擦角的折减系数取0.85。
2.2.2 折减结果
本次研究对研究区内主要岩体进行了三轴压缩试验,共取岩样五组,其试验成果见表3。根据上述剖面图上划分的各岩体分段的裂隙密度不同,对各岩性段的岩石三轴压缩试验抗剪强度进行折减计算,折减后的抗剪强度见表4。
2.3 水位设置的参数选择
水位设置需考虑土的饱和度与基质吸力即孔隙压力的关系,以及渗透系数随孔隙压力的变化关系。透水性系数即渗透系数Kw也可以用基质吸力(ua-uω)的函数式表达,此处用1964年BROOKS和COREY得到的基质吸力与饱和度关系曲线表达式来确定,见式(4)~(5)。
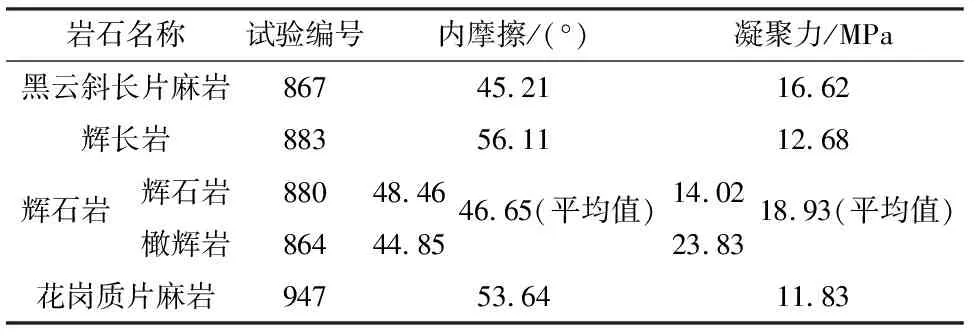
表3 三轴压缩试验成果表Table 3 The results of triaxial compression test

表4 1号剖面折减后岩体抗剪强度表Table 4 The shear strength of rock mass in section 1 after reduction
Kω=Ksfor (ua-uω)≤(ua-uω)b(4)

式中:Ks为饱和土(即S=100%)的透水性系数;Se为有效饱和度,此处剩余饱和度取为零,即有效饱和度即为饱和度;δ为经验常数。
不同土类的若干δ值及其相应的孔隙尺寸分布指标λ见表5。
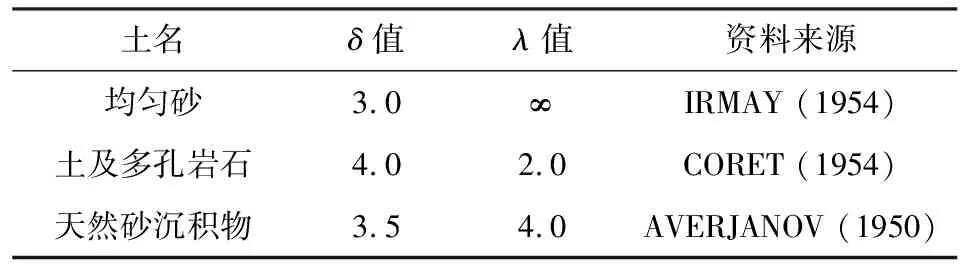
表5 不同土类常数δ的建议值及孔隙尺寸分布指标λ值Table 5 The suggested value of different soil type constantand the value of pore size distribution index
GARDNER建议的渗透系数与基质吸力的关系表达式见式(6)。
(6)
式(6)中提出一种由两个常数“a”及“n”所确定的适应性强的渗透性系数,常数n定义为函数的坡度,常数a相应于函数的断点,此处a取0.1,n取2[7]。
结合式(5)和式(6)得到土在非饱和状态下的渗透折减系数K_s的计算公式,见式(7)。
(7)
由此得到有效饱和度Se、渗透折减系数K_s随孔隙压力(ua-uω)的变化结果,见表6。
2.4 计算组合的选择
根据《非煤露天边坡工程技术规范》(GB/T 51016—2014),采用“自重+地下水”的组合对边坡稳定性进行分析。依据《非煤露天边坡工程技术规范》(GB/T 51016—2014),所研究的露天矿开挖边坡工程安全等级为Ⅰ级,由表7得出研究区域的最小设计安全系数Fst≥1.25~1.20(自重+地下水)[8-9]。这里未考虑地震作用、爆破震动等不利因素,根据相关工程经验,一般需要把计算出来的稳定系数进行折减,此处折减系数取0.90[10],即在自重加地下水作用下计算出来的最小安全系数要大于1.39~1.33,此处模拟计算出的最小安全系数取1.35。

表6 孔隙压力设置参数表Table 6 Pore pressure setting parameters

表7 不同荷载组合下总体边坡的设计安全系数Table 7 Design safety factors for general side slopesunder different load combinations
注:荷载组合Ⅰ为自重+地下水;荷载组合Ⅱ为自重+地下水+爆破振动力;荷载组合Ⅲ为自重+地下水+地震力。
3 东端帮边坡稳定性计算过程及结果分析
选取东端帮即一区的1号剖面线为研究对象,采用有限元软件ABAQUS,结合抗剪强度折减法分别计算开挖坡角为42°、44°、45°、46°及48°时在不同地下水位的稳定系数[11]。
3.1 ABAQUS中抗剪强度折减参数的计算
所谓抗剪强度折减技术就是将土体的抗剪强度指标C和φ,用一个折减系数FS,如式(8)和式(9)所示的形式进行折减,然后用折减后的虚拟抗剪强度指标CF和φF,取代原来的抗剪强度指标C和φ,见式(10)[12]。
CF=C/FS(8)
φF=tan-1((tanφ)/FS)(9)
τfF=CF+σtanφF(10)
式中:CF是折减后土体虚拟的黏聚力;φF是折减后土体虚拟的内摩擦角;τfF是折减后的抗剪强度。
折减系数Fs的初始值取的足够小,以保证开始时是一个近乎弹性的问题。然后不断增加Fs的值,折减后的抗剪强度指标逐步减小,直到某一个折减抗剪强度下整个土坡发生失稳,那么在发生整体失稳之前的那个折减系数值,即土体的实际抗剪强度指标与发生虚拟破坏时折减强度指标的比值,就是这个土坡的稳定系数。此处以边坡坡顶部位的位移拐点作为评价标准,经计算得到ABAQUS里所用的岩体折减参数,见表8。

表8 岩体参数折减结果表Table 8 Reduction of rock mass parameters
3.2 有限元软件ABAQUS数值模拟计算
本次研究使用有限元软件ABAQUS对开挖边坡稳定性进行的数值模拟分析,采用ABAQUS中的摩尔-库伦弹塑性模型,在研究过程中,首先利用Part模块建立开挖边坡模型,其中开挖坡角44°的数值模拟计算模型简图如图3所示,其余计算模型此处不再详细列出。之后通过Property模块选择材料模型并设置相关参数,定义各个截面属性,并将截面属性分配给相应区域实现材料分区。最后通过Assembly模块、Step模块、Load模块、Mesh模块及Job模块模拟计算得到一区1号剖面在42°、44°、45°、46°、48°坡角,且在不同水位下的安全系数。该研究以坡脚所处位置为±0.00 m,本次主要研究了200 m、230 m、260 m、290 m及330 m水位下的稳定系数,所研究边坡原水位线处于290 m,但考虑到下雨后地下水位变化,此处将330 m水位也加入研究。此研究未考虑地震力作用的影响,其中坡角45°时且水位线在260 m处该边坡的地下水位线及其水位以下孔隙水压力云图见图4;计算过程中其所研究边坡在坡角48°、水位230 m时的饱和度云图见图5;计算完成后会形成明显的潜在滑动面,其中坡角46°、水位260 m的潜在滑动面位置见图6;模拟计算出的相应稳定系数见图7。

图3 坡角44°时的计算简化模型图Fig.3 Calculate the simplified model when the slope angle is 44°

图4 坡角45°、水位260 m时的孔隙压力云图Fig.4 The pore pressure contours when the slope angle is 45° and water level is 260 m
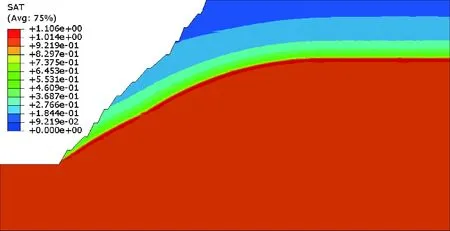
图5 坡角48°、水位230 m时的饱和度云图Fig.5 The saturation contours when the slope angle is 48° and water level is 230 m

图6 坡角46°、水位260 m时的潜在滑动面位置Fig.6 The potential sliding surface location when the slope angle is 46° and water level is 260 m
图7 坡角46°、水位260 m时的稳定系数Fig.7 The stability coefficient when the slope angle is 46° and water level is 230 m
3.3 计算结果分析
通过上述模拟计算,得到的东端帮即一区1号剖面在不同研究坡角角度,不同地下水位的稳定性分析见图8和图9。
由图8分析的一区边坡模拟计算结果可以看出:当地下水位为330 m时,所研究的露天矿东端帮的最小开挖坡角为43.5°;当地下水位为290 m时,所研究的露天矿东端帮的最小开挖坡角为45.3°;当地下水位为260 m时,所研究的露天矿东端帮的最小开挖坡角为46°;当地下水位为230 m时,所研究的露天矿东端帮的最小开挖坡角为47.5°。由此可见对于大型露天矿高陡边坡,地下水位的高度对开挖坡角角度产生了重要影响。
由图9分析的一区不同开挖坡角下稳定系数与地下水位的关系可以得出:当开挖坡角为42°及44°时,所研究的露天矿东端帮不需要降低地下水位;当开挖坡角分别为45°、46°、48°时,所研究的露天矿东端帮的最高地下水位分别为303 m、260 m、212 m。其中,在所研究的露天矿东端帮即一区边坡的五个不同开挖坡角中,各个坡角的挖方量差值见表9,表中的挖方量差值为单位宽度的挖方量。从表中得出增大开挖坡角角度对减小露天矿挖方量至关重要。
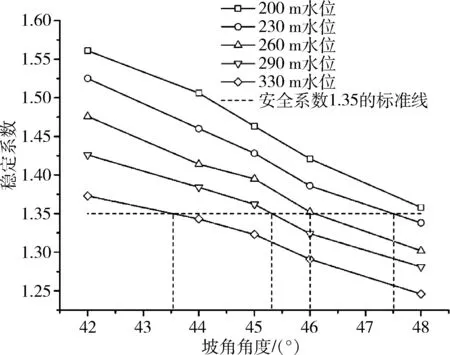
图8 不同水位下稳定系数随坡角角度变化图Fig.8 The stability coefficient at different water level changes with slope angle
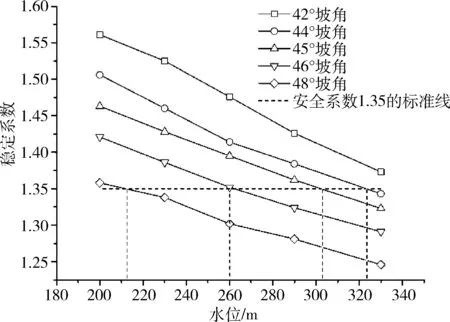
图9 不同开挖坡角下稳定系数随水位变化图Fig.9 The stability coefficient at different slope angle changes with the water level
表9 不同坡角挖方量差值表Table 9 The difference of the excavation volumeof different slope angles

V42°-V44°V44°-V45°V45°-V46°V46°-V48°挖方量差值/(m3/m)4 755.602 792.102 422.904 279.5
4 结 论
1) 适当降低地下水位或者减小开挖坡角都可以提高边坡的稳定性。
2) 确定一区在不考虑降水时的最佳开挖坡角为45°,若是在降水容易、岩体开挖困难的情况下,可以通过降水增加开挖边坡角度,从而减小挖方量,且此研究对该矿的其他区域具有重要的借鉴意义。
3) 露天矿的开挖坡角对岩体挖方量至关重要,通过降低地下水位增加开挖坡角的角度可明显较少挖方量,且对采矿效率有明显的提高。
4) 地下水位对边坡的稳定性具有重要影响,建议在边坡形成后,设置有效的明排水系统,以减少雨季大气降水后形成的地表水对边坡的直接入渗和破坏。
