ARIA密码的积分故障分析

沈煜，李玮,,3,，谷大武，吴益鑫，曹珊，刘亚，刘志强，周志洪

（1. 东华大学计算机科学与技术学院，上海 201620；2. 上海交通大学计算机科学与工程系，上海 200240；3. 上海市可扩展计算与系统重点实验室，上海 200240；4. 上海市信息安全综合管理技术研究重点实验室，上海 200240；5. 上海理工大学计算机科学与工程系，上海 200093）

1 引言

分组密码作为实现消息保密、数据完整性保护和实体认证的核心基础体制，其设计、分析与实现方法一直是密码学研究的主流，在信息系统的安全领域发挥着重要的应用。ARIA算法是韩国国家安全研究所于 2003年提出的一种符合高级加密算法征集标准的分组密码，并且被商业部、工业部和能源部确认为国家标准分组密码，保障信息系统的数据安全[1-3]。研究表明，ARIA算法对差分分析法、线性分析法、截段–高阶差分分析法、不可能差分分析法、滑动攻击法、积分攻击法等密码分析方法具有足够的安全冗余[4-8]，具有优良的软硬件实现效率，在处理器应用上具有良好的实现性能。

然而，在现实环境中，只从ARIA算法的数学模型研究其安全性已经远远不够，必须从实现角度来考虑，即使密码算法在传统密码分析方法下是安全的，如果不能在运行平台上安全地加以实现，也不能正常发挥出预期作用。与传统的保密通信环境相比，如今的运行环境通常面临着更大的安全威胁。譬如银行卡、手持无线设备、汽车遥控锁、交通卡、门禁卡等密码载体的持有者不仅可以是正常用户，也可以是攻击者。攻击者借助异常时钟、微波辐射、激光照射等方式干预密码变换的正常过程，导致运算过程中发生错误，产生错误的输出结果，这种攻击方式比传统密码分析破译速度更快，有效地达到密码算法内关键数据的复制、篡改或伪造的目的，通常被称为故障分析[9-12]，由于其良好的攻击效果和潜在的发展前景，已成为密码分析和密码工程领域发展广受关注的方向之一。

故障分析在发展中逐步衍生出多种攻击方法，Biham等[13]于 1997年提出的差分故障分析法是目前分析范围最广、威胁最大且发展最迅速的一种攻击技术，被广泛应用于密码芯片的安全性研究中。之后，无效故障分析法、碰撞故障分析法、不可能故障分析法等故障攻击方法应运而生，这些方法充分结合了传统密码分析方法及软硬件实现技术，在实际运行环境中具有更加广阔的应用前景。但是，这些故障攻击方法的故障导入范围局限于最后若干轮，攻击轮数范围有限。

积分故障分析法是利用积分关系深入密码算法内部达到最深轮数的攻击方法，易于在物联网等应用中实现，攻击者通过分析内部状态的积分关系，便可以较低的计算量和存储量推导出正确的密钥。目前，国内外关于ARIA算法抵抗积分故障攻击的安全性尚未有公开发表的成果。因此，本文提出了一种针对 ARIA算法的新型积分故障分析方法，可以借助异常时钟、微波辐射、激光照射等方式使ARIA算法内部发生错误，达到扩大攻击范围并破译原始密钥的目的。所提方法对提升各类高端智能卡系统的防护与破译能力，具有重要的理论和实际意义。

2 研究背景

1997年，Boneh等[14-15]利用随机故障法成功破译了公钥密码算法，此后故障分析法在评测密码体制安全性的方法中拥有重要地位。随着故障注入精度及软硬件逆向技术的不断提高，对密码载体成功实施故障攻击所依赖的前提条件不断减弱，成本不断下降，故障分析环境已经可以在一定程度上被控制，这使故障分析法逐步发展为攻击主要密码体制的较为容易实施且最难防御的一种攻击技术[16-19]。

目前已有的针对ARIA算法的故障分析方法均为差分故障分析法[20-22]。在攻击过程中，攻击者首先将故障导入ARIA算法的最后两轮来恢复最后一轮的子密钥，然后对正确的密文进行解密，以获得最后一轮的输入，即倒数第2轮的输出，重复以上步骤来恢复最后4轮的子密钥，直至破译原始密钥为止。国内外的最新研究结果均集中于在ARIA算法的倒数第2轮导入随机字节故障来恢复最后一轮的子密钥。2008年，Li等[20]首次提出了针对ARIA算法的面向随机单字节故障模型的差分故障分析法。后来，Park等[21]在相同故障模型下提出一种改进的差分故障分析法，利用线性层的差异性，实现以较少的故障来恢复最后一轮子密钥，提升了攻击效率。Kim等[22]提出了面向多字节的差分故障方法，达到以较少故障数破译最后一轮子密钥的目的。这些方法充分结合了传统的差分分析方法以及软硬件实现技术，提高了故障导入的效率。然而，在物联网的应用环境中，故障可以被导入在密码算法的任意轮数，如果故障导入点可以扩展到更大的轮数范围，那么故障分析具有更强的威胁能力，因此，研究ARIA算法的新型故障分析方法是非常必要的。

Phan等[23]于 2006年首次提出了针对 AES（advanced encryption standard）算法的积分故障攻击法。该方法通过选择明文攻击实现的前提条件，在AES算法运行的倒数第4轮中加入随机故障，使其执行某些错误的操作，产生错误的密文，利用中间数据的积分关系即可恢复最后一轮子密钥；然后解密密文，破译更多的子密钥，直到破译原始密钥。虽然ARIA算法与AES算法具有相同的算法结构，但是由于ARIA算法中多轮故障路径的扩散性和混乱性更加复杂, 大大增加了攻击的难度，所以针对ARIA算法的积分故障分析，国内外还未有文献发表。

本文提出了针对ARIA算法的新型积分故障分析，利用故障与子密钥之间的积分关系，构造了 2个不同的积分区分器，从而使故障可以导入在倒数第3轮和第4轮运算中，进一步扩展了积分故障分析的攻击范围。由于积分故障路径包含更多的轮数，因此攻击者能将故障导入ARIA算法的更深轮数。现有的针对ARIA算法的故障分析方法的对比如表1所示。

表1 针对ARIA算法的故障分析方法的对比

3 ARIA算法简介

ARIA算法是一种典型的具有代换置换网络结构的迭代型分组密码，其密钥长度为3种，分别是128 bit、192 bit和256 bit；分组长度为128 bit[3]；所对应的轮数分别为12轮、14轮和16轮，分别表示为ARIA-128、ARIA-192和ARIA-256，如表2所示。

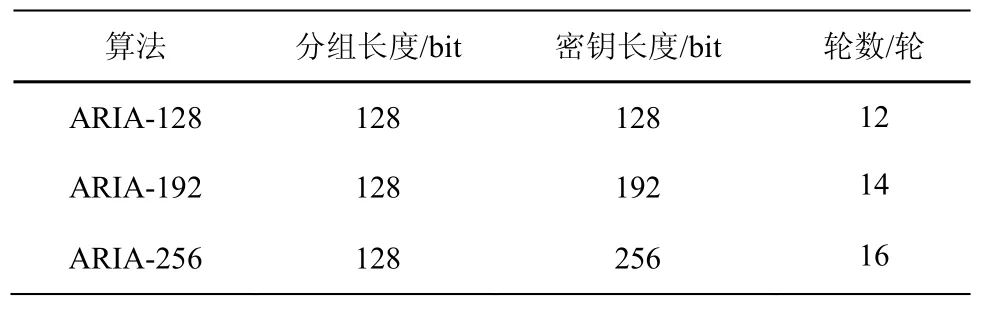
表2 ARIA算法的密钥长度和轮数的对应关系

ARIA算法由加密、解密和密钥编排这3个部分组成，其中，加密部分与解密部分的过程相同，不同之处在于子密钥的使用顺序。

3.1 符号说明

记 SL（substitution layer）和 DL（diffusion layer）分别为置换层运算和扩散层运算，SL-1和 DL-1分别为置换层和扩散层的逆运算。W0、W1、W2和W3是密钥编排方案中初始化部分产生的4个数据块。

3.2 ARIA算法描述

ARIA算法的结构如图1所示。

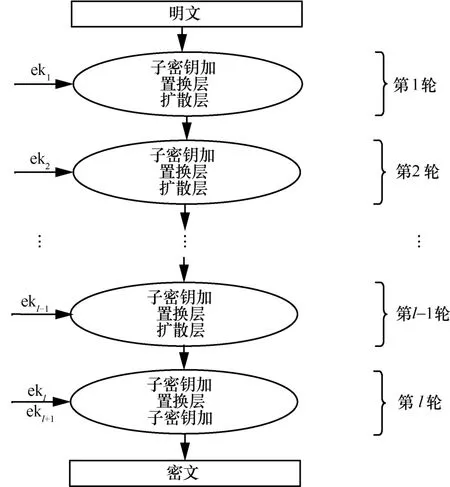
图1 ARIA算法的结构

1）子密钥加（RKA, round key addition）：子密钥与中间状态逐字节进行异或运算。

2）置换层：中间状态经过16个S盒进行置换，其中S盒有2种类型，分别用于奇轮数和偶轮数。

3）扩散层：对中间状态进行线性映射变换，通过与一个16×16的二进制矩阵C相乘实现，C如下所示。最后一轮中没有扩散层，被子密钥加运算所替代。

3.3 密码编排方案

密钥编排由初始化和子密钥生成这2个部分组成，具体如下。

1）初始化：4个 128 bit的数据块W0、W1、W2和W3通过原始密钥K基于3轮的Feistel网络结构而产生。

2）子密钥生成：通过W0、W1、W2和W3进行一系列异或运算、右移和左移操作，获得加密变换所需各轮子密钥。

4 ARIA算法的积分故障分析方法

4.1 故障假设和故障模型

故障假设表明了攻击者具备的能力，本文采用明文攻击，即攻击者可以任意选择明文进行处理，从而获得相对应的密文；故障模型表明了故障的状态，本文采用随机单字节模型，将单字节故障引入运算过程中某些轮的指定位置，并可以随机设定故障值。

4.2 主要过程

攻击者选择随机明文并使用同一个密钥进行加密，在运算过程中的某一轮中导入一组随机故障，从而获得一组错误的密文。故障导入既可以利用异常时钟、异常电流、微波辐射、激光照射、涡流磁场等手段通过真实的密码硬件来实现，也可以通过修改程序等软件模拟技术的方式来实现。攻击者通过构造合适的积分故障区分器，可以恢复最后一轮的子密钥；然后解密正确的密文，获得最后一轮的输入，即倒数第2轮的输出。重复上述过程，通过密钥编排方案直至破译原始密钥。

4.3 3轮攻击方案

针对ARIA算法，本文构造了一个2轮积分区分器，使得故障位置和子密钥恢复范围在3轮之间，从而可以破译ARIA算法，具体算法如图2所示。

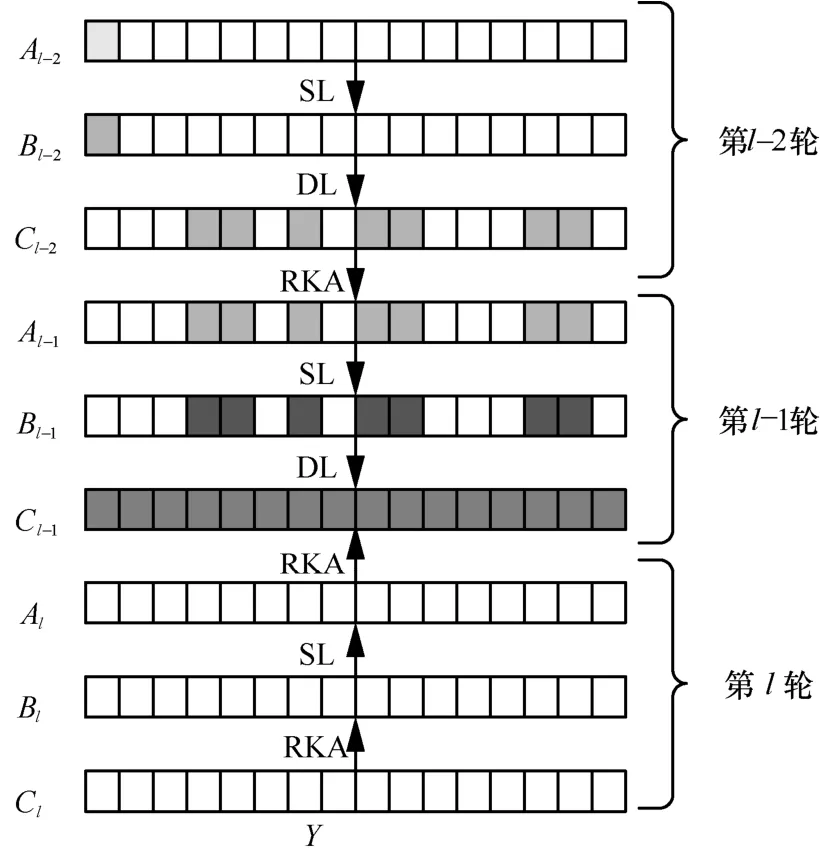
图2 故障导入在倒数第3轮的扩散路径

在构造积分区分器时，需要做以下定义。

定义 1如果定义在F2n上的集合对任意0≤u＜v≤2n-1，均有 α（u）≠ α（v），则称O为F上的活跃集[24]。

定义 2若定义在F2n上的集合对任意0≤u＜v≤ 2n-1，均有则称P为F上的稳定集[24]。

定义3若定义在F2n上的集合

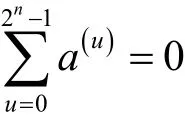
则称Q为F2n上的平衡集[24]。

攻击者为了构造ARIA算法的积分区分器，需要遵循以下性质：稳定/活跃字集通过双射（如可逆S盒，子密钥加）后，仍然是稳定/活跃的；2个活跃字集的和一定是平衡字集；稳定字集与活跃字集的和为活跃集；2个平衡字集的和为平衡字集。

结合上述定义和性质，攻击者可以追踪2轮运算中活跃字节的位置变化，如图2所示。具体路径为：第1轮中活跃字节通过扩散层变为7个活跃字节，然后这7个活跃字节经由第2轮扩散层变为16个活跃字节，这构成了第2轮扩散层输出中的一组集合；通过遍历该集合中所有字节值，使得第2轮的输出字节的积分之和为零。因此，在2轮积分区分器中，第2轮输出中的每个字节都是平衡的，并适用于第1轮中所有可能的活跃字节位置。

定理 1设多项式其中q是某个素数的方幂，则

定理 2若多项式是置换多项式，则aq-1=0 。

利用上述2个定理[25]来证明命题1中所构造的ARIA算法的2轮积分区分器的正确性。

命题1对于ARIA算法，如果第1轮输入中只有一个活跃字节而其他都是稳定字节，那么第 2轮输出中的所有字节都是平衡字节。

证明设 γ0, γ1,γ2,…,γ15为第1轮的输入字节，其中，只有一个字节β为变量，其他字节均为常量。假设 β=γ0，则第1轮的输入表示为

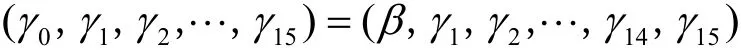
其中，β是变量，γ1,…,γ15均为常量。根据图2和表3中ARIA算法的运算特点，第1轮的输出可以表示为

第2轮的输出为

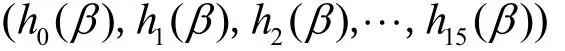
其中，h0（β）,… ,h15（β） 属于F28域上的置换多项式。第2轮输出中的每个字节都可以用F28上7个置换多项式的积分和来表示。

假设第2轮输出中的第一个字节为

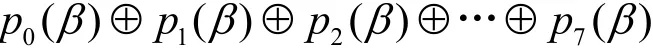
其中,p0（β）,…,p7（β）是F28上的置换多项式。结合置换多项式的性质，则有

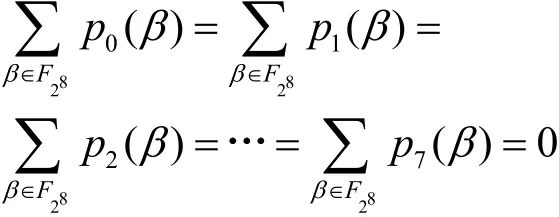
因此

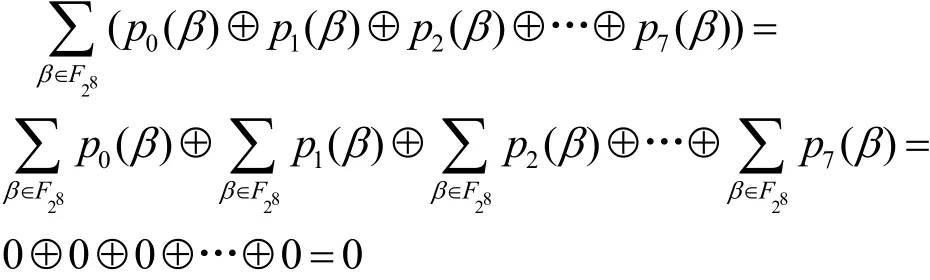
证毕。

根据2轮积分区分器，实现3轮攻击方案的具体步骤如下。

步骤1选择任意明文X，使用原始密钥K进行加密，并获得正确密文Y。

步骤2最后2轮子密钥ekl+1具有如下关系。

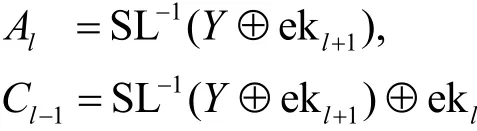
表3 ARIA算法的故障路径扩散

攻击者在加密算法的第l-2轮中的Al-2或Bl-2中导入随机故障，从而获得错误密文，如图2所示。在故障的导入过程中，均可以导致最后更多轮中发生变化，例如Cl-2、Al-1、Bl-2、Cl-1、Al、Bl、Cl等的字 节 变 化 会 导 致 出 现 ΔCl-2、 ΔAl-1、 ΔBl-2、 ΔCl-1、ΔAl、 ΔBl、ΔCl，最后生成错误密文。攻击者可以随机选择一个字节位置改变故障值，取值在[0,255]之间。因此，基于Cl-1的积分关系如下。

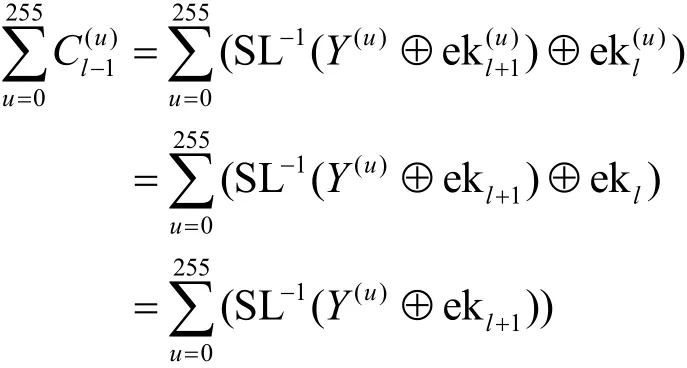
攻击者通过穷尽搜索ekl+1候选值的每个字节，然后结合同一个密钥和不同明文得到的正确和错误密文，进行重复操作，直到ekl+1候选集合中只有一个元素为止，即可求出正确的子密钥ekl+1。

步骤3假设故障被导入到第l-3轮，攻击者通过子密钥ekl+1对正确的密文进行解密最后一轮，得到lA。此时，lA既是最后一轮的输入，同时也是倒数第2轮的输出，因此

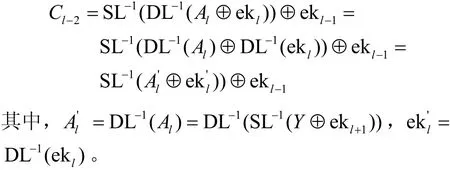
攻击者构建Cl-2的积分关系如下。

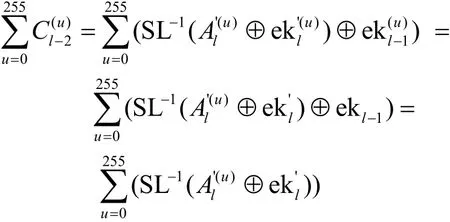
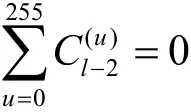
攻击者计算扩散层中Cl-2的总和，穷尽搜索中的每个字节值。利用即可推导出子密钥ekl。同理，通过将故障导入在第l-4轮和第l-5轮，攻击者可以分别恢复其他2个子密钥

步骤 4 结合密钥编排方案，攻击者通过最后4个子密钥，即可推导出ARIA算法的原始密钥。

4.4 4轮攻击方案

在上述3轮攻击方案中，攻击者可以对步骤2中的第l-2轮和步骤3中的第l-3轮、第l-4轮和第l-5轮分别导入故障，从而恢复最后4轮子密钥。然而，在轻量级环境中，随机故障可能发生在算法的其他轮中。如果将故障位置扩展到更多轮，则积分故障分析的实现范围更大。

结合命题2构建了2.5轮积分区分器，此时故障导入位置分别推广到步骤2中的第l-3轮和步骤3中的第l-4轮、第l-5轮和第l-6轮。此时故障位置和子密钥处于4轮运算范围内，因此称为4轮攻击方案，具体如图3所示。

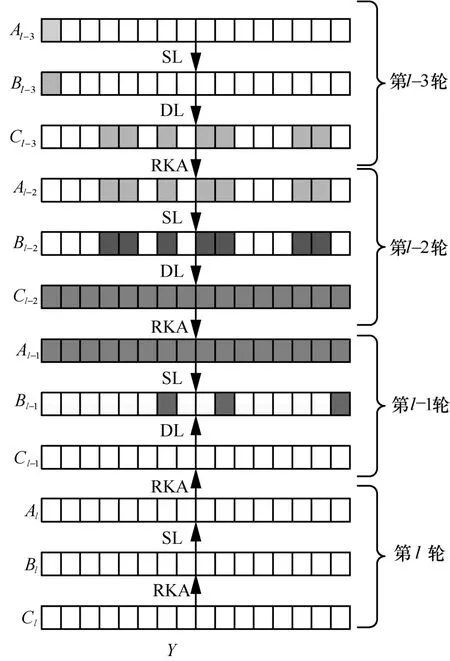
图3 故障导入在倒数第3.5轮的扩散路径

命题2对于ARIA算法，如果第1轮输入中只有一个活跃字节而其他都是稳定字节，则在第3轮替代层的输出存在3个平衡字节[5]。

4轮攻击方案采用了与3轮攻击方案相同的步骤1和步骤4，不同之处在于步骤2与步骤3。4轮攻击方案的步骤2故障导入在第l-3轮的Al-3或Bl-3，可知Bl-1中有3个字节的集合是平衡集，如表4所示，则有

表4 活跃字节和相应的3个平衡字节的位置列

此时，计算Dl-1可以转化为7个向量的异或，该步运算将数据复杂度由 2128降到 7 ×28。基于 2.5轮的积分区分器，Bl-1的第j个字集是平衡字集，因此有

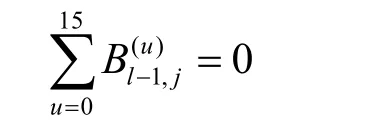
其中，j∈J。

在步骤3中，当故障导入在第l-4轮的Al-4或Bl-4时，可知Bl-2中有3个字节的集合是平衡集，并且

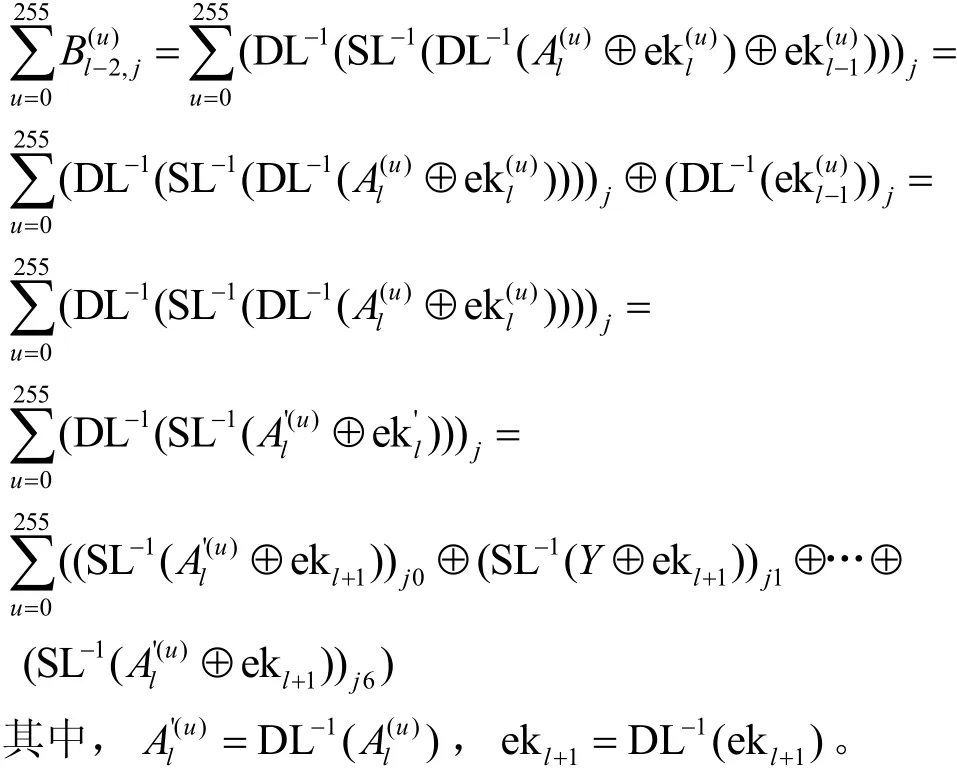
此时，j∈J，j0到j6的值如表4所示。同理有

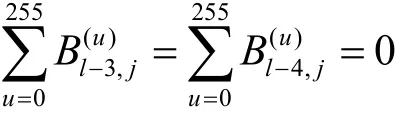
其中，0≤j≤1 5。攻击者可以依靠同一个密钥和不同明文得到的不同密文，利用穷尽搜索运算求出最后4轮子密钥。

5 理论时间复杂度

在上述分析过程中，为了计算平衡字节的积分和，攻击者至少需要一组密文，包括一个正确的密文和255个错误的密文。

设η表示一个错误的子密钥可以通过积分和检查的概率，θ表示攻击过程中穷尽搜索的子密钥空间。当攻击者诱导ι个密文集合时，子密钥候选项中剩余的错误子密钥数为（θ-1）ηι。如果（θ-1）ηι＜1，子密钥候选值集合中只有唯一值，即为正确的子密钥。

在3轮攻击方案中，存在

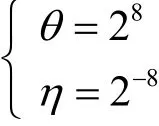
如果ι＞2，那么攻击者可以计算出真正的子密钥。此时穷尽搜索一组密文的时间复杂度是

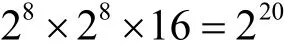
因而，破译ARIA算法的最少理论时间复杂度为

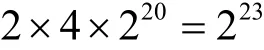
在4轮攻击方案中，存在

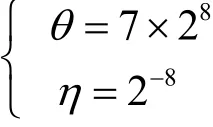
如果ι＞2，则攻击者可以推导出真正的子密钥。此时穷尽搜索一组密文的时间复杂度是

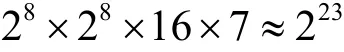
因而，恢复ARIA算法密钥的最少理论时间复杂度为

6 实验结果分析

实验环境为Inter Core I7-7700K@4.2GHz、内存为 32 GB的计算机，使用 Java语言编程进行ARIA算法的加解密和攻击操作。利用软件模拟故障产生，从而得到错误密文，本文共进行了 1 000次实验，将这些实验平均分成了 5组，记为G1、G2、G3、G4和G5。在积分故障分析过程中，攻击者至少需要一组密文，包含一个正确密文和255个错误密文。本节采用准确性、可靠性和耗费时间对实验结果进行了详细描述。

准确性是指候选密钥数与真实密钥数之间接近的程度。数值越接近，则实验结果就越准确。采用均方根误差（RMSE, root mean square error）计算式来进行计算。

其中，m为实验次数，e为第e次实验，φ'（e）为在第e次实验中已恢复出的候选子密钥的比特数，φ为真正子密钥的比特数。均方根值越接近于0，则实验结果就越准确，候选子密钥的均方根值如表5与表6所示，其中m=200，φ=128、e={ 1 , …, 2 00}。实验结果表明，在3轮和4轮攻击方案中，分别最多仅需要3组和16组密文集合即可恢复子密钥。

可靠性是指成功实验在所有实验中的比例。如表5与表6所示，在3轮攻击方案中，子密钥恢复的平均比例分别为0、94.8%和100%。在四轮攻击方案中，子密钥恢复的平均比例分别为0、0、…、0和100%。

表5 在3轮攻击方案中恢复子密钥的准确性和可靠性

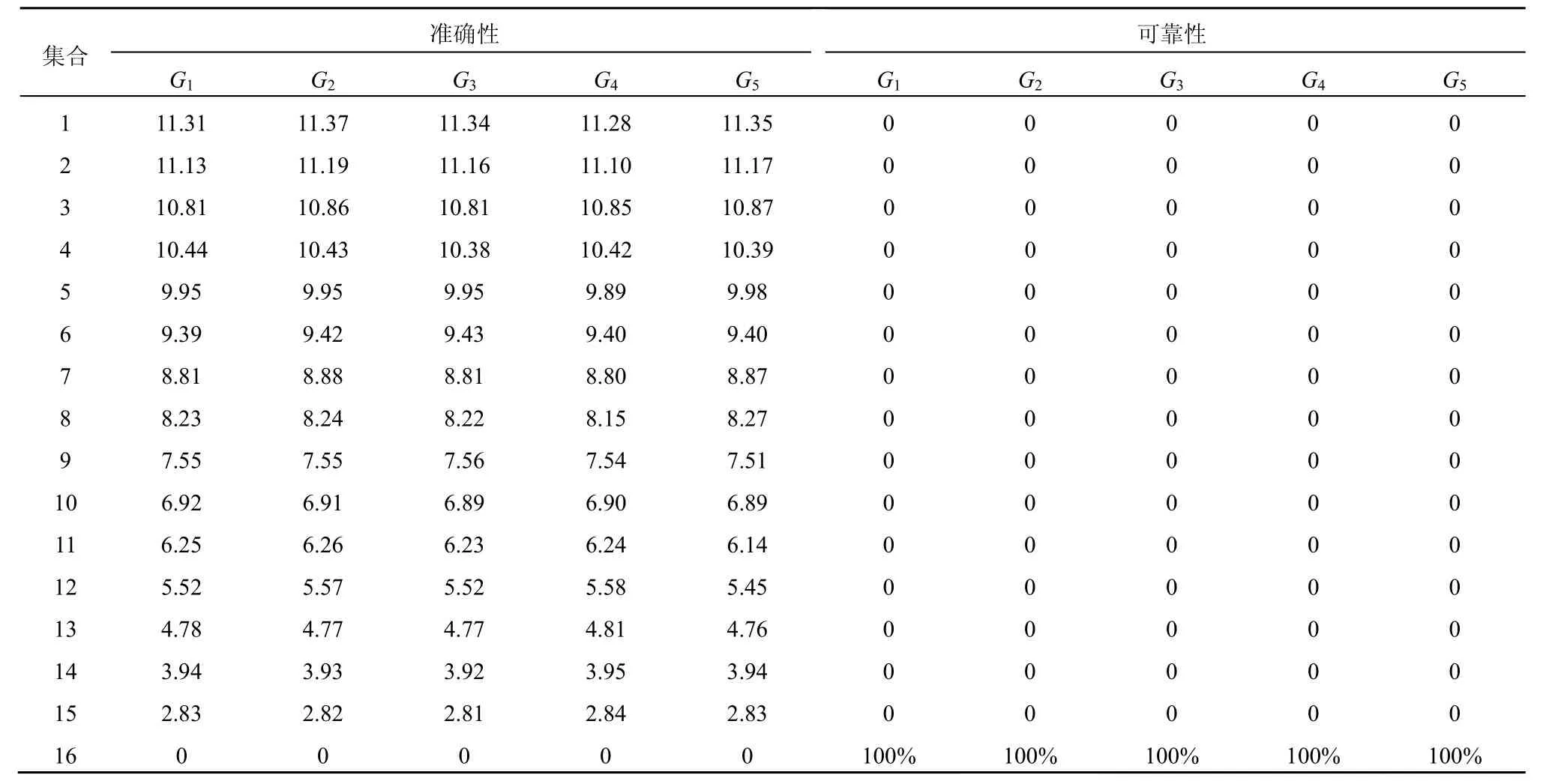
表6 在4轮攻击方案中恢复子密钥的准确性和可靠性

耗费时间是指从故障导入到恢复子密钥的时间。图4显示了1 000次实验的耗时。在3轮攻击方案中，97.7%的耗费时间处于5～10 s之间，而在4轮攻击方案中，87%的耗费时间处于30～40 s之间。

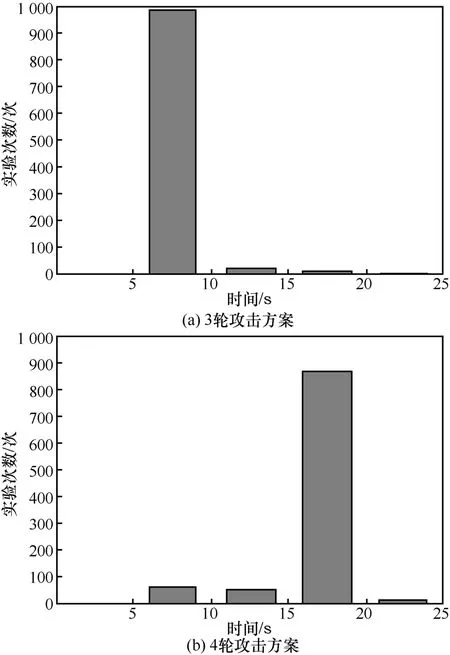
图4 在攻击方案中恢复子密钥的耗费时间

因此，在3轮攻击和4轮攻击方案中，穷尽搜索一组密文的实际时间复杂度分别为

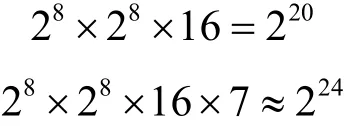
则恢复ARIA原始密钥的最少实际时间复杂度分别为

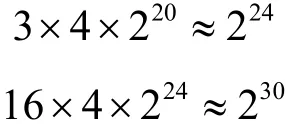
7 结束语

本文提出了基于ARIA密码的积分故障分析方法。理论分析和实验结果表明，在面向单字节的故障模型中，分别可以构建2个积分区分器进行故障导入来破译ARIA算法。相较于其他故障分析方法，积分故障分析可以进一步深入算法内部更深轮数进行攻击，在攻击范围上均具有显著的优势。因此，以ARIA为代表的标准密码在现实环境中实现时必须加以软硬件防护措施进行保护，否则极易受到积分故障分析的威胁。