基于EM算法的离散-连续型混合分布参数估计

冯 杭，王胜兵

（海军工程大学 理学院，武汉 430033）

0 引言

随着计算机技术和信息技术的不断提高，如何从大量复杂多变的数据中提取有用的信息、模式和知识成为亟待解决的问题。在实际问题中，传统的单一模型已经无法满足正确性和准确性的要求，有限混合分布[1]的提出为大量随机现象建立统计模型提供了数学基础。混合模型可以定义极其复杂的概率密度函数，是分析复杂现象的一个极其重要的工具，从图像分割技术到股票市场的数据分析，它几乎涵盖了金融、经济、生物、医学、计算机科学及工程领域等的各个学科[2]。

实际中常用数据拟合方法对混合模型的参数进行估计，由于混合模型的密度函数较复杂，待估计参数较多，一般的数据拟合方法无法准确估计出混合模型的参数值。EM算法是一种被广泛用于最大似然估计的迭代算法[3]，可以对混合模型进行参数估计，还可以用于混合模型的聚类分析。近年来，国内外研究者对EM算法作了大量的研究。Gelffrey[4]利用EM算法讨论了有限正态分布的混合模型；孟俊才[5]推导出一些离散型混合分布模型中的参数迭代公式；陈文强[6]利用矩估计法和聚类法研究了处于不同形式下的混合泊松分布的参数估计。

本文针对离散-连续型混合分布参数估计的问题，利用EM算法和极大似然估计原理，给出未知参数的似然函数，推导出参数估计时需要用到的Q函数以及各未知参数的更新公式，并给出了EM算法的流程图。利用EM算法进行数值模拟仿真实验，检验EM算法在解决这类问题时的有效性。

1 连续型与离散型分布混合模型

以正态分布和泊松分布混合为例。假设有观测数据y1，y2，…，yn，这些观测数据来自一个由g1个正态分布和g2个泊松分布混合而成的混合分布，该混合分布的分量的权重记为 π1，π2，…，πg1+g2，其和为1。则观测数据yi的混合密度可以表示为：

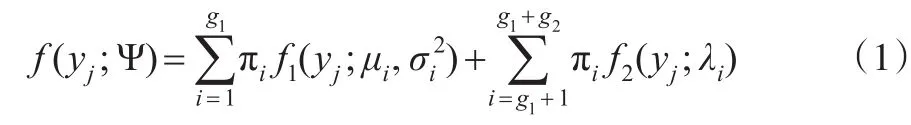
其中分量密度：

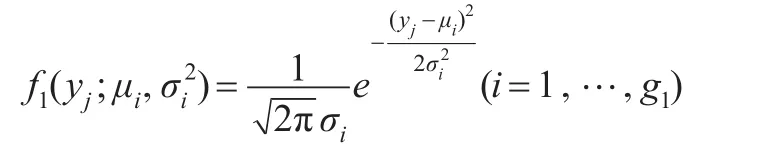
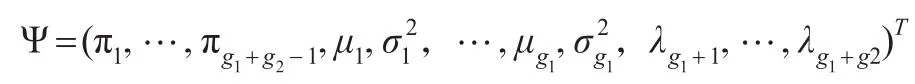
至此，有限混合模型的估计归结为对参数向量Ψ的估计。借助于极大似然（ML）估计方法，可以将该问题转化为一个最优化问题，其优化的目标函数是似然度L(Ψ)或者等价对数似然度logL(Ψ)，其定义域是整个参数取值空间。

未知参数的似然函数为：

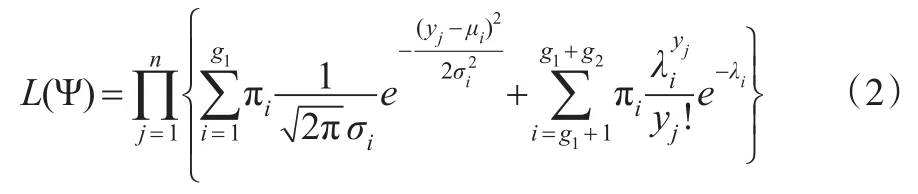
对数似然函数为：

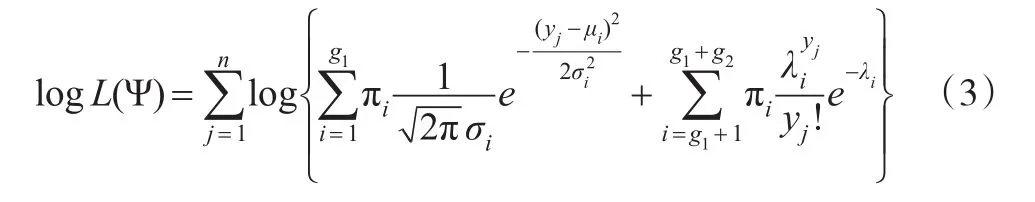
2 EM算法框架下的参数估计

对于混合分布而言，仅从数据本身难以分辨每一个样本值yj来自哪个分布，从这个意义上看，观测值中并不包含数据的全部信息，是“不完整数据”。在EM框架下，每个yj被认为来自混合模型的其中一个分量。用z1，z2，…，zn表示不可观测的分量指示向量，其中：

用y=(y1，y2，…，yn)T表示观测数据向量，用z表示缺失数据向量，则x=(yT，zT)T表示完整数据向量。

在有限混合分布模型中，基于参数Ψ的完整数据对数似然度为：

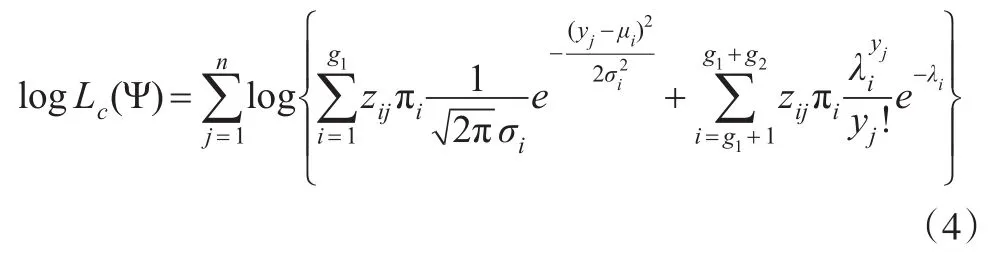
EM算法的每次迭代包含两个步骤：期望步骤（E-Step）和最大化步骤（M-Step）。算法通过对“含完整数据”的对数似然函数值logLc(Ψ)的逐步迭代计算来求解“含不完整数据”的式（3）。由于logLc(Ψ)依赖于不可观测的缺失数据z，所以在期望步骤中将logLc(Ψ)用所谓的Q函数来代替。

期望步骤：计算Q函数Q(Ψ;Ψ(k))。

在EM算法的第k+1次迭代中：

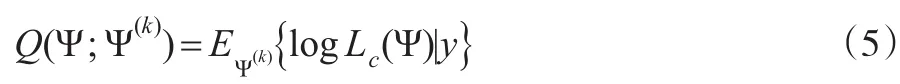
这是在给定y和当前Ψ(k)时完整数据对数似然度的条件期望。

记对应zij的随机变量为Zij，由于完整对数似然度关于缺失数据Zij是线性的，所以，借助可观测数据y，就能简单地计算出随机变量Zij当前的条件期望，即：

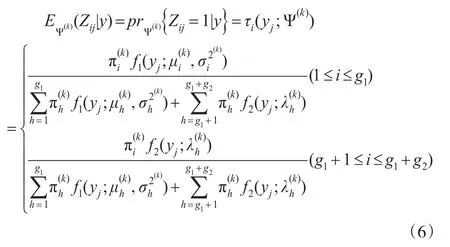
其中τi(yj;Ψ(k))是第j个可观测数据yj属于有限混合分布的第i个分量的后验概率。从式（5）和式（6）可得：

最大化步骤的任务则是更新Ψ的估计值Ψ(k+1)，从而使得Ψ的整个参数空间上Q(Ψ;Ψ(k))函数取最大值。

最大化步骤:更新Ψ的估计值Ψ(k+1)。

由公式(7)分别对 πi、μi、σi2和λi求导，可得最大化步骤中需要用到的参数迭代公式：

利用EM算法进行参数估计的流程如下页图1所示。

3 数值模拟实验

本文以正态分布和泊松分布的混合模型为例，利用matlab软件，按照以下步骤进行混合分布参数估计的数值模拟实验：

步骤1：设计并生成实验数据，生成n个服从相应混合分布的随机数；

步骤2：给定初值Ψ(0)；

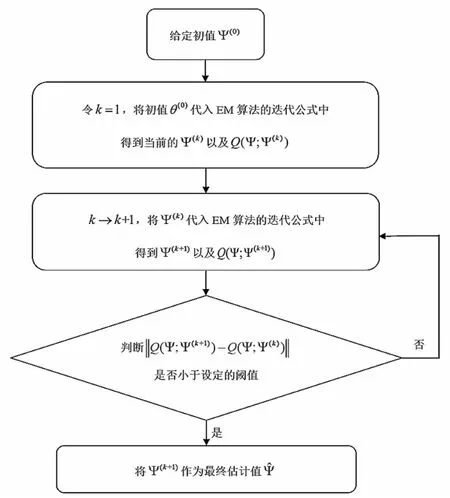
图1 EM算法流程图

步骤4：画图验证并进行误差分析。

建立二阶正态分布和二阶泊松分布混合分布模型0.15N(5，12)+0.35Π(8，1.22)+0.15E(5)+0.35E(8)，产生1000个来自该模型的随机数，并选取以下四组不同的初值（第一组初值为原混合模型各参数理论值）。

Ψ(0)=(0.15，0.35，0.15，5，12，8，1.22，5，8)

Ψ(0)=(0.1，0.2，0.3，1，12，2，12，0.1，0.2)

Ψ(0)=(0.3，0.2，0.3，3，12，6，12，0.3，0.4)

Ψ(0)=(0.25，0.25，0.25，5，12，10，12，0.5，0.6)

进行数值模拟，并设定阈值为10-3。

参数估计的结果如表1所示。

表1 混合正态分布和泊松分布参数估计结果

3.1 有效性验证

由表1可知，实验1选取的初值为原混合模型各参数的理论值，通过对此结果进行验证，可以直观的看出EM算法对于多种分布混合的参数估计的有效性。

将由EM算法得到的混合分布各个分量的参数的估计值与理论值进行比较，结果如图2所示。

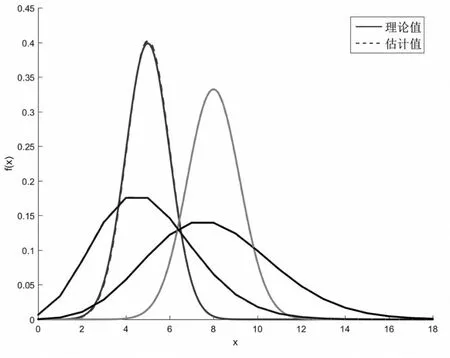
图2 实验1各个分量的参数估计结果

由图2可以直观的看出，各个分量的参数的理论值曲线与估计值曲线的贴合程度很高，说明EM算法能够在很大程度上还原混合正态分布和泊松分布的各个分量的参数，从而证明该算法的有效性。

将由EM算法得到的混合分布即估计值与理论值进行比较，结果如图3所示。

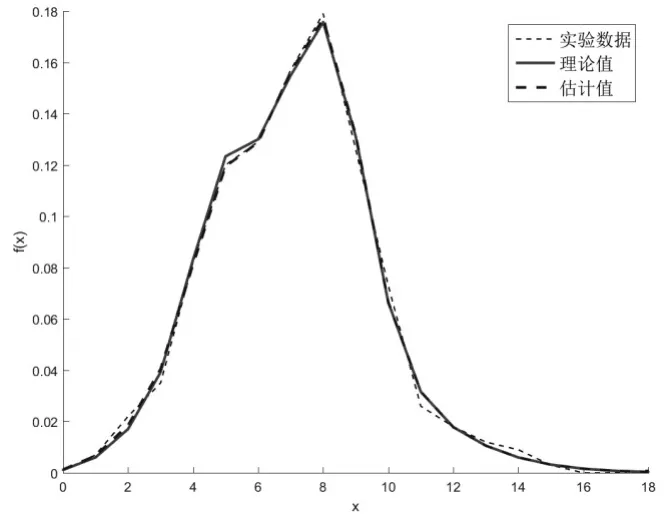
图3 实验1整体估计结果

由图3可以直观的看出，EM算法能够在很大程度上还原混合多种连续型与离散型分布的参数，从而证明该算法的有效性。同时由图3可以看到，估计出的结果与最初选取的理论值之间存在一定的差异，究其原因有以下两点：

（1）利用EM算法进行迭代计算过程中，涉及到小数有效数字位数的选取问题，因此存在一定的误差；

（2）matlab生成的随机数据是离散的，在数据个数有限的情况下进行数据的统计还原时，无法得到和理论值完全相同的分布函数。

但正是由于以上原因导致的误差存在，实验数据在一定程度上说明了，初始参数在某些范围变化的时候，参数估计值几乎是相同的，说明此时得到的估计值是对数似然度函数的一个稳定点，进一步证明了EM算法的有效性。

3.2 敏感性分析

由表1中实验2、3、4对比可知，各个参数初值的不同会影响估计值的准确程度，因此对于3组实验分别进行验证。

以实验4为例，将由EM算法得到的混合分布各个分量的估计值与理论值进行比较，结果如图4所示。

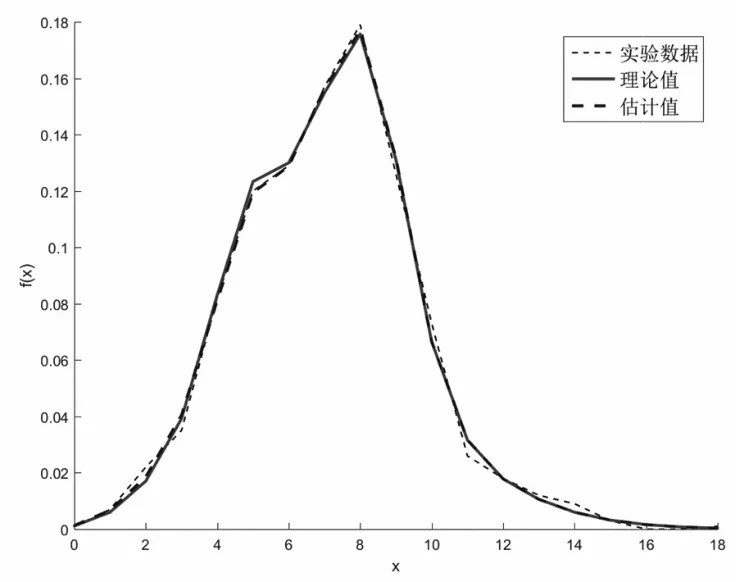
图4 实验4各个分量的参数估计结果

由图4可以看出，各个分量的参数估计值曲线与理论值曲线贴合程度较差，说明当超过某一范围时，初值的改变会使得迭代结果发生较大改变，从另一方面说明了计算结果对于初值的选取是敏感的。

3.3 结果分析

根据上述实验结果可知：

（1）利用EM算法估计出的参数值能够较好地还原多种分布混合中各分量分布的参数，证明了该算法的有效性。

（2）初始参数在某一范围变化时，参数的估计值几乎是不变的，说明此时得到的估计值是对数似然度函数的一个稳定点。

（3）超出某一变化范围之后，某些初始值会使得迭代结果发生较大改变，说明计算结果对于初值的选取具有敏感性。

4 结束语

本文利用EM算法，针对离散-连续型混合分布参数估计的问题，以正态分布和泊松分布混合为例，进行了数值模拟实验，并验证了EM算法可以有效解决这类问题。但同时发现了EM算法的估计精度受初始值的影响很大这一缺陷，下一步将引入常见的智能优化算法对初始值敏感问题进行改善。