基于邻域互信息的区间DEA交叉效率评价方法

范建平，赵 苗，吴美琴

（山西大学 经济与管理学院，太原 030006）

0 引言

数据包络分析（DEA）是Charnes等[1]于1978年提出的，它是对一组具有多投入多产出的决策单元（DMU）进行相对有效性评价的非参数方法。传统的CCR模型是基于自评的角度出发，这样会高估决策单元的效率并很难做到完全排序[2]，Sexton等[3]提出了DEA的交叉效率评价方法，该方法同时考虑了自评与他评，在一定程度上解决了CCR不能完全排序的问题，但是也存在一定的缺陷，即交叉效率不唯一。Doyle等[4]将二级目标的概念引入到DEA中，提出了仁慈型模型和进取型模型，目标函数为最小化或最大化其他所有决策单元构成的假想决策单元的效率分数，基于此Jahanshahloo等[5]在Doyle模型的基础上将目标函数改为最大化或者最小化被评决策单元的效率分数。但是其所提的两个模型都比较极端，认为所有的决策单元之间要么是竞争的关系要么是合作的关系，并且没有给出在什么样的情况下应该采取什么样的策略的选择依据。杨锋等[6]提出了竞合交叉效率模型，同时考虑了决策单元之间竞争与合作的关系，通过聚类分析将决策单元进行分类，如果分为一类则为合作关系，两者之间采用仁慈型模型，反之采取进取型模型。关于交叉效率方法的改进有很多文献，李春好等[7]参照TOPSIS的理想点构造方法对DEA交叉效率模型进行改进，范建平等[8]将熵和误差传递引入到区间DEA中，Bagherikahvarin等[9]结合了DEA和偏好顺序结构评估法（PROMETHEE II），对DEA的权重稳定区间进行约束，王庆等[10]给出了考虑相关系数的DEA共识度交叉效率评价方法。

本文在DEA交叉效率模型中加入了邻域互信息和潜在信息函数，首先对区间数运用变量替换法分别利用进取型、仁慈型和竞合交叉三个模型进行求解，这样就避免了选择策略的极端化问题，在竞合模型中利用邻域互信息进行分组，充分运用了数据本身的特征，分组更客观。这里因三个模型其思路有差别，很有可能出现排名不一致或者不能完全排序的问题。之后利用潜在信息函数在处理小样本数据时的优势来对区间效率进行集结。潜在信息函数可以对现有的区间进行扩展，并且它认为处于中间位置的数值出现的概率更大，这也正与上述三个模型的原理相吻合，因为进取型和仁慈型认为所有的决策单元之间要么竞争要么合作，而竞合模型同时考虑竞争与合作更符合现实，所以其模型效率值出现的概率更大。运用潜在信息函数求得每个决策单元在三个模型下的不同权重，运用OWA算子进行集结，求得每个决策单元的最终效率值，并且对决策单元进行排名。

1 理论模型

1.1 DEA模型

1.1.1 传统的DEA交叉效率

假定有n个决策单元，每个决策单元均有m种不同的投入和s种不同的产出，用xij表示第j(j=1，2，…，n)个决策单元的第i(i=1，2，…，m)种投入，用yrj表示第j(j=1，2，…，m)个决策单元的第r(r=1，2，…，s)种产出，对于被评价的决策单元DMUd，求解其效率Edd的CCR线性规划模型如下：

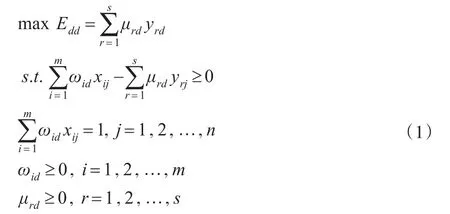
其中，ωid(i=1，2，…，m)表示投入向量的权重系数，μrd(r=1，2，…，s)表示产出向量的权重系数。求解上述模型（1）得到决策单元DMUd的效率值Edd，以及最优投入权系数和最优产出权系数。求解模型n次就可以得到n个决策单元的自评效率值以及对应的最优权系数。在自评时通常会出现多个决策单元的效率值均为1，无法进行充分排序，于是Sexton等[3]提出了交叉评价的思想，利用DMUd的最优权重来评价DMUj的他评效率这样就可以获得n个决策单元的他评效率。对于任何一个决策单元，通过求解公式就可以得到每个DMU的交叉效率。

1.1.2 进取型模型和仁慈型模型

本文采用Jahanshahloo等[5]提出的对Doyle等[4]二级目标模型进行改进的进取型和仁慈型模型，其改进的仁慈型模型为在使自评效率分数保持最大的情形下，最大化被评决策单元的效率分数，对应的模型如下所示：

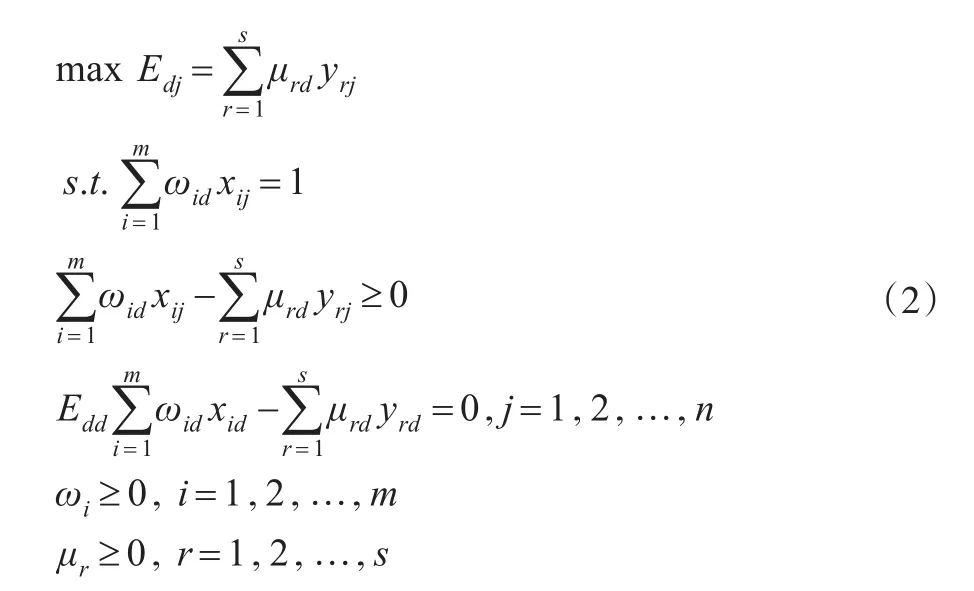
类似的，Jahanshahloo等[5]提出的改进的进取型模型是在保持自评效率最大的情况下，将目标函数改为最小化被评决策单元的效率分数。具体的模型为：

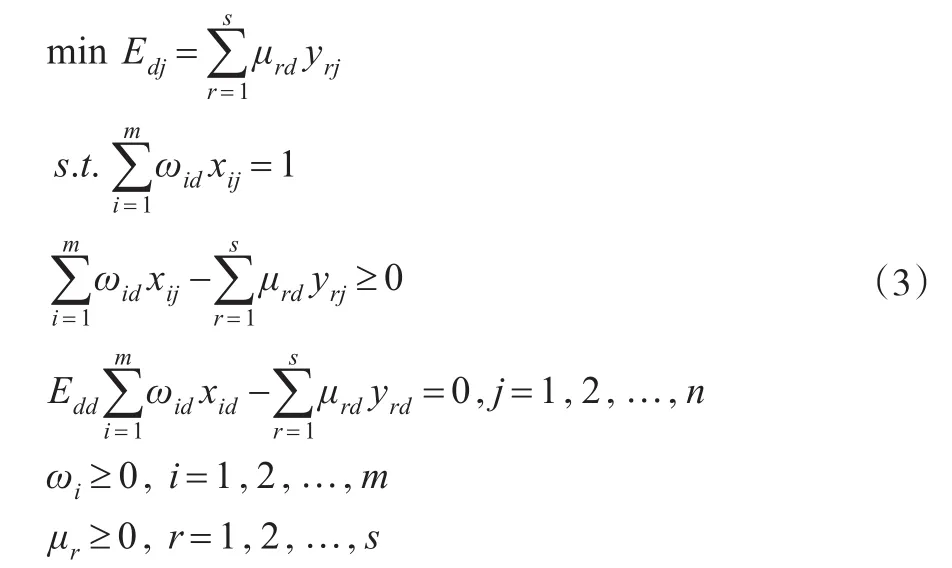
模型（2）和模型（3）中的Edd是DMUd自评效率分数，是由CCR模型（1）求得的，而Edj是他评效率分数，在求出1个自评效率分数和（n-1）个他评效率分数后通过求和平均就可以求每个决策单元对应的交叉效率分数。

1.1.3 竞合交叉效率模型

杨锋等[6]在Jahanshahloo等[5]模型的基础上同时考虑决策单元之间竞争与合作的关系提出了竞合交叉效率的模型，将决策单元利用聚类分析分为H类，设所有的决策单元的集合为Tt(t=1，2，…，H)，若两个决策单元为同一类则是盟友，采取合作的关系，否则为竞争关系的敌友关系。其思想是在保持自身效率最大的情况下最大化盟友的效率且最小化敌友的效率，线性规划模型如下所示：

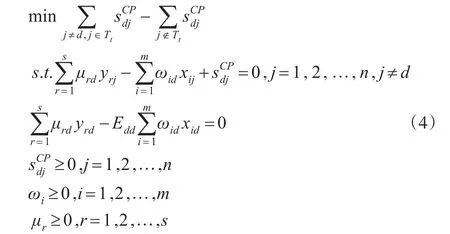
通过求解模型（4）就可以求得竞合模型的他评效率分数，然后再用与1.1.2中相同的方法得到每个决策单元的交叉效率分数。

1.2 邻域互信息

1.2.1 熵和互信息

在信息论中，互信息是用来测量一组样本在两个属性上的相关程度的一种方法，常被用于特征选择和决策树问题中。互信息是由在Shannon[11]提出熵的概念之后出现的，它可以用来测量两个随机变量之间的相关性。下面给出熵和互信息的相关定义：

定义1[12]：A={a1，a2，…，an}是一组离散随机变量，ai的概率为p(ai)，A的熵定义为

定义 2[12]：如果B={b1，b2，…，bm} 也是一组离散随机变量，那么A和B的联合熵为logp(ai，bj)。

定义3[12]：A和B的互信息可以表示为MI(A;B)

1.2.2 邻域互信息

Shannon熵和互信息很难估计数值型数据的概率分布，故其不能用来测量数值型数据的相关性，Hu等对Shannon熵进行了扩展，进而提出了邻域互信息的概念，可以用来处理数值型数据，并将其应用到医学邻域[13]，用于癌症基因的选择，并且从离散数据扩展到连续数据，同时Legg等[14]将邻域互信息运用到眼底成像问题中。下面给出邻域互信息的相关定义和性质。

定义4[12]：U是一个样本集，xi∈ℜN，Δ是U上的一个距离函数。δ≥0，可以定义样本x的邻域为δ(x)={xi|Δ(x，xi)≤δ}。

定义5[12]：U为一个样本集，S为该样本的一个属性，那么样本xi在S上的邻域表示为δS(xi)。xi的邻域不确定为样本集的平均不确定表示为

定义6[12]：R，S⊆F是两个属性子集，样本集xi在S∪R子空间上的邻域表示为δR∪S(xi)，那么样本集在属性R和S上的邻域互信息可以表示为NMIδ(R;S)=

1.3 潜在信息函数

在多属性群决策问题中，不同的专家对若干个备选方案的评价结果就可以构成一个样本集，该样本中有的元素可能会相对较大或较小，赋予这些元素的权重往往较小，相对应地，处于中间位置的元素往往更贴近现实，权重更大，因此就有很多基于正态分布的方法[15]用来求对应的权重，因为通常当样本数量较大时，基于正态分布的方法是合理的，但是当样本集较小时，上述方法将不可行，就需要对已有的数据范围进行扩展，于是就提出了潜在信息（LI）函数，本文通过现有数据及其在该组数据中所处的位置来求得该组数据的增长趋势（IT）和下降趋势（DT）以此对现有数据集进行扩展，并求得该组数据的偏好值，并通过该偏好值得到每个元素的权重。Chang等[16]利用潜在信息函数提高了小样本的预测能力。而Wu等[17]利用潜在信息函数与OWA算子结合起来对区间样本数进行排名。利用潜在信息函数求权重的计算步骤[17]如下：

步骤1：给定一组数据集X={x1，x2，…，xn}，那么这组数据的范围（range，R）表示为：R=xmax-xmin。

步骤5：求得扩展的上界（UB）和下界（LB）：UB=xmax，其中表示集合中的

步骤6：这样CT，UB和LB就形成了一个三角潜在信息函数，根据三角函数的性质，类似地，求出该组数据的潜在信息值νk(k=1，2，…，n)：

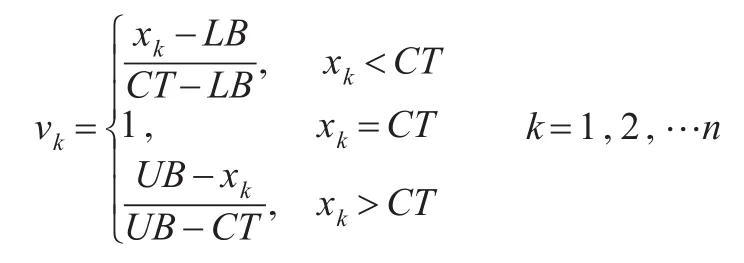
步骤7：对νk进行归一化处理，得到每个元素xk对应的权重

2 计算方法

本文所提的区间DEA交叉效率评价方法中集合了邻域互信息和潜在信息函数，具体的计算过程如下：

首先，基于投入产出的区间数用变量替换法根据模型（2）和模型（3）进行求解，分别得到仁慈型和进取型的效率分数。接着，基于定义6，得到决策单元两两之间在所有投入产出指标之间的邻域互信息，然后对决策单元进行分组，再运用模型（4）求得竞合交叉效率分数。在这里，已有的文献均采用的是单值的邻域互信息，本文的投入产出指标数据是区间值，提出的区间值的距离计算公式如下所示：

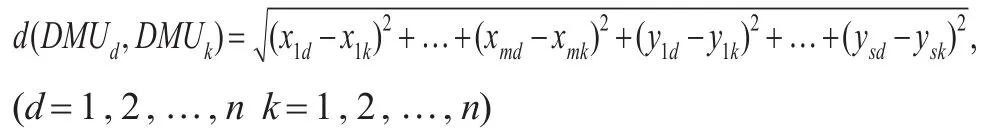
其次，将上一步求得的每个决策单元的三个效率分数看作一个样本，由于竞合交叉效率同时考虑了决策单元之间竞争与合作的关系，与进取和仁慈型模型相比，竞合模型得到的效率值位于进取型和仁慈型模型区间内，更符合现实，所以其出现的概率较大。

然后，上述得到的三个效率分数可能会出现排名不一致或者不能充分排名的问题。于是需要对三个效率分数进行集结。而潜在函数在处理小样本时相对比较合理，样本较小时根据潜在信息函数对样本进行一定的扩展，使数据的范围扩大，根据1.3中相对应的公式可以得到数据的中心值（CT）、上限（UB）和下限（LB）以及中心位置（CT）、增长趋势（IT）和下降趋势（DT），中心值、上限和下限就形成了一个三角潜在信息函数，进而得到每个DMU的潜在信息值以及每个DMU所对应的三个模型的权重。

最后，根据OWA算子对每个决策单元的三个效率分数进行加权平均，就可以求得每个决策单元最后的一个集结的效率分数，并根据该效率分数进行排名。

3 算例

本文采用Despotis等[18]用到的算例，包含5个决策单元，有两个投入和两个产出，并且投入和产出都是以区间值给出。具体数据见表1所示。

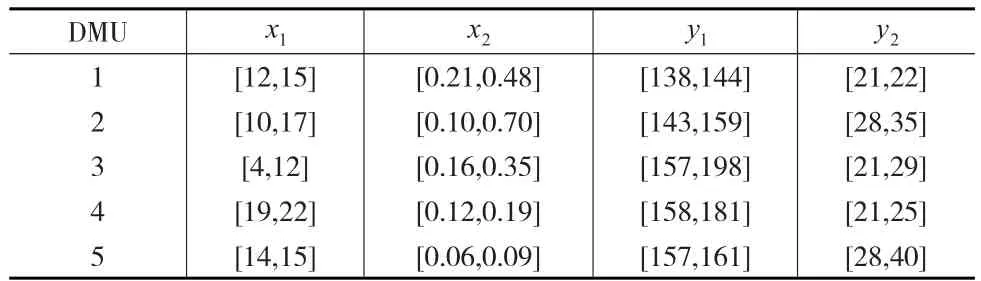
表1 原始数据

根据变量替换法[19]运用MATLAB软件分别对模型（2）至模型（4）求解，得到5个DMUs的进取型、仁慈型、竞合交叉效率分数，这里根据区间值邻域互信息分组，得到决策单元1与3、3与4和3与5是合作的关系，其余的均是竞争的关系，结果如表2所示。

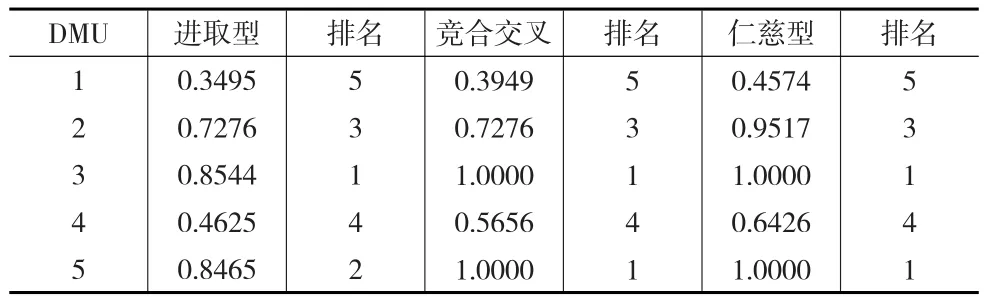
表2 三个模型下的效率分数和排名

从表2中可以看到进取型模型的效率分数均比较低，仁慈型模型的效率分数最高，而竞合模型的分数处于中间位置，并且因分组中DMU2与其他DMUs均是竞争的关系，所以DMU2的进取型效率分数应与竞合模型的效率分数相同，而通过模型的计算结果也一致，说明将邻域互信息运用到DEA交叉效率中是合理的，也说明了本文提出的区间邻域互信息计算的正确性。

由于竞合交叉效率和仁慈型模型得到DMU3和DMU5均是有效的，不能完全排序。故根据1.3中关于潜在信息函数计算的步骤分别求得各个DMU的中心趋势、下界和上界以及根据公式求得各DMU在三个模型下不同的权重，结果见表3所示。

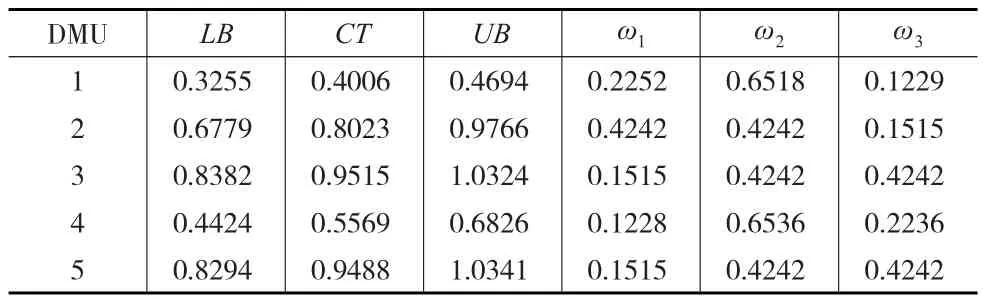
表3 潜在信息函数中的相关值

最后根据OWA算子对效率分数进行集结，求得各个DMU的最终集结效率值，最后的结果如表4所示。

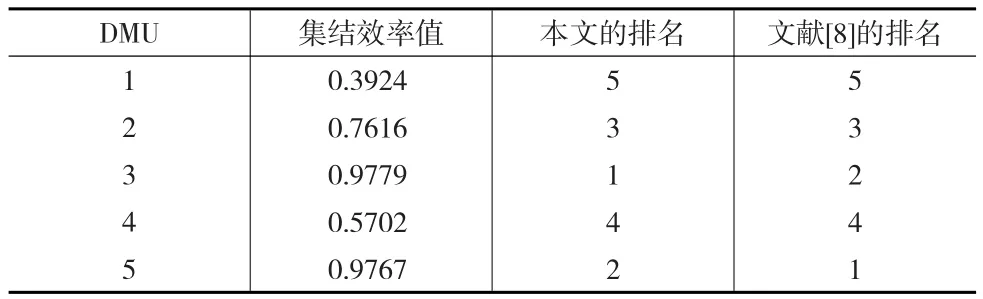
表4 效率分数及排名对比

本文得到的结果与文献[8]运用该算例得到的结果仅在DMU3和DMU5之间有差异，其原因可能是因为文献[8]是在传统CCR模型的基础上运用误差传递计算的，而本文是基于不同的交叉效率模型求解的，不仅考虑了自评效率并且考虑了他评效率分数，并且考虑了决策单元之间的竞争合作关系，由分组结果也可以看出DMU3与其他除DMU2以外的所有决策单元均是合作的关系，所以用本文的方法求得的DMU3的效率分数会稍高，排到了第一位。从本文的结果看，DMU3和DMU5在仁慈型模型和竞合交叉效率模型下不能充分排序的问题也得到了解决，该方法可以对5个决策单元进行充分的排序。

4 结论

本文在区间DEA交叉效率中引入邻域互信息，并提出区间值邻域互信息的计算方法，根据决策单元在投入产出之间的相关性对其进行分组，充分展示了邻域互信息在处理离散数据时的便捷性，以此对竞合交叉效率模型进行改进，然后利用潜在信息函数处理小样本数据的优势，将三个效率分数进行加权平均得到一个最终的效率分数。本文所提的方法解决了交叉效率选择策略不确定的难题，以及单一交叉效率模型排名不一致及排名不充分的问题。算例验证了所提方法的合理性，但是关于区间邻域互信息的距离计算方法和δ的确定有待进一步研究，且本文只是通过一个算例对所提方法进行了验证，对实际案例中投入产出区间范围较大时的可行性问题有待考证。