面向购物篮数据的稀有序列模式挖掘算法

周忠玉,皮德常

(南京航空航天大学 计算机科学与技术学院,南京 211106)

1 引 言

购物篮数据是指人们每天去超市购买食品,包括肉类、谷物、蔬菜、水果、牛奶、鸡蛋、酒类等日常生活用品的数据.这些数据能够真实地反映出人们的生活水平和生活质量.因此,挖掘此类数据对提高人类的生活水平和生活质量具有显著的意义.目前多数数据挖掘研究者偏好挖掘频繁的数据项,而忽视了稀有模式挖掘.以购物篮数据为例,为了提高商品的整体销售量,商家通常会将那些消费者经常一起购买的商品放在一起销售.因此,他们通常会对一批数据进行关联规则挖掘,找出频繁序列,摒弃非频繁的序列.然而,参照联合广告的互补性和非互补性,我们设想:既然两种毫无关联的广告产品放在一起会加深人们对两种品牌的认识,那么我们是否也可以将两种毫不相关的商品也放在一起销售,从而引起消费者对新品牌的注意,加深对老品牌的印象？这可能也是一种提高销售量的策略.如果假设成立,那就意味着我们不能像关联规则那样随意丢弃非频繁(稀有)的序列,相反要利用好这些非频繁的序列,找出它们的规律.为此很有必要对商品进行稀有序列模式挖掘的研究.

本文针对上述问题及假设,结合购物篮数据提出了一种稀有序列模式挖掘算法ISM-BD(Infrequent Sequence Mining of Shopping Basket Data).该算法通过挖掘稀有数据中的隐藏规律来进一步提高商品销售量.本文做出的主要贡献如下:

1)ISM-BD算法设置时间变量来限制序列项的时间,从而使挖掘结果具有时效性与可用性.

2)ISM-BD算法的提出充分利用了本该舍弃的非频繁数据.

3)提出综合权重因子,使得算法的挖掘结果更符合实际的区域差异性.

4)在ISM-BD算法的基础上,给出了一种异常值检测算法ISMO(Infrequent Sequence Mining based Outlier)来检测购物篮数据中的异常数值.

本文的组织结构如下:第2节介绍关于稀有的数据挖掘研究的相关工作;第3节对面向购物篮数据的稀有序列模式挖掘算法进行讨论分析并给出算法扩展;第4节使用公开的购物篮数据进行实验,验证本文提出的ISM-BD算法的正确性和有效性;第5节对全文做出概要性的总结并给出进一步的研究方向.

2 相关工作

2000年,Han提出的FreeSpan算法[2]是第一个涉及模式增长的算法.2001年,Pei Jian对FreeSpan算法做了改进,提出了PrefixSpan算法[3].同年,Zaki提出了SPADE算法[4],其算法的大体思想是利用等价类对全空间进行划分,从而得到一系列的子空间,以此来提高算法效率.2004年,Pei和Hant提出了Prefix算法[5].该算法摒弃了生成候选集的通用策略.因此,它的运行速度比一般的算法都要快.2016年,宋海涛等提出基于模式挖掘的用户行为异常检测算法[11].该算法通过比较挖掘出的频繁模式来检测用户行为的异常值.本文的扩展算法ISMO也是基于这种理念提出的,但本文采用的是稀有模式,而非频繁模式.同一年,为简化交易过程,提高网络交易的可靠性,王艳冰等提出FPM算法[12].该算法借助日志与频繁模式的一致性来保证挖掘结果的正确性.2017年,韩楠等提出FPNMine算法[13].该算法引入支持度技术矩阵,极大地提高了算法的挖掘效率.同年8月,吕存伟等提出EHUSN算法[14].该算法能够对非候选集序列进行快速剪枝,从而提高算法效率.同年9月,谢志轩等改进了HUM-UT算法,并提出IHUM-UT算法[15].该算法主要通过压缩原算法表头的大小来提高算法的时间效率.2018年,李维娜等提出一种新的频繁模式挖掘算法SG-FIP[16].该算法通过精简挖掘结果来提高挖掘精度.

至此,所有的关于序列挖掘的研究都是挖掘频繁序列的,并没有挖掘稀有序列.

2007年L.Szathmary提出了著名的Apriori-Rare算法[6].这是关于稀有序列挖掘的首篇文章.此后,许多稀有序列挖掘算法都是据此提出的.2011年S.Tsang提出了一种基于树结构的稀有模式挖掘算法RP-Tree[7].2012年L.Szathmary又提出了一种优化的Walky-G算法[8].2015年ARSPM算法[9]被提出.在此基础上又提出了一种更为高效的AMRSPM算法[9].同年,Sweetlin Hemalatha提出了一种基于异常值的稀有序列模式挖掘算法——MIP-DS[10],并进一步拓展为MIFPOD算法[1].2016年Ouyang在AMRSPM算法的基础上提出了基于大量事务的最小稀有模式挖掘算法——MRSP算法[10].其中以MIP-DS算法较为经典,该算法的思想大致如下:①生成1-序列;②通过计算1-序列的支持度判断生成1-稀有序列,并排序;③以1-稀有序列为基础生成候选序列;④计算候选序列的支持度,生成稀有最终的稀有序列.

本文在MIP-DS等算法的基础上,提出了ISM-BD算法.该算法修正了滑动窗口,使之与序列项的数量关联;引入了时间变量用于限制序列项的有效时间;采用综合权重因子作为衡量序列的区域差异性的标准.结合购物篮数据对算法进行了实验验证和分析.

3 稀有序列挖掘算法

本文提出了一种面向购物篮数据的稀有序列模式挖掘算法ISM-BD.该算法主要的思想大致如下:由原始序列生成1-序列;判断其时间限度是否在指定的范围内,以决定是否生成1-稀有序列;将1-稀有序列作为原始序列,生成候选序列;判断候选集的时效性和其支持度,生成最终的稀有序列.

3.1 基于综合权重因子的稀有序列挖掘

购物篮数据受许多因素影响,如工资水平、生活习性、地方习惯、甚至于自然灾害等因素.我们不可能要求经济发达地区同落后地区具有相同的购买力;也不可能将北方的面食消费量和稻米消费量放在一起比较.如果通过直接设定统一的阈值δ来判定某一序列项是否为稀有项,往往不具有通用性.例如可能存在如下情景:

情景1.设定某一区域h1的阈值δ= 0.3.理论上,只要Support(a)< 0.3,Support(b)< 0.3,序列项a和序列项b都被认为是稀有项.但实际上由于序列项a和序列项b的实际购买力不同,只有当Support(b)< 0.2时,序列项b才能被认为是稀有项.

情景2.设定区域h1和区域h2的阈值δ= 0.3.理论上,对于区域h1和区域h2来说只要Support(c)< 0.3,那么序列项c就被认为是稀有项.但实际上由于不同区域的饮食习性不同,对于h2地区来说只需要Support(c)< 0.4,序列c就应该被认定为是稀有项.

可见,设定统一的固定阈值δ不能满足挖掘结果准确性和通用性的需求.甚至会使得其挖掘结果是完全错误的.为此本文提出一种固有动态阈值σ的概念.固有是指在同一区域下,序列组的判定阈值是确定的.动态是指在不同区域下,序列组的判定阈值是不确定的.我们把同一区域下每个序列项对序列组的影响称为影响因子,用矩阵X表示:

其中xij表示在区域i下,第j个序列项的影响因子(i=1,2,…,m,j=1,2,…,n).

定义一组单映射fi,记作:

fi:xij→σi

其中σi为区域i对应的判定阈值;fi为区域i下的单映射关系,也可以将上述映射用公式(1)式表示:

σi=fi(xij)

(1)

将上述这种固有动态阈值称为综合权重因子,用符号σ表示.通过采用综合权重因子会使得挖掘结果更符合实际情况并且具有一致性和准确性.综合权重因子是衡量序列组的区域差异性度量.其值为影响某一序列组的各种因素权重的加权求和,用公式(2)表示:

(2)

其中hi为区域i对序列组的影响因素,称之为环境因子.由此可见不同区域的阈值是不同的.但是针对实际情况,只要阈值满足公式(3),它们的挖掘结果在稀有程度上是相当的.

(3)

其中,σmax是最大的综合权重因子,σmin是最小的综合权重因子,α为常数(0<α<0.5).

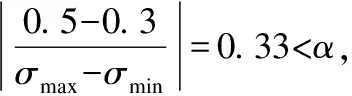
算法1.ISM-BD

Algorithm1.Infrequent Sequence Mining of Shopping Basket Data

Input:原始序列S,滑动窗口长度|SW|,环境因子hk,矩阵X,最小时间间隔minGap和最大时间间隔maxGap.

Output:稀有序列.

1.SC1←{1-sequence}

2.For each 1≤k≤m

3. For each 1≤l≤n

4.σk=∑hkxkl(xkl是矩阵X的元素)

5. End for

6. For every sequencei∈[minGap,maxGap]

10. End for

11. For every sequencei∈[minGap,maxGap] & & SiF1

12. SCnext←Candidate(i)

15. End for

16. iFk=iF1∪iFnext

17.End for

算法1说明:

步骤1.从原始序列S中找到所有长度为1的序列,放入集合SC1中.

步骤2.判断挖掘区域hk.计算区域hk下对应的综合权重因子σk.

步骤3-5.取出矩阵X中的k行元素,利用公式(2)计算综合权重因子σk.

步骤6.限定集合SC1中所有1-序列的时间间隔.若在有效时间内则进入步骤7-9.若不在有效期内则放弃该序列并返回步骤6判断下一个序列,直至所有1-序列判断完毕.

步骤7-10.分别计算SC1中所有1-序列的支持度并将其按照支持度升序排序,然后根据判断公式选出集合SC1中所有1-稀有序列并将它们放入集合iF1中.

步骤11.判断除了iF1中序列以外的所有剩余原始序列是否在限定的时间间隔内.若在有效时间内则进入步骤12-15.若不在有效期内则放弃该序列并返回步骤11判断下一个序列,直至所有序列判断完毕.

步骤12-15.在剩余序列中生成候选集,放入集合SCnext中.之后计算候选集中所有序列的支持度,根据判断公式选出所有剩余的稀有序列并将其放入集合iFnext中.

步骤16.合并集合iF1与集合iFnext形成区域hk下最终的稀有序列集iFk.若只有一种区域,则结束算法.否则返回步骤2.

3.2 基于异常值的算法扩展

在3.1节中研究的序列都是理想的序列,即不存在错误、空白、人为失误等异常因素.然而,在现实生活中这样的情况往往不会发生.因此,为了使算法更符合实际情况,我们把异常值考虑进去.

异常值是一种与大多数观测值大不相同的值[1].例如:在滑动窗口SW中有一序列s的属性与其他序列的属性大不相同,我们就把序列s称为滑动窗口SW中的异常值.

为了更加清楚的介绍基于异常值的稀有算法,我们引入异常值判断公式(4)至公式(6).首先给出序列权重因子(SWF).假设S = {s1,s2,s3,…,sn-1,sn}是滑动窗口SW中的n个序列,IF为所有稀有序列的集合.对于每一个序列s,它的SWF可以用公式(4)来计算.

(4)

显然,如果序列s中存在异常值,那么它会生成更多的稀有序列,即IF会增多.反之,如果序列s的SWF值越小,那么它越有可能存在异常值.

下面给出稀有序列误差因子(IDF).假设S = {s1,s2,s3,…,sn-1,sn}是滑动窗口SW中的n个序列,由公式(2)计算得出的综合权重因子为σ,对于每个稀有序列is,其IDF为:

(5)

显然,如果序列s的支持度小于综合权重因子为σ,那么它就是稀有序列.但是序列的异常程度是由序列s偏离综合权重因子σ的程度决定的.因此,对于基于异常值的稀有算法,IDF是必不可少的.

最后,给出基于异常值的稀有序列因子(IOF).对于每个序列s,它的IOF为:

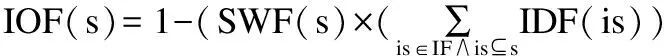
(6)

其中SWF是序列权重因子,IDF是稀有序列误差因子.基于异常值的扩展算法伪代码见算法2.

算法2.ISMO

Algorithm2.Infrequent Sequence Mining based Outlier

Input:原始序列S,稀有序列的长度|IF|,环境因子hk,矩阵X.

Output:异常序列集.

1.For each 1≤k≤m

2. For each 1≤l≤n

3.σk=∑hkxkl(xkl是矩阵X的元素)

4. End for

1Basket实验数据集公开地址： http://files.cnblogs.com/files/fengfenggirl/%E5%85%B3%E8%81%94%E8%A7%84%E5%88%99%E6%95%B0%E6%8D%AE.rar

5. IF←iFk// using IDMBDSB Algorithm

6. For every s ∈SW

7. S(s)=0 A(s)=0

8. For everyi∈IF

10. ifi⊆ s

11. S(s)+=1

12. A(s)+=IDF(i)

13. End if

14. End for

15. SWF(s)=S(s)÷|IF|

16. IOF(s)=1-(SWF(s)*A(s))

17. if (IOF(s)>σk)

18. output s

19. End if

20. End for

21.End for

算法2说明:

步骤1.判断挖掘区域hk.计算区域hk下对应的综合权重因子σk.

步骤2-4.取出矩阵X中的k行元素,利用公式(2)计算综合权重因子σk.

步骤5.将算法ISM-BD形成的稀有序列集iFk赋值给集合IF.

步骤8-14.利用公式(5)计算IF中所有稀有序列的稀有序列误差因子IDF值.

步骤15-16.分别利用公式(4)和公式(6)来计算稀有序列的序列权重因子SWF和稀有序列因子IOF.

步骤17-21.判断序列s的稀有序列因子IOF是否大于综合权重因子σk.若是,则输出;否则继续循环操作,直至不能产生新的异常序列为止.循环结束后,若只有hk则结束算法,否则返回步骤1.

4 实验结果及分析

实验设置2个不同的环境因子以作对比.其中h1=0.1,h2=0.5.实验的数据来源于公开的basket数据集1.

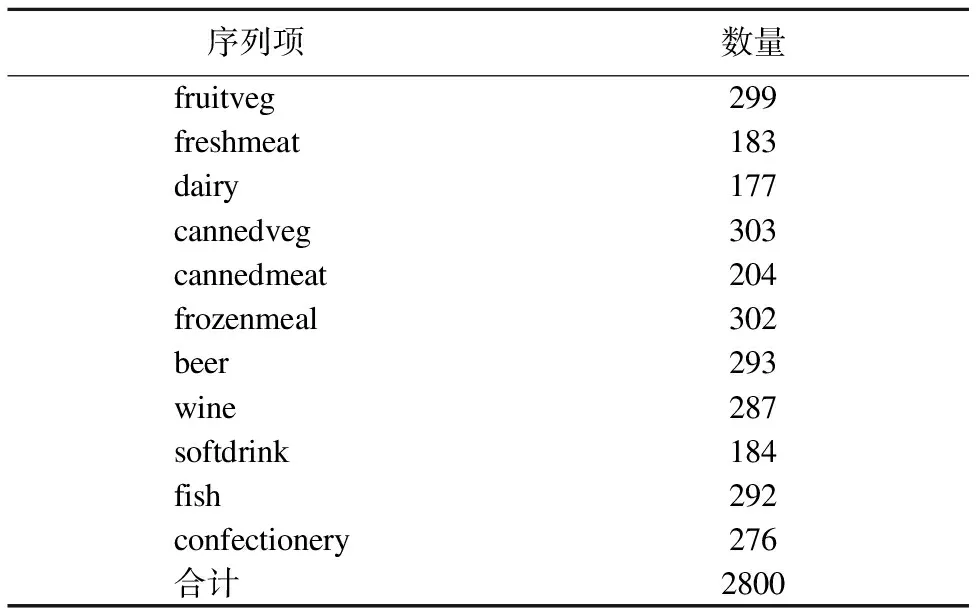
该数据集的商品总数有16469个,购物的商品序列项种类总共有11种,序列项个数总共有2800个.具体分布情况见表1.

实验采用的是同一批数据源(表1数据源)在区域h1和区域h2下挖掘稀有序列.由于区域差异性,不同区域内的各个序列项的影响因子可能不尽相同.为此,在不同区域h1和h2内,我们使用的各个序列项的影响因子分别为x1j和x2j(j=1,2,…,11).其具体数值如表2所示.

根据公式(2)计算得出综合权重因子σ1=0.2,σ2=0.265.ISM-BD算法在区域h1下对购物篮数据的挖掘结果如表3所示,在区域h2下对购物篮数据的挖掘结果如表4所示.

其中,表3和表4的第1列是结果,第2列是条件,第3列是支持度,第4列是置信度.例如:表3的第一行表示购买鲜肉的顾客就不会购买汽水.其支持度为4.2%,置信度为22.95%.通过表3可以发现使用ISM-BD算法在区域h1下可以挖掘出3个稀有模式.模式1:购买鲜肉(freshmeat)或奶制品(dairy)或两者都买的顾客不会购买汽水(softdrink);模式2:购买鲜肉或汽水或两者都买的顾客不会购买奶制品;模式3:购买奶制品或汽水或两者都买的顾客不会购买鲜肉.从这3种模式中,可以看出顾客不会同时购买鲜肉、汽水和奶制品.从它们的支持度可以看出上述3种食品两两购买的情况只占4.2%、3.3%和3.5%,3种食品全部都购买的情况则只占0.7%.可见,算法1挖掘出来的结果是正确的,它们都是不频繁(稀有)出现的序列.因此,在区域h1下,对于某新型品牌的奶制品,可以将其和鲜肉或汽水放在一起销售.这样做可引起顾客的注意,打响品牌知名度,从侧面提升销售量.从表4的第3列支持度同样可以看出ISM-BD算法在区域h2下的挖掘结果也为不频繁(稀有)序列.由此可见该算法在不同区域下都能很好的挖掘出稀有序列,算法是有效的.

表1 购物篮原始数据项分布
Table 1 Original data in the shopping basket distribution

序列项 数量fruitveg299freshmeat183dairy177cannedveg303cannedmeat204frozenmeal302beer293wine287softdrink184fish292confectionery276合计2800

表2 影响因子的值
Table 2 Value of the influencing factors

j值x1jx2j10.220.0520.140.0330.120.0340.220.0550.140.0460.220.0570.200.0580.200.0590.140.03100.200.05110.200.05

表3 区域h1下的挖掘结果
Table 3 Result of mining in region h1

综合权重因子σ1=0.2后项前项支持度 %置信度 %softdrinkfreshmeat4.2022.95dairy3.5019.77freshmeat dairy0.7021.21dairyfreshmeat3.3018.03softdrink3.5019.02freshmeat softdrink0.7016.67freshmeatsoftdrink4.2022.83dairy3.3018.64dairy softdrink0.7020.00

表4 区域h2下的挖掘结果
Table 4 Result of mining in region h2

综合权重因子σ2=0.265后项前项支持度 %置信度 %softdrinkfreshmeat4.2022.95dairy3.5019.77cannedmeat4.2020.59freshmeat dairy0.7021.21freshmeat cannedmeat1.3031.71dairy cannedmeat0.9029.03freshmeat dairy cannedmeat0.3042.86dairyfreshmeat3.3018.03softdrink3.5019.02cannedmeat3.1015.20freshmeat softdrink0.7016.67freshmeat cannedmeat0.7017.07softdrink cannedmeat0.9021.43freshmeat softdrink cannedmeat0.3023.08freshmeatcannedmeat4.1020.10softdrink4.2022.83dairy3.3018.64dairy softdrink0.7020.00dairy cannedmeat0.7022.58softdrink cannedmeat1.3030.95dairy softdrink cannedmeat0.3033.33cannedmeatfreshmeat4.1022.40dairy3.1017.51softdrink4.2022.83freshmeat dairy0.7021.21freshmeat softdrink1.3030.95dairy softdrink0.9025.71freshmeat dairy softdrink0.3042.86

对比表4和表3可以看出,在不同环境h1和h2下,即使数据源相同,但挖掘的结果却有很大的差异.例如:在环境h1下挖掘出了3种稀有模式,而在环境h2下挖掘出了4种稀有模式并且数目也完全不同.这就体现了综合权重因子的意义.它会挖掘出更加符合当地区域的稀有序列,也会使得挖掘结果更符合实际情况.

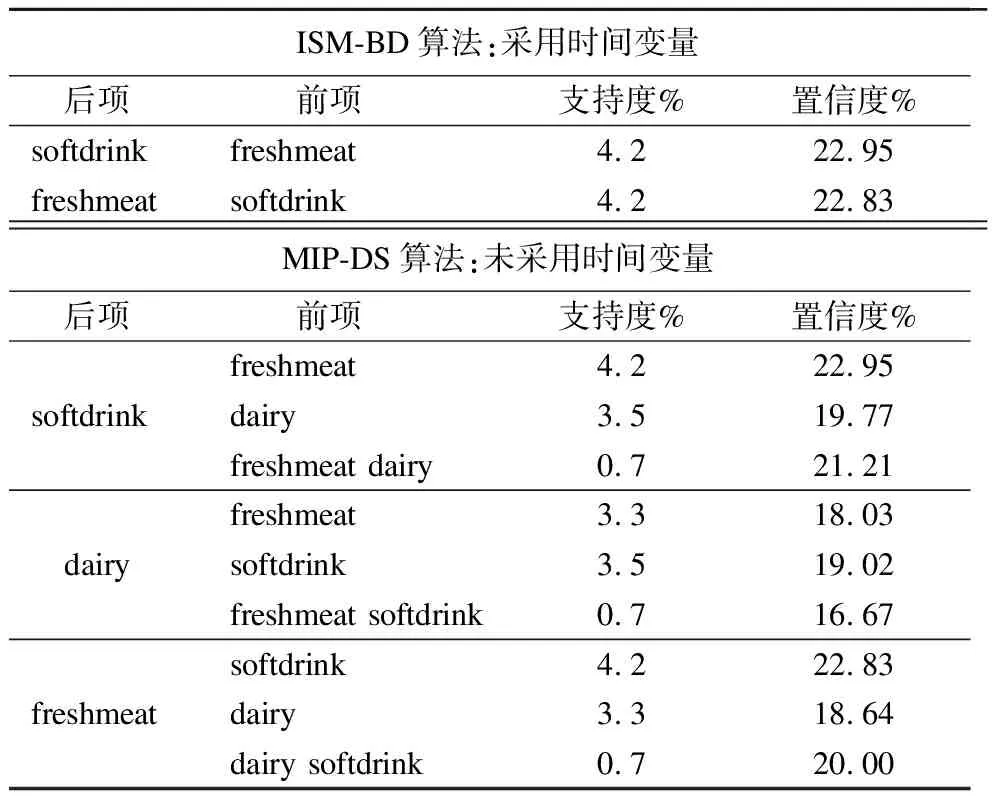
对数据源做进一步的处理,为其增加时间项.设置时间变量为minGap和maxGap.ISM-BD算法采用时间变量,MIP-DS算法未使用,而阈值等其他条件相同.表5给出了两种算法挖掘结果对比.

从表5可以看出dairy项不在[minGap,maxGap]内,不具时效性.ISM-BD算法采用时间变量,其挖掘结果比没有采用时间变量的MIP-DS算法简单有效.它仅包含具有时效性的稀有序列模式.以后项汽水(softdrink)为例,ISM-BD算法只包含一条稀有序列,当顾客购买鲜肉(freshmeat)后不会购买汽水;MIP-DS算法包含三条稀有序列,当顾客购买鲜肉或奶制品(dairy)或两者都购买的时不会购买汽水.ISM-BD算法的挖掘结果都在时效内,都是有效的稀有序列;MIP-DS算法的9条挖掘结果中仅有2条在时效内,其余均为无效序列.所以,ISM-BD算法的挖掘结果具有非常高的有效性.

表5 采用时间变量前后的算法结果对比
Table 5 Comparison of the results of the algorithm before and after using time variable

ISM-BD算法:采用时间变量 后项 前项支持度%置信度%softdrinkfreshmeat4.222.95freshmeatsoftdrink4.222.83MIP-DS算法:未采用时间变量 后项 前项支持度%置信度%freshmeat4.222.95softdrinkdairy3.519.77freshmeat dairy0.721.21freshmeat3.318.03 dairysoftdrink3.519.02freshmeat softdrink0.716.67softdrink4.222.83freshmeatdairy3.318.64 dairy softdrink0.720.00

5 结 论

本文针对频繁序列模式挖掘对非频繁项不加以利用而普遍舍弃以及挖掘结果存在时效性和区域差异性的问题.提出了基于综合权重因子的稀有序列模式挖掘算法.该算法能够很好的利用稀有序列,挖掘出它们的规律.既能够从侧面提高商品的销售量,又能够符合实际区域环境.采用公开数据验证了算法的有效性.今后还要采用更多大量的数据来改进实验以求得更为准确的结果.也可以对算法2做出进一步的改进,提高其效率.