粒计算思维下的BP神经网络在金融趋势预测中的应用

沈泽君,杨文元,2

1(闽南师范大学 福建省粒计算及其应用重点实验室,福建 漳州 363000) 2(闽南师范大学 数据科学与智能应用福建省高等学校重点实验室,福建 漳州 363000)

1 引 言

BP(Back Propagation)神经网络是一种模拟人脑神经网络结构从而具有一定预测功能的数学模型,由于具有较强的自学习能力、自适应能力以及容错能力等优点,使它成为一种比较适合金融趋势预测的方法[1,2].BP算法主要由两部分构成,信号的正向传播和误差的反向传播,其结构主要由输入层、若干层隐含层、输出层三部分组成[3].正向传播就是输入信号经输入层到隐含层进行的非线性变换,并产生和输出信号.若输出信号与期望输出不相符,则转入误差的反向传播过程.反向传播的过程就是将误差通过隐含层向输入层逐层反向传递,将其分解到各层,各隐含层以此作为调整权值与阈值的依据.经过反复的训练学习,以目标的负梯度方向对参数进行调整,最终确定与最小误差相对应的网络参数[4].

BP神经网络在对非线性预测中有很强的适应能力[1,5].目前基于BP神经网络在金融趋势预测上的研究主要是通过调整BP网络的相关参数来提高预测精准度[6-9].金融趋势的周期性变化多端,不同周期对预测结果的影响不一,而传统的BP神经网络对其预测是基于单个周期的,没有很好地考虑不同周期走势下的相互影响[10,11].BP神经网络能够较好的模拟人脑神经,在金融趋势预测上具有较强的适应能力.但是由于金融趋势会受到多因素的影响,并且影响不一,传统的BP神经网络是基于单周期粒度,其预测模型与人脑思维还是有所不同.

金融趋势的不同周期从粒计算的角度来解释,就是数据集中的不同粒度.粒计算是当前人工智能研究领域中模拟人类思维和解决复杂问题的新方法[12].粒计算的基本组成主要包括粒子、粒层和粒结构.粒子是一个较为模糊的统称,它是构成粒计算模型的最基本元素,例如本文的实验对象股票收盘价,当天的收盘价就是一个小粒子,一周的收盘价就是一个较大的粒子.粒层这个概念的提出就是为了区分这些颗粒,粒层就是在处理某项问题时,对处理对象进行一定的划分,这个划分可以看成是对处理对象进行了一个分类[13].对于现实中人脑对金融趋势的预测,会根据不同粒度的不同作用进行一个综合的考量,其考量的过程在传统的BP神经网络中较难体现[14].

本文提出的粒计算思维的BP神经网络(Back Propagation on Granular Computing,BPGC)弥补了传统BP神经网络这方面的不足.BPGC算法先通过对数据集进行预处理,即对数据集进行不同粒度的划分,构造粒度矩阵;然后根据不同的粒度矩阵进行BP训练得出各粒度的不同影响力,即各粒度的权值;最后对各粒度下的预测结果进行加权平均,得出最终的预测结果.BPGC能够较好的模拟人脑在对金融趋势预测时不同粒度相互影响的过程,在综合考量不同粒度影响力时加入了权值的方法,比人脑的经验评判更具逻辑性.

在浦发银行股票收盘价数据集上进行实验,根据2017年全年的数据进行模型训练,依次预测2018年前10天的收盘价数据.实验结果表明,BPGC算法在金融趋势预测上优于传统的BP神经网络算法,具有较高的精准度.

2 相关工作

2.1 BP神经网络及归一化改进

BP算法利用输出结果与真实结果的误差来估计输出层的前一层误差,再用这层误差来估计更前一层的误差[15],如此反复获取各层的误差估计,其具体的BP神经网络结构图如图1所示.

图1 BP神经网络结构图Fig.1 Structure graph of BP neural network

其中,X=(x1,x2,…,xn)T是输入向量;O1是实际输出值;Y=(y1,y2,…,ym)T和P=(p1,p2,…,pt)T是隐含层输出;V=(v1,v2,…,vm)T和W=(w1,w2,…,wl)T是第一隐含层和第二隐含层的权值矩阵.

BP神经网络算法的信号由正向传播和反向传播两阶段构成.

BP神经网络的具体算法描述如下:

1)正向传播阶段

①输入层输入:x1～xn.

②第一层隐含层输出:

(1)

其中Vmn为第一层隐含层权值,θm为节点阈值.

③第二层隐含层输出:

(2)

其中wlm为第二层隐含层权值,θl为节点阈值.

④输出层输出:

(3)

2)反向传播阶段

沿着误差函数相反的梯度方向修改权值,使得网络模型收敛[4],输出层的权值修改ΔTtl为:

(4)

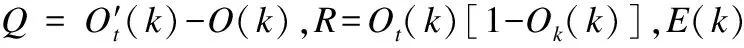
由此可得修改后的输出层权值为:

Til(k+1)=Til(k)-ηΔTil,

(5)

其中η为经验步长.

同理可求得第一层隐含层的权值修改ΔVmn和第二层隐含层的权值修改ΔWlm.

由此可得修改后的第一层隐含层权值为:

ΔVmn(k+1)=Vmn(k)-ηΔVmn,

(6)

其中η为其经验步长.

第二层隐含层权值为:

ΔWlm(k+1)=Wlm(k)-ηΔWlm,

(7)

其中η为其经验步长.

由于金融趋势数据在一定时间范围内会着落在一个数值区域[16].所以在预测前要对数据采取归一化处理,通过控制数据集的着落范围来提高BP运算效率.归一化的计算式为:

(8)

其中xmax和xmin分别是数据集X的最大值和最小值,xn为输入值,xp为归一化后的输出结果.

2.2 粒计算思维下的粒度概念

设K=(U,R)是一个数据集,p∈R是U上的一个等价关系,其中U/P={z1,z2,…,zn}.P的粒度记为GD(P),其具体的计算式为:

(9)

P的粒度表示其分辨能力[13,17],对∀u,v∈U,当(u,v)∈P时,u、v在P下不可分辨,属于P的同一个等价类;若不可分辨,则属于不同的p-等价类.由此可得,GD(p)表示在U中随机挑选的两个对象的P-不可分辨的可能性的大小,其值越大表示分辨能力越弱[12,18,19].

3 粒计算思维下的BP神经网络

3.1 粒度矩阵构造及预处理

人脑在对金融趋势进行预测时,会多方面考虑不同周期的数据走势情况,例如会对日线、周线、月线甚至是季度、年度走势进行综合考虑,然后才能较为精准的预测下一天的走势[20].对此,需要构造一个粒度矩阵,方便BP算法对其运算,其构造步骤如下:

①选取数据集x1至xn的一维矩阵,记为S,其中S的长度为LS.

②构造k行,Ls-k列的k粒度构造过渡矩阵H,H矩阵的第n行数据为:H(n,n:LS)=S(1,1:LS-n-1).

③取k粒度构造过渡矩阵H的部分矩阵为构造完毕矩阵Hk,其Hk的取值过程为:Hk(1:k,1:LS-k+1)=H(1:k,k-1:LS).

其构造过程如图2所示.

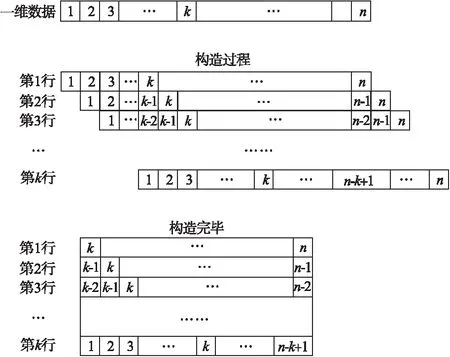
图2 数据集粒度矩阵构造过程Fig.2 Process of constructing granularity matrix

其中一维数据中的k表示xk,n表示xn;构造完毕后的第一行数据为xk至xn,最后一行数据为x1至xn-k+1,第一列数据为(xk,xk-1, …,x1)T.

为提高运算效率,对粒度矩阵不可直接利用BP神经网络进行运算,需根据公式(8)进行归一化预处理.得到的各粒度下的归一化矩阵记为Hpk,图3表示的是k粒度下的归一化矩阵Hpk.

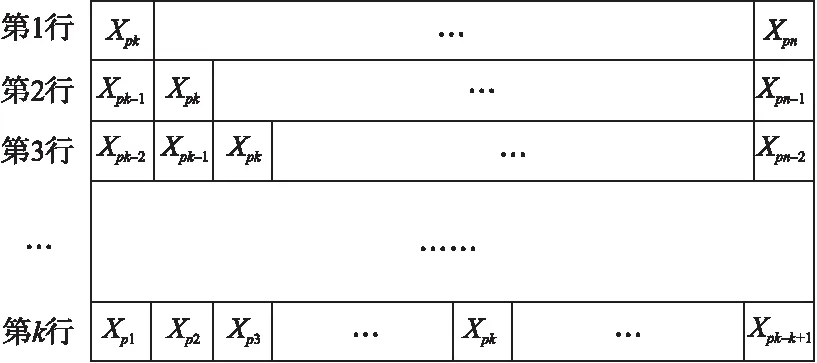
图3 k粒度下归一化矩阵HpkFig.3 Normalized matrix Hpk under k granularity

归一化后的粒度矩阵Hpk的数值均在-1到1之间.在对其进行BP训练时,把某列作为输入,输出结果与下一列第一个数据进行学习比对.如第一列(xpk,xpk-1, …,xp1)T作为输入时,则与第二列的xpk+1进行学习比对.然后反方向传播误差,各层根据误差对参数进行相应的调整,调整后再对输入数据进行正向传播.以此类推,当误差达到设定范围内,得出一个训练模型.

3.2 预测值误差及权值处理

根据不同粒度下的数据样本划分,经过BP神经网络的运算,得到的预测值是不同的.根据人脑对于金融趋势的预测经验,要预测出一个较为精准的预测结果,需要对多粒度下的预测结果进行综合考虑,对此BPGC算法须对各粒度下的预测数值进行加权.而各粒度的权值与其预测误差有关,误差计算式为公式(10),其中di表示第i天的真实值.

(10)

各粒度下第i天的预测值与真实值的误差值为Err(oi),但为了便于比较该粒度下对其预测的误差率,需要用误差均方差δ来表示,其计算式为公式(11).其中n表示的是所预测的总天数.

(11)

记各个粒度下的误差均方差为δk、各粒度下的精准度为Acck,其对应关系为公式(12).记各粒度下的权值为fk,其计算式为:

Acck=1-δk,

(12)

(13)

其中Δf为误差乘数.

(14)

3.3 BPGC算法模型

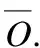
图4 BPGC算法模型Fig.4 Model of BPGC

BPGC算法具体步骤如下:

算法.粒计算思维的BP神经网络(BPGC)输入:一维的金融趋势历史数据集X=(x1,x2,…, xn,…,xm)T.输出:加权预测值O.1)从数据集X中选择前n个数据进行粒度矩阵构造,并进行归一化预处理,得到矩阵Hpk.2)对各粒度归一化矩阵Hpk进行BP训练,并得出预测值On+1-m.3)根据公式(10)～(13)计算各个粒度下的权值fk.4)对所有粒度下的预测值Ok使用权值fk用公式(14)进行加权计算,得出O.

4 实验与结果分析

在这部分,将通过实验来验证本文提出的BPGC算法在金融趋势上的有效性.本文采用从中国财经网下载的浦发银行(股票代码:600000)2017年全年收盘价的数据进行学习建模并得出各粒度下的权值,依次预测出2018年前10天的数据进行预测比较.

4.1 实验设置

根据浦发银行股票的走势特征以及实验预测结果的误差比较,选取了周期天数为2天至59天的58个粒度,其中粒度1对应的周期天数为2,粒度2对应的周期天数为3,以此类推,粒度58对应的周期天数为59.因为周期为1天的单个收盘价数据在BP神经网络预测下一天数据效果差,周期天数从60天开始,其预测数值误差较大,所以没有纳入BPGC的粒度选取中.

根据多次实验,对BP神经网络的相关参数设置详见表1.其中由于BPGC是对其各粒度下的预测值进行加权平均,所以设置输出数为1;输入个数与各粒度有关,粒度周期为10天则输入层k=10;由于浦发银行的股票收盘价均小于18元且精确到分,考量历史数据走势,对其误差均方差设置为0.000001.

表1 BP神经网络参数值
Table 1 Parameter values of BP neural network

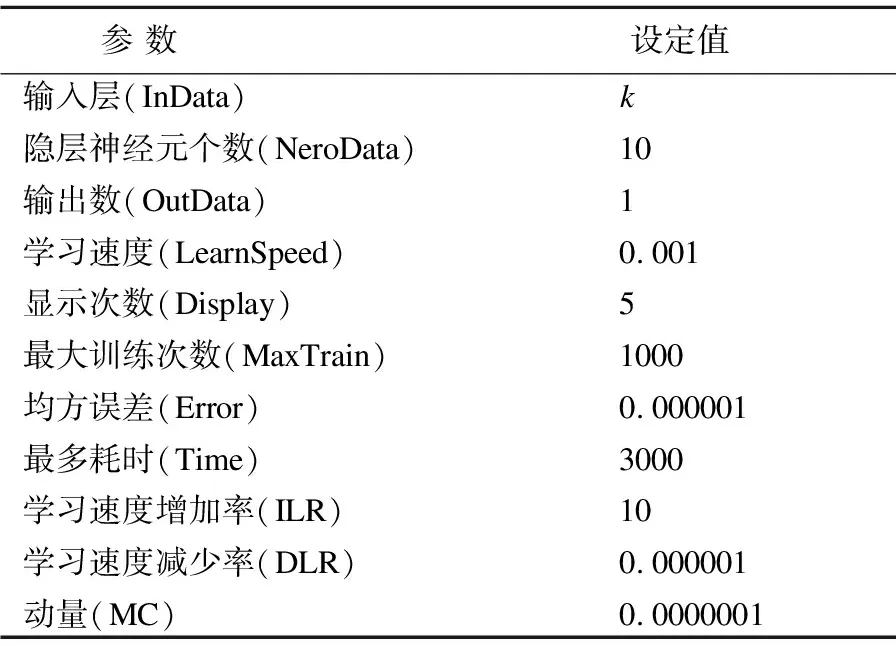
参 数设定值输入层(InData)隐层神经元个数(NeroData)输出数(OutData)学习速度(LearnSpeed)显示次数(Display)最大训练次数(MaxTrain)均方误差(Error)最多耗时(Time)学习速度增加率(ILR)学习速度减少率(DLR)动量(MC)k1010.001510000.0000013000100.0000010.0000001

4.2 实验结果分析

进行预实验得出各粒度的权值:把2017年最后10天的数据作为测试集,剩余数据作为训练集;根据训练集数据学习出模型,然后依次预测2017年最后10天的预测值,最后根据误差值来计算各粒度的权值.图5是各粒度下误差值的三维图,其中X轴表示的是预实验中第n天实验,Y轴表示的是粒度,Z轴表示的是误差值,其误差越接近于零表示性能越好.

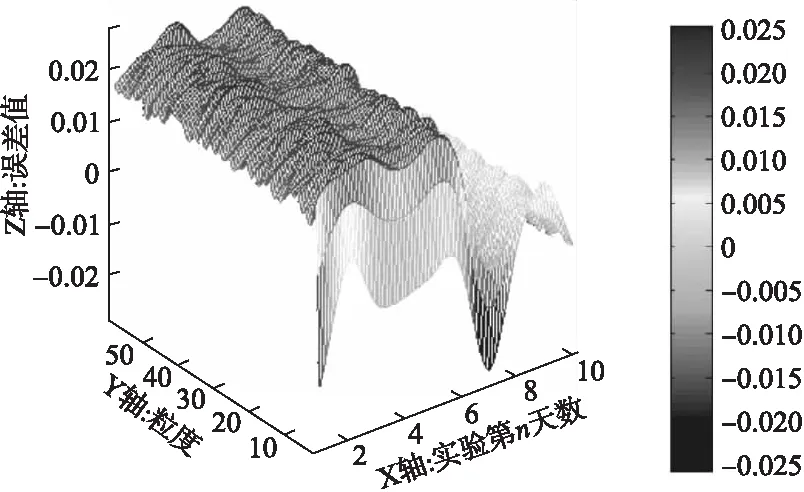
图5 各粒度下误差值三维图Fig.5 Error value at each granularity

如图5所示,各粒度在前5天前的预测结果误差较大,且预测结果普遍偏高.粒度10至粒度58的预测误差均有大于0.02的情况.综合来看,预测结果普遍大于真实值,权值计算中的误差乘数Δf应小于1.

根据预实验得到的误差均方差值通过公式(12)、公式(13)可得到各粒度下的权值.其中,误差乘数Δf根据各粒度误差值的特性,设置为0.99.各粒度下的权值如图6所示,其中X轴表示粒度,Y轴表示各粒度的权值.

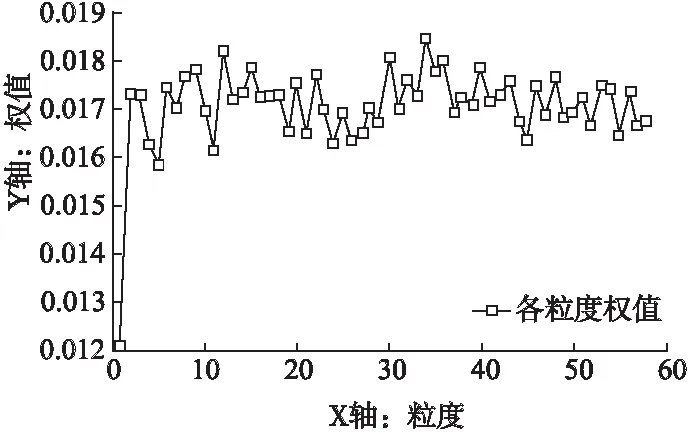
图6 各粒度权值图Fig.6 Weights of each granularity

如图6所示,粒度1的权值最小,粒度34的权值最大.粒度5、粒度11的权值较小,粒度6至粒度58的权值主要分布在0.016～0.018之间.其分布结合图5各粒度下误差值的走势来看,粒度1的误差值偏大,所以权值最小;粒度6以后的误差值分布较为集中,相对其权值分布较为均衡;粒度5、粒度11在实验的第6天以后误差较大,对其权值有一定影响.

根据预实验得出的权值,运用BPGC算法对浦发银行2017年全年的收盘价数据进行学习建模,并依次预测2018年前10天的收盘价.其预测结果与传统BP神经网络预测值的误差比较图如图7所示,其中X轴表示预测的天数,Y轴表示预测值的误差,曲线越靠近0其效果越佳.

如图7所示,BPGC在预测的前6天中具有较高的精准度,后4天中的精准度不如传统的BP算法.其原因是由于误差乘数Δf设置为0.99.根据图5所示,前5天中的误差普遍较高,Δf设置小于1有利于降噪,提高精准.但是由于后5天的误差值较前5天普遍较低,Δf=0.99的设置会起到一定的反作用,从而提高了误差.

图7 BPGC、传统BP预测值误差比较图Fig.7 Comparison between BPGC and traditional BP on prediction error

为了便于分析BPGC在实验中的效果,引入BPGC预测结果与各粒度下的预测结果对比图.其中X轴表示预测天数,Y轴表示各个粒度的数值(其中刻度0表示真实值、刻度1表示BPGC的预测值、刻度2至59表示粒度1至粒度58的预测值),Z轴表示预测结果的数值.图中黑色标线为BPGC的预测数值走势.该图的预测数据走势与真实值走势越靠拢表示预测效果越佳.

图8 真实值、BPGC与各粒度预测值结果比较图Fig.8 Comparison of real value,BPGC and the predicted results of each granularity

如图8所示,BPGC的预测结果与真实值比较,在前6天的预测中,其预测值优于各个粒度的预测结果,但是在预测的第7～10天中,与各个粒度比较,其误差的优越性较低.其原因主要有二:一是Δf的设置对于后面几天的预测比较不适用;二是第6-10天的数据波动较大,与前几天的实际数据比较来看,有呈现突然上升的趋势.综上所述,BPGC在金融趋势波动较小的情况下具有较高的预测精准,其Δf的设置可以进一步划分区间或者针对预测趋势的涨幅度进行分类设置.

5 总 结

本文提出了粒计算思维下的BP神经网络(BPGC)并将其应用于金融趋势预测.BPGC算法解决了传统BP算法对金融趋势周期考虑不足的问题,能够较好的模拟人脑对金融趋势的判断过程,通过考量各粒度的不同影响力,对各粒度的预测结果按不同权值进行调整.实验表明,BPGC算法比传统的BP神经网络在金融趋势预测上更具优越性.但是还存在以下不足:一是Δf的取值不能普遍应用于所有情况;二是BPGC算法对幅度变化较大的趋势预测精准度较低.在今后的工作中,将着力解决Δf取值与由于变化幅度大导致精准降低的问题.