基于聚类的多维数据热点发现算法
2019-03-13聂晓辉
邹 磊,朱 晶,聂晓辉,苏 亚,裴 丹,孙 宇
1(清华大学 计算机系,北京 100084) 2(北京小桔科技(滴滴出行)有限公司,北京 100193)
1 引 言
随着大数据概念的普及,人们逐渐认识到了海量数据中存在的巨大价值.各种针对大数据的数据挖掘研究和成果也如雨后春笋般涌现,热点发现就是被广泛研究的数据挖掘问题之一[1-3,18,19].热点发现有助于快速地初步了解整体数据的特点,并为后续的分析工作提供方向与决策基础.通过热点发现能够从网民产生的海量文本内容中挖掘出当前网民讨论的热点话题,例如反腐,某明星结婚等,以及这些话题的热度[3].通过热点发现还能够快速发现用户数据的明显特征,例如用户通常在白天使用某项服务,以及大部分用户都使用苹果手机等.本文针对多维数据的热点发现进行研究.
多维数据通常包含多个与目标事件相关的特征,这些特征可以是用户的手机品牌、使用的服务类型、事件发生的时间、用户的地理位置、用户的网络延迟、软件版本、服务器负载、用户年龄等,每次目标事件发生都对应一条多维数据.例如图 1所示,该多维数据包含5个特征,并且展示了7条数据作为示例.特征可以根据其取值特点分成数值型特征和类别型特征.数值型特征的取值是存在一维欧式距离关系的数值,例如图 1中的网络延迟和时间.类别型特征的取值被分成多个类别,例如图 1中的手机品牌,网络类型,所在城市.
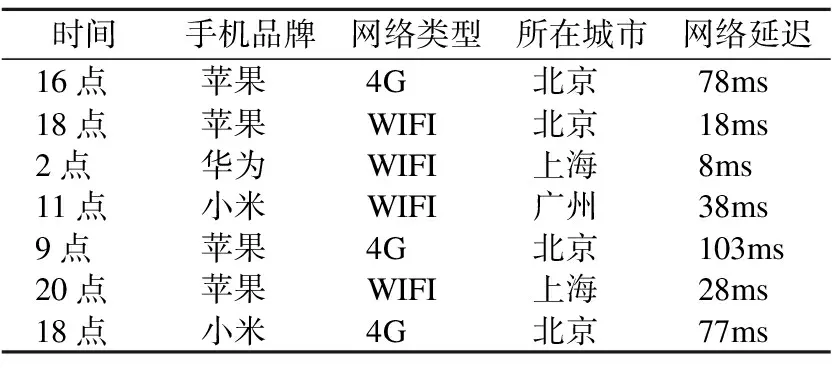
图1 多维数据示例
Fig.1 Example of multi-dimensional and multi-class data
如果把多维数据的每一个特征都看作一个维度,那么多维数据就是分布于由各个特征的取值范围构成的特征空间中的数据.例如图 2所示,在由时间、网络延迟和所在城市三个特征构成的特征空间中,每个黑色方格都是一条数据,白色方格表示该处没有数据.多维数据的热点发现希望能够找出图中数据集中的两个热点区域(图中的虚线处),并以特征取值组合[17]{时间∈[18,24],所在城市∈[北京,深圳,上海],网络延迟<30ms}和{时间∈[6,9]}将这两个热点区域的信息呈现给数据分析人员,特征取值组合通过限定一个或者多个特征的取值范围来表示数据的取值范围.实际的特征空间通常会超过三维,但是受限于图片的表达能力,在这里仅以三维特征空间作为例子.这些热点信息有助于进行定向推荐、优惠卷精准发放、针对性优化产品性能、以及广告定向投放等.
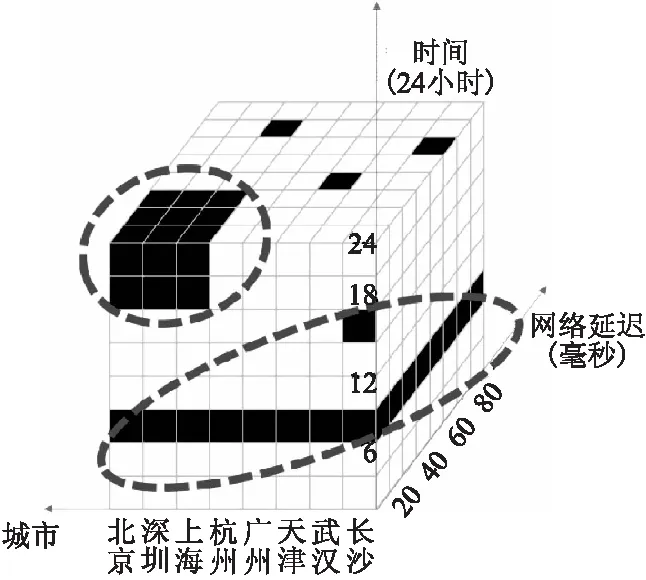
图2 多维数据聚集区域示例Fig.2 Example of data area with high density
近年来,有非常多的热点分析研究成果发表.[1]利用MapReduce加速K-means的计算,设计了ASQHTD算法,用于从航空领域的大量文档中发掘航空公司服务品质热点.该文首先对文本进行特征提取,提取出仅含有数值型特征的高维文本向量,然后用ASQHTD作用于这些文本向量找到航空品质热点.[2]基于MFIHC聚类和TOPSIS针对短小的微博数据设计了实时热点发现算法,该文在对文本特征进行聚类时引入了知网的主义库进行语义的相似度计算.[3]基于LDA设计了OLDA模型,用于对网民的评论进行热点发现.但是这些算法或者是基于相关的领域专业知识对原始数据进行特征提取之后得到只含有一种类型特征的多维数据(即只有数值型特征或者只有类别型特征)[1],或者根据相关的领域专业知识为数据设计距离或者相似度计算方法[2],这些算法都无法直接用于解决多维数据的热点发现问题.
通常热点发现问题都通过聚类方法解决[1-3],本文也使用聚类方法来解决多维数据热点发现问题.根据多维数据热点发现的需求,本文选择了聚类算法CLTree[4]作为基线算法.CLTree通过往目标数据中均匀地填充一类虚拟数据来构造双类别数据,再用决策树对数据进行分类,分类完成后将虚拟数据移除,分类结果就成了聚类结果.
本文对CLTree[4]进行如下重要改进,设计了CLTree+来解决数据热点发现问题:
1)增加了对类别型特征聚类支持.CLTree在对类别型特征进行聚类时,必须先根据一定的规则将类别型数据转换成数值型数据,而CLTree+可以直接处理类别型特征,提升了聚类效果和算法的适用性.
2)提升了对存在周期性特性的数值型特征进行聚类的效果.存在周期性特性的数值型特征包括几点,周几等.CLTree+根据特征的周期性提出了新的聚类方法,相比于CLTree直接将存在周期性的特征当成数值型特征处理,CLTree+可以得到更好的聚类效果.下文中用周期型特征指代含有周期性特性的数值型特征,数值型特征均指代不含有周期性特性的数值型特征.
3)CLTree+对计算速度进行了优化.CLTree会先将数据分裂成尽可能小的子集,再对这些子集进行聚类,当数据量非常大时,这种方法的计算时间开销非常大.CLTree+引入了剪枝策略,使数据分裂到符合要求即停止,使计算效率提升了O(n)倍.
CLTree+被应用于某大型互联网公司的业务数据,得到了很好的效果,成功地找出了若干符合专家经验的数据热点.
2 研究目标
热点定义:热点是指特征空间中的数据区域Area,其数据密度D>=Dthr,并且数据量Q>=Qthr.Dthr和Qthr为常数阈值,其取值根据具体应用由专家根据相关领域的专业知识选取.
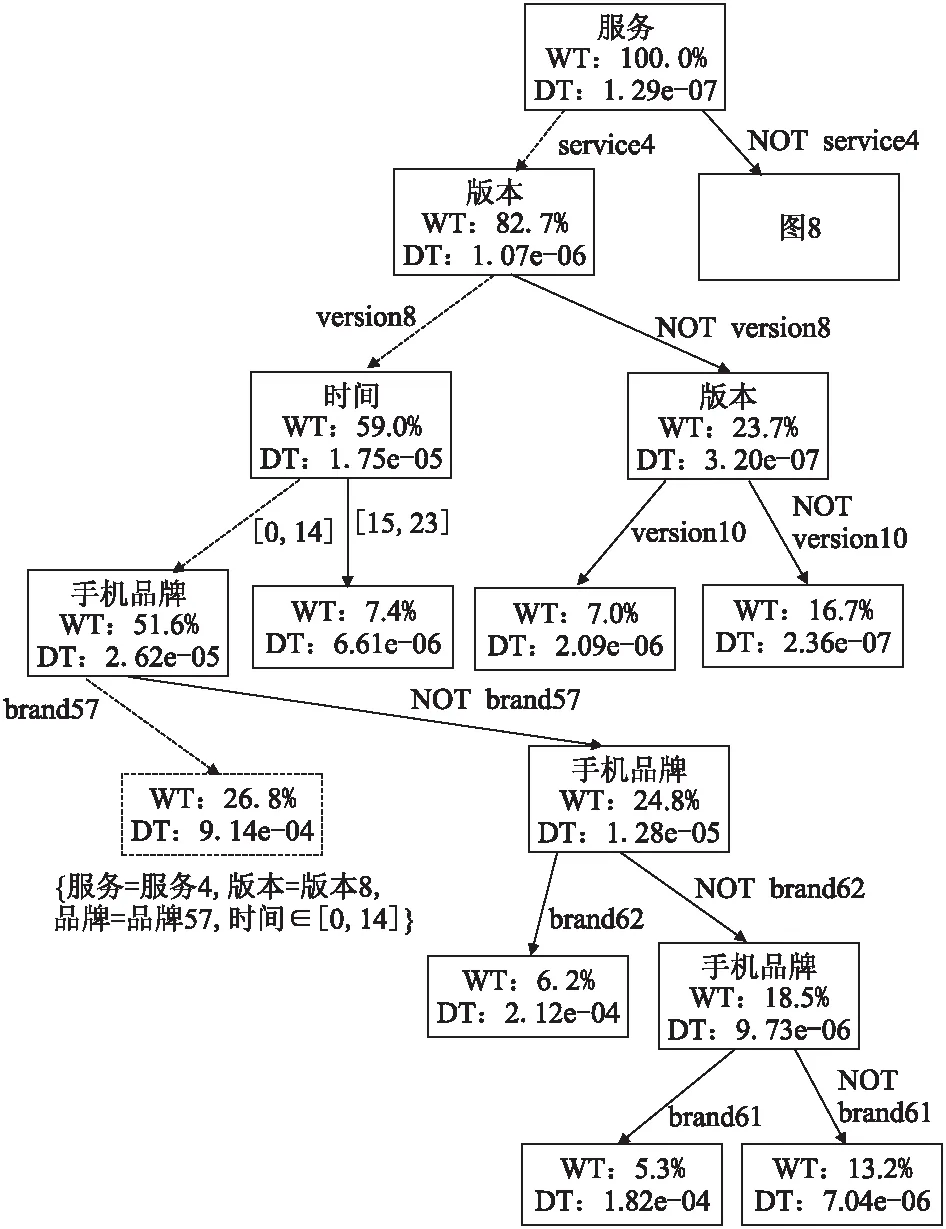
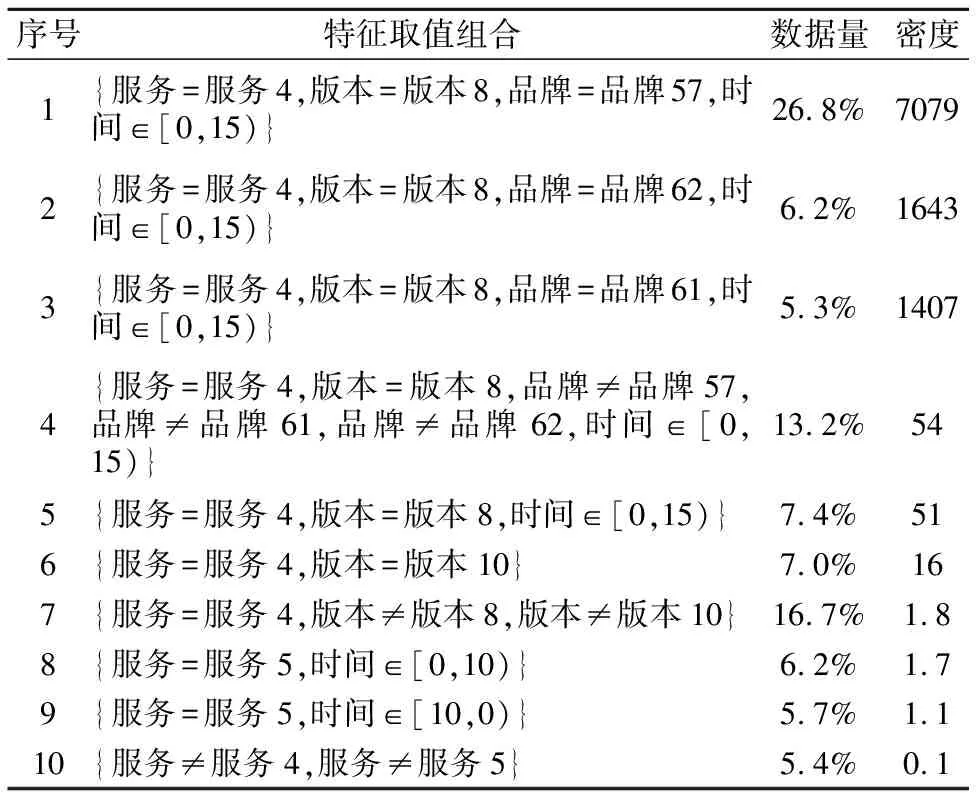
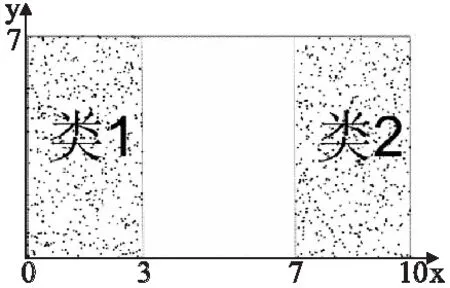
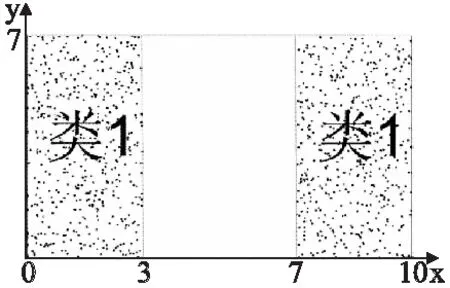
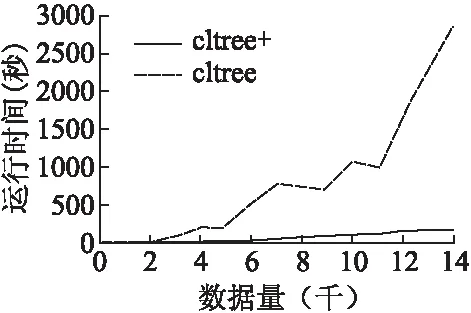
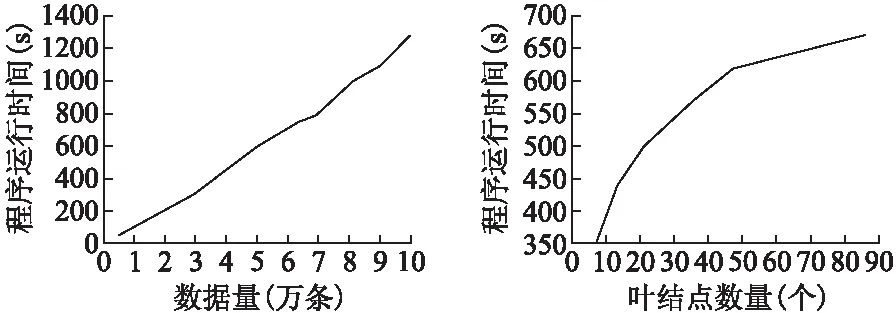
热点的表示:热点用特征取值组合表示.周期型特征的取值范围采用[16]中的表示方式,表示为[a,b)、[a,b]、(a,b)或者(a,b],其中以[a,b)为例说明其含义,用P表示该特征的周期,0≤a,b (1) 数据密度定义:用于描述特征取值组合的数据集中程度的数据密度D的计算方式为 (2) 其中#data为该特征取值组合覆盖的数据数量;Li为该特征取值组合所确定的区域中特征i的长度. 连续数值型特征取值范围可表示为(a,b]、[a,b]、(a,b)、[a,b)离散数值型特征取值范围表示为,其长度为 L=b-a (3) 连续周期型特征取值范围可表示为(a,b]、[a,b]、(a,b)、[a,b),离散周期型特征取值范围表示为[a,b),P为该特征的周期,其长度为 (4) 取值范围为集合{v1,v2,…,vn}的类别型特征的长度为 L=mod({v1,v2,…,vn}) (5) 如果某个特征没有出现在特征取值组合中,这意味着对这个特征没有限制,那么该特征的取值范围为整体数据中该特征的取值范围,在计算该特征取值组合的数据密度时也需要除以该特征的长度.例如,对于图 1中的数据,特征取值组合{时间∈[20点,4点),网络类型=4G,所在城市≠北京}的各个特征的长度分别如表 1所示,周期型特征时间的取值范围为20点至4点,4点先加上一个周期24小时再减去20点得到长度为8;手机品牌的取值范围没有限制,该特征所有可能的不同取值有3种;网络类型限定为4G,该特征长度为1;网络延迟的取值范围也没有限制,该特征长度为其最大取值103ms减去8ms.不同的特征其长度的物理意义不同. 对于同一份数据集的不同特征取值组合,可以用它们的数据密度来对比不同特征取值组合下的相对数据疏密程度.但是数据密度无法用于对比不同数据集下的特征取值组合的数据疏密程度,因为不同的数据集的特征集不同,其特征长度的物理意义不同. 表1 特征长度计算方法示例Table 1 Example of calculating feature′s length 本文针对多维数据进行热点发现的具体目标是要找出一些满足以下条件的特征取值组合: 1)特征取值组合的数量越少越好.根据奥卡姆剃刀原则[14],特征取值组合的数量越少,数据分析人员越易于理解. 2)每个特征取值组合下的数据都比较密集.特征取值组合的数据密集程度通过数据密度与整体数据的数据密度的比值来评价. 3)每个特征取值组合包含的数据量都较大.特征取值组合表现出的数据特点的显著程度与数据量呈正相关,如果数据量太少,那么这个特征取值组合表现出的特点不显著,因此并不是热点. 4)各个特征取值组合之间必须没有数据重叠,例如{服务类型=快车&&用户设备=苹果}与{用户设备=苹果}这两个特征取值组合中间就存在数据的重叠,它们都包含了满足条件{服务类型=快车&&用户设备=苹果}的数据.找出的这些特征取值组合是呈现给数据分析人员进行后续的人工分析的,各个特征取值组合之间没有重叠可以使这些特征取值组合的意义更加直观. 然而前三个诉求其实是矛盾的,为了覆盖尽可能多的数据通常会导致特征取值组合的平均数据密度的下降,最极端的例子就是整体数据构成一个特征取值组合时,虽然数据覆盖量为100%,但是只要数据不是均匀分布地,就肯定能找到数据密度更高的特征取值组合.特征取值组合数量越少与它们的的平均数据密度越大这两个诉求也是相悖的,因为只要一个热点内的数据不是平均分布的,就总是能够在其中找到数据密度更大的特征取值组合.不同数据对这三个诉求的侧重点也不同,因此很难对热点发现的结果设定一个最优的评价标准.数据分析人员需要根据自己的实际需要,通过调整算法的输入参数叶结点最小数据量和最小信息熵增益来权衡这三个诉求. 本文使用聚类方法来解决多维数据的热点发现问题.例如图 3中的二维数据所示,其中的黑色点就是业务数据,数据集中分布在两片区域A和B中,区域C的数据则非常的稀疏.根据前面提到的需求,理想的情况是能够找出表示A和B两个区域的特征取值组合.为了实现这个目标,首先对数据进行聚类,在数据被聚成A,B和C三个类之后,再用刚好能够覆盖类中所有数据的特征取值的组合来界定每个类的边界.描述类A和类B边界的特征取值组合就是多维数据热点发现希望找到的结果. 聚类问题是一个已经被研究了非常久的基础机器学习问题,有非常多的聚类算法已经被设计出来并成功地运用到不同的场景[5-12].但是多维数据热点发现问题对聚类算法的要求非常多,首先数据分析人员可能并不知道数据应该被聚成多少类,其次聚类结果的边界越整齐越好,从而能够轻易地表示为特征取值的组合,除此之外,多维数据中既有类别型特征,又有数值型特征,聚类算法需要能够处理这两类特征.而各个聚类算法都有自己的应用限制,很少有聚类算法能够完美地满足上述所有要求.例如常用的K-means算法需要输入聚类数作为参数,同时K-means聚类得到的不同类之间的边界通常是不规则的,并且为了用特征取值组合描述类,同时各个特征取值组合之间没有重叠,需要对聚类的结果进行复杂的调整.因此在选择聚类算法时还需要对所有聚类算法进行仔细挑选.根据多维数据热点发现的需求和各种聚类算法的优缺点,CLTree最终被选择作为解决多维数据热点发现的基线算法. 图3 热点发现算法基本思路示意图Fig.3 Basic idea of hotspot detection alogrithm CLTree的聚类结果的边界整齐,可以直接用特征的取值组合进行表示,并且不需要预先输入需要将数据分成多少类,CLTree会根据数据的特点决定聚类结果中类的数目,因此本文选择CLTree作为基线算法.但是CLTree仅支持处理数值型特征、处理具有周期性的数值型特征效果不好,并且计算效率低.本文创新设计的CLTree+算法有效解决了CLTree的上述缺点. 图4 多维数据热点发现算法流程图Fig.4 Flowchart of multi-dimen-sional data hotspot detection algorithm 算法的基本流程如图 4所示. 在使用CLTree+为数据进行聚类以及计算数据密度时都需要确定整体数据的取值范围.数值型特征的取值范围为其取值的最小值与最大值之间的范围,即[vmin,vmax].周期型特征的取值范围为一个周期P的范围,即[0,P).类别型特征的取值范围为整体数据的取值集合{v1,v2,…,vn}. CLTree+相对于CLTree进行了如下三点改进. 3.5.1 通过剪枝提升算法的计算效率 CLTree首先将数据分裂成尽可能小的子集,直到每个子集中只包含最多两条数据或者该子集中的所有数据都相同为止,然后再根据算法的两个输入参数类最小数据量和相邻类最小相对密度差将相邻的子集进行合并.这种将数据先分裂成更小子集再合并子集的方法实际上是多此一举,并且在实际使用过程中这种作法的时间开销太大,当数据量非常大的时候,这种开销用户是无法承受的.同时这种方法会导致原本还可以进一步分裂的子集最终被划分成一个类,因为CLTree分裂数据的逻辑是在满足最大信息增益的前提下看该次分裂成的子集是否满足类最小数据量.假如子集A根据CLTree算法的最佳分裂规则会被分裂成B和C两个子集,但是子集B中的数据量小于类最小数据量,那么在CLTree最终的合并过程中B和C又会被合并成A,A将作为最终聚类结果的一个类.但是实际上A还可能被分裂成D和E子集,D和E的数据量都大于类最小数据量,只是A分裂成D和E的信息增益要小于A分裂成B和C.CLTree+在数据分裂时会首先根据类最小数据量筛选候选分裂点,再根据最大信息增益在这些候选分裂点中选择最佳的分裂点,如果最佳的分裂点得到的信息增益小于最小信息增益,则该子数据集停止分裂.本文根据该规则修改CLTree为数值型特征寻找最佳分裂点的evaluateCut(D)算法[4]为evaluateCutPlus(D)算法,并用evalueateCutPlus(D)算法来为数值型特征选择该特征上的最佳分裂点. 3.5.2 类别型特征上的最佳分裂点选择 对于类别型特征,选择one-against-others[15]二分裂形成候选分裂点,而不选择穷举二分裂方式[14]形成分裂候选点.这么做是出于两个方面的考虑,第一点是为了加快决策树的计算速度.对于一个含有n种不同取值的离散型特征,所有可能的二分裂方式有2^n种,而one-against-others二分裂只有n种分裂方式.第二点是为了使分裂结果更易于为人所直观的理解.在类别型特征的维度上,取值不同的数据之间并没有固有的距离关系,因此仅能确定特征取值相同的数据应该被聚为一类,不存在像数值型特征那样的分裂边界插入数据聚集区域[4]的情况.对于类别型特征直接根据信息熵增益选择最佳分裂点.该算法如下: 算法1.类别型特征最佳分裂点选取 输入:待聚类的数据集data,待选取最佳分裂点的特征F,叶结点最小数据量minlen,最小信息增益minentro 输出:特征F上的最佳分裂点split 1)根据F的取值对数据进行去重得到F的无重复取值集合{vi,i=1,2,…,n} 2)split = None 3)for viin {v1,v2,…,vn}: 4) spliti= 将data分裂成datal和datar的分裂点 5) datal={vjif vj==vifor vjin data} 6) datar={vjif vj!=vifor vjin data} 7) if len(data1) 8) continue 9) split=(split与spliti中信息熵增益更大的一个) 10)返回split 3.5.3 周期型特征上的最佳分裂点选择 对于周期型特征,不能简单地将其当成数值型特征进行处理.虽然数据之间也天然存在着欧式距离的关系,但是由于该特征的周期性,在计算两个取值不同的数据点在该维度上的距离时有两种不同的计算方式,以一天的24小时举个例子,在没有确定日期的情况下,1点和2点之间可以说隔了1个小时,也可以说是隔了23个小时,因为今天的2点与明天的1点之间隔了23个小时.如果把周期型数据的取值范围看做一个圆,那么在圆上只找一个切分点是无法将圆分成两段的,需要两个切分点才行.[16]在使用决策树处理周期型特征时,选取两个切分点将周期型数据分成两段,从而构成一个分裂候选点.然而CLTree+不能直接根据信息熵增益从这种方法生成的分裂候选点中选择最佳分裂点,因为会存在分裂点插入聚类中间的情况.处理周期型特征时,首先假设周期型数据的取值都在0至周期P的范围内,如果数据的取值不在0至P的范围内,那么其取值可以通过加减P的整数倍映射到该范围内,周期型数据加减周期的整数倍其取值都是等价的.CLTree+每次在该取值范围内选取一个数值vi作为数据的最小边界,其它的数据的取值v按如下规则进行映射之后得到数据集Di. (6) 然后再用evaluateCutPlus(D)为该特征寻找一个最佳分裂点.CLTree+会依次遍历该特征在0-P上的所有取值作为数据的最小边界分别寻找一个最佳分裂点,这些最佳分裂点中信息熵增益最大的分裂点即为该特征上的最佳分裂点. 算法2.周期型特征最佳分裂点选取 输入:待聚类的数据集data,待选取最佳分裂点的特征F,特征F的周期P,叶结点最小数据量minlen,最小信息增益minentro 输出:特征F上的最佳分裂点 1)将特征F的数值映射到一个周期的范围内,并根据特征F的数值对数据进行排序以及去重得到无重复的升序序列{vi,i=1,2,…,n} 2)split=None 3)for viin {v1,v2,…,vn}: 4) datai={vjif vj>=vielse vj+P for vjin data} 5) spliti=evaluateCutPlus(datai) 6) split=(split与spliti中信息熵增益更大的一个) 7)返回split 如果数据集最终在所有特征中选择某一个周期型特征的最佳分裂点作为整个数据集的最佳分裂点进行分裂,且该分裂点是将数据映射成Di后得到的,那么在切分得到的子数据集中,数据会一直保持映射成Di,无需再重新进行映射. CLTree+是沿着数据的整齐边界分裂数据的,因此CLTree+的聚类结果能够天然地用特征取值的组合来表示.从根结点到该叶结点的分裂路径即一系列特征取值条件的组合就可以表示该类. 本文以整体数据的密度Dglob作为基准线,并为所有类计算其数据密度与Dglob的比值.CLTree+的聚类结果中数据密度大于Dglob的类即可视作热点.用户在实际使用该算法时可以根据实际情况选择密度最大的若干个类作为数据热点. 对于只包含数值型特征,数值型特征分裂时采用{取值<=v}和{取值>v}二分裂以及{取值>=v}和{取值 因为CLTree仅支持处理数值型特征,因此在对比CLTree+和CLTree的时间复杂度时,仅考虑CLTree+处理数值型特征的情况.因为CLTree+会根据叶结点最小数据量提前结束决策树分裂,因此CLTree+的结点数量不是O(n),而是O(1/k),其中k为叶结点最小数据量与总数据量n的比值,取值通常为常数.构建CLTree+的时间复杂度为O(mn3).CLTree的时间复杂度是CLTree+的O(n)倍. 对于类别型特征,CLTree+采用one-against-others二分裂,只需要遍历O(n)个分裂点,并且不需要对数据进行排序,处理每个特征时只需要遍历一次数据.只包含类别型特征的CLTree+的时间复杂度为O(mn). 对于周期型特征,CLTree+将其转换成数值型特征进行处理,相当于多了n倍特征,只包含周期型特征的CLTree+的时间复杂度为O(mn4). 对于含有mnum个数值型特征,mcat个类别型特征,mper个周期型特征的数据,CLTree+的时间复杂度为: O(mcatn+mnumn3+mpern4) (7) CLTree+的时间复杂度受所处理数据的特征类型影响非常大,处理周期型特征需要花费的时间最长,处理类别型特征需要花费的时间最短. 本次实验使用的业务数据为国内一家移动出行公司的订单数据,该数据为2017年中某一周内全国的业务数据.每一个用户使用一次该公司的服务就会产生一条业务数据,为了保护该公司的商业信息,以及考虑到实验程序与硬件的计算能力,实际被使用的数据量已经经过了采样,采样之后的数据量为10万条.每条业务数据都包含了7个特征,各个特征的信息如表 2所示. 所有实验数据都进行了脱敏,时间特征的取值加入了一定小时数的时间偏移,其它类别型特征的取值都用编号代替. 将CLTree+应用到实验数据后得到如图 5所示的聚类树,为了使图片更加清晰,部分内容放到图 6中显示.算法输入参数叶结点最小数据量定为总数据量的5%,最小信息熵增益定为0.01.图 5记录了数据分裂的详细过程,图中每一个结点都表示数据分裂过程中的一个数据子集,最上层的根结点表示整体数据集.如果一个结点有子结点,则说明该数据集继续进行了分裂.结点中的特征名表示该数据集在该特征上根据一定的条件进行分裂,而连接结点的边上的信息表示分裂该数据集的条件.例如,根结点表示的数据根据服务的取值被分成两个子数据集,一个子数据集中数据的服务特征取值均为服务4,另外一个子数据集中数据的服务特征取值均为非服务4.从根结点到目标结点的路径上的一系列分裂条件就构成了表示目标结点的特征取值组合,例如图 5中的结点(虚线框)所示,从根结点到该结点的4个虚线箭头表示的分裂条件就构成了表示该结点的特征取值组合{服务=服务4,版本=版本8,品牌=品牌57,时间∈[0,15)}.所有的叶子节点构成了最终的聚类结果. 表2 特征信息Table 2 Feature information 图5 移动出行公司订单数据建立的CLTree+(部分1)Fig.5 Result of CLTree+ clustering(Part 1) 表3按数据密度与整体数据的数据密度比值降序的方式展示了聚类结果中所有的类.最后的聚类结果中能够出现较多的像类1这样的数据覆盖量大且数据密度较高的类是比较好的结果,数据量大意味着根据该类进行决策的收益更大,数据密度大意味着根据该类进行决策时付出相同的成本能够获得更大的收益.但是通常子数据集会继续分裂出密度更大的子数据集,得到如类2和类3这样的数据量接近叶结点最小数据量的类.有时也会得到类4这样的类,其数据覆盖量远大于叶结点最小数据量,但数据密度远低于数据密度最大的几个类.这种类没有继续分裂得到数据密度更大的类是因为这个类的数据分布已经比较均匀,或者虽然能够分裂出一些数据密度非常大的子类,但是这样的子类的数据覆盖量小于叶结点最小数据量.因此针对特定的数据使用该算法时,需要根据具体的需求仔细的挑选叶结点最小数据量和最小信息熵增益这两个参数.对于一些数据密度非常低的类,如类10,并不是算法要找的热点,是可以忽略的类,数据分析人员可以根据自己的需求选择排序靠前的几个类作为热点. 图6 移动出行公司订单数据建立的CLTree+(部分2)Fig.6 Result of CLTree+clustering(Part 2) 表3 订单数据聚类结果类信息Table 3 Clusters information of CLTree+ clustering result 图5还能够给出数据在单维度上分布的信息.因为决策树会优先选择区分度最大的特征对数据进行分裂,因此越接近根结点的分裂特征,对数据的区分度越大,即在这些特征上数据分布得越不均匀.从图 5中可以发现数据首先根据服务进行分裂,而通过数据集在服务特征上的单维度分布可以发现82.7%的订单都是使用的服务4,还有11.9%的订单都是使用的服务5,使用这两种服务的订单占了所的订单的94.6%. 并没有一个通用的指标可以用于评价多维数据热点发现的结果,并且由于所有可能的特征取值组合数量巨大,因此也无法通过遍历并对比所有可能的特征取值组合来评价热点发现结果.目前主要依赖该移动出行公司的数据专家结合具体的专业知识对结果进行评估.通过对聚类结果的认真评估,数据专家一致认为热点发现的结果非常符合他们的历史经验,结果比较理想. 图7 x被当成数值型特征时CLTree的聚类结果Fig.7 Clustering result of CLTree when x is treated as numerical feature 实验数据为在{0≤x≤3或7≤x≤10,0≤y≤7}范围内随机生成的二维数据.用CLTree对该数据进行聚类得到如图7所示的两个类{0≤x≤3,0≤y≤7}和{7≤x≤10,0≤y≤7}.而用CLTree+对该数据进行聚类并将x轴的数据当作周期为10的周期型数据时图7中的两个类会被处理为一个类{x∈[7,3],0≤8≤7},如图8所示. 图8 x被当成周期型特征时CLTree+的聚类结果Fig.8 Clustering result of CLTree+ when x is treated as periodical feature 用于测试实验程序运行速度的硬件环境为一台搭载英特尔至强E5-2620,2.4GHz,64GB内存的服务器,操作系统为Debian 8.7,所使用的编程语言为Python2.7.实验程序为一个单机版单线程程序,并没有使用任何集群技术或者多线程技术. 5.5.1 CLTree与CLTree+的性能对比 本文使用CLTree与CLTree+处理相同的仅含有数值型特征的数据,得到的性能差异如图 9所示.在数据量相同的情况下,CLTree的运行时间远高于CLTree+. 图9 CLTree和CLTree+的性能对比Fig.9 Performance compa-rison of CLTree and CLTree+ 5.5.2 CLTree+性能 下面给出了将CLTree+应用于某大型互联网公司的业务数据时得到的数据量、每条数据包含的特征、CLTree+的分裂深度对程序速度的影响.所有程序运行速度的数据都是运行5次程序取平均值得到的.图 10展示了数据量对程序运行速度的影响,从图中可以看出程序的运行时间随着数据量的增加基本上是呈线性增长,这是因为实验数据中的特征除了时间以外全部为类别型特征.图 11展示了决策树分裂深度对程序速度的影响.从图中可以看出程序的运行时间随着叶结点数量的增加而增加,但是增长得越来越慢,基本呈对数曲线关系.出现这种情况是因为随着数据的分裂,子数据集中的数据量会越来越少.表 4展示了分别移除各个特征之后对程序运行速度的影响,表中的数据按照被移除特征的不同取值数量按升序排列,可以发现被移除特征的不同取值数量越多,程序减少的计算时间越多,对于相同类型的特征,不同取值的数量越多,所需要的计算量越大.客户端版本与下单时间的不同取值数量差不多,但是移除下单时间后程序减少的运行时间更长,这是因为下单时间是周期型特征,处理周期型特征更耗时. 图10 数据量对程序运行速度的影响Fig.10 Influence of data size on programme′s running speed图11 决策树分裂深度对程序速度的影响Fig.11 Influence of CLTree′s depth on programme′s running speed 表4 特征对程序运行速度的影响Table 4 Influence of feature′s character on programme′s running speed 本文用聚类方法解决了多维数据的热点发现问题,并详细介绍了如何根据多维数据热点发现的目标设计的聚类算法CLTree+来解决该问题,以及详细地介绍了为了实现热点发现的目标而对基线算法CLTree进行的改进.CLTree+可以直接处理类别型特征,处理周期型特征时效果也比CLTree更好.除此之外,CLTree+的计算效率远优于CLTree.本文设计的热点发现算法提供两个参数用于控制找出的热点的粗细粒度,方便算法使用者根据自己分析的数据的具体情况进行调整.从实验结果来看,算法成功的找出了数据聚集的区域,实验结果满足了预期的目标.下一步的工作将主要集中在使用并行化技术提高程序的运行效率,包括单机多线程并行和集群多机器并行.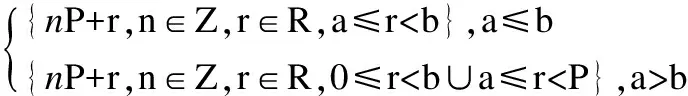


3 多维数据热点发现算法介绍
3.1 基本思想
3.2 聚类算法选择

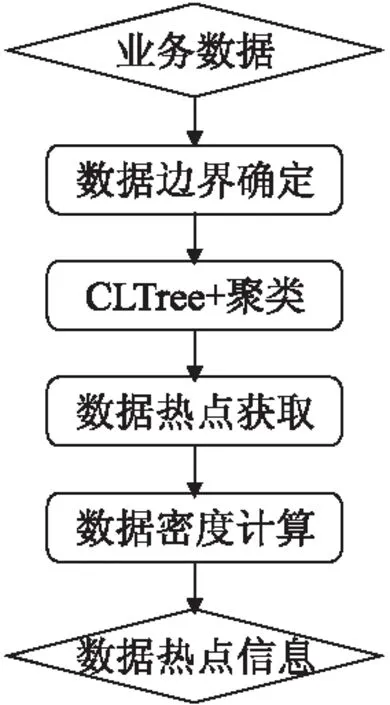
3.3 算法流程
3.4 数据边界确定
3.5 CLTree+
3.6 数据热点获取
4 算法时间复杂度分析
4.1 CLTree的时间复杂度分析
4.2 CLTree+的时间复杂度分析
5 实验与结果分析
5.1 实验数据介绍
5.2 实验结果介绍


5.3 效果评估
5.4 CLTree与CLTree+处理周期型数据效果对比
5.5 性能评估


6 结束语
