比较模型下ACS的快速精确诊断算法

陈 芳，梁家荣，张 乾

(广西大学 计算机与电子信息学院，南宁 530004)

1 研究背景

蚁群系统是通过对自然界中蚂蚁觅食行为的分析而提出的.蚂蚁之间通过信息素来进行相互联系[1]，即蚂蚁在寻找食物的过程中会产生一种信息素，它的同伴会根据其信息素的多少来选择路径.如果蚂蚁没有产生足够多的信息素，随着时间的流逝，信息素会消失，那么最初蚂蚁的觅食路径也会不复存在[2].反之，如果有许多蚂蚁选择同一条路径，那么这条路径的信息素会增加，从而会驱使更多的蚂蚁选择这条路径，也就是说，信息素最多的路径就是蚂蚁觅食的最短路径[3].

为了保证系统的可靠性，Preparata et al.提出了第一个系统级可诊断模型(PMC模型)[4].基于PMC模型，Maeng和Malek提出了比较模型(也称MM模型)，即借助于图论的思想，用无向图G(V，E)表示多重处理机系统，其中，V表示系统中的结点(处理机)集合，E表示结点(处理机)之间的连通关系，用结点vk比较结点va和vb，当且仅当结点va，vb，vk满足，(va，vk)∈E且(vb，vk)∈E，由此得到的测试结果用ω(vk：va，vb)来表示[5].表1展示了比较模型下结点的比较规则.基于MM模型，Sengupta和Dahbura提出了特殊化的MM模型(MM*模型)，即只要结点是相邻的，那么任意一个结点就需要去测试另外两个结点[6].

随着信息技术的快速发展，传统的故障诊断方法，不能够诊断出大量的故障处理机，且不能有效的将故障处理机替换为无故障的处理机.对于如何高效地解决多重处理机系统在运行过程中的故障诊断问题，学者们相继提出新的策略.而蚁群系统作为一个比较新颖的概念，逐渐受到学者们的广泛关注，与早期的启发式算法，如：遗传算法、模拟退火算法相比较，蚁群算法具有时间复杂度小，且易于在计算机上实现的优点.已有的关于ACS的研究囊括了基于蚁群系统的路由算法[7，8]以及在人工智能方面的应用[9]等,但关于蚁群系统的故障诊断分析，现还没有相应的研究成果，故本文通过模拟蚁群获取食物的过程，并对其最短路径进行分析，结合ACS环分割的方法，从而提出一种在比较模型下蚁群系统的精确诊断算法.

2 蚁群系统(ACS)中蚂蚁的觅食算法

定义1.在ACS中，把蚂蚁看做结点，蚂蚁之间形成的觅食路径看做结点之间的连接.

表1 比较模型下三个结点的比较规则Table 1 Rules of three nodes under the comparison model

定义2.用α表示信息素，蚂蚁vi走过路径a，蚂蚁vj走过路径b，假设从巢穴出发的蚂蚁vk是无故障的.如果α(a)>α(b)，且ω(vk：vi，vj)=1，那么ω(vi)=0(vi无故障),ω(vj)=1(vj故障)(见图1，灰色表示故障结点，白色表示无故障结点).

在图1中，蚂蚁vi，vj反馈给蚂蚁vk的信息为1，即路径a,b中的信息素有差异.蚂蚁vk通过反馈回的信息判断出蚂蚁vi是无故障的(蚂蚁vj是故障的)，也就是说蚂蚁vk到蚂蚁vi所处的觅食点是最短路径(蚂蚁vk到蚂蚁vj所处的觅食点不是最短路径)，因此蚂蚁vk可依据反馈回的信息选择最短觅食路径.

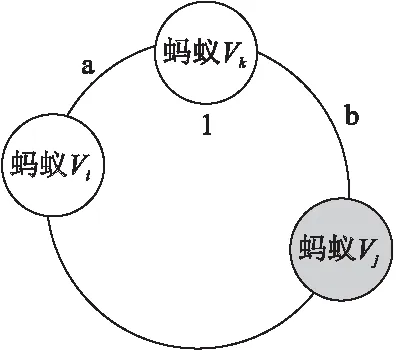
图1 蚂蚁觅食路径的分析图Fig.1 Analysis diagram of ant foraging path

依据以上蚂蚁觅食路径的理论，得到蚁群系统(ACS)中蚂蚁的觅食算法，如下：

算法1.ACS中蚂蚁的觅食算法

第1步.将参数αij,Δαij,M,N,a,b进行初始化.其中，αij表示信息素的强度，Δαij表示信息素强度的变化量，M表示蚂蚁的数量，N表示结点的个数，a,b表示常量.

第2步.对常量a,b进行迭代.

第3步.输入M(1～N)，启动蚂蚁计数器.

第4步.i表示蚂蚁的巢穴，j表示觅食点.

计算从i到j的可能路径.基于从结点i到结点j的所有可能路径(蚂蚁觅食过程)的状态转换规则，得到公式，如下：

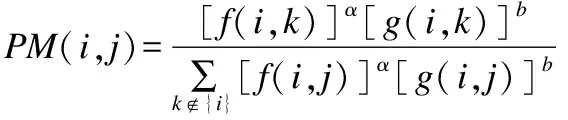
其中，PM(i,j)表示蚂蚁从i到j的行走概率，f(i,j)表示蚂蚁从i到j之间的信息素，g(i,j)表示蚂蚁从i到j的选择意愿.

第5步.根据测试的数据，比较PM(i,j)的大小，从而获得蚂蚁的初始觅食路径.

第6步.完成觅食路径的蚂蚁返回到巢穴.

如果Yes(都返回)，进行下一步，反之，跳到第4步.

第7步.算法结束.

通过算法1得到蚂蚁觅食的初始路径，第4节中，通过改变蚂蚁M的数量，对算法1进行多次仿真实验，随着蚂蚁数量的不断增多，蚂蚁的觅食路径逐渐趋近环.下面一节，将运用ACS环分割方法，对蚂蚁的觅食路径进行分析.

3 ACS的快速精确诊断算法

3.1 ACS环分割算法

定义3.蚂蚁从起始结点a到终结点b，途中经过所有其他结点且只经过一次，此路径组成的回路就是ACS环.

接下来的部分将得出一些关于ACS环在比较模型下的重要属性，这对于研究环分割算法是很有必要的.

引理1.一个ACS环由n个结点组成，其中有t个故障结点，如果n≥3t+1，那么存在这样的一个结点va，使得ω(va:va-1,va+1)=0.

证明：因为在系统中最多有t个故障结点且至少由3t+1个结点构成，那么一定存在三个连续的无故障结点va,vb,vc满足ω(vb:va,vc)=0.

由算法1，得到蚂蚁觅食的路径.将蚂蚁的觅食路径形成的环通过ACS环分割算法(见算法2)得到一系列的序列，并对其进行分析研究.

算法2.ACS环分割算法

第1步.找到一个测试结果为0的蚂蚁(结点)，且其后面顺序地连接一个测试结果为1的蚂蚁(结点).由引理1以及表1，可以判断出测试结果为0的蚂蚁(结点).与此同时，测试结果为1的蚁群(结点集)S应满足1≤|S|≤t.

第2步.继续按顺时针方向来检测蚂蚁(结点)的测试结果.如果蚂蚁(结点)的测试结果为0，返回第2步，反之，进行第3步.

第3步.继续按顺时针方向来检测蚂蚁(结点)的测试结果.如果蚂蚁(结点)的测试结果为1，返回第3步.如果蚂蚁(结点)先前没有被检测，且其测试结果为0，则将其标注为X并返回第2步.如果蚂蚁(结点)先前已被检测，则算法结束.

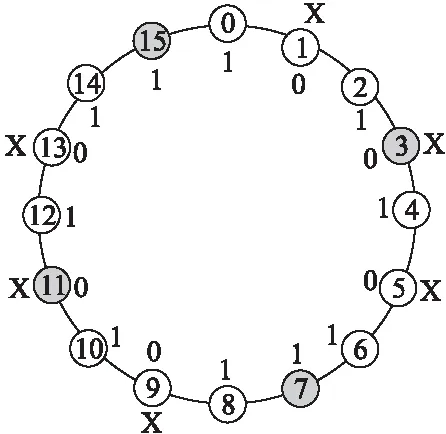
图2 由16个蚂蚁(结点)构成的ACS环Fig.2 ACS ring composed of 16 ants(nodes)

由算法2得到的每一个序列都是由按顺时针方向标注的两个X之间的蚂蚁(结点)以及连接这些蚂蚁(结点)的路径(边)构成.显然，被标注为X的蚂蚁(结点)是一个序列的头结点，同时也是另一个序列的尾结点(见图2)，其中灰色代表故障结点，白色代表无故障结点.

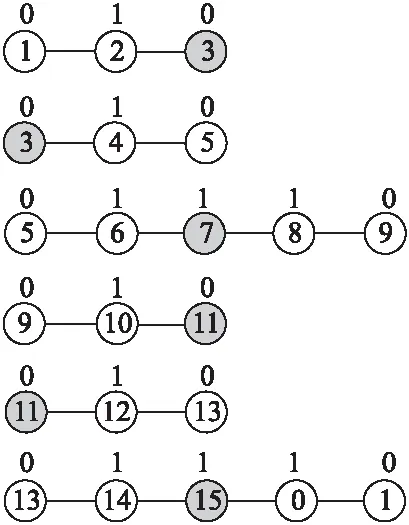
图3 由算法2得到16个蚂蚁(结点)构成的序列Fig.3 Sequences of 16 ants (nodes) by algorithm 2

将图3中的结点如表2所示.

综上所述，得到如下属性：

性质1.序列的测试结果为如下形式：0…01…01…0，且如果序列由三个结点组成，那么测试结果为010.

性质2.每一个序列至少存在一个故障结点.

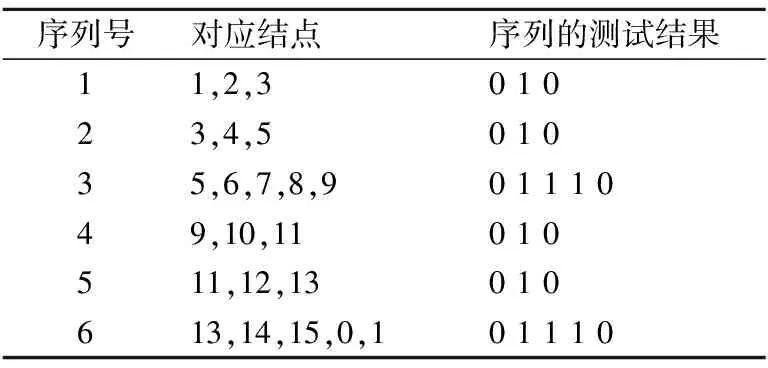
表2 算法2得到的序列表Table 2 Sequence table obtained by algorithm 2

性质3.如果一个ACS环由n个结点构成，且其存在的故障结点个数为t(n≥3t+1)，依据算法2，将其分割为s个序列，那么2t≥s.

定理1. 序列由x个测试结果为0，y个测试结果为1的结点构成，则其满足如下条件：

1)在序列中，如果头结点是无故障的，那么前x个连续的结点也是无故障的且第x+1个结点是故障的.

2)在序列中，如果头结点是故障的，那么前x-1个连续的结点也是故障的.

证明：依据算法2，表1以及引理1得证.

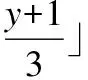
证明：因为序列的头结点是故障的，由定理1得到此序列的前x-1个连续的结点也是故障的.考虑序列中剩余的y+1个结点的情况：

情况1.y=1，很明显引理2是正确的.

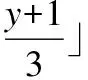
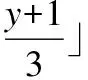
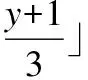
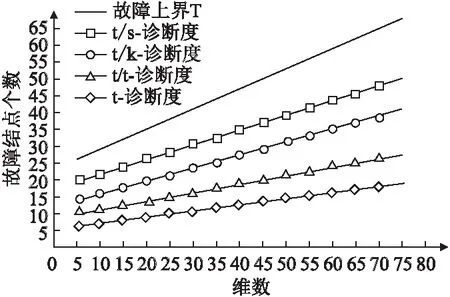
图4 算法2下超立方体网络的4种策略诊断度Fig.4 Four strategies of the hypercube networks under the algorithm 2

可见在环诊断算法下，超立方体网络的t/s-诊断度大于t/k-诊断度大于t/t-诊断度大于t-诊断度.由此可见ACS的环分割策略也同样适用于以超立方体网络为基础的变体立方体网络.

3.2 基于MM模型下ACS的快速精确诊断算法

为了尽可能多地找到ACS中的故障结点，需要用到深度优先算法.对于一个至多存在t个故障结点的n-环，DAS总能输出集合M(|M|≥t+1)，且M中的每一个结点在M中至少存在两个邻居结点.那么，可以把M看做一个无故障结点集.

算法3.MM模型下ACS的深度优先检测

输入：无向图G(V,E)表示由n个蚂蚁(结点)构成的系统，且结点va∈V,vb∈V,令M={v}.

输出：一个子集M⊆V.

第1步.DAS(v)：对于任意的两个结点va,vb(va,vb∈N(v))且va≠M(或vb≠M).

如果ω(v:va,vb)=0.

那么M=M∪va且DAS(va).

第2步.输出集合M中的结点.

由算法2可知系统中的所有结点都能被正确地诊断.

算法4.MM模型下ACS的快速定位诊断

输入：无向图G(V,E)表示由n个蚂蚁(结点)构成的系统，T表示故障结点集的上界,ω表示症状.

输出：一个故障结点集F，一个无故障结点集R，且F∪R=V.

第1步.令Mi=φ(1≤i≤n)，R=F=φ.

如果|Mi|≥t+1,

那么R=R∪Mi.继续进行第2步.

第2步.通过诊断结果ω(vk:va,vb)来鉴别结点ξ∈N(Mi)，其中vk,vb∈Mi.如果ξ是故障的，那么F=F∪{ξ}.反之,Mi=Mi∪{ξ}.重复第2步，直到N(Mi)⊆F.

第3步.如果V=R∪F,那么输出无故障结点集R以及故障节点集F.反之，跳到第4步.

第4步.令R=V-F，输出无故障结点集R和故障结点集F.

4 仿真实验

选用Matlab进行仿真实验，系统Windows10，软件平台Matlab 7.0.4,硬件环境：X86架构且支持SSE2指令集，硬盘空间4G，内存2G.基于算法1，分别取蚂蚁个数M=30,70,100，运行Matlab，得到的实验结果如图5，图6，图7所示.

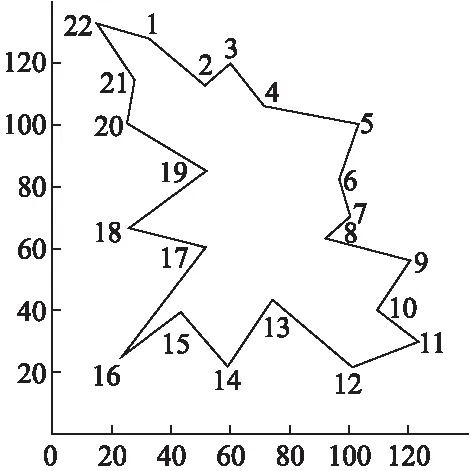
图5 ACS中取蚂蚁个数为30的觅食最优路径
Fig.5 Optimal feeding path of 30 ants in ACS

通过仿真实验得到蚂蚁M觅食的最优路径(如图5，图6，图7所示).随着实验次数以及蚂蚁数目的不断增加(无限趋于n)，将得到一条更趋近于环的最优路径，且得到的路径逐渐趋于稳定.

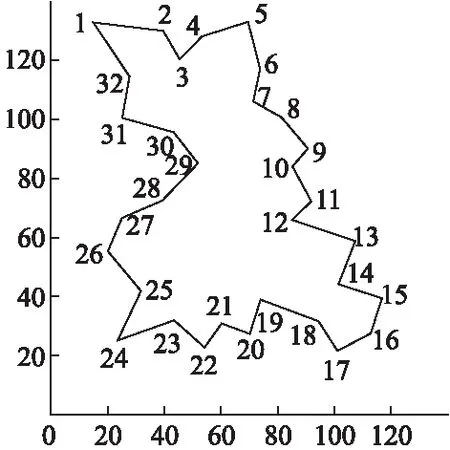
图6 ACS中取蚂蚁个数为70的觅食最优路径
Fig.6 Optimal feeding path of 70 ants in ACS

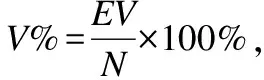
在N-ACS环中取5组不同的Q1，Q0值.得到的结果如表3所示.表3的实验结果显示，Q1，Q0的取值不影响N-ACS环的诊断结果，且对于任意的ACS环，运用算法2的ACS环诊断算法，能够通过已诊断出的无故障结点诊断出可能存在的故障结点.

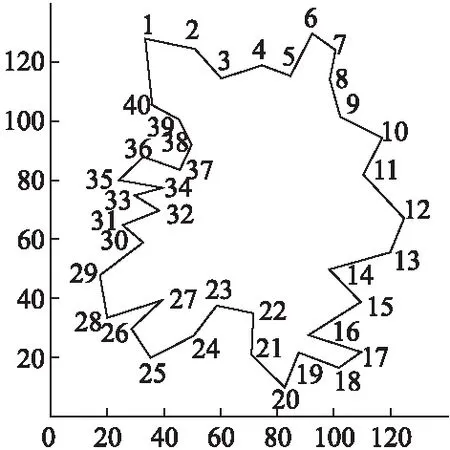
图7 ACS中取蚂蚁个数为100的觅食最优路径Fig.7 Optimal feeding path of 100 ants in ACS

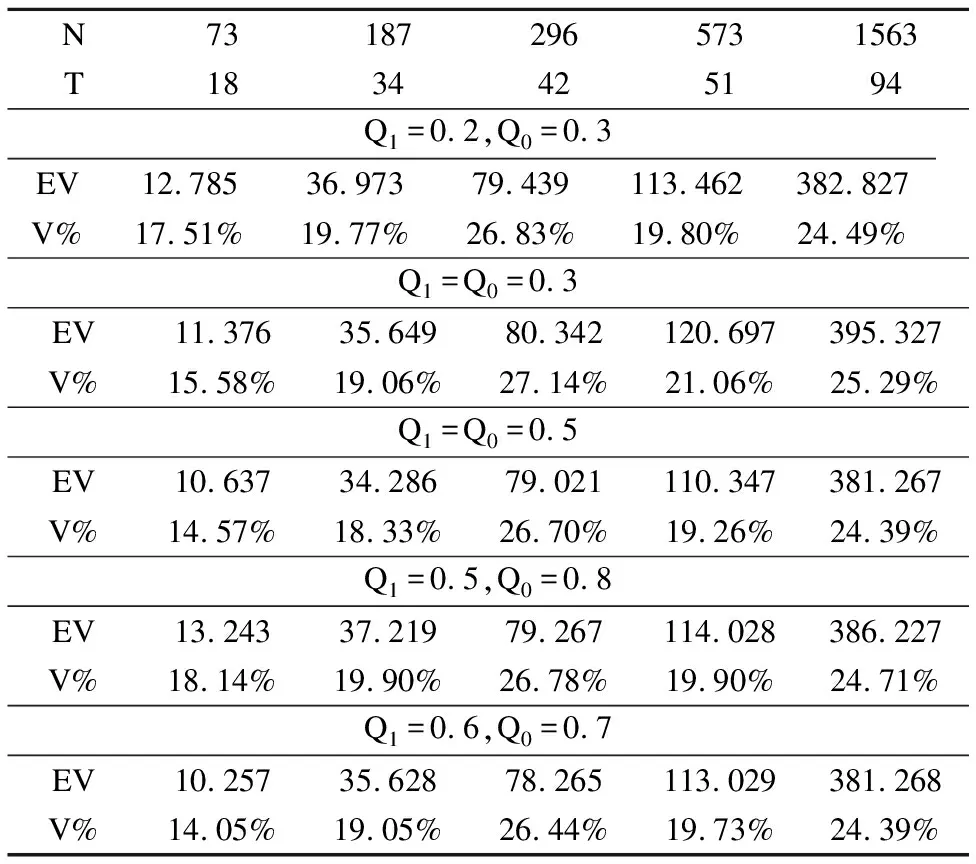
表3 ACS环中Q1，Q0取不同值的统计数据Table 3 Statistics of different values of Q1and Q0in ACS ring

基于以上实验结果，将Q1，Q0的初始值都设为0.3.运行Matlab，对结点进行检测以及定位，经过多次仿真实验，得到的实验结果如图8所示.可见系统中存在的故障结点数与诊断出的故障结点数趋同.

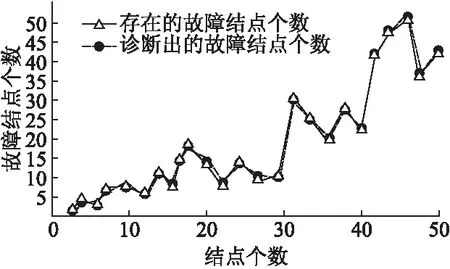
图8 MM模型下算法3、算法4的测试结果Fig.8 Test results of algorithm 3 and algorithm 4 under MM model

定理2.MM模型下ACS的快速精确诊断算法的时间复杂度为O(N)，其中N为蚁群中蚂蚁的数量.

证明：用F表示系统中存在的故障结点集，R表示剩余V-F的集合.若结点v属于V-F集合，则在算法3、算法4中，第1步的时间复杂度为O(N).若节点v属于R∪F，则在算法3、算法4中，第1步的时间复杂度为O(N).因此，在算法3、算法4中，第1步的时间复杂度为O(N).第2步以及第3步的时间复杂度为O(N).算法4的第4步，时间复杂度也为O(N).因此，总的时间复杂度为O(N).

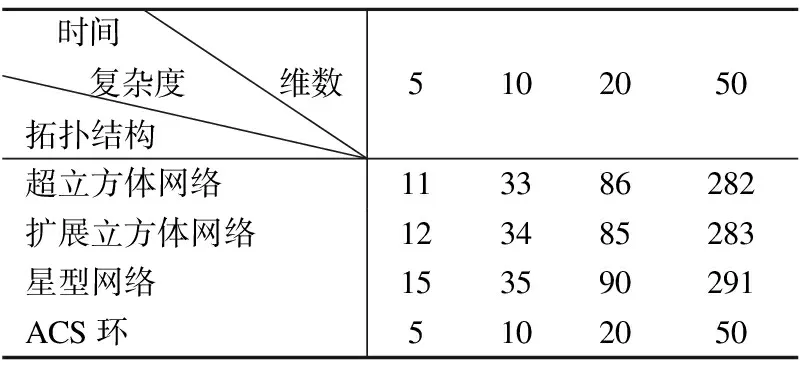
表4 几种网络拓扑结构的时间复杂度比较结果Table 4 Comparison results of time complexity for several network topologies

目前，基于比较模型下ACS环的故障诊断度以及故障诊断算法还没有学者研究，故本文提出的方法是较为新颖的，且与超立方体网络[10,11]、扩展立方体网络[12]以及星型网络[13]相比，本文提出的算法时间复杂度更小(比较结果见表4).

5 结 论

本文在蚂蚁觅食行为的启发下，形象的将蚂蚁作为系统中的结点，蚂蚁之间通过释放信息素而得到的路径作为结点之间的连接，结合图论，对蚁群系统(ACS)进行了深入研究.通过对蚁群系统中蚂蚁觅食路径的算法分析，由大量仿真实验，且随着蚂蚁数目的不断增多(无限趋于n),得到一条更趋近环的觅食最优路径，并对此路径进行环分割，从而得到一系列的序列.通过分析，得到关于序列的一些重要属性，基于这些属性，提出了ACS系统在MM模型下的快速精确诊断算法，通过大量仿真实验，得出ACS中存在的故障结点数与诊断出的故障结点数趋同，且时间复杂度为O(N)，其中N为蚁群系统中蚂蚁的数量.

对于解决类似问题的(如TSP(旅行商问题)，蝙蝠的回声定位问题等)故障诊断，本文的研究方法同样适用.未来研究以ACS为基础的扩展问题(如TSP)的t/t-诊断度、t/k-诊断度以及t/s-诊断度，本文的研究思路同样适用.