太赫兹频段雷达探测的冰云微物理参数反演算法模拟研究

丁 霞，黄兴友，王海涛

（1.上海无线电设备研究所，上海200090；2.上海目标识别与环境感知工程技术研究中心，上海200090；3.南京信息工程大学，江苏南京210044）

1 引 言

冰云由各种球形、非球形的冰晶粒子组成[1]，对地球-大气系统的辐射收支平衡和水汽循环有重要的调节作用，其特征参数，如云厚、范围等宏观参量，以及冰晶粒子大小、形状、数浓度、冰水含量、粒子谱分布等微观参量的精度直接影响其散射辐射特性描述的准确性[2-3]，从而影响到气候模式、遥感探测、大气探测等的结果[4-5]，因此冰云观测及特征参数反演研究有着非常重要的意义。

冰云粒子散射能力弱，只有高灵敏度的探测设备才能进行冰云的探测，目前主要采用Ka波段(35 GHz)和W波段(95 GHz)毫米波云雷达，它们在观测非降水云和弱降水云方面有显著优点[6]，并且开发了针对这些频段的相关产品的反演算法[7-8]，但Ka和W波段雷达对高空冰云(卷云)的探测能力有限，难以探测薄卷云。根据散射理论可知，尺度很小的冰云粒子，对短波长电磁波的散射能力更强，因此，可考虑用更短波长的毫米波或亚毫米波雷达进行卷云探测。

太赫兹(THz)波是指频率在0.1～10.0 THz范围内的电磁波，对应波长范围为0.03～3.00 mm，位于微波和红外波段之间，该频段的雷达波长更接近冰云粒子尺寸，在理论上具有更高的探测能力和灵敏度[9-10]，适合于星载平台以及含水量相对少的高纬度地区或高空区域的气象遥感探测，从而实现冰云三维结构的高精度测量[11-12]。采用太赫兹雷达探测冰云，需要开发适合太赫兹遥感反演冰云微物理参数的算法，以求获得可靠的冰云产品，满足云物理研究、气象保障的需求。冰云粒子在太赫兹波段和Ka波段及W波段具有不同的散射特性[13-14]，冰云粒子的后向散射特性与雷达回波功率的关系也有所不同。因此，在太赫兹云雷达用于冰云的观测和数据反演业务之前，需要模拟验证反演算法的可靠性。考虑到大气的吸收和衰减特性，220 GHz是一个可用的太赫兹波雷达频段，国内外正在积极开展太赫兹主动云雷达样机研制工作，因此，本文针对220 GHz的G波段雷达探测的冰云微物理参数反演方法进行了模拟验证研究。

国内外许多学者对毫米波云雷达的云微物理参数反演算法进行了研究，Liu等[15]统计了W波段云雷达反射率因子(Z)与冰水含量(IWC)之间的经验关系，Hogan等[16]为提高反演精度，在Z-IWC经验关系中引入大气温度，Protat等[17]统计得出了Ka及W波段云雷达在不同纬度的Z-IWC经验关系。根据这些经验关系，樊雅文等[18]反演研究了不同云况下云水含量、冰水含量和云滴有效直径的垂直分布情况，王金虎等[19]从粒子散射特性上着手，研究了冰晶粒子模型对于毫米波云雷达的雷达反射率因子反演冰水含量的影响。利用经验关系反演的优点在于计算简单，但经验系数的选取条件性强，算法适用性和扩展性较差，因此，Benedetti等[20]提出将最优估计理论用于星载云雷达CloudSat/CPR的冰云微物理参数的反演研究，Austin等[21]在此基础上开发了一种应用于CloudSat/CPR的云微物理参数的业务化反演算法，用于全球云微物理参量的反演。Deng等[22]和Delanoё等[23]也基于该理论，利用CloudSat和CALIPSO的探测数据联合反演得到冰云有效粒子半径和冰水含量。受观测数据所限，目前尚无太赫兹雷达探测的冰云数据，也没有利用太赫兹雷达数据反演冰云微物理参数的适用方法。

在忽略冰晶粒子对太赫兹信号的衰减和多次散射等条件下，本文基于最优估计理论进行太赫兹频段的冰云反演算法研究，并模拟验证其可靠性。假设冰云粒子为球形，粒子谱服从对数正态分布，根据冰晶粒子在太赫兹波段的散射特性，建立对应的前向物理模型，并基于最优估计理论进行冰云微物理参数反演，获得了冰云微物理参数，与模拟计算设定的粒子谱参数相比，分析反演误差，说明该算法应用于太赫兹云雷达的冰云微物理参数反演的可行性和可靠性。

2 基于最优估计理论的冰云微物理参数反演算法

2.1 前向物理模型

云粒子谱分布表示了冰晶大小与粒子数浓度的关系，谱分布主要有对数正态分布、伽玛分布、双峰伽玛分布、幂指数分布等，目前云粒子计算中最常用的是对数正态分布和伽玛分布，研究表明这两种分布可很好地模拟云粒子的尺度分布情况，也经常应用到云微物理参数反演研究中。本文采用对数正态分布来进行太赫兹频段的冰云微物理参数反演研究。分布函数见公式(1)，

式中：NT是粒子数密度；D为粒子直径；Dg为几何平均直径；σ是分布宽度参数，为无量纲变量；ln代表自然对数。

粒子分布可由NT、σ和Dg三个参数来表示，经公式推导，云中冰水含量IWC和有效粒子半径re也可表示为这三个参量的函数[21]，见公式(2)和公式(3)，

计算太赫兹(220 GHz)频段米散射截面与瑞利散射截面的比值可知，当D＜228 μm时，两者比值在0.9～1.0之间，可认为米散射与瑞利散射相当，认为冰云粒子尺寸满足瑞利散射条件，雷达反射率因子ZRay的定义公式如下，

随着粒子尺寸变大，比值逐渐减小，特别是当D＞579 μm时，两者比值小于0.1，如果继续采用瑞利假设计算雷达反射率因子，会导致结果高出实际值，产生误差。为修正该误差，引入冰云粒子实际散射与瑞利散射的比值f，即f=Ze/ZRay，其中Ze表示实际的雷达反射率因子，ZdB=10log10Ze。

参考Austin等[21]提出的方法，将针对冰云的雷达反射率因子转化为水云的雷达反射率因子，以便与通常的雷达反射率因子的含义一致，m为水或冰粒子的复折射指数，引入的比值对前向模型进行修正。对于水和冰的介电特性前人做了很多研究，计算方法相对成熟，本文分别采用Ray[24]和Matzler[25]总结的方法对水和冰的复折射指数m进行运算，并得到对应的Kice和Kliq，进而得到雷达反射率因子。综上所述，在不考虑衰减和多次散射的理想情况下，前向模型F(x)可表示为公式(5)，

采用离散偶极子近似法 (Discrete Dipole Approximation，DDA)计算冰晶粒子的散射性质[26]，依据散射波信号的可加性原理，以及冰云粒子谱分布，在不考虑衰减和多次散射的理想情况下，计算得到雷达反射率因子ZDDA，该值相当于实际的雷达反射率因子Ze，

其中，σbk表示粒子直径D的球形粒子的后向散射截面。

图1a为220 GHz雷达反射率因子 (ZDDA)，横坐标为粒子有效半径re，图1b的横坐标为粒子尺度参数α=πD/λ，展示了比值f随粒子尺寸的变化。由图1可知，随着粒子尺寸的增大，f减小，与Benedetti等[20]文中图1的冰云粒子在94 GHz米散射与瑞利散射的比值变化趋势基本一致。

2.2 最优估计理论

测量向量y为雷达反射率因子ZdB，未知的状态向量x为三个待反演参数：粒子数密度NT、几何平均直径Dg和分布宽度参数σ。通过太赫兹频段云粒子前向物理模型F(x)建立两者之间的关系，可表示如下，

式中：n为雷达廓线的总距离库数，z1和zn分别代表雷达廓线中云底和云顶的距离库；ZdB(zi)、Dg(zi)、NT(zi)和σ(zi)分别代表雷达反射率因子、几何平均半径、云粒子数密度和分布宽度参数在距离库 zi处的值，可简写为 ZdBi、Dgi、NTi和 σi。

代价函数表示状态向量和先验数据差分以及已知测量向量和前向模型值差分的加权之和，如公式(8)所示，最优估计算法在代价函数取得最小值的情况下求得最优解。对于每条观测廓线，待反演变量(状态向量x)为每个距离库的三个云物理参数，已知测量向量y仅有对应距离库内的雷达反射率因子，因此需要借助先验数据对反演过程进行约束，保证迭代收敛以及反演结果的可靠性。

式中：上标T表示矩阵的转置，xa为先验数据，Sa为先验数据的协方差矩阵，矩阵Sa的对角元素为xa中三个参数在距离库zi处的方差，Sy为系统测量误差协方差矩阵。

通过连续最小化代价函数，可得到状态向量的迭代解，运算得到每个距离库的待反演变量。

式中：上标i和i+1表示迭代次数，先验数据xa将作为迭代初值进行运算，本文采用计算粒子散射特性时设定的粒子谱参数作为先验数据，Sa则选择CloudSat云雷达反演所采用的误差值[21]和的值分别为 0.226、0.555和 0.235。矩阵L代表前向物理模型对状态向量的灵敏度，见公式 (10)，根据太赫兹频段云粒子前向模型表达式，可计算矩阵各项的值，

迭代的收敛条件设置为[21,27]，

式中：Δxˆ表示xˆi+1和xˆi的差值，3n 为状态向量 x 的维数，Sx是迭代状态向量的误差协方差矩阵，该矩阵的对角元素为反演参量的方差，而非对角元素为反演参量之间的协方差，根据公式(2)和公式(3)中IWC和re的计算方法，误差传递得到两者的反演不确定度的计算公式，

在上述说明中，反演算法研究对象为观测廓线，ZdBi、Dgi、NTi和 σi的下标 i表示对应的距离库数，i的取值范围为1～n，其中n为雷达廓线的总距离库数。本文的待反演量NT、Dg和σ，以及测量值ZdB均为单个高度点上的值，即雷达廓线的总距离库数n为1，最优估计反演算法模拟研究在单个距离库上进行。

3 太赫兹频段冰云微物理参数反演验证数据

卷云中冰晶粒子形状多样，散射特性复杂，常见的粒子通常有聚合物状、子弹玫瑰状、柱状、板状、球状等，随着冰云层的高度、气压、温度、冰晶粒子浓度等因素的变化而变化。目前还没有一套能够计算所有形状和所有尺寸粒子散射特性的理论。气象上云滴粒子一般可近似地看作是圆球形，而且球形粒子的散射理论研究已相当系统而完整，已在现有反演算法研究中得到广泛应用，因此本文假设冰云粒子为球形粒子。冰晶粒子尺寸从几微米到几千微米，在1993年进行的赤道太平洋中心区试验中 (CEPEX)，冰晶尺度范围为10～2 000 μm，Hong利用DDA计算了六种冰晶粒子的散射特性数据[1]，设定粒子最大尺度范围为2～10 500 μm。根据 Lynch 的总结[28]，粒子最大尺寸在 1～8 000 μm 之间，典型值为 250 μm，粒子数密度在0.1～107 m-3范围内。

在模拟计算冰云粒子微物理参数及反演研究过程中，设定冰云粒子的直径范围为2～3 800 μm，计算冰晶粒子在220 GHz的散射特性参数σbk，粒子满足对数正态分布，不考虑衰减和多次散射的理想情况下，计算单个距离库上的太赫兹雷达反射率因子Ze(模拟计算的ZDDA)，并由公式(2)和公式(3)分别计算得到冰水含量IWC和有效粒子半径re。记录设置的粒子谱分布参数NT、σ、Dg和对应计算得到Ze、IWC、re为真值，用于反演计算和模拟验证分析。

3.1 反演用例1

任意选取粒子谱参数NT、σ和Dg，由上述方法计算得到Ze、IWC、re的真值，建立反演用例1的数据 (表1)。Ze和 IWC随粒子谱参数NT、σ和Dg增加而增大，粒子有效半径大小同时受σ和Dg影响。在6个反演个例中，Case1～Case5的冰云粒子尺寸均在范围内，而在Case6中，粒子谱分布在3 800 μm处有0.003 m-3的粒子数。

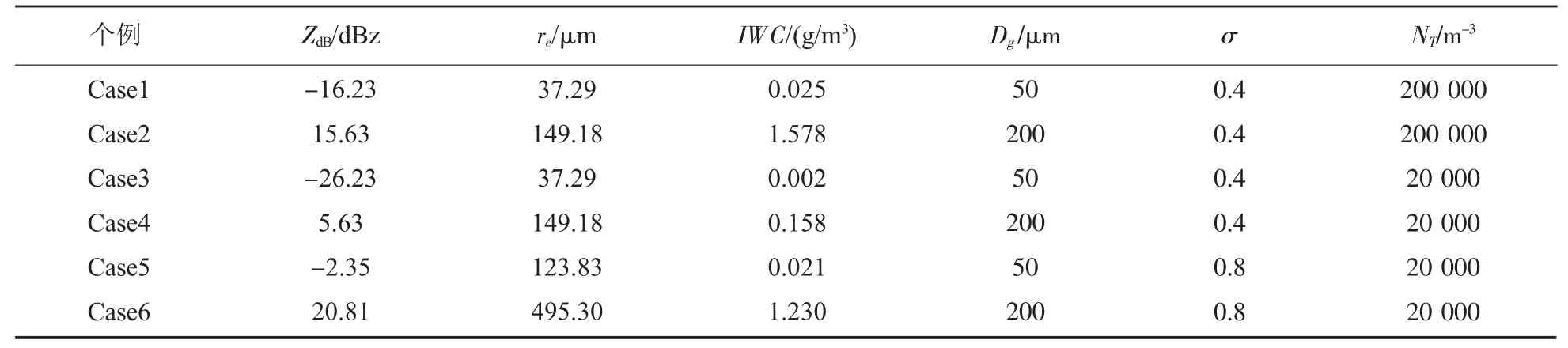
表1 太赫兹云雷达反射率因子及其粒子谱参数信息

3.2 反演用例2

为更全面地分析最优估计反演算法的性能，设定 NT和σ为定值，Dg变化范围为 10～2 400 μm，根据太赫兹频段冰云粒子的散射特性计算得到单个距离库上的Ze、IWC、re，建立反演用例2的数据库。

图2中点线对应有效粒子半径为372.96 μm时的粒子谱分布情况，实线对应有效粒子半径为820.50 μm时的粒子谱分布，虚线表示有效粒子半径为1 790.20 μm的粒子谱分布。

计算可知，点线表示的冰云粒子大小完全在设定范围内，实线表示的粒子谱分布在3 800 μm处有0.04 m-3的粒子数，虚线表示的粒子谱分布在3 800 μm处有2.62 m-3的粒子数，部分粒子大小超出该范围，而大粒子产生雷达反射率因子不可忽视，因此可能对反演结果产生影响。

4 算法设计和验证分析

4.1 算法设计

基于最优估计理论，利用太赫兹频段(220 GHz)的冰晶粒子散射特征参数，设计冰云微物理参数反演的具体流程，算法流程可分为3个部分(图 3)。

4.1.1 数据预处理

利用冰晶粒子在220 GHz散射特性参数σbk，在不考虑衰减和多次散射的理想情况下，根据设置的粒子谱分布参数NT、σ、Dg，计算得到单个距离库上的Ze(模拟计算的ZDDA)、IWC和re。设定的NT、σ、Dg和对应的 Ze、IWC、re作为真值保存。计算冰云粒子实际雷达反射率因子与瑞利假设下雷达反射率因子的比值f，以及水和冰的复折射指数m，并得到Kice和Kliq，将真值Ze作为测量值y，设定的NT、σ、Dg作为先验数据xa和迭代初值，并设定协方差矩阵Sa和Sy。

创新平台的建设首先体现了产学研合作机制，有利于将研究成果与工业生产相结合，是我国化肥工业完成结构性改革中实现技术改变首选的路径；其次体现了企业和大专院校对社会责任的担当。我国在世界上磷资源占有比例不高，磷资源的高效利用是无法回避的问题。长江经济带沿线的化肥企业充分利用资源，实现可持续发展，既是对环境保护的贡献，也能够为企业的市场定位打开新的通道。

4.1.2 迭代计算

迭代计算基于最优估计理论进行，逐步完成各变量的计算，包括前向物理模型值F(x)、L矩阵和迭代状态向量的误差协方差矩阵Sx，完成迭代新值的计算，判断迭代次数是否大于20次，如果是，则计算无效，舍弃，否则判断是否满足收敛条件，如果满足则迭代计算完成，进行下一步，如果不满足，继续进行迭代计算，直到迭代次数小于20次，且满足收敛条件为止，否则计算无效，舍弃。

4.1.3 反演结果和误差计算

根据迭代新值，反演得到单个距离库上的冰云微物理参数 NT、σ、Dg，计算得到 IWC 和 re，与真值比对，计算反演误差值，完成反演及验证过程。

4.2 用例1反演结果分析

由表1可知，任意设置的粒子谱分布参数NT、σ、Dg和计算得到 Ze、IWC、re均为单个距离库上的值，因此文中的反演计算过程也是针对单库进行反演验证。Benedetti等[20]在研究基于最优估计算法的毫米波雷达冰云微物理参数反演时，采用卷云微物理模型[29]的模拟值进行算法验证，本文为定量分析最优估计理论算法性能，将220 GHz冰云粒子散射特性参数的计算值作为真值，分析反演结果与真值的一致性，计算反演结果与真值的偏差(|反演值-真值|/真值)作为反演误差。

表2展示了用例1的反演结果，冰云微物理参数反演结果与真值相同或相近，re反演误差在0～8.81%之间，σ 反演误差在 0～2.5%之间，NT反演误差在0.02%～0.89%之间，不同粒子谱分布情况下反演误差有所变化。在Case1～Case5中，云粒子谱参数和IWC的误差都很小，证明了最优估计反演算法的可靠性。在Case6中，IWC误差达到42.2%，该误差可能是由超出范围内的大粒子所导致的。

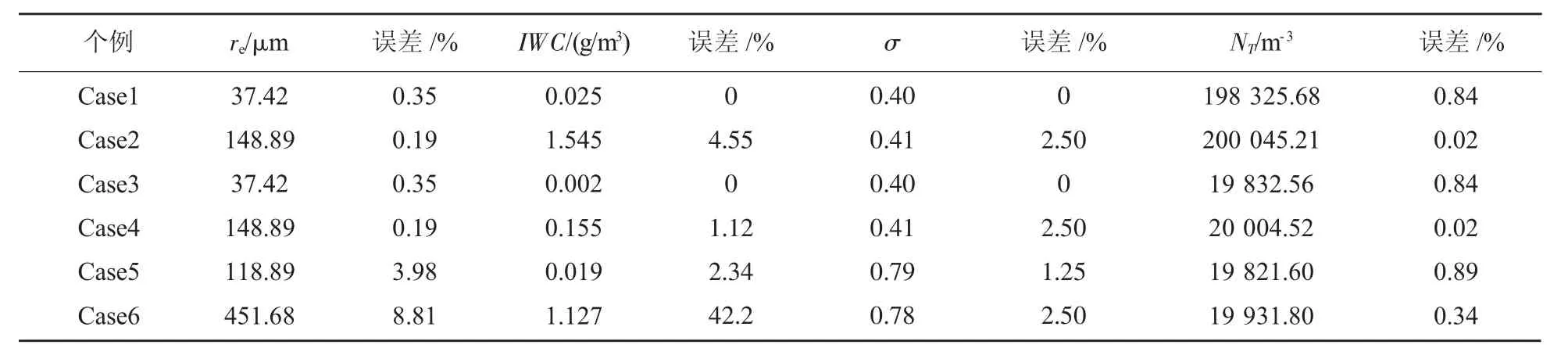
表2 云粒子反演结果及误差

由公式(12)可知，误差协方差矩阵Sx受先验数据xa和系统测量误差的影响，由Sx可得到三个反演参量的方差，以及三者之间的协方差，计算得到IWC和re的反演不确定度及其百分比值 (不确定度/真值)。反演得到的NT不确定度在5×10-4%～8×10-4%之间，σ不确定度的平均值为0.17%，IWC不确定度在8%～67%之间，平均值为44%，re不确定度的平均值为10%。算法收敛速度与迭代初值(xa)贴近真值的程度有关，在迭代初值等于真值时，迭代次数一般为1次，迭代次数随迭代初值与真值的偏差增加而增加，经多次迭代运算后可得到贴近于真值的反演结果，说明准确的先验数据可减少最优估计算法的迭代次数，提高计算效率，与Deng等[22]得出的结论一致。但当迭代初值与真值的偏差超出误差设定范围Sa时，算法一般无法收敛，计算结果被舍弃。

4.3 用例2反演结果分析

图4、图5、图6和图7分别展示了反演得到的 re、IWC、σ 和 NT(实线)，及其真值(虚线)。由图4可知，当re小于400 μm时，误差趋近于0，证明了最优估计反演结果的可靠性，在此范围外，由于大粒子对雷达反射率因子的影响，导致反演结果小于理论值。同样，当re大于400 μm时，σ反演结果小于模拟值(图5)，偏差最大值为0.025，NT反演结果也小于模拟值，偏差范围在0～0.004个量级之间(图6)，且误差随re增大而增加。IWC在re大于400 μm时开始出现偏差(图7)，且随re增大而增加，偏差范围在0～0.1个量级之间。综上可知，在re小于400 μm时，re反演误差小于0.04%，σ的反演误差小于0.02%，NT反演误差小于0.50%，IWC反演误差小于0.08%，模拟研究结果证明，在不考虑衰减和多次散射的理想情况下，最优估计反演结果与模拟值具有良好的一致性。

当re大于400 μm时，云粒子谱参数反演误差随re增加而变大，re反演误差上升到10%，NT反演误差上升到1%，σ反演误差上升到6%，IWC反演误差可达到22%，这是由于在进行太赫兹波段云粒子后向散射特性计算时，没有考虑粒子直径大于3 800 μm的情况。由图8可知，单个半径大于1 800 μm的粒子可导致10 dB左右的雷达反射率因子计算误差，那么如果云粒子谱分布超出范围(有效直径大于3 800 μm)，部分大粒子没有考虑进去，计算得出的雷达反射率因子偏小，从而导致了冰云微物理参数的反演误差。

按用例1中的方法，由协方差矩阵Sx计算用例2中的NT、σ、IWC和re的反演不确定度百分比值。NT的平均不确定度为0.005%，σ的平均不确定度为4.55%，IWC的平均不确定度为12.80%，re的平均不确定度为4.61%。与用例1一样，算法收敛速度与迭代初值贴近真值的程度有关，在迭代初值等于真值时，平均迭代次数一般为1次，迭代次数随迭代初值与真值的偏差增加而增加，由冰云粒子微物理模型导致的粒子尺寸误差一般小于20%[22]，在 re小于 400 μm 的前提下，在此范围内随机设置迭代初值与真值的偏差，只要其偏差不超出误差设定范围Sa，最优估计算法经多次迭代运算后得到贴近于真值的反演结果，平均迭代次数一般不超过10次。

5 结 论

本文基于最优估计理论进行太赫兹频段(220 GHz)的冰云微物理参数反演算法研究，并模拟验证其可靠性。根据冰晶粒子在太赫兹波段的散射特性，计算出了冰云的雷达反射率因子，及其与瑞利假设下雷达反射率因子的比值，建立前向物理模型，基于最优估计理论进行冰云微物理参数反演，分析反演结果的不确定度，以及反演结果与模拟计算真值的误差，证明该算法应用于220 GHz云雷达的冰云微物理参数反演的可行性和可靠性。

论文采用两个反演用例来进行反演计算和验证研究。假设冰云粒子为球形，粒子谱服从对数正态分布，不考虑粒子衰减和多次散射的影响，将冰云散射特性参数的模拟计算值，包括设置的粒子谱分布参数NT、σ、Dg，以及计算得到单个距离库的Ze、IWC、re作为真值，分析反演结果与真值的一致性，计算反演误差。在用例1中，利用随机设定的6种冰云粒子谱个例进行最优估计反演算法的性能分析，其中，Case1～Case5的冰云粒子大小均在设定范围内，有效粒子半径re的反演误差小于4%，粒子谱宽σ的误差小于2.5%，粒子数密度NT误差小于1%，IWC误差小于5%，说明了最优估计反演结果的可靠性。在用例2中，假设NT和σ为定值，通过对反演结果及误差随粒子尺寸的变化情况分析，表明了当冰云粒子尺寸在太赫兹波段云粒子后向散射特性计算的范围内时，re误差小于0.04%，σ误差小于0.02%，NT误差小于0.50%，IWC反演误差小于0.08%，说明在不考虑衰减和多次散射的理想情况下，最优估计反演结果与理论值具有良好的一致性。在re大于400 μm时，云粒子谱参数反演误差随re增加而变大，与Case6一样，这是由于在进行雷达反射率因子模拟计算真值时忽略了直径大于3 800 μm的粒子。

反演结果的不确定度由Sx计算得到，两个用例的冰云微物理参数反演结果的不确定度都比较小。迭代初值的设置对反演算法的收敛速度有重要影响，在迭代初值等于真值时，平均迭代次数一般为1次，迭代次数随迭代初值与真值的偏差增加而增加，只要其偏差不超出误差设定范围Sa，多次迭代运算后仍然可得到贴近于真值的反演结果，说明准确的先验数据可减少最优估计算法的迭代次数，提高计算效率。上述研究表明基于最优估计理论的冰云微物理参数算法反演结果与模拟计算真值具有良好的一致性，反演结果的可靠性高，该算法对于太赫兹云雷达冰云观测和微物理参数反演研究的迫切需求具有实用意义。