湖南省近54年冬季降水分区及趋势分析

胡 倩,贺新光,2,卢希安,章新平,2

(1.湖南师范大学资源与环境科学学院，湖南长沙410081；2.湖南师范大学地理空间大数据挖掘与应用湖南省重点实验室，湖南长沙410081)

1 引 言

IPCC第五次报告指出，全球地表平均气温在近百年里上升了0.85℃，全球气候变暖已成为一种趋势[1]。受全球气候变暖和人类活动的影响，水文循环过程发生了显著的变化。降水是水文循环过程中重要的环节，对区域降水进行趋势分析能够为水资源的可持续利用与优化配置提供科学的参考[2-3]。

目前国内外众多学者对降水变化趋势进行了大量的相关研究。Nalley等[4]采用离散小波变换结合MK检验法探讨了加拿大魁北克省和安大略省南部地区降水和径流的变化趋势及影响各自变化趋势的主周期分量。Palizdan等[5]采用离散小波变换结合MK检验法探讨了马来西亚Langat流域的各子区域的降水变化趋势及影响各自趋势的主周期分量。Chen等[6]同样运用离散小波变换结合MK检验法探究了我国黄甫川流域的降水和径流的变化趋势及影响各自趋势变化的主周期分量。王兵等[7]利用小波变换和集合经验模态分解法对广州1908—2010年的月温度和月降水进行多尺度对比分析。郑腾飞等[8]探讨了1961—2010年广东省不同等级降水的空间分布及时间变化特征。有关夏季降水的研究表明：我国长江流域、珠江流域和华南地区夏季降水均呈一定程度的增加趋势，特别是进入1980年代以后，这种增加的趋势变得更为显著[9-12]。然而，目前针对冬季降水的研究相对较少。冬季我国降水主要受东亚季风和ENSO的影响，东亚季风和ENSO异常往往会带来低温、寒潮、冰冻和暴雪等自然灾害[13-16]。对此，不少气象学者对我国冬季降水时空变化特征开展了一些研究[17-18]。如孙建奇等[19]研究发现：由于受到冬季变暖的影响，我国冬季降水呈现出增加的趋势，尤其是在南方地区，其增加趋势更为显著。王林等[14]通过经验正交函数（EOF）分析了我国冬季降水的年际变化特征，表明长江以南地区降水的一致性变化在整体上能够反映出我国冬季总降水量的变化特征。

湖南省属于典型的亚热带季风气候区，受地形等条件的影响，降水时空分布不均，年际变化大。湖南省的冬季降水少且不稳定，但由于冬季盛行西北风（偏北风），可能会导致异常的冬季降水，造成大的灾害[20]。当前，针对湖南省冬季降水变化研究甚少，本研究结合旋转经验正交函数（REOF）与层次聚类法（HCA）对湖南省89个气象站点的冬季降水进行分区，并在分区的基础上运用离散小波变换、MK非参数检验和Sequential MK检验相结合的方法分析湖南省不同子区域的冬季降水变化趋势及影响各自趋势的最占优的周期分量，为湖南省冬季降水的预测及水资源的分配管理提供参考依据。

2 数据资料

本文所采用的数据是由湖南省气象局提供的97个气象站点1960—2013年的逐日降水数据。剔除资料不全和长度不够的站点后，最终选择了89个气象站点（图1），且这89个气象站点的逐日降水数据均通过了均一性检验。根据湖南省的气候特征，将12月—次年2月定为冬季，然后分别计算出这89个站点近54年来逐年的冬季降水序列。各分区的区域冬季降水序列采用基于面积权重的方法计算，其权重系数是每个气象站点所控制的面积范围占整个区域面积的百分比，其通过ArcGIS10.2中的泰森多边形法进行估算[21]。

3 研究方法

3.1 分区方法

经验正交函数（EOF）常用于气象要素场的时空分解，EOF不受气象站点分布的限制，且能够根据气象要素场序列本身的主要特征来确定正交函数形式[22]。旋转经验正交函数（REOF）则是基于EOF对载荷特征向量场做最大正交方差旋转变换，并且能使原始要素场的信息特征集中映射到载荷场所在的优势空间上[23]，进而更清晰地反映出地域的变化特征且在时间上更具稳定性。EOF和REOF的有关数学理论及具体计算过程可参考文献[24]。

层次聚类法（HCA）是一种多变量统计方法，能够将一个数据集划分为若干聚类，并使同聚类中的数据对象比不同聚类的数据对象具有更高的相似度[5]。文中的HCA采用平方欧氏距离测算各站点间距离，选用Ward法计算类间的距离，合理的站点分类数根据Rousseeuw[25]提出的轮廓系数（Silhouette Coefficient，SC）来确定。轮廓系数的取值范围在-1和1之间，当SC趋近于1时，表明聚类数是合理的；当SC趋近于0时，表明聚类数是不确定的；当SC趋近于-1时，表明聚类数是不合理的。总而言之，SC值越接近于1，得到的聚类数越合理。关于轮廓系数的具体计算公式参见文献[25]。

本研究应用Domroes等[26]和Raziei[27]所采用的REOF和HCA相结合的分区方法对湖南省的冬季降水进行分区。该方法克服了REOF在确定载荷值界限时的主观性[28]，使分区结果更具客观性。文中分区的基本步骤是：（1）对湖南省各站点的冬季降水时间序列进行标准化处理后，运用EOF对标准化后的降水时空场进行经验正交分解；（2）根据North等[29]提出的计算特征值误差范围的方法进行显著性检验，并选取通过0.05显著性检验的前几个载荷向量场（空间模态）进行最大正交方差旋转，得到相应的旋转载荷向量场；（3）将所选的旋转载荷向量场作为HCA的分类特征量，并根据轮廓系数值确定合理的聚类数，最终获得湖南省冬季降水的分区结果。

3.2 小波变换

小波变换是一种有效的时域和频域分析工具，可以分析时间序列周期变化的局部特征，因而被广泛用于水文气象等序列的分析。同时，能更清楚地看出各周期随时间的变化规律[4]。本文采用离散小波变换对冬季降水序列进行分解，其详细的计算过程可参考文献[4]。应用离散小波变换可将原时间序列x(t)分解成不同时间尺度下的细节分量Dj(t（)高频信息）和近似分量Aj(t（)趋势信息）子序列。然后，原始时间序列x(t)可以通过细节分量和近似分量重构，即x(t)=Dj(t)+AJ(t)，式中 J是最高分解层数。文献[30]详细介绍了各分解层j的细节分量Dj(t)和近似分量Aj(t)的计算公式。本文采用Daubechies（db）小波对湖南省冬季各分区的降水序列分别进行离散小波变换而计算得出各自的细节和近似分量子序列。

3.3 趋势分析

Mann-Kendall检验是一种非参数检验方法，其样本既不需要遵循一定的分布，也不受少数异常值的干扰[31-32]，常用于水文、气象等时间序列的趋势检测。MK检验的详细介绍参考文献[4,31-32]。季节降水序列的自相关性会影响MK检验的可靠性[26]，因而需要先对数据进行自相关性的显著性检验。当原时间序列与滞后时间序列之间的相关系数r1不显著（没有通过p＜0.05的显著性检验）时，将MK检验用于时间序列，反之将改进的MK（MMK）检验用于时间序列。关于MMK检验的计算过程可参考Hamed等[31]的研究。Sequential MK（SQMK）检验用于检测时间序列趋势的连续变化，是一种对时间序列进行顺序和逆序分析的MK检验，并得出服从标准正态分布的统计量值（u(t)）。u(t)值的具体计算过程参见文献[5-6]。文中主要应用这3种类型的MK检验对湖南省各分区的冬季降水序列进行趋势分析。

4 结果与讨论

4.1 冬季降水分区

对湖南省89个气象站点1960—2013年的标准化冬季降水时空场（54×89的数据矩阵）进行EOF分解，其中，EOF的前3个空间模态通过了0.05显著性检验。然后，旋转这3个EOF模态以获得旋转的空间模态（REOF）。前3个EOF和REOF空间模态的方差贡献率和累积方差贡献率列于表1中，累计解释方差贡献率均达85.49%。从表1中可知：第一EOF模态的方差贡献远大于其它2个模态，表明其在湖南省的冬季降水距平场的变化中占主要的地位；此外，第一REOF模态的方差贡献率也远大于其它的2个模态，表明其是湖南省冬季降水异常分布最占优的模态。

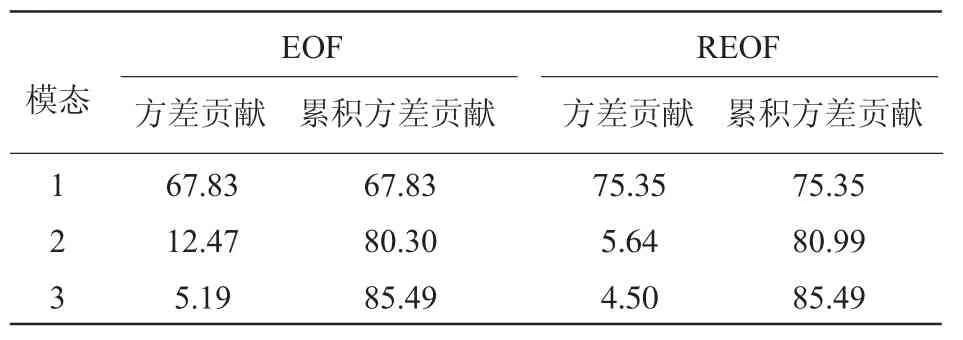
表1 EOF和REOF前3个模态的方差贡献及累计方差贡献(%)

湖南省冬季降水前3个REOF模态的空间分布如图2。第一旋转模态在湖南省的绝大部分地区为正值（图2a），在武陵山脉以南和雪峰山脉以北一带为负值，说明这一带的冬季降水与湖南省其它绝大部分地区呈现出反位相的变化特征。其正的高值区主要位于湘南地区，以南岭地区为中心，中心值达0.25，说明湘南地区的降水变率大且为第一模态的降水异常敏感区。第二旋转模态的值总体上西北高于东南，其负值位于湘中及湘南的部分地区，而在湖南省的其它区域均为正值（图2b），说明湘中及湘南部分地区的冬季降水与湖南省其它地区存在相反变化的特征。该模态显著突出了湘西北的正值区，其中心值达0.26，说明湘西北地区为该模态的降水异常敏感区。图2c为第三旋转模态的空间分布，该模态自西北向东南大致呈“正负正”交替分布，负的高值区位于湘中地区，说明湘中地区为该模态的降水异常敏感区，及湖南省冬季降水在中部与南北地区具有反位相的变化特征。

总体上，湖南省冬季降水的空间特征呈现3个主要的降水异常敏感区：湘南、湘西北以及湘中。这3个降水异常敏感区基本覆盖了整个湖南省，将其对应的旋转空间模态作为HCA聚类的特征量，从而根据SC选取最合理的聚类数。由SC曲线图可知：SC的最大值所对应的聚类数为5（图3），因而湖南省冬季降水可划分为5个子区域。从图4可观察到：湖南省冬季降水的5个子区域在空间上具有明晰的一致性，且每一子区域从西南向东北呈带状分布。然后，沿西北向东南，可依次观察到：DJF1位于湘西北地区，DJF2集中在湘西-湘北地区，DJF3分布于湘西南-湘中地区，DJF4位于湘南丘陵地区，而DJF5则集中在湘南山地区。表2列出了各分区的气象站点数、面积及区域平均冬季降水量。从表2中可知：各分区气象站点数的分布较为均匀，DJF1最多（20个），DJF5最少（15个），但面积占比差异较大，面积占比最大的为DJF2（25.33%），而DJF5最少，仅占 13.42%。而且，区域平均冬季降水量从西北向东南递增，这与我国南方冬季降水的变化特征[33]具有一致性。

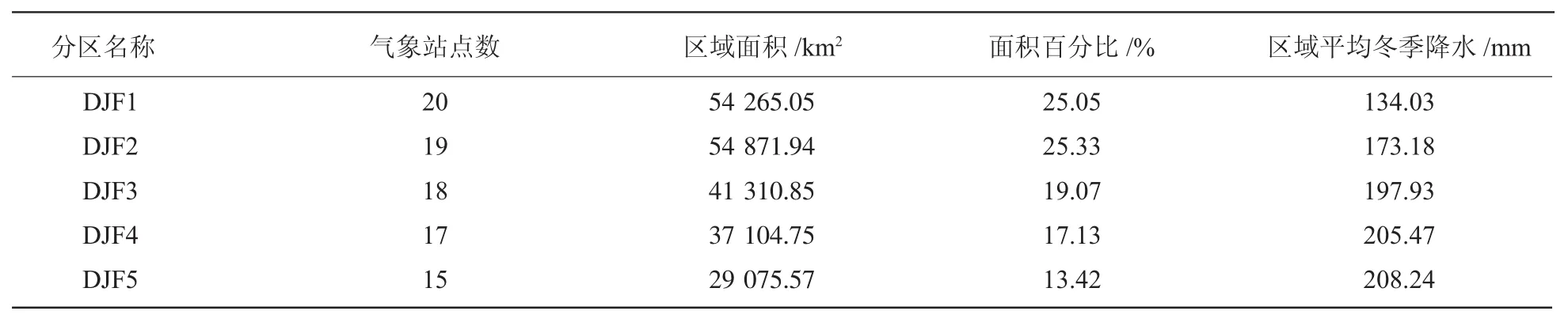
表2 各分区的面积和区域平均冬季降水量

4.2 冬季降水变化趋势

图5 展示了湖南省各分区54年来冬季降水的逐年变化和11年滑动平均曲线及降水倾向率，但各分区的降水倾向率均未达到0.05的显著性水平。从图5可以看出：DJF1呈缓慢的上升趋势，降水倾向率为5.5 mm/(10 a)，1984年之前降水相对偏少，低于冬季多年平均降水量（134.03 mm），1984年之后降水开始偏多，其最大值出现在2003年（252.53 mm）；DJF2也呈不显著的上升趋势，降水倾向率为4.4 mm/(10 a)，与区域DJF1一样，1984年之前的降水相对偏少，1984年之后降水开始偏多，而在2005年之后则呈波动下降的趋势，降水量最大值出现在2005年（312.72 mm）；DJF3的冬季降水具有增加的趋势，降水倾向率为6.6 mm/(10 a)，其降水量的最大值在1998年（368.41 mm），1998年之前的降水偏少，但表现出增加的趋势，而1998年之后的降水呈波动下降的趋势；DJF4整体上呈上升的趋势，降水倾向率达9.1 mm/(10 a)，在1980年之前偏少，1980—1998年降水偏多，1998年之后降水虽然相对偏少，但普遍高于区域平均冬季降水（205.47 mm）；DJF5降水倾向率最大为9.8 mm/(10 a)，1980年之前降水偏少，1980—1998年降水偏多，1998年之后降水有偏少的倾向。由11年的滑动平均曲线可以看出：各子区域冬季降水的年代际变化规律具有相似性，即具有先波动上升后又波动下降的趋势。具体来看，区域冬季降水在1980年代中期之前均呈波动增加的趋势，但降水均偏少，1980年代中期之后降水趋于偏多，但进入21世纪以来，各区域的降水又有偏多转为偏少的倾向。湖南省冬季降水的这种年代际变化与我国南方冬季降水的年代际变化[14]是一致的。此外，正如文献[14]所指出的：这种年代际变化的出现可能与东亚季风强度的年代际变化有关，并受其影响。

4.3 冬季降水趋势的主周期分量

为了避免对数据集进行不必要的时间尺度分解，首先要确定冬季各分区降水序列的最高分解层，然后从最高分解层中找出最优分解层J。根据Kaiser[34]提出的公式计算得出最高的分解层为4，则各分区的冬季降水序列可被分解为4个细节分量 D1、D2、D3和 D4（分别表示 2、4、8 和 16 年的周期性分量），和1个近似分量A4。各分区上的最佳db小波类型和最优分解层由原始降水序列与近似分量序列间的平均相对误差（MRE）与其MK趋势值（MK-Z值）间的相对误差（er）[4-5]这2个指标来确定。通过对指标的计算发现，各db小波及各分解层的MRE值之间的差异不显著，而er值之间的差异较为显著。该现象与Nalley等[4]和Palizdan[5]的研究发现一致，因而采用er值最小的原则选取最佳db小波类型和最优分解层。经过计算分析得出各分区的最佳db小波类型和最优分解层如表3所示。从表3中可以看出：区域DJF2和DJF4的最优分解层是2，最佳db小波类型分别为db8和db7；而区域DJF1、DJF3和DJF5的最优分解层皆为3，但其最佳db小波类型各不相同，分别为db1、db2 和 db10。

表3 各分区的最佳db小波类型和最优分解层

然后，基于已识别的最佳db小波基和最优分解层，从各细节分量和近似分量的Dj+AJ（j=1，……，J）分量组合中，以期识别影响原始降水序列变化趋势的最占优的分量及周期分量。详细地，一是将Dj+AJ分量的SQMK趋势线与原始降水序列的进行对比，以检查Dj+AJ分量与原始降水序列趋势变化的拟合度；二是通过计算原始降水序列与Dj+AJ分量的u(t)值间的均方根误差（RMSE）和相关系数（R），从而选出影响各区域冬季降水变化趋势的最占优的周期分量。一般地，Dj+AJ分量的RMSE值越小，R值越大，表明该Dj+AJ分量与原始降水序列的变化趋势更为匹配，其相应的Dj+AJ分量为影响原始降水序列变化趋势的最占优的分量，而Dj则为最占优的周期分量。

表4给出了各分区的细节分量、近似分量以及Dj+AJ分量与原始降水序列的u(t)值间的RMSE和R，以及各自的MK-Z值。表4表明：湖南省各分区的冬季降水均呈增加趋势但各区存在差异，其中区域DJF3、DJF4和DJF5呈显著的上升趋势。这说明湖南省东南部的冬季降水比西北部具有更快的增长趋势。除了区域DJF4的D2分量之外，其它各分区的细节分量的MK-Z值均未通过显著性检验。然而，各细节分量与近似分量的组合（Dj+AJ）的MK-Z值比单个的细节分量的MK-Z值更具有统计学意义，且其趋势方向与对应的原始降水序列一致，表明近似分量携带了主要的趋势信息。表4中，各分区的Dj+AJ分量的R值均通过了5%的显著性检验，说明其与各自分区的冬季原始降水序列间具有显著的相关性。因此，在识别影响冬季降水变化趋势的最占优的周期分量时，以RMSE值最小为准则。区域DJF1中，D1+A3分量和原始降水序列的MK-Z值更为接近，且RMSE值最小，说明D1+A3分量是影响该区域冬季降水变化趋势的最占优的分量。类似地，D1+A2分量是影响区域DJF2冬季降水变化趋势的最占优的分量。而区域DJF3中，D1+A3分量的RMSE值最小，说明D1+A3分量是最占优的分量。区域DJF4中，D1+A2分量的RMSE值最小，说明D1+A2分量是最占优的分量。类似地，D1+A3分量是影响区域DJF5冬季降水变化趋势的最占优的分量。因而，D1分量是影响湖南省5个子区域冬季降水变化趋势的最占优的周期分量。

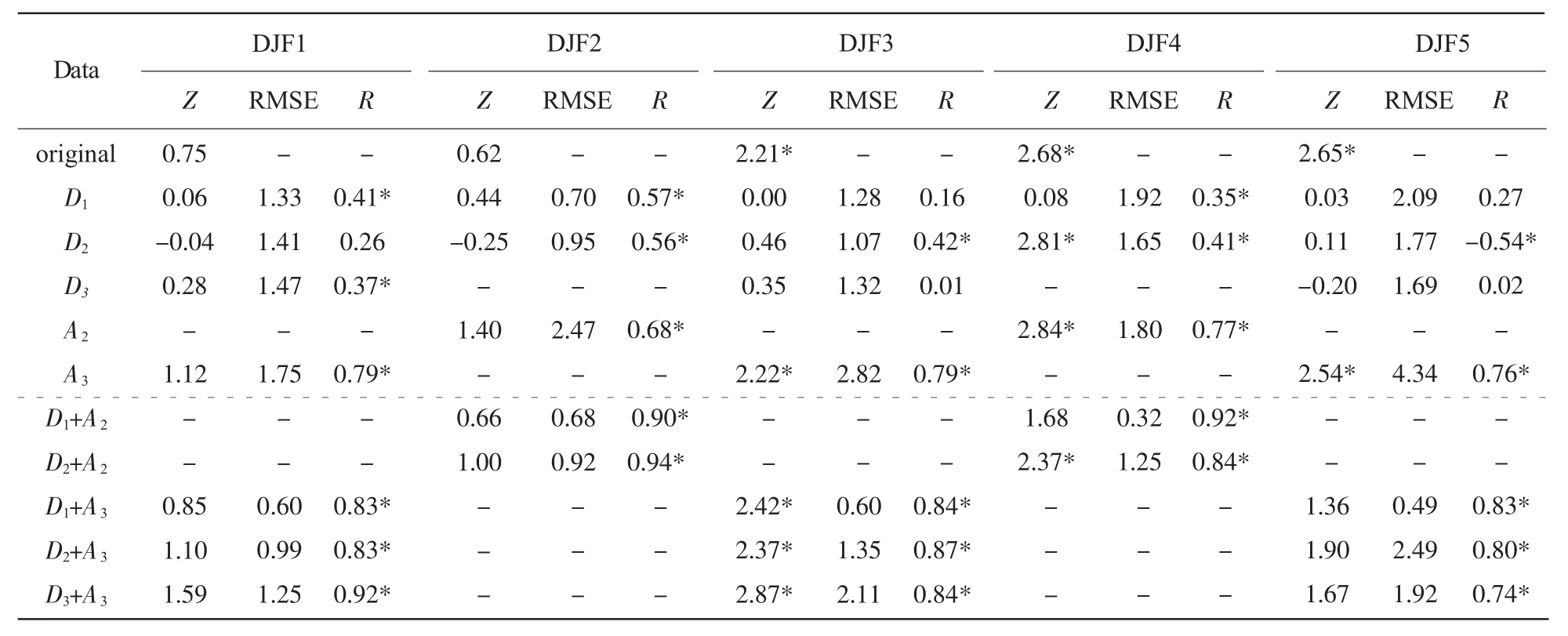
表4 各分区单个分量和不同Dj+AJ分量与原始降水序列u(t)值间的RMSE和R以及各自的MK-Z值

为了更直观地呈现影响各分区冬季降水变化趋势的最占优的周期分量，图6给出了5个分区的原始降水序列和不同Dj+AJ分量的趋势线图。从中可以观察到：在区域DJF1、DJF3和DJF5，冬季降水存在3个周期分量D1+A3、D2+A3和D3+A3，而D1+A3分量的变化趋势线与其原始降水序列的变化趋势线最为匹配，进一步佐证D1+A3分量是影响这些区域冬季降水变化趋势的最占优的分量；而在区域DJF2和DJF4，冬季降水主要存在2个周期分量D1+A2和D2+A2，其中D1+A2分量的变化趋势线与其原始降水序列的变化趋势线更具一致性。因此，D1分量是影响湖南省5个不同子区域冬季降水变化趋势的最占优的周期分量，表明湖南省冬季降水的变化趋势存在准2年的主周期振荡。这与张剑明等[35]得出的湖南省冬季降水有2年左右的特征时间尺度具有一致性，且这种准2年的周期振荡可能与平流层大气环流的准2年周期振荡有关。

5 结 论

根据湖南省89个气象站点1960—2013年的冬季降水观测数据，应用REOF和HCA对湖南省冬季降水进行分区。在分区的基础上，运用离散小波变换与MK和SQMK相结合的方法对各分区的冬季降水序列进行小波多尺度分解，以探究湖南省冬季降水的变化趋势及影响其趋势的最占优的周期分量，得出以下主要结论。

（1）湖南省冬季降水异常变化有3个主要的空间模式：第一模式以湘南地区为降水异常敏感区，并反映出武陵山脉以南和雪峰山脉以北一带的冬季降水与湖南省其它地区具有反位相的变化特征；第二模式的降水异常敏感区位于湘西北地区，并呈现出湘中及湘南的部分地区的冬季降水与湖南省其它地区具有相反变化的特征；第三模式从西北向东南大致呈“正负正”交替分布，湘中地区为其降水异常敏感区，并反映出湖南省冬季降水在中部与南北地区具有反位相的变化特征。

（2）湖南省的冬季降水沿西北向东南可依次划分5个空间上明晰的一致性子区域：湘西北区、湘西-湘北区、湘西南-湘中区、湘南丘陵区和湘南山地区，且每一子区域从西南向东北呈带状分布，而它们的区域平均冬季降水量从西北向东南递增。区域冬季降水序列的趋势分析表明：近54年来，湖南省冬季降水呈增加趋势，其中，湘西南-湘中区、湘南丘陵区和湘南山地区呈显著的增加趋势，而湘西-湘北区和湘西北区呈缓慢的上升趋势。

（3）各子区域的年代际降水变化具有先波动上升后又波动下降的趋势。湖南省各分区的冬季降水在1980年代中期之前均呈波动增加的趋势，但降水均偏少，1980年代中期之后降水趋于偏多，但进入21世纪以来，各区域的降水又由偏多转为偏少。冬季降水的这种年代际变化与东亚季风强度的年代际变化是相关的。

（4）湖南省5个子区域冬季降水的小波多尺度分析表明：在湘西北区、湘西南-湘中区和湘南山地区，D1+A3分量的变化趋势线与原始降水序列的更为匹配；而在湘西-湘北区和湘南丘陵区，D1+A2分量的变化趋势线与原始降水序列的更具有一致性。因而，D1分量是影响湖南省不同区域冬季降水变化趋势的最占优的周期分量，且冬季降水的变化趋势存在准2年的主周期振荡。