利用PCA-kNN方法改进广州市空气质量模式PM2.5预报

汤 静，王春林，谭浩波，邓雪娇，邓 涛

(1.广州市气候与农业气象中心广东广州511430；2.广东省生态气象中心广东广州510640；3.中国气象局广州热带海洋气象研究所／广东省区域数值天气预报重点实验室，广东广州510640)

1 引 言

广州市位于珠江三角洲中心，近年快速的经济发展和城市化进程导致细颗粒物（PM2.5）污染及其引起的大气污染事件（如灰霾[1-3]）日益受到政府和公众的广泛关注。政府制定污染减排应对决策和公众出行均对PM2.5的准确预报提出日益迫切的需求。

预报PM2.5的方法可分为三类：（1）统计方法。通常基于历史观测数据构建自变量与因变量的统计模型用于预报[4-5]，在观测数据足够的情况下比较容易拟合统计模型，但是统计方法难以预测长期和大范围的空气污染，无法预测污染物的成分或含量进而为污染减排提供参考[6-8]。（2）动力方法。基于空气质量数值模式的动力预报能较为完整地反映气象因素、源排放以相关物理化学过程的变化[8-10]。然而，由于排放源、初边界条件、物理化学参数等存在较大不确定性，数值预报的准确性还有待进一步提升[8,11]。（3）统计与动力相结合的方法。空气质量模式的误差主要由随机误差和系统性偏差构成，基于空气质量模式的输出和历史观测数据，应用统计方法订正模式偏差，能有效降低系统性偏差[12-13]。偏差订正过程并不会加深对模型缺陷或性能的了解，或者人为修正它们，但旨在根据空气质量模式或输入数据的内在特征消除潜在的偏差[12]。

目前空气质量模式偏差订正方法主要有：（1）线性回归/模式输出统计[14]（Model Output Statistics，MOS）。Konovalov等[15]基于CHIMERE模式产品、GFS模式数据、PM10观测数据，利用线性回归方法订正模式PM10预报产品，订正结果较模式产品均方根误差降低45%，可决系数 (Coefficient of determination)几乎提高一倍。王开燕等[16]利用MOS方法对珠三角空气质量预报模式预报结果进行订正，降低了预报偏差。（2）滑动平均偏差订正，即在一定的时间段内计算模式与实况的偏差，在当前预报上减去偏差得到订正预报[13]。谢敏等[17]考虑CMAQ模式预报的浓度变化趋势，采用预报日前一天的监测数据订正PM10预报，提高了24 h均值预报的准确度。（3）乘数比例法。Borrego等[12]采用乘数比例和卡尔曼滤波两种方法对BSC-DREAM8b模型PM2.5预报进行订正，订正后的相关系数较原模型提高50%以上。（4）卡尔曼滤波。Kang等[18]采用实时卡尔曼滤波偏差订正方法对NAM-CMAQ模式24 h时效PM2.5预报进行订正，降低了预报误差、提高了相关系数。（5）组合方法。Djalalova等[13]利用历史相似与卡尔曼滤波方法相结合对空气质量数值模式CMAQ PM2.5产品订正后平均绝对误差降低50%～75%，相关系数提高40%～60%。黄思等[19]利用多模式集合和多元线性回归改进北京PM10预报，提高了预报准确率。Lyu等[20]根据模式偏差、模式预报及观测数据的历史数据提出一个偏差订正框架进行预报后处理，降低了空气质量模式CMAQ PM2.5预报的均方根误差。上述不同订正方法效果的差异可能与研究区域不同的自然、社会经济等条件有关[20]，但都能改进原模式的预报效果，反映了引入监测数据对空气质量数值预报模式进行订正的可行性。相较于MOS等方法，机器学习算法处理海量数据更便捷、构建模型更灵活、预报准确性更高[21]，但上述文献中鲜有应用[20]。

本文基于空气质量模式（CMAQ）[11]PM2.5等污染物浓度预报、中尺度天气模式（GRAPESMESO）[22]气象要素预报及广州市环境空气质量监测国控点PM2.5实况数据，提出应用主成分分析方法（Principal Component Analysis，PCA）对数据进行前处理，再结合机器学习算法k近邻[23-24]（k nearest neighbor，kNN）建立逐日滚动偏差订正的方法（PCA-kNN），改进广州市PM2.5客观预报能力，并验证利用机器学习算法订正空气质量模式PM2.5预报的可行性。

2 数据及方法

2.1 数 据

本文采用的中尺度天气模式是我国自主研发的 GRAPES-MESO (Global and Regional Assimilation and Prediction Enhanced System-Meso-Scale)[22]模式。GRAPES-MESO采用三维变分同化方法，半隐式-半拉格朗日差分方案和全可压/非静力平衡动力框架，可自由组合的、优化的物理过程参数化方案，是全球、区域一体化的同化与预报系统[22]。空气质量模式采用中国气象局广州热带海洋气象研究所搭建的华南区域空气质量数值预报模式系统[11]，以GRAPES-MESO作为气象场驱动CMAQ，采用高时空分辨率的三重嵌套模式域，分辨率分别为27 km、9 km、3 km，模拟采用三重单向嵌套网格，为泛珠三角区域、特别是区域重点城市提供 PM2.5、PM10、O3、NO2、SO2、CO等6种污染物浓度的0～96 h逐小时预报产品。

本文用到2017年上半年广州市11站的相关数据如下：（1）CMAQ模式20时（北京时间，下同）起报 1～72 h 逐时 PM2.5、PM10、O3、NO2、SO2、CO等污染物浓度预报数据；（2）GRAPES-MESO模式20时起报1～72 h逐时气温、相对湿度、气压、降水、风速、位势高度、垂直速度（含地面、1 000 hPa、925 hPa、850 hPa、700 hPa、500 hPa 等层次）等气象要素数据；（3）逐时PM2.5浓度实况数据。

2.2 方 法

2.2.1 主成分分析

主成分分析(PCA)最初是由Pearson(1901年)在非随机变量的讨论中介绍的，后来由Hotelling扩展到随机变量[25-27]。PCA的目的是将相关性较强的多维变量转化为彼此不相关的新变量。PCA方法的优点在于：（1）仅以方差衡量信息量，不受数据集以外的因素影响；（2）各主成分之间正交，可消除原始数据成分间相互影响的因素。在实际应用中，经过PCA处理后，前几个主成分已经包含了大部分原始变量的变异信息，选取累计贡献率达到90%的主成分进行分析，达到降维的目的。本文利用PCA方法对数据进行前处理。

2.2.2 k近邻

k近邻(kNN)是一种常用的监督学习算法[24]。kNN方法在水文学研究中得到广泛应用[28-29]，后被Wu等[30]应用到降尺度季节天气预报上去。kNN的工作机制是：给定测试样本，基于某种距离度量找出训练集中与其最靠近的k个训练样本，然后基于这k个“邻居”的信息来进行预测[24]。在回归任务中一般使用平均法，即将这k个样本标记的平均值作为预测结果，也可以基于距离远近进行加权平均或加权投票，距离越近的样本权重越大[24]。kNN算法的优点是精度高、对异常值不敏感、无数据输入假定，缺点是计算复杂度高、空间复杂度高[24]。

kNN算法假定所有的实例对应于n维欧氏空间An中的点。把任意实例x表示为特征向量：a1(x)，a2(x)，……，an(x)，其中 ar(x)表示实例 x 的第 r个属性值。那么两个实例xi和xj之间的距离定义为 d(xi，xj)，其中：

2.2.3 评估指标

评估CMAQ模式PM2.5产品以及PCA-kNN方法订正效果的指标主要有相关系数（Correlation coefficient，r）、均方根误差 （Root Mean Square Error，RMSE）和平均偏差（Mean Bias，MB）。计算公式分别如下：

其中，N为样本数量，Mi为预报值，Oi为观测值。此外，根据《环境空气质量指数（AQI）技术规定（试行）》(HJ633-2012)[31]规定的PM2.5浓度限值，把PM2.5浓度分为六个等级，对不同等级分别计算TS评分[32]。

其中，对于某个等级，NA是预报正确的次数，NB是空报次数，NC是漏报次数。

2.2.4 PCA-kNN方法

PCA-kNN方法流程如下：（1）样本数据收集。例如起报日期为t，最佳历史数据天数为d，则下载广州市各站点t-d至t日CMAQ 20时起报的1～72h逐时污染物浓度预报数据、GRAPES-MESO 20时起报的1～72 h逐时气象要素数据以及起报时间（t日20时）以前相应时次的PM2.5观测数据。（2）数据质量控制。去掉所得数据里的缺测以及异常值。（3）标准化及PCA处理。以CMAQ和GRAPES-MESO模式预报数据为自变量，PM2.5观测数据为因变量。根据应用kNN等机器学习算法的需要，对自变量进行标准化处理（即原数据减去其平均值，再除以标准偏差）。把标准化后的结果进行PCA处理，选择累计贡献率达到90%的主成分。（4）将训练数据分成训练集、验证集、测试集。将t-d至t-1日的历史数据作为训练数据。将训练数据按时次随机排列，选择70%的数据作为训练集，20%的数据作为验证集，10%的数据作为测试集。（5）训练kNN模型，参数优化。以自变量和因变量为输入，训练kNN回归模型。kNN回归模型的主要参数是邻近样本个数即k值，采用交叉验证和网格搜索[33]，选择验证误差和测试误差最小的k值。（6）基于待订正的模式产品得出订正预报。将t日起报的模式数据作为输入，以上述最佳的k值作为参数进行kNN回归预报，得到t日起报的订正预报。

PCA-kNN方法主要基于scikit-learn[33]实现，scikit-learn是PYTHON语言环境下十分流行的开源机器学习算法库，它集成了当下最先进的机器学习算法，并提供了易用、高效、统一的API接口。

2.2.5 参数试验

订正方法的参数影响订正效果及训练所耗费的时间，本文通过参数试验来选择PCA-kNN方法的参数方案（表1）。试验数据范围及时间：广州市2017年1月共31天。试验方案的区别主要是训练数据的来源、时效两方面，例如CG72方案采用了1～72 h的历史CMAQ和GRAPES-MESO全部预报要素作为自变量，相应时次的PM2.5观测实况作为因变量，训练PCA-kNN模型后基于待订正的CMAQ和GRAPES-MESO预报（此时的模式产品无相应时次PM2.5观测实况）得到1～72 h订正预报。相比CG72方案，G_multi在训练时分为3个部分，而且训练数据中去掉了CMAQ模式产品。

试验过程：根据不同的试验方案获取相应历史数据训练PCA-kNN模型，基于待订正的模式预报产品利用PCA-kNN模型分别对各站点进行1～72 h逐时订正预报，分1～3天时效计算各站点逐日预报，求平均得到相应时效的广州市逐日预报。例如1月1日20时起报的广州市第1天日平均PM2.5数据是由1月1日20时起报的11个站点的第1天预报求平均而得到。选取1～31天历史数据进行建模[8]，计算相关系数、均方根误差、平均偏差，综合考虑上述指标选择最佳历史天数。

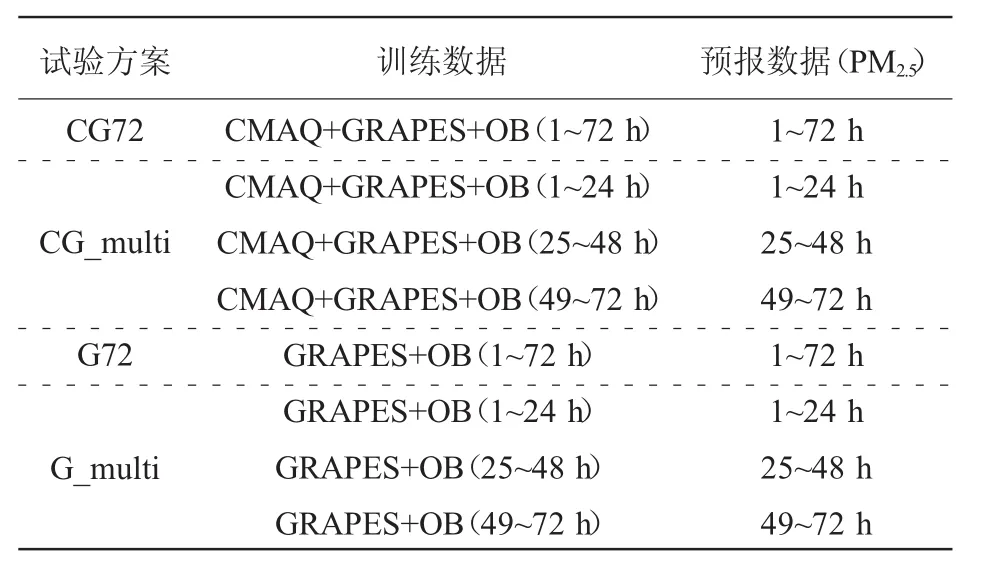
表1 PCA-kNN训练样本参数试验设置

以试验方案CG72为例，2017年1月不同历史数据天数24 h订正预报效果变化如图1所示，相关系数、均方根误差、平均偏差分别在0.60～0.74 μg/m3、21.9～27.2 μg/m3、-1.0～6.7 μg/m3之间。当历史数据天数为1时订正预报与实况的相关系数最高（0.74），较试验平均值（0.64）提高约16%；均方根误差最低（21.9 μg/m3），较试验平均值（24.8 μg/m3）降低约12%；平均偏差为-0.9 μg/m3，较试验平均值（2.8 μg/m3）更接近 0。因此，CG72方案24 h时效最佳历史数据天数为1。同理，对不同方案试验结果选择相关系数最大、均方根误差最低、平均偏差接近0的历史数据天数作为最佳参数得到表2所示结果。

如表2所示，24 h时效，试验效果CG_multi＞G_multi＞CG72＞G72＞CMAQ；48 h 时效，试验效果G_multi＞ CG_multi＞CG72≈G72＞CMAQ；72 h 时效，试验效果 CG72≈G72＞G_multi≈CG_multi＞CMAQ。上述结果表明CMAQ在24 h时效内对提高订正效果的贡献较大，之后逐渐降低。因此把基于CMAQ和GRAPES的24 h订正结果与仅考虑GRAPES的48 h、72 h结果相结合，作为最终订正预报以提高订正效果，由此得出CG_hybrid方案，设置如下（表3）。

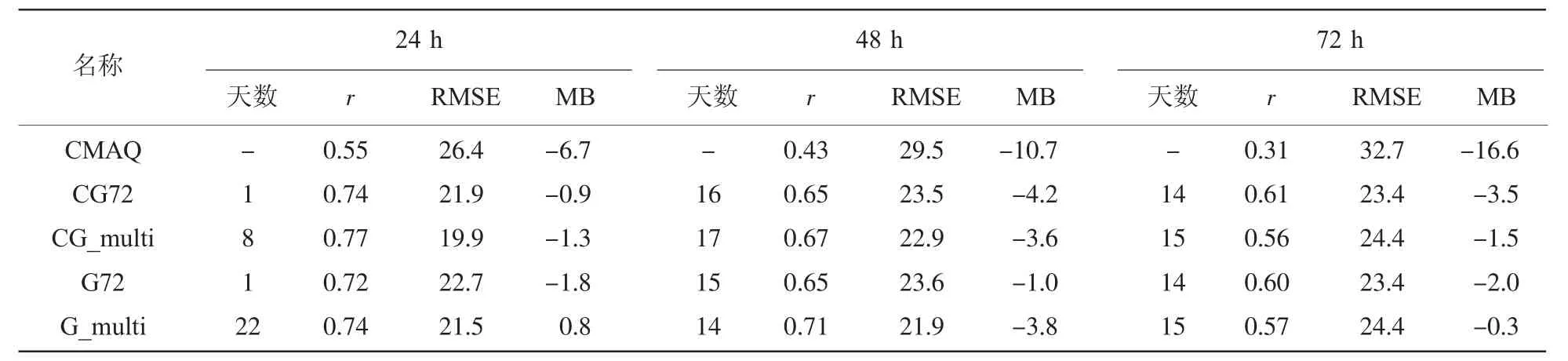
表2 PCA-kNN训练样本试验结果

表3 PCA-kNN CG_hybrid参数方案设置

3 效果评估

3.1 整体评估

采用CG_hybrid参数方案，对广州市2017年上半年进行PCA-kNN PM2.5订正预报，把广州市11个站作为整体进行评估,表明PCA-kNN订正方法能有效提高PM2.5日均值预报效果（表4）。与CMAQ PM2.5产品相比，第1～3天相关系数分别提高20%、15%、29%，均方根误差分别降低17%、16%、20%，平均偏差更接近0。

在TS评分方面，随着PM2.5等级增加，PCA-kNN订正和CMAQ的TS评分呈下降趋势（图 2）。PM2.5等级为一级时（PM2.5≤35 μg/m3），PCA-kNN订正和CMAQ TS评分相差不大，在二级 （35 μg/m3＜ PM2.5≤75 μg/m3） 至 三 级（75 μg/m3＜PM2.5≤115 μg/m3） 时各时效的 PCA-kNN订正TS评分明显高于CMAQ。在PM2.5等级为四级（115 μg/m3＜PM2.5≤150 μg/m3）及以上时，两者TS评分均为0，一方面实况在四级及以上的天数少，另一方面PCA-kNN订正和CMAQ模式对PM2.5重污染过程的预报能力还有待加强。

表4 广州市2017年上半年CMAQ、PCA-kNN订正PM2.5效果评估

逐小时评估方面（图 3），PCA-kNN订正、CMAQ 1～72 h预报的相关系数分别在0.31～0.79与 0.25～0.55之间，平均偏差分别在-2.5～2.3 μg/m3与-15.3～3.6 μg/m3之间，均方根误差分别在 16.4～28.1 μg/m3与 21.8～30.4 μg/m3之 间 。1～15 h的PCA-kNN订正的相关系数较CMAQ提高明显，15 h之后两者相近，两者的相关系数随着时效的增长而降低。PCA-kNN订正1～72 h时效的平均偏差较CMAQ接近0，1～17 h的均方根误差较CMAQ降低明显，17 h之后两者相近。CMAQ均方根误差呈一定的周期性，夜间高于白天，可能是由于模式对夜间边界层气象要素模拟能力有限[34]。

3.2 分站点评估

对广州市11站分别进行1～3天时效CMAQ预报、PCA-kNN订正的PM2.5日均值预报效果评估，结果表明各时效的PCA-kNN订正效果整体上优于CMAQ预报（图4）。

以24 h时效为例，分析如下：（1）平均偏差方面：CMAQ 24 h预报平均偏差范围在-6.7～1.9 μg/m3（图5a），有9个站较实况偏低，表明CMAQ预报整体偏低，原因可能是GRAPES-MESO地面风速模拟偏大[32,35]，但2个站略有偏高，原因可能是CMAQ模式采用的平均源排放清单难以精细、客观描述预报区域不同尺度污染源强度的时空变化[36]，而城区排放面源对这2个站点实际排放源有所高估。PCA-kNN订正平均偏差范围在-4.2～2.9 μg/m3（图5b），有6个站较实况偏低，5个站偏高。从PCA-kNN订正与CMAQ预报平均偏差的绝对值之差来看（图5c），PCA-kNN订正的平均偏差较CMAQ以降低为主（更接近0）。（2）均方根误差方面：CMAQ 24 h预报均方根误差范围在14.2～22.0 μg/m3（图6a），PCA-kNN订正均方根误差范围在12.8～16.8 μg/m3（图6b），PCA-kNN订正与CMAQ预报均方根误差之差范围在-6.4～2.2 μg/m3（图6c），PCA-kNN订正的均方根误差较CMAQ以减小为主。（3）相关系数方面：CMAQ 24 h预报相关系数范围在 0.54～0.69（图 7a），PCA-kNN订正相关系数范围在0.61～0.79（图7b），PCA-kNN订正与CMAQ预报相关系数之差范围在-0.07～0.24（图7c），PCA-kNN订正的相关系数较CMAQ以提高为主。Lyu等[20]在评估偏差订正效果时发现并非所有地区的订正结果都能优于原模式，广州市11站中有10站相对CMAQ预报有所改进（图4），仅1353A站的均方根误差较CMAQ高出2.2 μg/m3，相关系数较CMAQ降低0.07，这可能与观测资料的质量有关。例如1353A站的PM2.5观测数据有效性（有效样本/总样本）为98.4%，低于各站平均值（99.2%）。

3.3 案例分析

2017年上半年CMAQ预报、PCA-kNN订正24 h的PM2.5日均值逐日偏差及相应日期的地面平均风速、降水量如图8所示。统计2017年上半年中偏差绝对值大于10 μg/m3的天数，CMAQ预报、PCA-kNN订正分别为75、58天，两者的偏差绝对值同时大于10 μg/m3的情况有29天（其中有17天平均风速小于1.5 m/s，有16天降水为0 mm）。以2017年1月3—6日为例，广州出现一次PM2.5污染过程（表5），其中1月5日PM2.5达到144.9 μg/m3。1月 5日 20时地面天气图（图 9a）表明广州受均压场控制，等压线稀疏，地面风速小，无降水，500 hPa天气图（图9b）表明广州位于高压后部，盛行下沉气流，总体上大气扩散条件不利。从表5看到，整个污染过程中无降水，模式降水量预报正确；实际地面风速在1.5 m/s以下，但模式预报风速较实况偏高。CMAQ预报及PCA-kNN订正结果在3—5日较PM2.5实况均偏小，但PCA-kNN订正结果更接近实况；1月6日CMAQ预报较实况偏小，PCA-kNN订正较实况偏大。CMAQ预报持续偏小原因之一可能是GRAPES-MESO模式的预报风速较实际风速偏大[32,35]，而PCA-kNN订正能基于历史预报数据与实况修正CMAQ预报，从而在1月3—5日偏差相对CMAQ较小，但在1月6日污染过程趋于结束时，由于历史数据PM2.5浓度高而导致1月6日的订正预报偏高。

表5 2017年1月3—6日广州市PM2.5污染过程分析

4 结论与讨论

基于空气质量模式（CMAQ）预报产品、中尺度天气模式（GRAPES-MESO）预报产品和PM2.5观测实况，提出了结合主成分分析和机器学习算法k近邻的空气质量模式PM2.5预报逐日滚动订正算法（PCA-kNN）。以广州市11站作为整体评估PM2.5日均值预报效果，PCA-kNN订正预报与CMAQ PM2.5产品相比，在第1～3天预报时效上相关系数分别提高20%、15%、29%，均方根误差分别降低17%、16%、20%；对广州市11站分站点评估表明，各时效的PCA-kNN订正效果整体上优于CMAQ预报。这与前人采用MOS订正[16]等方法得到的结论一致。值得注意的是，随着近年CMAQ模式参数、排放源数据和后处理技术的不断改进[11]，基于常规统计方法的偏差订正效果提升有限，本文提出的PCA-kNN可作为一种有效的手段改进广州市空气质量模式PM2.5预报，反映了应用机器学习算法订正空气质量模式PM2.5预报的可行性，对其他地区、其他污染物客观预报研究具有借鉴意义。然而，相比文献[12-13,15]中的订正效果，从相关系数提升或均方根误差降低比例来看，PCA-kNN方法在广州市对CMAQ预报的订正提升程度较小，其差异可能与研究区域不同的自然、社会经济等条件[20]以及被订正模式的预报能力有关[8]。

模式产品偏差订正效果通常随着预报时效增加而下降[8]。总体来看，在1～72 h时效内，PCA-kNN订正预报与实况的相关系数与CMAQ预报相比有所提高，均方根误差有所减小。PCA-kNN订正效果在1～24 h时效内比较显著，25 h之后逐渐降低，如何有效提升25 h以上预报能力值得进一步探讨。

广州市PM2.5污染过程个例分析表明，污染过程中PCA-kNN订正较CMAQ预报更接近实况，能有效提高预报效果，但PCA-kNN订正和CMAQ都没有预报出此次过程的开始及结束，反映了订正效果与模式自身预报能力有关[8,12]。另外，本文采用的PCA-kNN方法参数是基于广州市2017年1月数据提出的，在更大时空范围内进行偏差订正的有效性需要进一步研究。