动基站时差探测系统导引头一维搜索问题研究*

董爱,夏芒,卓志敏,李陟

(1.北京电子工程总体研究所，北京 100854；2.中国航天科工集团有限公司 第二研究院，北京 100854)

0引言

隐身飞机已成为空防安全面临的重大现实威胁。目前，美国在关岛基地部署了B-2隐身轰炸机、F-22A隐身战斗机等，并在日本冲绳嘉守纳基地、韩国群山空军基地不定期部署F-22A。此外，许多国家和地区都在积极通过参与研制或购置方式，谋求装备隐身飞机。先进空袭装备隐身化设计已成发展趋势并将常态化。2030-2050年间，隐身目标将成为空袭体系的骨干和主体，是空袭体系实施并强化防区外、强渗透、穿越式等攻击样式的核心和支柱，对防空体系构成严重潜在威胁。

隐身目标低可探测性使得防空导弹拦截空域大大缩减。为形成对隐身目标的中远程拦截能力，国内外在频域、能量域、空域、新型反隐身探测制导技术等方面陆续开展了对抗隐身目标技术的研究。隐身目标难以实现全频段隐身，使得频域反隐身作战成为可能。低频雷达通常工作在目标隐身频段之外，相对于厘米波雷达具有更好的反隐身优势[1-3]，因此采用低频雷达制导又重新受到了各军事大国的重视。如俄罗斯“天空-M”雷达，作为S-400防空导弹系统的雷达，由米波雷达、分米波雷达、厘米波雷达组成，采用综合探测原则，利用米波雷达探测出入侵的隐形战机正面反射信号；美国新一代宙斯盾驱逐舰上配备的低频相控阵雷达，对0.01 m2的目标探测距离可达786 km。

低频雷达由于波束宽，测角精度低，通常用于预警探测，而很少用来对导弹进行制导。低频制导雷达用于远距离导弹制导的一个难点是实现向末制导导引头的交班，一方面可以提高低频制导雷达的精度[4-5]，一方面可以提高导引头能力[6-8]。提高低频制导雷达精度的研究主要集中在2个方面：一是在不改变制导体制的情况下采用新的技术提高低频制导雷达本身探测精度，如米波超分辨技术，采用该技术后仍需要导引头二维搜索；二是开发新体制[9-11]，如冲激雷达，技术成熟度有待提高。受限于弹径约束，进一步增大导引头威力存在工程实现问题。导引头采用搜索工作方式[12-16]是放宽对地面制导雷达精度要求的一条可选途径，在搜索时间可以接收的情况下可以作为一种备选工作模式。

基于以上考虑，本文提出了动基站时差探测系统，采用地面单站低频制导雷达配合弹上时差测量设备提高低频制导雷达的俯仰向测量精度，完成角度预置。导引头沿地面雷达高精度斜距测量球面、弹上时差测量设备高精度时差测量椭球面的交线完成一维搜索，避免低频制导雷达测角精度差给导弹制导带来的影响。该方法综合利用频域、空域等反隐身技术途径，可实现设备优势互补，为中远程拦截隐身目标作战提供可行途径。

1 动基站时差探测系统工作原理

动基站时差探测系统包括地面低频雷达和弹上低频时差测量设备(图1)。地面低频雷达测量目标斜距Rt、目标方位角βt、目标俯仰角εt、导弹斜距Rm；弹上低频时差测量设备为动基站，测量地面雷达照射直波和目标反射回波的距离差RΔ。

图1 动基站时差探测系统示意图Fig.1 Moving based station time-of-arrival detection system

2 动基站时差探测系统目标定位精度分析

2.1 动基站时差探测系统目标定位方法

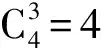
方法1：雷达测目标斜距+动基站测时差+雷达测目标方位角；

方法2：雷达测目标斜距+动基站测时差+雷达测目标俯仰角；

方法3：雷达测目标斜距+动基站测时差+雷达测目标方位角+雷达测目标俯仰角。

(1)目标定位方法1

该方法中目标三维坐标由式(1)得到

(1)

式中：Rmt为弹目距离;(xm,ym,zm)为导弹的位置，由弹上惯导测量设备得到

(2)

(3)

(2)目标定位方法2

该方法中目标三维坐标为

(4)

(3)目标定位方法3

该方法中目标三维坐标为

(5)

2.2 动基站时差探测系统凝视交班分析

仿真条件选取：导引头作用距离为8 km，目标飞行高度10 km，交班时弹目视线角15°，误差项取值如表1，仅考虑随机误差。

仿真结果分析：以上3种方法的交班误差比较如图2所示。

从图2中分析，当目标距离大于80 km时，无论哪种定位算法，都很难满足交班需求。由于低频雷达测角误差大，导致交班俯仰角和交班方位角的误差都很大，导引头必须进行两维搜索才能完成交班，交班时间过长会导致末制导工作时间太短，制导控制系统无法消除误差，最终脱靶。

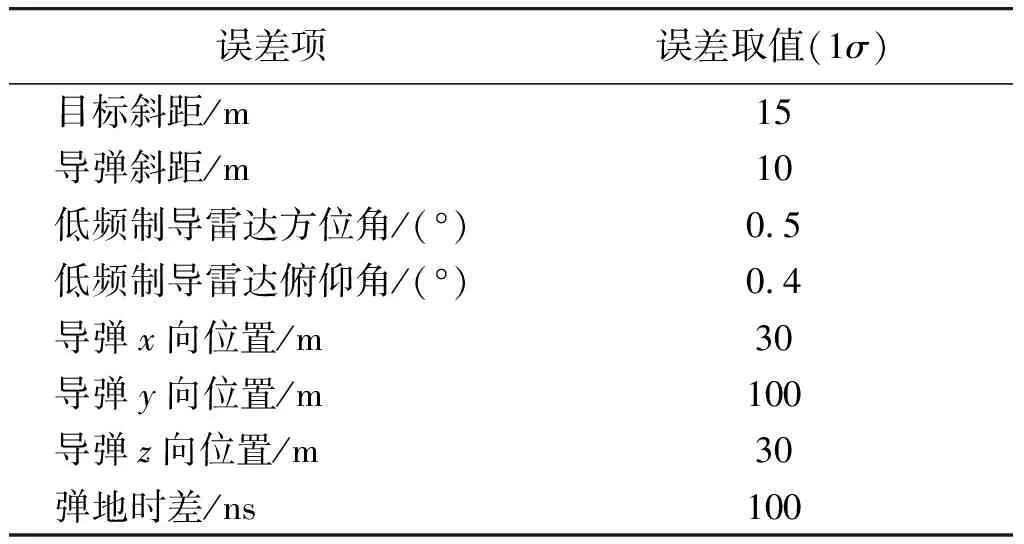
表1 仿真误差项取值Table 1 Value of error terms

图2 3种方法下的交班角误差Fig.2 Error angle of handover on three methods

另外,在导弹定位精度一定的情况下，3种目标定位方法的各误差占比分析情况如图3所示。

由图3中可以看到,目标斜距误差和动基站时差误差对总的交班误差贡献很小，3种方法中主要误差来源分别是方位角误差、俯仰角误差、方位角误差，占了总误差的98%以上。因此,影响目标定位精度的主要是雷达的测角误差，要提高精度实现中末制导交班，则在交班时应尽量避免采用雷达的测角信息。

图3 3种方法下交班误差中各误差占比Fig.3 Duty ratio of handover error angle of three methods

3 时差探测系统导引头一维搜索方法

为解决动基站时差探测系统用于导弹制导的问题，本文提出采用两维高精度距离测量信息配合导引头一维角度搜索的方案，综合得到目标角度信息，有效解决交班问题。时差探测系统导引头一维搜索基本思想是首先由相对高精度的目标测量信息完成导引头角度预置，沿地面雷达高精度斜距测量球面、弹上时差测量设备高精度时差测量椭球面的交线完成搜索，减少搜索波位及时间，增大末制导可用时间，确保对目标的拦截。

3.1 坐标系定义及转换关系

综合利用地面雷达斜距测量信息和弹上时差测量设备时差测量信息，需要先建立两维信息之间的联系。为此先建立两维信息之间的转换关系，地面雷达斜距测量信息是在雷达北天东坐标系下的信息，弹上时差测量设备时差测量信息是在弹体坐标系下的信息。2坐标系定义如下：

雷达北天东坐标系：

代号：Ogxgygzg

原点Og——取在相控阵雷达配置点；

Ogxg轴——指向正北；

Ogyg轴——指向天顶；

Ogzg轴——与Ogxg和Ogyg构成右手坐标系。

弹体坐标系：

代号：O1x1y1z1

原点O1——设在导弹质心；

O1x1轴——沿导弹纵轴指向头部为正；

O1y1轴——在导弹纵对称平面内，垂直O1x1轴，向上为正；

O1z1轴——垂直于O1x1y1平面，其方向按右手定则确定。

雷达北天东坐标系Ogxgygzg到弹体坐标系O1x1y1z1的转换：首先进行坐标原点的平移，然后是逐次的坐标轴转动，先绕y轴转ψ角，再绕新的z轴转ϑ角，再绕新x轴转γ角来实现的,如图4所示。ψ，ϑ，γ相应称为偏航角、俯仰角和滚动角，变换矩阵为

(6)

图4 雷达北天东坐标系与弹体坐标系间的转换Fig.4 Coordinate transformation between radar north sky east and projectile

3.2 导引头一维搜索原理

当前能通过测量得到的两维高精度信息分别是雷达北天东坐标系下的目标斜距Rt和弹体坐标系下的目标斜距Rmt，有如下关系：

(7)

(8)

式中：xtg，ytg，ztg为目标在雷达北天东坐标系下的位置；x1，y1，z1为目标在弹体坐标系下的位置，二者之间存在如下转换关系：

(9)

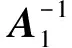
(10)

由于A1是正交矩阵，因此有

(11)

将式(11)式代入(10)式，得到

(12)

将式(12)代入式(10)，得到

(13)

可得到关于x1，y1，z1的二次方程组

(14)

求解该方程组可消去x1，得到y1和z1的关系式

z1=f(y1)，

(15)

即

(16)

式中:

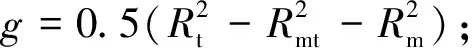
只要假设一个y1就可以求出z1，于是在弹体坐标系中，目标的方位角和俯仰角为

ε1=arcsin(y1/Rmt)，

(17)

(18)

导引头搜索时按此角度预置，对不同的y1，可求出一组相对应的(ε1，β1)来搜索，就可以不用两维搜索。

3.3 导引头一维搜索方法

在确定采用一维搜索交班后，具体搜索策略的设计成为导引头设计的关键。导引头搜索策略中，有2个关键的问题需要解决，一是确定搜索波位数，二是确定具体搜索波位和搜索顺序。

确定导引头搜索波位数一般应遵循以下原则：一是要全面覆盖目标的可能位置；二是尽可能地减少搜索波位数；三是考虑导引头波束波位的重叠覆盖。为了全面覆盖目标可能的位置，需要首先分析目标可能散布的位置。通常情况下，目标散布情况可以看成是一个正态分布的随机变量，设其均值为m，方差为σ，则目标分布的概率密度函数为

(19)

导引头截获目标的概率可以表示为

(20)

式中：Pd为截获概率；Ω为目标有效搜索覆盖区域。

通常情况下，导引头交班过程中会将雷达探测的结果经过转换后送到弹上，使导引头波束直接指向所测得的目标位置方向，可以认为公式中随机变量均值m=0，要保证可靠交班，根据6σ原则，只需要搜索区域覆盖±3σ即可保证99.75%的交班概率。

在导引头一维搜索情况下，目标俯仰角和方位角存在着一一对应的关系，只需考虑其中一个方向上的搜索即可。为此首先分析一维搜索时目标空间散布情况。由3.2节可知，在导弹弹体坐标系下，目标散布为一条由式(21)确定的平面轨迹：

z1=f1(y1)或者y1=f2(z1).

(21)

由2.2节中分析可以看到，目标定位方法3所得到的定位精度最高，因此可以将方法3解算的目标位置作为目标位置中心，在计算目标位置时，同时计算目标测量y向和z向误差，通常取y1，z1中误差变化范围较大的作为变量。为简化分析，后面的分析中以y1作为变量，当以z1作为变量时，方法相同。

根据波束全覆盖原则，求出目标散布轨迹长度为

(22)

假设采用N个搜索波束来均匀覆盖该轨迹，并假设导引头波束在目标所在平面投下圆形投影，其半径为Rb，则有Rb=θ/2·Rmt，θ为波束宽度。

由基本几何知识可知，每个波束的责任覆盖范围不超过投影圆的直径，可以保证目标全覆盖，因此有如下关系：

s=l/N<2Rb.

(23)

得到N>l/2Rb，又因为N为正整数，进一步有搜索波位数为N=Ceil(l/2Rb)，其中Ceil为向上取整函数。若考虑到一定的余量，相邻的波束之间保证一定的重叠覆盖率，则搜索波位数为N=Ceil(l/2kRb)，其中k为与重叠覆盖率相关的系数，一般为0～1之间的小数。

当确定了搜索波位数后，下一步即是确定具体搜索波位和搜索顺序。搜索波位中心在式(21)确定的轨迹线上，相应的波束中心由式(24)确定：

(24)

式中：y0为目标散布轨迹起点，一般为负的目标测量误差最大值；yi即是第i个波束中心值。

导引头波束宽度8°时采用一维搜索交班的搜索方案，只需4次搜索即可保证目标全覆盖，如图5所示。

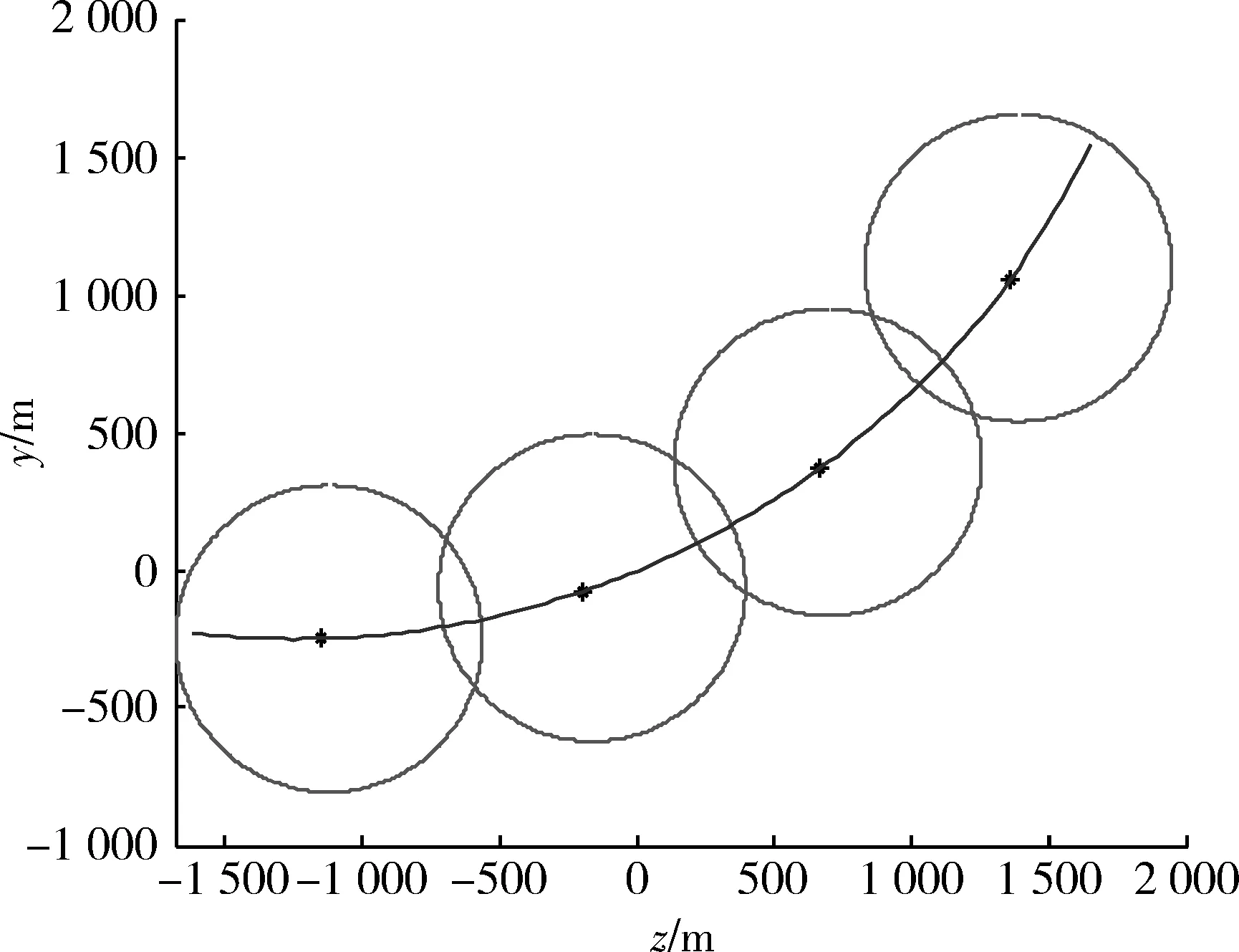
图5 导引头一维搜索方案Fig.5 One dimensional search scheme of seeker

确定波位后，导引头的波位搜索顺序也是要考虑的问题。按照目标正态分布来看，通常在计算的目标中心位置截获目标的概率是最大的，为了快速截获目标，应首先搜索目标中心位置，再搜索目标中心两侧位置。在实际工程实践中，常平架导引头采用机械扫描方式，存在惯性，天线的来回摆动会给控制系统带来相当大的困难，且搜索时间开销也存在一定权衡优化的问题，需与波位驻留时间以及扫描速度结合考虑。而相控阵导引头通过电子扫描，不存在惯性问题，切换速度也快，可以按照概率分布从中心到两侧的顺序扫描。

实际应用时，导引头搜索方法应综合考虑导引头威力、导引头搜索时间、导弹纠偏能力等多方面因素，以确保对目标的高概率截获。

4 结束语

动基站时差探测系统综合运用了地面雷达和弹上时差测量设备的测量信息，最大程度地利用了高精度距离信息，并通过综合低精确的角度信息确定导引头搜索范围，配合导引头一维搜索可以最小的代价实现导弹中末制导交班。该交班方案充分发挥了低频雷达对隐身目标的探测优势和导引头的搜索能力，在确保可靠交班的同时，减少了目标截获时间，为末制导留出可用时间，确保对目标的高概率拦截。该方法技术可行性高，具有一定的工程研制参考价值。