使用状态方程计算天然气焦耳-汤姆逊系数

苑伟民，王 辉，陈学焰，王 乐，雷江开，张晓辉，陈 力

1.中石化北海液化天然气有限责任公司，广西北海 536000

2.中国石油华北油田公司技术监督检验处，河北仁丘 062552

1 焦耳-汤姆逊系数及其基本关联式

高压流体经节流膨胀后，由于压力变化而引起温度的变化，被称为节流效应或者焦耳-汤姆逊（Joule-Thomson）效应[1]。节流膨胀可近似看作敞开系统稳流过程，并且是绝热又无轴功，如略去动能、位能变化，焓差为零，是恒焓过程。节流膨胀时，微小的压力变化引起温度变化的关系称为微分节流效应系数或焦耳-汤姆逊（Joule-Thomson）效应系数[2]，以μJ来表示，它代表在等焓的情况下节流过程中温度随压力的变化率。

式中：μJ为焦耳-汤姆逊系数，K/kPa；p为系统压力，kPa；T为系统温度，K；H为气体的焓，J/mol。由热力学关系式：

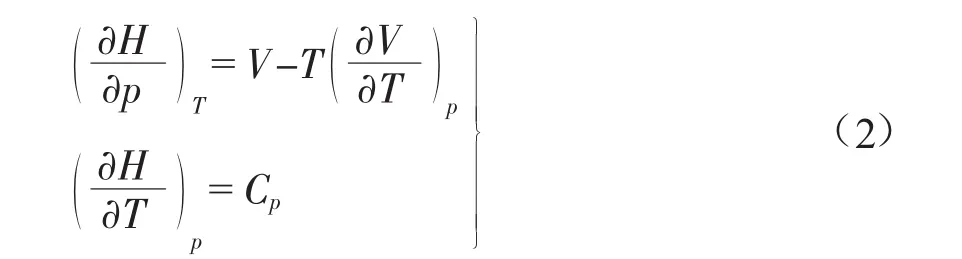
式中：V为气体的摩尔体积，m3/kmol；Cp为气体的定压比热容，J/（mol·K）。

对于实际气体：

当dH=0，可得：

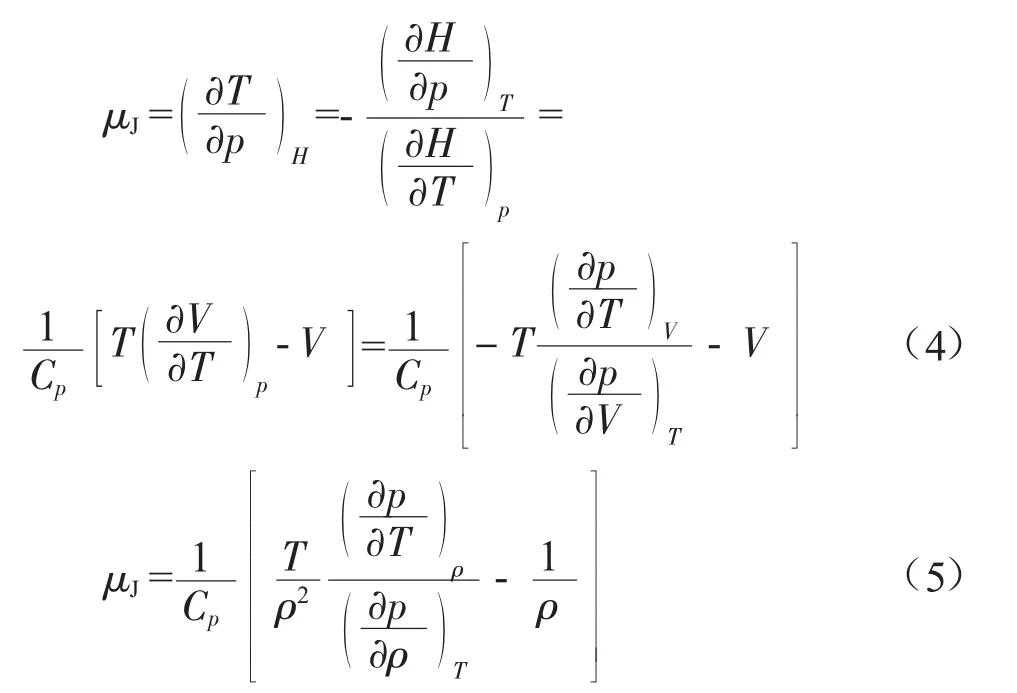
式中：ρ为气体摩尔密度，kmol/m3。

焦耳-汤姆逊系数中的偏微分项可通过实际状态方程来求解，常用的气体状态方程有Redlich-Kwong（RK）、Soave-Redlich-Kwong（SRK）、Peng-Robinson（PR）、Benedict-Webb-Rubin-Starling（BWRS）、Lee-Kesler-Plocker（LKP） 方程。本文将一一进行求解各状态方案下的焦耳-汤姆逊系数。

2 Redlich-Kwong（RK）状态方程

2.1 方程的形式及混合规则

Redlich和Kwong于1949年提出的两参数状态方程原始形式如下[3]：

采用Soave给定的混合规则[4]，a和b的系数采用修正过的数值[5-15]：

其中，a和b的混合规则见下式：

式中：Tci为临界温度，K；yi为纯组分i的摩尔分数；n为组分总数。

2.2 焦耳-汤姆逊系数

将式 （9） ～ （10） 代入式 （4） 可得：

3 Soave-Redlich-Kwong（SRK）状态方程

3.1 方程的形式及混合规则

1972年Soave提出了改进的RK状态方程（简称SRK方程）[4]，将RK方程中a/T0.5项改用较具普遍意义的温度函数α（T）来代替，a和b的系数采用修正过的数值[6-15]，即：

α是与气体温度和偏心因子ω有关的无因次因子，α按下式计算：

对于混合气体，除了考虑各组分i的常数ai和摩尔分数yi外，为了改进对非烃-烃体系的预测，Soave模型在参数a的混合规则中引入经验校正因子Kij，混合规则如下式：

式中：Tri为对比温度，Tri=T/Tci，无量纲；i、j代表流体组成，n为流体组分总数，yi、yj为纯组分的摩尔分数。

3.2 焦耳-汤姆逊系数

4 Peng-Robinson（PR）状态方程

4.1 方程的形式及混合规则

1976年，Peng-Robinson在SRK模型基础上进行了修正，提出了PR状态方程[16]：

混合规则同式（16）。

4.2 焦耳-汤姆逊系数

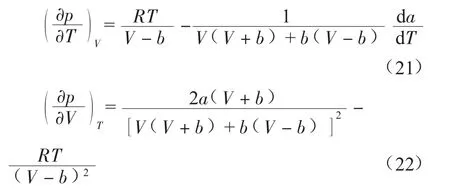
将式（21）、（22） 代入式（4） 可得：

5 SRK方程和PR方程中的温度导数

SRK方程和PR方程中的温度导数形式一致，温度的一阶导数da/dT和Tda/dT用下式计算。

对于单一组分：

对于混合物：

6 Benedict-Webb-Rubin-Starling（BWRS）状态方程

6.1 方程的形式及混合规则

1972年Starling和Han提出了BWRS方程，该方程是修正BWR方程而得到的，它保留了BWR方程中与密度关联的系数项，改变了与温度关联的系数项。BWRS方程包含了计算轻烃组分的系数，决定烃类混合物气体系数的混合规则，可以用于热力学性质计算和气液平衡计算。

BWRS状态方程是一个多参数状态方程，其基本形式[10,17]为：

方程中的11 个参数 （A0，B0，C0，D0，E0，a，b，c，d，α，γ） 可以通过参考文献[10]得到。

6.2 焦耳-汤姆逊系数

将式（29） ～（30） 代入式（5） 即可得到焦耳-汤姆逊系数计算公式。

7 L ee-Kesler-Plocker（L KP）状态方程

7.1 方程的形式及混合规则

1978年Plocker等人在Lee-Kesler（LK） 状态方程[18]基础上提出了Lee-Kesler-Plocker（LKP）状态方程[19]，将该方程推广到小分子（如N2、CO、CH4和H2）和大分子（如高沸点的烷烃、芳烃和稠环化合物）组成的不对称混合物的气液平衡和焓的计算中，保留了LK方程的原型，修改了混合规则，增加了两个参数kij和η，其中二元交互系数kij可由纯组分的临界参数关联得到；虚拟临界温度混合规则中的通用指数η为：对称混合物η=0，稍稍不对称混合物η=1，严重不对称混合物η=0.25。kij和η的引入提高了方程的精确度。LKP方程及其混合规则如下：

式中：Z为压缩因子，ω为偏心因子，pr为对比压力，Vr为对比摩尔体积，上标（0） 表示简单流体的相应参数，上标（r）表示参考流体的相应参数，其余参数为常数。

对于混合物，虚拟临界性质表达式[19]：

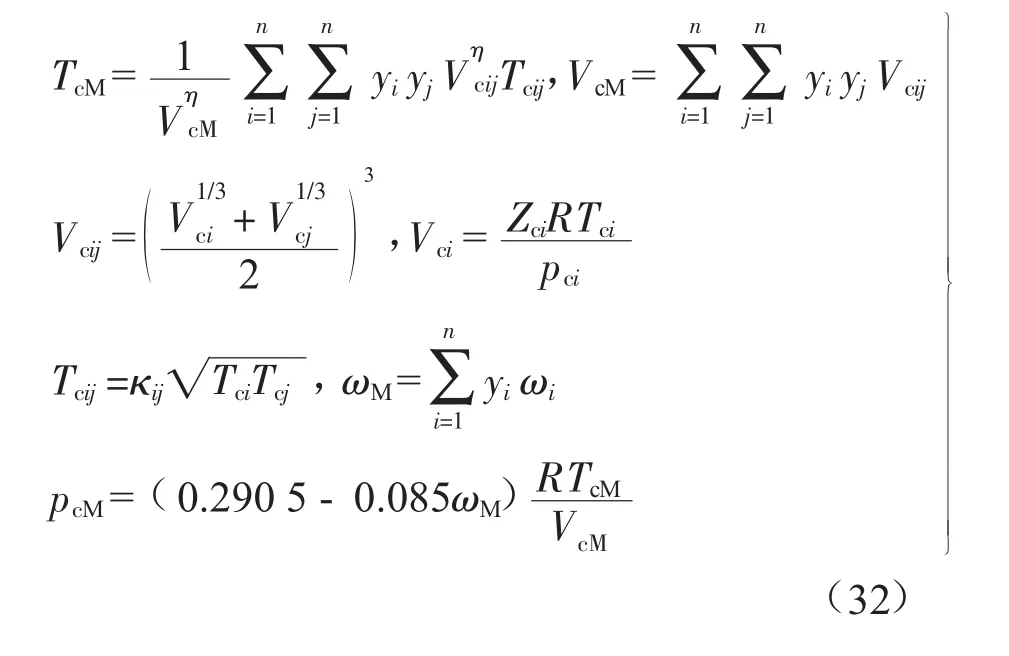
式中：M代表混合物；η取值0.25。

7.2 焦耳-汤姆逊系数

将式 （33） ～（34） 代入式 （4） 可得到

LKP方程求解简单流体和参考流体的焦耳-汤姆逊系数，代入式（35）得到流体的焦耳-汤姆逊系数。

8 结论

（1） 使用RK、SRK、PR、BWRS和LKP状态方程对流体的焦耳-汤姆逊公式进行了推导，给出了焦耳-汤姆逊公式。

（2）由于大多数文献没有温度导数的相关公式，对SRK、PR方程的温度一阶导数进行了推导，给出了单一流体和混合物的表达式。

（3）将立方方程、多参数方程和对比态原理方程具有代表性的状态方程进行归纳讨论，便于设计、科研人员使用和进一步研究。